基于微分求積法分析粘彈性樁基的混沌效應(yīng)
張繼松 琚宏昌


摘 要:為了更好地研究預(yù)制基礎(chǔ)樁的非線(xiàn)性動(dòng)力特征及其它特性,考慮樁-土之間的摩擦影響,利用kelvin模型,建立在軸向荷載下粘彈性樁基的非線(xiàn)性振動(dòng)動(dòng)力學(xué)模型,通過(guò)力學(xué)模型分析得到結(jié)構(gòu)的動(dòng)力偏微分方程;運(yùn)用微分求積法(DQM)將偏微分方程在空間域進(jìn)行網(wǎng)格劃分并離散化,進(jìn)而導(dǎo)出粘彈性樁基的常微分動(dòng)力方程;最后用matlab數(shù)值模擬得到不同樁基彈性模量下的相平面圖、功率譜圖、龐加萊截面圖和時(shí)程曲線(xiàn)圖.結(jié)果表明:在軸向荷載作用下粘彈性樁基會(huì)發(fā)生混沌運(yùn)動(dòng),且樁基彈性模量越大樁基越容易發(fā)生混沌運(yùn)動(dòng),同時(shí)更加直觀形象地驗(yàn)證了混沌效應(yīng)的基本特征.
關(guān)鍵詞:粘彈性樁;kelvin模型;微分求積法;混沌
中圖分類(lèi)號(hào):TU311.3 文獻(xiàn)標(biāo)志碼:A
0 引言
隨著科技的發(fā)展,大量新型材料被廣泛運(yùn)用到實(shí)際工程中,使得傳統(tǒng)結(jié)構(gòu)呈現(xiàn)出粘彈性的性能,并引起了大量的學(xué)者對(duì)其進(jìn)行研究.樁基作為工程中常見(jiàn)的結(jié)構(gòu),建立其非線(xiàn)性動(dòng)力學(xué)模型對(duì)研究樁的動(dòng)力學(xué)分析有重要的意義.胡春林等[1-2]研究非線(xiàn)性粘彈性嵌巖樁縱向振動(dòng)中運(yùn)用Galerkin方法將非線(xiàn)性偏微分方程進(jìn)行簡(jiǎn)化得到簡(jiǎn)化的偏微分-積分動(dòng)力學(xué)方程.劉明等[3]分析樁基軸向振動(dòng)動(dòng)力學(xué)時(shí)運(yùn)用多時(shí)間尺度法對(duì)動(dòng)力學(xué)偏微分方程進(jìn)行近似簡(jiǎn)化.駱文和等[4]運(yùn)用分離變量法對(duì)動(dòng)力學(xué)方程簡(jiǎn)化分析了樁-土之間的豎向振動(dòng).隨后,學(xué)者運(yùn)用復(fù)模態(tài)法[5]、分?jǐn)?shù)導(dǎo)數(shù)微分[6]等方法研究分析了樁基非線(xiàn)性動(dòng)力學(xué)振動(dòng).
為了更好地分析樁基的非線(xiàn)性動(dòng)力學(xué)行為,如何建立粘彈性樁的動(dòng)力學(xué)方程就顯得尤為重要.本文采用微分求積法[7-9]對(duì)粘彈性樁基的動(dòng)力學(xué)偏微分方程在空間域進(jìn)行網(wǎng)格劃分離散簡(jiǎn)化,得到粘彈性預(yù)制基礎(chǔ)樁基的非線(xiàn)性動(dòng)力學(xué)常微分方程模型,最后采用四階Runge-Kutta法運(yùn)用matlab數(shù)值模擬分析樁基在軸向荷載下發(fā)生的復(fù)雜的非線(xiàn)性動(dòng)力學(xué)行為.
1 力學(xué)模型的建立
一個(gè)等截面圓形基礎(chǔ)樁.設(shè)樁長(zhǎng)為l,直徑為d,截面面積為A.材料的密度為ρ,樁在軸向荷載的作用下,截面始終保持為平面.假定樁基向上為正半軸,樁基底部的圓心為坐標(biāo)系的原點(diǎn)處,如圖1所示.考慮樁-土之間的相互作用力,假定周?chē)翆?duì)樁基的反力大小與位移成正比,且周?chē)翆?duì)樁身的阻力大小與其位移速率也成正比,則預(yù)制基礎(chǔ)樁的動(dòng)力學(xué)模型為:
3 數(shù)值模擬
采用四階Runge-Kutta法對(duì)非線(xiàn)性常微分動(dòng)力學(xué)模型運(yùn)用matlab數(shù)值模擬分析.初始參數(shù)為樁的直徑A=0.1 m2,材料的密度ρ=2.5 g/cm3,土的剛度系數(shù)k=2.2×105 Pa,阻尼系數(shù)C=2.3×103 Pa·s,樁身的粘彈性系數(shù)?濁=1×105 Pa·s.外部軸向荷載作用力為F=500 N.
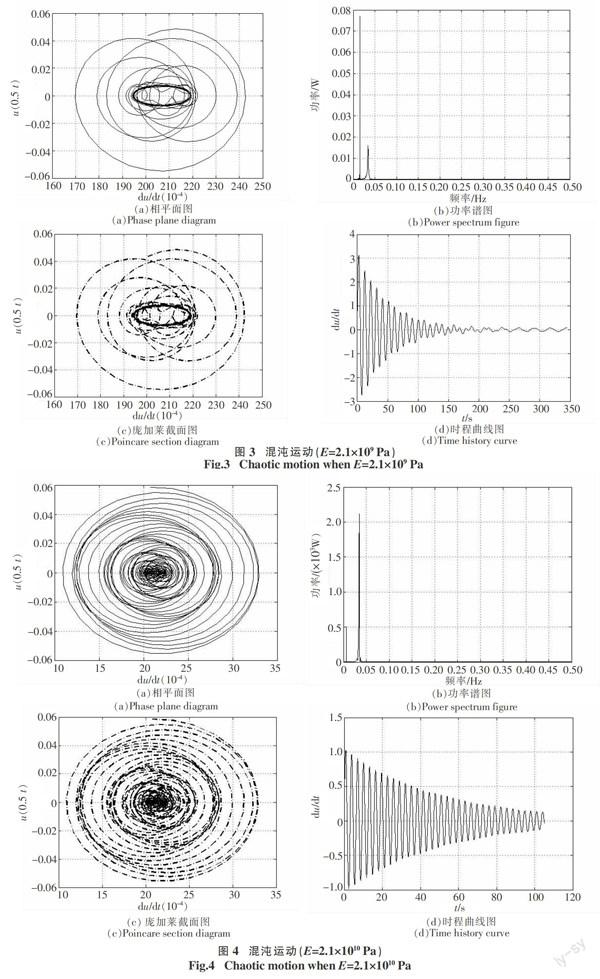
假設(shè)材料彈性模量E的變化范圍為2.1×108 Pa~2.1×1010 Pa,以步長(zhǎng)為10增加,進(jìn)而得到3組所對(duì)應(yīng)的相平面圖、功率譜圖、龐加萊截面圖、時(shí)程曲線(xiàn)圖,如圖2~圖4所示.
分別對(duì)比分析圖2~圖4中所對(duì)應(yīng)的相平面圖、功率譜圖、龐加萊截面圖、時(shí)程曲線(xiàn)圖,可發(fā)現(xiàn)隨著樁基彈性模量的增加, 樁基將從周期運(yùn)動(dòng)進(jìn)入混沌運(yùn)動(dòng), 彈性模量越大越容易發(fā)生混沌運(yùn)動(dòng), 同時(shí)圖3和圖4也符合混沌效應(yīng)的基本特征,具體分析如下:
1)對(duì)于相平面圖分析,圖2中的相平面圖形中明顯是個(gè)封閉的運(yùn)動(dòng)軌線(xiàn),圖3和圖4的圖形中明顯扭結(jié)在一起形成一個(gè)不封閉的運(yùn)動(dòng)軌跡,具有無(wú)限層次的自相似性;
2)對(duì)于功率譜圖分析,圖2中功率譜圖中對(duì)應(yīng)尖峰,而圖3和圖4中圖形出現(xiàn)“噪聲背景”和寬峰;
3)對(duì)于龐加萊截面圖分析,圖2中的龐加萊截面圖上是個(gè)閉合的曲線(xiàn)圖形,而圖3和圖4中的圖形漸漸呈現(xiàn)出成片的密集點(diǎn),越來(lái)越具有層次結(jié)構(gòu)性;
4)對(duì)于時(shí)程曲線(xiàn)圖分析,圖2中時(shí)程曲線(xiàn)圖在一段時(shí)間后出現(xiàn)了一定的規(guī)律,沒(méi)有了跳動(dòng)性變化,非常穩(wěn)定,而圖3和圖4中的功率譜圖形隨著時(shí)間的推移,一直有跳躍性變動(dòng).
4 結(jié)論
本文考慮了樁-土之間摩擦影響,建立了在軸向荷載下粘彈性預(yù)制基礎(chǔ)樁的動(dòng)力學(xué)偏微分運(yùn)動(dòng)學(xué)方程.利用微分求積法在空間域進(jìn)行網(wǎng)格劃分離散對(duì)其簡(jiǎn)化得到常微分方程,這種方法更加簡(jiǎn)潔,在matlab的分析中更為準(zhǔn)確.數(shù)值分析表明:受軸向荷載作用下的粘彈性樁基可以呈現(xiàn)出周期運(yùn)動(dòng)和混沌運(yùn)動(dòng);樁身彈性模量對(duì)樁基的混沌運(yùn)動(dòng)有影響,彈性模量越大樁基越容易發(fā)生混沌運(yùn)動(dòng);同時(shí)圖形也更加直觀形象地反映出了混沌運(yùn)動(dòng)的基本特征.
參考文獻(xiàn)
[1] 胡春林,程昌鈞.非線(xiàn)性粘彈性基樁縱向混沌運(yùn)動(dòng)[J].巖土力學(xué),2005,26(10):1541-1544.
[2] 任九生,程昌鈞.非線(xiàn)性粘彈性樁耦合運(yùn)動(dòng)中的混沌分析[J].振動(dòng)與沖擊, 2006, 25(5):21-23,189.
[3] 劉民,陳中學(xué),胡春林.基于多時(shí)間尺度法的樁基軸向振動(dòng)分析研究[J].長(zhǎng)江科學(xué)院院報(bào), 2009,26(12):102-105.
[4] 駱文和,閆啟方.考慮樁-土相互作用的粘彈性土中管樁的縱向動(dòng)力阻抗分析[J].昆明理工大學(xué)學(xué)報(bào)(理工版),2010, 35(5):28-32,36.
[5] 劉民,陳中學(xué).基于復(fù)模態(tài)法的粘彈性基樁橫向振動(dòng)研究[J].長(zhǎng)江科學(xué)院院報(bào),2010,27(12):76-78,82.
[6] 劉林超, 閆啟方,楊驍.分?jǐn)?shù)導(dǎo)數(shù)粘彈性土層模型中樁基豎向振動(dòng)特性研究[J].工程力學(xué),2011,28(8):177-182.
[7] 劉靜,朱媛媛,胡育佳.基礎(chǔ)-飽和土地基耦合系統(tǒng)分析的微分求積單元法[J].力學(xué)季刊,2014,35(1):54-65.
[8] 陳姍,琚宏昌.簡(jiǎn)諧荷載作用下粘彈性梁振動(dòng)的非線(xiàn)性動(dòng)力學(xué)模型及其簡(jiǎn)化[J].廣西科技大學(xué)學(xué)報(bào),2014, 25(4):30-33,39.
[9] 王冬梅,張偉,李慕榮.用微分求積法分析軸向移動(dòng)粘彈性梁的非平面非線(xiàn)性振動(dòng)[J].動(dòng)力學(xué)與控制學(xué)報(bào), 2015,13(1):23-27.
Abstract: To study the nonlinear dynamic characteristics and other characteristics of prefabricated foundation piles better, considering the influence of friction between pile and soil and based on the Kelvin model, nonlinear vibration dynamic model of viscoelastic pile under axial load is established. The dynamic partial differential equation of structure is obtained by the analysis of the mechanical model, the partial differential equations are partitioned and discretized in space domain by differential quadrature method (DQM), and the ordinary differential dynamic equations of viscoelastic foundation pile are derived. Finally, phase diagram, power spectrum, poincare section and time history curve are gained with numerical simulation of matlab. The results show that the chaotic motion can occur in the viscoelastic foundation pile under axial load; the bigger the elastic modulus of pile foundation, the more prone to chaotic motion; meanwhile, the basic features of chaotic effects are more intuitively and vividly verified.
Key words: viscoelastic foundation pile; Kelvin model; differential quadrature method; chaos
(學(xué)科編輯:黎 婭)

