模糊規(guī)則相似性計(jì)算與性能分析研究
李微,喬俊飛,韓紅桂,曾曉軍
(1.北京工業(yè)大學(xué) 信息學(xué)部,北京 100124; 2. 計(jì)算智能與智能系統(tǒng)北京市重點(diǎn)實(shí)驗(yàn)室,北京 100124; 3. 曼徹斯特大學(xué) 計(jì)算機(jī)科學(xué)學(xué)院,曼徹斯特 M13 9PL)
模糊規(guī)則相似性計(jì)算與性能分析研究
李微,喬俊飛,韓紅桂,曾曉軍
(1.北京工業(yè)大學(xué) 信息學(xué)部,北京 100124; 2. 計(jì)算智能與智能系統(tǒng)北京市重點(diǎn)實(shí)驗(yàn)室,北京 100124; 3. 曼徹斯特大學(xué) 計(jì)算機(jī)科學(xué)學(xué)院,曼徹斯特 M13 9PL)
針對模糊規(guī)則相似性分析和計(jì)算問題,本文對模糊規(guī)則相似性計(jì)算方法進(jìn)行了研究。首先,將模糊規(guī)則相似性等價(jià)地轉(zhuǎn)化為多變量模糊集相似性,并對模糊規(guī)則相似性計(jì)算方法提出3種應(yīng)用性能評價(jià)指標(biāo)——可區(qū)分性、維數(shù)依賴性和計(jì)算復(fù)雜性。其次,在現(xiàn)有兩種模糊規(guī)則相似性計(jì)算方法的基礎(chǔ)上,提出4種新的計(jì)算方法,對各種方法進(jìn)行系統(tǒng)地性能分析和比較。最后,對模糊規(guī)則相似性計(jì)算進(jìn)行仿真研究,結(jié)果表明了所提應(yīng)用性能指標(biāo)的有效性、計(jì)算方法的可行性及分析結(jié)果的正確性。本文研究結(jié)果為模糊規(guī)則相似性分析和計(jì)算提供了依據(jù), 尤其為基于模糊規(guī)則相似性辨識和合并的模糊系統(tǒng)與模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡化奠定了基礎(chǔ),提供了一種新的設(shè)計(jì)思路。
模糊規(guī)則;相似性計(jì)算;可區(qū)分性;維度依賴性;計(jì)算復(fù)雜性
自從Zadeh教授于1965年創(chuàng)立模糊集理論[1]以來,以模糊集為基礎(chǔ)的模糊系統(tǒng)在自動控制、信息處理等領(lǐng)域得到了廣泛應(yīng)用[2-4]。模糊集相似性分析是模糊系統(tǒng)研究的一個(gè)重要分支,得到眾多學(xué)者的關(guān)注,在系統(tǒng)辨識與結(jié)構(gòu)簡化[5-15]、模式識別[16-17]、模糊聚類[18]等方面取得了豐碩的研究成果。
在模糊系統(tǒng)或模糊神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)過程中,不但要計(jì)算模糊集相似性,而且要計(jì)算模糊規(guī)則相似性,以合并相似規(guī)則,進(jìn)而獲得簡潔的網(wǎng)絡(luò)結(jié)構(gòu),降低模型的復(fù)雜度。因此,模糊規(guī)則相似性分析與計(jì)算是模糊系統(tǒng)或模糊神經(jīng)網(wǎng)絡(luò)研究領(lǐng)域的關(guān)鍵問題之一。
目前,針對模糊規(guī)則相似性分析與計(jì)算的研究工作不多。Chao等[5]提出最小值模糊規(guī)則相似度計(jì)算方法,該方法通過計(jì)算每個(gè)輸入變量隸屬函數(shù)的相似度,將所有變量相似度的最小值作為模糊規(guī)則的相似度。Chen等[6]、Tsekouras[7]都采用該方法對模糊規(guī)則相似性進(jìn)行計(jì)算。然而,在理論方面,該方法與常用的相似度定義不一致;在應(yīng)用方面,該方法不能很好地區(qū)分模糊規(guī)則的相似性。
模糊規(guī)則相似性研究通常只考慮滿足模糊集相似性的基本數(shù)學(xué)準(zhǔn)則,而在模糊神經(jīng)網(wǎng)絡(luò)簡化結(jié)構(gòu)中,模糊規(guī)則相似性計(jì)算僅僅滿足基本數(shù)學(xué)準(zhǔn)則不足以滿足應(yīng)用的要求。
鑒于上述問題,文中提出4種模糊規(guī)則相似性計(jì)算方法,通過歸納應(yīng)用中對模糊規(guī)則相似性的要求,提出3種應(yīng)用性能評價(jià)指標(biāo)——可區(qū)分性、維數(shù)依賴性和計(jì)算復(fù)雜性,并以此為基礎(chǔ),對各種相似性計(jì)算方法進(jìn)行詳細(xì)分析和比較。研究結(jié)果為模糊規(guī)則相似性分析及應(yīng)用提供了依據(jù)。
1 模糊規(guī)則相似性計(jì)算問題描述
1.1 問題描述
討論模糊規(guī)則相似性計(jì)算問題之前,首先給出常用的模糊集相似性定義[5,8]。
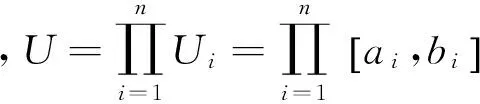
式中:S(A,B)表示A和B的相似度;M(A∩B)表示A和B交集的面積;M(A∪B)表示A和B并集的面積。
在模糊規(guī)則相似性計(jì)算問題中,假設(shè)一對模糊規(guī)則RA和RB表述如下。
RA:如果x1是A1,…,xn是An,那么y是wA(x)
(2)
RB:如果x1是B1,…,xn是Bn,那么y是wB(x)
(3)
式中:xi∈Ui?R是第i個(gè)輸入變量;Ui是其相應(yīng)輸入變量空間;Ai和Bi是關(guān)于輸入變量xi的模糊集,其相應(yīng)隸屬函數(shù)分別為uAi(xi)和uBi(xi),i=1,2,…,n;x=(x1,…,xn),n為輸入變量個(gè)數(shù);wA(x)和wB(x)是模糊規(guī)則的結(jié)論。當(dāng)給定一個(gè)Mamdani型系統(tǒng)或網(wǎng)絡(luò)時(shí),wA(x)=CA;當(dāng)給定一個(gè)T-S型時(shí),wA(x)=CA0+CA1x1+…+CAnxn,其中Cj(j=A,A0,…,An)為常數(shù)。
由于一對模糊規(guī)則涉及兩組模糊集,無法直接應(yīng)用定義1給出的模糊集相似性計(jì)算模糊規(guī)則的相似性。因此,引入多變量模糊集對上述規(guī)則RA和RB重新表述如下。
RA:如果x是A,那么y是wA(x)
(4)
RB:如果x是B,那么y是wB(x)
(5)
式中:A和B為輸入空間U上兩個(gè)多變量模糊集;A=A1×A2×…×An,B=B1×B2×…×Bn,相應(yīng)規(guī)則的激活強(qiáng)度分別為
模糊規(guī)則RA和RB的相似性定義為,在輸入空間U上兩個(gè)多變量模糊集A和B的相似性。
因此,通過引用多變量模糊集的概念,將兩條模糊規(guī)則的相似性等價(jià)地轉(zhuǎn)換成兩個(gè)多變量模糊集的相似性,而如何計(jì)算模糊規(guī)則RA和RB的相似度S(A,B)是需要解決的問題。
1.2 性能評價(jià)指標(biāo)
由于模糊規(guī)則相似性等價(jià)于多變量模糊集相似性,因此也必須滿足模糊集相似性的基本數(shù)學(xué)準(zhǔn)則[8-9],歸納如下。
模糊規(guī)則相似性S(A,B)的基本數(shù)學(xué)準(zhǔn)則如下。
1) 正則性:0≤S(A,B)≤1。
2) 對稱性:S(A,B)=S(B,A)。
3) 不相交模糊規(guī)則的相似度應(yīng)為0,即
S(A,B)=0?uA(x)uB(x)=0,?x∈U。
4)相交模糊規(guī)則的相似度應(yīng)大于0,即
S(A,B)>0??x∈U,uA(x)uB(x)>0。
當(dāng)相似度為1時(shí),兩條模糊規(guī)則是完全相同的,即
S(A,B)=1?uA(x)=uB(x),?x∈U
5) 縮放或移位下的不變性,即
S(A′,B′)=S(A,B)?uA′(l+kx)=uA(x),
uB′(l+kx)=uB(x),l∈Rn,k∈R,k>0。
然而,將模糊規(guī)則相似性計(jì)算方法應(yīng)用于模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡化時(shí),不但要滿足基本數(shù)學(xué)準(zhǔn)則,而且要滿足實(shí)際應(yīng)用的要求。為此,提出以下3種評價(jià)指標(biāo)。
1.2.1 可區(qū)分性
可區(qū)分性是指對兩個(gè)明顯不同模糊規(guī)則,其相應(yīng)相似度能夠反映出模糊規(guī)則的不同。可區(qū)分性可被看作相似度定義的靈敏度性能指標(biāo),區(qū)分性好的相似度具有較高的靈敏度。該指標(biāo)能夠更好地辨識出相似度高或低的模糊規(guī)則。
1.2.2 維數(shù)依賴性
維數(shù)依賴性是指模糊規(guī)則相似度值是否會隨著維數(shù)的增加或減少而變化。維數(shù)依賴性是模糊規(guī)則相似度辨識與合并中非常重要的性能指標(biāo)。如果相似度的定義具有維數(shù)依賴性,對每個(gè)不同維數(shù)的系統(tǒng)辨識需要大量數(shù)據(jù)和實(shí)驗(yàn)才能確定合適的相似度閾值,給實(shí)際應(yīng)用帶來一定困難;如果相似度計(jì)算不依賴系統(tǒng)維數(shù)的變化而變化,可確定一個(gè)通用的相似度閾值,用于各種不同維數(shù)的模糊系統(tǒng)或網(wǎng)絡(luò)進(jìn)行結(jié)構(gòu)簡化。
1.2.3 計(jì)算復(fù)雜性
計(jì)算復(fù)雜性是指計(jì)算模糊規(guī)則相似度所需的步驟和時(shí)間。如果模糊規(guī)則相似度計(jì)算過于復(fù)雜,會影響計(jì)算的有效性,限制算法的可用性。
2 計(jì)算方法與性能分析
2.1 最小值方法
最小值方法[5-7]將所有輸入變量xi(i=1,2,…,n)相應(yīng)模糊集相似度的最小值作為模糊規(guī)則的相似度,其計(jì)算公式如下:
首先,可證明基于最小值的模糊規(guī)則相似度計(jì)算方法滿足相似性的基本數(shù)學(xué)準(zhǔn)則;其次,計(jì)算簡單,當(dāng)?shù)玫矫總€(gè)輸入變量相應(yīng)單變量模糊集的相似度S(Ai,Bi)后,取最小值運(yùn)算即可得到模糊規(guī)則的相似度;最后,該方法取值僅取決于某個(gè)輸入變量相應(yīng)模糊集的相似度,不具有維數(shù)依賴性。
然而,由式(7)可知,該方法與相似度定義(式(1))不一致,且可區(qū)分性較差。例如,有兩條模糊規(guī)則,其相應(yīng)輸入變量xi的模糊集合分別為Ai和Bi(i=1,2,3),考慮以下兩種情況。情況1:每個(gè)變量相應(yīng)模糊集的相似度均相同,即S(Ai,Bi)=0.4,(i=1,2,3),采用最小值方法,這兩條規(guī)則的相似度為S1(A,B)=0.4。情況2:各變量相應(yīng)模糊集的相似度分別為S(A1,B1)=0.4,S(A2,B2)=0.9,S(A3,B3)=0.9,采用最小值方法,這兩條規(guī)則的相似度仍為0.4。結(jié)果顯示,在第2種情況下,兩條模糊規(guī)則的相似度明顯大于第一種情況的相似度。因此,最小值方法不能很好地區(qū)分模糊規(guī)則間的明顯差異,在一定程度上影響相似度的有效判定。
2.2 乘積方法及其改進(jìn)方法
針對最小值方法存在可區(qū)分性差的問題,提出了乘積方法,該方法是對最小值方法的改進(jìn),通過計(jì)算所有輸入變量相應(yīng)模糊集相似度的乘積得到模糊規(guī)則的相似度,即
首先,可證明乘積法滿足相似性的基本數(shù)學(xué)準(zhǔn)則;其次,乘積方法計(jì)算簡單,且可區(qū)分性較好。如上例,采用乘積方法,在兩種情況下,兩條模糊規(guī)則的相似度分別為0.064和0.324。結(jié)果表明,第2種情況比第1種情況下的模糊規(guī)則具有更高的相似度。因此,乘積方法能夠更好地區(qū)分模糊規(guī)則的相似性。
然而,由式(8)可知,乘積方法仍然與相似度定義1不一致,是一種直觀方法。而且,由于相似度取值范圍為[0,1],隨著維度不斷增加,相似度越來越小。如上例,在第1種情況下,每個(gè)單變量模糊集的相似度均為0.4,n維變量模糊規(guī)則相似度為(0.4)n,當(dāng)維數(shù)逐漸增加時(shí),得到的相似度呈現(xiàn)遞減的趨勢。
為了克服乘積法具有維數(shù)依賴性的缺點(diǎn),提出了一種改進(jìn)的方法(第3種方法),即
該方法繼承了乘積方法滿足基本數(shù)學(xué)準(zhǔn)則、計(jì)算簡單和可區(qū)分性好的優(yōu)點(diǎn),克服了維數(shù)依賴性的不足。如上例,當(dāng)每個(gè)變量模糊集的相似度均為0.4時(shí),無論維數(shù)如何增加,模糊規(guī)則的相似度仍為
即相似度不隨維數(shù)的變化而變化。
綜上所述,改進(jìn)的乘積方法是一種比較理想的模糊規(guī)則相似度計(jì)算方法,不足之處在于該方法是一種直觀的方法,不滿足常用的相似度定義。
2.3 交并面積和比值法
根據(jù)模糊集相似度定義[5,8]的直觀意義,兩條模糊規(guī)則總交集的面積可定義為每個(gè)輸入變量相應(yīng)的一對模糊集的交集面積之和。同理,其總并集的面積可定義為每個(gè)輸入變量相應(yīng)的一對模糊集的并集面積之和,從而類似于定義1,模糊規(guī)則相似性定義為交集面積之和與并集面積之和的比值。因此,將該方法(即第4種方法)命名為交并面積和比值法,其計(jì)算公式為
其中



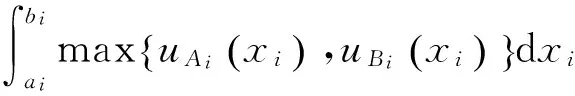
首先,由式(10)~(12)可以證明,該方法滿足相似性的基本數(shù)學(xué)準(zhǔn)則;其次,計(jì)算簡單,當(dāng)?shù)玫矫總€(gè)輸入變量相應(yīng)模糊集的交集與并集面積后,通過簡單的求和與比值運(yùn)算即可得到模糊規(guī)則的相似度。而且,該方法不具有維數(shù)依賴性。例如,在n維空間的兩條模糊規(guī)則,每對單變量模糊集Ai和Bi(i=1,2,…,n)的交集面積為0.4,并集面積為0.8,則當(dāng)n=1時(shí),這兩條規(guī)則的相似度為0.5;當(dāng)n>1時(shí),相似度為
即隨著輸入空間維數(shù)的變化,模糊規(guī)則相似度不會隨之變化。
此外,該方法具有很好的可區(qū)分性。例如,一對兩維模糊規(guī)則的單變量交集與并集面積分別為
M(A1∩B1)=M(A2∩B2)=0.4
M(A1∪B1)=M(A2∪B2)=0.8
則根據(jù)式(10)得到這對模糊規(guī)則的相似度為0.5。假定另一對模糊規(guī)則的單變量交集與并集面積分別為
M(A1∩B1)=0.4,M(A1∪B1)=0.8
M(A2∩B2)=0.35,M(A2∪B2)=0.8
則相似度為0.47。因此,該方法能夠很好地區(qū)分模糊規(guī)則的相似性。
綜上所述,交并面積和比值法是一種較理想、具有很好直觀意義的模糊規(guī)則相似度計(jì)算方法,而且在一定程度上接近于常用的相似度定義。
2.4 交并總面積比值法及其改進(jìn)方法
第5種方法是作者前期提出的交并總面積比值法,其相似度計(jì)算公式如下[19]:
式中

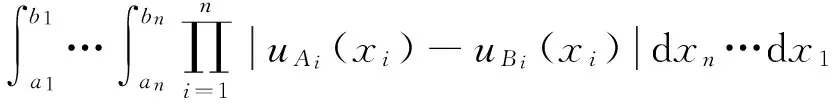
首先,由式(13)~(16)可知,該方法與相似度定義一致;其次,該方法滿足相似性的基本數(shù)學(xué)準(zhǔn)則(證明過程見附錄)。而且,由于模糊規(guī)則或多變量模糊集A和B之間的任何不同之處都可通過M(|A~B|)體現(xiàn),導(dǎo)致式(13)定義的S(A,B)不同。因此,該方法具有很好的可區(qū)分性。
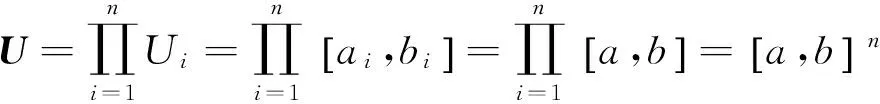
式中:c為兩個(gè)高斯函數(shù)的中心;σA和σB分別為兩個(gè)高斯函數(shù)的寬度,且σA>σB>0。于是,
M(|A~B|)如式(16)所示。由于σA>σB>0,推出
因此得出
代入式(13)得到:
由式(21)得出:
因此,由式(23)可推出,當(dāng)n→時(shí),
即無論Ai和Bi多相似,只要它們不相同(即相似度小于1),當(dāng)輸入空間維數(shù)逐漸增加時(shí),A和B的相似度會逐漸減小;當(dāng)輸入空間維數(shù)趨于無窮時(shí),相似度趨于0。
為了克服維數(shù)依賴性的缺點(diǎn),提出一種改進(jìn)的交并總面積比值法(即第6種方法),如下式所示:
該方法滿足相似性基本數(shù)學(xué)準(zhǔn)則,具有很好的可區(qū)分性,且不具有維數(shù)依賴性。如上例,采用該方法計(jì)算式(23)可得到:
因此,得到的相似度不隨維數(shù)的變化而變化。
需要指出的是,改進(jìn)的交并總面積比值法仍存在計(jì)算復(fù)雜的缺點(diǎn)。同時(shí),該方法不再滿足常用的相似性定義。
2.5 6種方法的性能比較
上述分析和比較結(jié)果顯示,6種方法都滿足相似性定義的基本數(shù)學(xué)準(zhǔn)則。在應(yīng)用性能指標(biāo)方面,每種方法各有不同。表1給出了這6種方法在3個(gè)性能指標(biāo)方面的比較結(jié)果。

表1 6種方法的性能對比
由表1可知,改進(jìn)的乘積方法與交并面積和比值法是兩種比較理想的模糊規(guī)則相似性計(jì)算方法。
3 仿真實(shí)驗(yàn)
本文所做的實(shí)驗(yàn)研究均是基于Matlab R2014a在Intel?CoreTM2 Duo CPU 3 GHz,內(nèi)存2 GB的普通PC機(jī)上進(jìn)行的。
3.1 實(shí)驗(yàn)1
假設(shè)有3個(gè)輸入變量(x1,x2,x3)、6條模糊規(guī)則(R1,R2,R3,R4,R5,R6),高斯函數(shù)中心(c)和寬度(σ)如表2所示。分別采用最小值法、乘積法、改進(jìn)乘積法、交并面積和比值法、改進(jìn)交并面積和比值法、交并總面積比值法及改進(jìn)交并總面積比值法共6種方法對模糊規(guī)則相似性進(jìn)行計(jì)算,其中單變量相似性計(jì)算方法采用文獻(xiàn)[20]提出的方法。得到的相似度及相應(yīng)的運(yùn)行時(shí)間如表3所示,采用最小值方法得到部分規(guī)則相似度如表4所示,其中,Sij代表第i和第j條規(guī)則的相似度,M1~M6依次代表上述6種相似性計(jì)算方法。

表2 中心和寬度值

表3 6種方法相似度及運(yùn)行時(shí)間
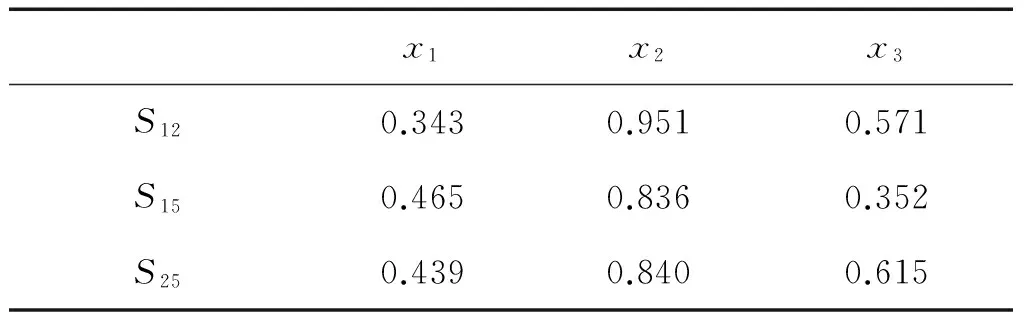
表4 最小值方法相似度
從3個(gè)應(yīng)用性能指標(biāo)方面對實(shí)驗(yàn)結(jié)果進(jìn)行進(jìn)一步分析。
3.1.1 可區(qū)分性
由表2可知,對變量x1而言,在規(guī)則R1中其值近似于2.547 6 (即其中心),而在R2和R5中,其值近似于3.821 2和3.541 6。因此,與R1最不相似的是R2和R5。對于變量x2和x3而言,相比R1與R5,R1與R2則較為相似。然而,由表3及表4可知,對最小值方法而言,相似度S12和S15完全取決于在各個(gè)變量中最不相似模糊集的相似度,即0.343與0.352,如表3所示,最小值方法得到的S12和S15較為接近,其余5種方法得到的S12和S15均呈現(xiàn)出差異。因此,該實(shí)驗(yàn)表明最小值法的可區(qū)分性較差,而另5種方法在一定程度上克服了這一缺點(diǎn)。
3.1.2 維數(shù)依賴性
由表3可知,方法M2和M5所得到的模糊規(guī)則相似度都小于0.5。通常相似度大于0.5才能進(jìn)行規(guī)則合并。如果采用方法M2或M5,則沒有一對規(guī)則需要進(jìn)行合并,而通過相應(yīng)的改進(jìn)方法M3或M6,該缺陷得到了明顯的改善,多對模糊規(guī)則都顯示出很好的相似性。
此外,對任何一對模糊規(guī)則,方法M2的相似度都小于方法M5的相似度,因此,方法M2比M5維數(shù)依賴性更強(qiáng)。
3.1.3 計(jì)算復(fù)雜性
表3顯示,方法M1、M2、M3和M4的運(yùn)行時(shí)間短,計(jì)算簡單,而方法M5與M6則較復(fù)雜。對于一個(gè)三維輸入、6條規(guī)則的模糊神經(jīng)網(wǎng)絡(luò),方法M5與M6的計(jì)算時(shí)間是方法M1、M2、M3和M4的4 000多倍。對于更加高維和具有更多規(guī)則的模糊系統(tǒng)或模糊神經(jīng)網(wǎng)絡(luò),計(jì)算時(shí)間會更長。因此,方法M5與M6不適用于高維復(fù)雜系統(tǒng)的結(jié)構(gòu)簡化。
實(shí)驗(yàn)結(jié)果表明,改進(jìn)的乘積方法與交并面積和比值法是較理想的模糊規(guī)則相似性計(jì)算方法。
3.2 實(shí)驗(yàn)2
假設(shè)有4個(gè)輸入變量(x1,x2,x3,x4)、一對模糊規(guī)則(R1,R2),高斯函數(shù)中心(c)和寬度(σ)如表5所示。與實(shí)驗(yàn)1類似,分別采用最小值法等六種方法對模糊規(guī)則相似性進(jìn)行計(jì)算,得到的相似度及相應(yīng)的運(yùn)行時(shí)間如表6所示,其中,S12代表兩條規(guī)則的相似度,M1、M2、M3、M4、M5和M6依次代表6種相似性計(jì)算方法。

表5 中心和寬度
表6 6種方法相似度及運(yùn)行時(shí)間
Table 6 Similarity degree and running time of six methods

S12時(shí)間/sM10.0660.036M20.0150.037M30.3520.038M40.4630.038M50.0671359.807M60.5081366.569
由表6可知,與方法M3、M4和M6相比,方法M2與M5得到的模糊規(guī)則相似度小很多,表明這兩種方法具有維數(shù)依賴性。在運(yùn)行時(shí)間方面,相比前4種方法,方法M5與M6計(jì)算較為復(fù)雜。因此,實(shí)驗(yàn)結(jié)果進(jìn)一步表明,改進(jìn)的乘積方法與交并面積和比值法不具有維數(shù)依賴性,計(jì)算較為簡單,是較理想的模糊規(guī)則相似性計(jì)算方法。
3.3 實(shí)驗(yàn)3
該實(shí)驗(yàn)以三角形隸屬函數(shù)為例。假設(shè)有3個(gè)輸入變量(x1,x2,x3),一對模糊規(guī)則(R1,R2),三角形函數(shù)的參數(shù)包括下部左頂點(diǎn)(p1)、上部頂點(diǎn)(q)和下部右頂點(diǎn)(p2)值如表7所示。與實(shí)驗(yàn)1和實(shí)驗(yàn)2類似,采用最小值法等6種方法計(jì)算得到的規(guī)則相似度及相應(yīng)的運(yùn)行時(shí)間如表8所示。

表7 三角形函數(shù)的參數(shù)
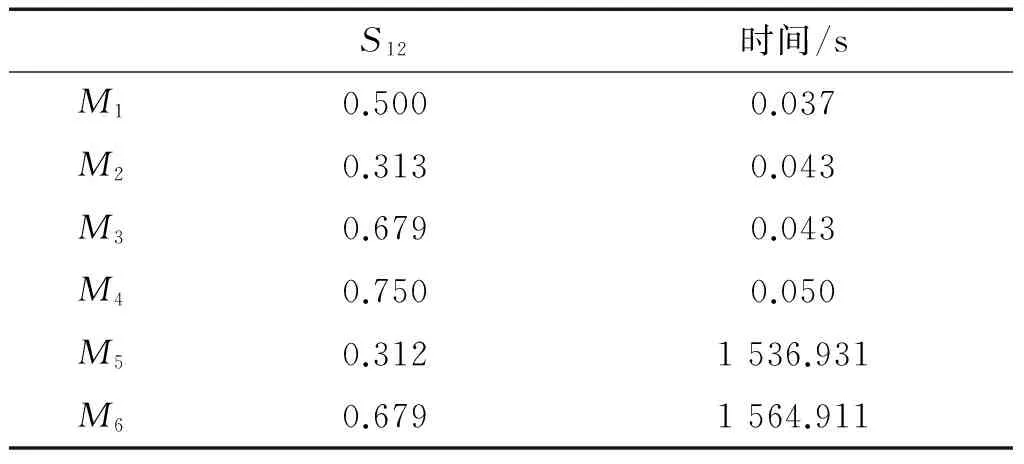
表8 六種方法相似度及相應(yīng)的運(yùn)行時(shí)間
由實(shí)驗(yàn)結(jié)果可知,6種模糊規(guī)則相似性計(jì)算方法不但適用于高斯隸屬函數(shù),而且適用于三角形隸屬函數(shù),具有很好的通用性。在維數(shù)依賴性方面,方法M2與M5得到的模糊規(guī)則相似度較小,表明這兩種方法具有維數(shù)依賴性。在運(yùn)行時(shí)間上,方法M5與M6計(jì)算較為復(fù)雜。
因此,實(shí)驗(yàn)結(jié)果進(jìn)一步表明,改進(jìn)的乘積方法與交并面積和比值法不具有維數(shù)依賴性,計(jì)算簡單,是較理想的模糊規(guī)則相似性計(jì)算方法。而且,基于文中分析與討論,交并面積和比值法具有更好的直觀性,更接近常用的相似度定義。
4 結(jié)束語
本文對模糊規(guī)則相似性計(jì)算進(jìn)行了研究。首先,證明了模糊規(guī)則相似性等價(jià)于多變量模糊集的相似性,并提出了3種應(yīng)用性能評價(jià)指標(biāo)——可區(qū)分性、維數(shù)依賴性和計(jì)算復(fù)雜性。其次,在現(xiàn)有兩種模糊規(guī)則相似性計(jì)算方法的基礎(chǔ)上,提出了4種相似性計(jì)算方法,進(jìn)行了詳細(xì)分析和比較。分析和比較結(jié)果表明,提出的交并面積和比值法,可區(qū)分性好,不具有維數(shù)依賴性,計(jì)算簡單、直觀,是一種比較理想的模糊規(guī)則相似性計(jì)算方法。最后,為更好地說明最小值法等六種方法的優(yōu)缺點(diǎn),給出了數(shù)值分析實(shí)例,并對實(shí)驗(yàn)結(jié)果進(jìn)一步分析。
文中的研究具有以下幾方面意義:1)證明了模糊規(guī)則相似性等價(jià)于多變量模糊集相似性;2)證明了常用的模糊集相似性定義在應(yīng)用于模糊規(guī)則相似性計(jì)算中也存在不足之處,證實(shí)了對模糊規(guī)則相似性進(jìn)一步研究的必要性;3)研究結(jié)果為模糊規(guī)則相似性分析和計(jì)算方法選取提供了依據(jù),尤其是為基于模糊規(guī)則相似性分析與合并的模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡化提供了方法基礎(chǔ)和設(shè)計(jì)思路。
為了有效改善目前模糊規(guī)則相似性在計(jì)算有效性和精確性方面的不足,將提出的各種方法應(yīng)用于模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡化是下一步要進(jìn)行的研究工作。
附錄
交并總面積比值法滿足相似性基本數(shù)學(xué)準(zhǔn)則的定理如下。
定理 假設(shè)多變量模糊集A和B的相應(yīng)規(guī)則的激活強(qiáng)度分別如式(6)所示,且uAi(xi)和uBi(xi)是U=U1×U2×…×Un上的連續(xù)函數(shù),則由式(13)~(16)給出的相似度計(jì)算方法滿足相似性的基本數(shù)學(xué)準(zhǔn)則。
證明 由于該方法對準(zhǔn)則(1)和準(zhǔn)則(2)顯然成立,因此,僅證明準(zhǔn)則(3)~準(zhǔn)則(5)成立。
準(zhǔn)則(3):由于uA(x)≥0,uB(x)≥0,在U上連續(xù),則
?
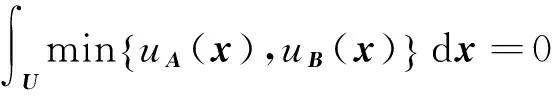


準(zhǔn)則(4):由于uA(x)≥0,uB(x)≥0,在U上連續(xù),則
?

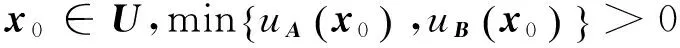

而且, 根據(jù)式(13)~(16),得到
?
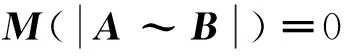


準(zhǔn)則(5):
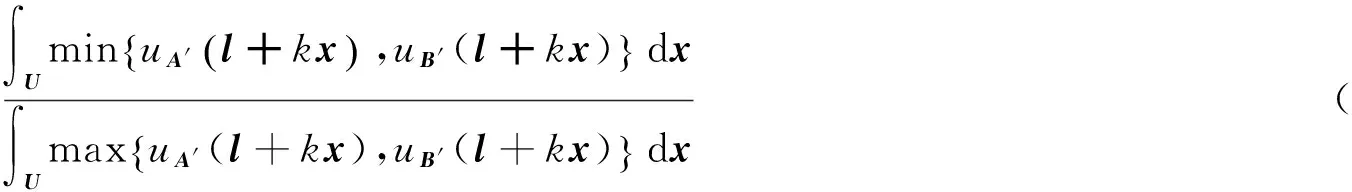
作積分變換y=l+kx,則上式變?yōu)?/p>

證明完畢。
[1]ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353.
[2]TüRKSEN I B, FAZEL ZARANDI M H. Fuzzy system models for aggregate scheduling analysis[J]. International Journal of approximate reasoning, 1998, 19(1/2): 119-143.
[3]FAY A. A fuzzy knowledge-based system for railway traffic control[J]. Engineering applications of artificial intelligence, 2000, 13(6): 719-729.
[4]GE Aaidong, WANG Yuzhen, WEI Airong, et al. Control design for multi-variable fuzzy systems with application to parallel hybrid electric vehicles[J]. Control theory & applications, 2013, 30(8): 998-1004.
[5]CHAO C T, CHEN Y J, TENG C C. Simplification of fuzzy-neural systems using similarity analysis[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 1996, 26(2): 344-354.
[6]CHEN Minyou, LINKENS D A. Rule-base self-generation and simplification for data-driven fuzzy models[J]. Fuzzy sets and systems, 2004, 142(2): 243-265.
[7]TSEKOURAS G E. Fuzzy rule base simplification using multidimensional scaling and constrained optimization[J]. Fuzzy sets and systems, 2016, 297: 46-72.
[8]SETNES M, BABUSKA R, KAYMAK U, et al. Similarity measures in fuzzy rule base simplification[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 1998, 28(3): 376-386.
[9]REZAEE B. Rule base simplification by using a similarity measure of fuzzy sets[J]. Journal of intelligent & fuzzy systems: applications in engineering and technology, 2012, 23(5): 193-201.
[10]PRATAMA M, ANAVATTI S G, LUGHOFER E. GENEFIS: toward an effective localist network[J]. IEEE transactions on fuzzy systems, 2014, 22(3): 547-562.
[11]LIN C T, LEE C S G. Reinforcement structure/parameter learning for neural-network-based fuzzy logic control systems[J]. IEEE transactions on fuzzy systems, 1994, 2(1): 46-63.
[12]LENG Gang, ZENG Xiaojun, KEANE J A. A hybrid learning algorithm with a similarity-based pruning strategy for self-adaptive neuro-fuzzy systems[J]. Applied soft computing, 2009, 9(4): 1354-1366.
[13]HAN Honggui, QIAO Junfei. A self-organizing fuzzy neural network based on a growing-and-pruning algorithm[J]. IEEE transactions on fuzzy systems, 2010, 18(6): 1129-1143.
[14]WANG Xiaojing, ZOU Zhihong, ZOU Hui. Water quality evaluation of Haihe River with fuzzy similarity measure methods[J]. Journal of environmental sciences, 2013, 25(10): 2041-2046.
[15]NGUYEN N N, ZHOU W J, QUEK C. GSETSK: a generic self-evolving TSK fuzzy neural network with a novel Hebbian-based rule reduction approach[J]. Applied soft computing, 2015, 35: 29-42.
[16]ROUBENS M. Pattern classification problems and fuzzy sets[J]. Fuzzy sets and systems, 1978, 1(4): 239-253.
[17]DENG Yong, SHI Wenkang, DU Feng, et al. A new similarity measure of generalized fuzzy numbers and its application to pattern recognition[J]. Pattern recognition letters, 2004, 25(8): 875-883.
[18]CASTELLANO G, FANELLI A M, MENCAR C, et al. Similarity-based Fuzzy clustering for user profiling[C]//Proceedings of 2007 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology Workshops. Silicon Valley, USA, 2007: 75-78.
[19]QIAO Junfei, LI Wei, ZENG Xiaojun, et al. Identification of fuzzy neural networks by forward recursive input-output clustering and accurate similarity analysis[J]. Applied soft computing, 2016, 49: 524-543.
[20]LI Wei, QIAO Junfei, ZENG Xiaojun. Accurate similarity analysis and computing of Gaussian membership functions for FNN simplification[C]//Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery. Zhangjiajie, China, 2015: 402-409.
Computing and performance analysis of similarity between fuzzy rules
LI Wei1,2, QIAO Junfei1,2, HAN Honggui1,2, ZENG Xiaojun3
(1. Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China; 2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China; 3. School of Computer Science, the University of Manchester, Manchester M13 9PL, UK)
Facing the weaknesses of the existing analysis and computing methods for the similarity between fuzzy rules (FRs), this paper investigated the computing methods for the similarity between FRs. First, the similarity between FSs was transferred equivalently into the similarity between multivariable fuzzy sets, and then three application based performance criterions-distinguishability, dimension dependency, and computing complexity were proposed to evaluate the computing methods of the similarity between FRs. Second, four new methods were proposed based on the two existing methods for computing the similarity between FRs, and then the performance analysis and comparison between these new and existing methods were performed. Next, a simulation example for the similarity computing between FRs was provided, and the simulation shows effectiveness of the proposed performance criteria, feasibility of the computing methods, and correctness of the analysis conclusions. The results obtained in this paper provide powerful tools and guides for the similarity analysis and computing of FRs. Inparticular, they establish the methodological foundation and provide a new design approach for the merging of similar FRs in the structure simplification of fuzzy systems and fuzzy neural networks.
fuzzy rules; similarity computing; distinguishability; dimension dependency; computing complexity

李微,女,1985年生,博士研究生,主要研究方向?yàn)橹悄苄畔⑻幚怼?/p>

喬俊飛,男,1968年生,教授,博士生導(dǎo)師,教育部長江學(xué)者特聘教授,國家杰出青年基金獲得者,教育部新世紀(jì)優(yōu)秀人才,中國人工智能學(xué)會科普工作委員會主任,主要研究方向?yàn)橹悄苄畔⑻幚怼⒅悄芸刂评碚撆c應(yīng)用。獲教育部科技進(jìn)步獎一等獎和北京市科學(xué)技術(shù)獎三等獎各1項(xiàng)。發(fā)表學(xué)術(shù)論文100余篇,被SCI檢索20余篇,EI檢索60余篇。
韓紅桂,男,1983年生,教授,博士生導(dǎo)師,入選國家自然科學(xué)基金優(yōu)秀青年科學(xué)基金、中國科協(xié)青年人才托舉工程等,主要研究方向?yàn)橹悄芴卣鹘!⒆越M織模糊控制和多目標(biāo)智能優(yōu)化。發(fā)表學(xué)術(shù)論文60余篇。
10.11992/tis.201512040
http://kns.cnki.net/kcms/detail/23.1538.TP.20170227.1758.004.html
2015-12-22.
日期:2017-02-27.
國家自然科學(xué)基金項(xiàng)目(6162200417, 61533002, 61225016);中國博士后科學(xué)基金項(xiàng)目(2014M550017);北京市教育委員會科研計(jì)劃項(xiàng)目(KZ201410005002,km201410005001);高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金項(xiàng)目(20131103110016).
喬俊飛. E-mail:isibox@sina.com.
TP18
A
1673-4785(2017)01-0124-08
李微,喬俊飛,韓紅桂,等.模糊規(guī)則相似性計(jì)算與性能分析研究[J]. 智能系統(tǒng)學(xué)報(bào), 2017, 12(1): 124-131.
英文引用格式:LI Wei, QIAO Junfei, HAN Honggui, et al.Computing and performance analysis of similarity between fuzzy rules[J]. CAAI transactions on intelligent systems, 2017, 12(1): 124-131.

