有關費爾馬小定理的推廣
楊燕妮
(喀什大學 數學與統計學院,新疆 喀什 844006)
有關費爾馬小定理的推廣
楊燕妮
(喀什大學 數學與統計學院,新疆 喀什 844006)
首先用數學歸納法證明了費爾馬小定理,然后通過模p數系乘法的代數結構,不僅導出了公式,同時也證明了費爾馬小定理。進一步將此方法推廣到了一般模n和任何有限交換群上。最后,借助拉格朗日定理建立了有限非交換群上同樣的公式。可見,費爾馬小定理是群論最基本的拉格朗日定理之特例。
交換群;非交換群;費爾馬小定理;歐拉定理;拉格朗日定理
費爾馬小定理[1]是近代密碼學瑞沙葉算法[2-3]的理論基礎。本文從費爾馬小定理的證明出發,分析與p互素的整數在乘法運算下的代數結構,并將其推廣到非素數n對應的歐拉定理[4]和一般抽象群的元素上。最終發現費爾馬小定理竟然是群論中拉格朗日定理[5]的簡單推論。
1 費爾馬小定理的歸納法證明
費爾馬小定理 設p為一正素數,若a∈且p|a,則:ap-1≡1(modp),?a∈,p|a。
(1)
眾所周知,數學歸納法僅適用于正整數。因此,需先對a作歸納,然后再推廣到任意整數。此外,數學歸納法的關鍵是由a的p-1次方推出a+1的p-1次方。但在模p下,要將(a+1)p-1展開化簡并不易。若將a+1取p次方,然后再模p則簡單的多。事實上,由二項式定理可知,(a+1)p的展開式中,除頭尾兩項的系數是1外,其余都是p的倍數,即:
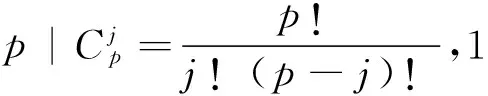
上式分母中的所有整數因子均小于p,因此分子中的p不會被約掉。從而:(a+1)p≡ap+1(modp)。
顯然,這里的項數2可被任何正整數取代。換句話說,“和的p次方等于p次方的和”。可見:在模p的環境下,只需將結論中的次方轉化成p次方即可。為此,將等式兩邊同乘以a,有ap≡a(modp)。當p|a時,此同余式與原同余式等價。
數學歸納法必須針對所有正整數,不能排除p的倍數。然而,條件卻限制了p|a,怎么辦?注意到,修改版ap≡a(modp)對p的倍數顯然成立。因此,只需用數學歸納法證明:
ap≡a(modp),?a∈即可。
(2)
證明:(1)當a=1時,因1p≡1(modp),故同余式(2)成立;
(2)假設當a=k時,同余式(2)成立,即kp≡k(modp)。于是,(k+1)p≡kp+1≡k+1(modp)。即當a=k+1時,(2)也成立.由歸納原理可知,ap≡a(modp),?a∈成立。
進一步,當a=0時,同余式(2)顯然成立。對負整數a=-k,k∈和正素數p≠2,由于:
(-k)p=-kp?ap=(-k)p=-(kp)≡-k=a(modp),
此時(2)成立。當p=2時,因1+1≡0(mod2)。故-1≡1(mod2)。因此,(-k)p≡-kp(modp)恒成立。
綜上可知,同余式ap≡a(modp),對?a∈成立,于是費爾馬小定理得證。
2 完全剩余系與費爾馬小定理
眾所周知,雖然整數有無窮多,但是其模p后只剩p個余數0,1,2,…,p-1。通常用p表示在模p的加法和乘法下形成的代數結構(p,+,·)。費爾馬小定理就是在此有限體的乘法結構中產生的,其中且是一個交換群[4]。下面,在這個有限交換群上來構建費爾馬小定理。
設a∈,且p|a,即(p,a)=1。群包含p-1個元素,它恰是定理中a的次冪。顯然,用a乘以群中的每個數,可得包含p-1個a的倍數的集合:
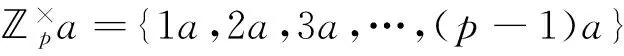
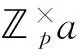
(1a)(2a)…(p-1)a≡1·2…(p-1)(modp)或(p-1)!ap-1≡(p-1)!(modp)。
由消去律即得費爾馬小定理ap-1≡1(modp)。
3 費爾馬小定理與歐拉定理
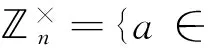
其元素個數等于歐拉函數φ(n),即小于n且與n互素的正整數個數。它同樣具有交換群的代數結構[5]。現用與上節同樣的方法來構建將費爾馬小定理推廣到一般模n的公式。
設a∈,且(a,n)=1。令考慮用a乘以群中每個數所得的集合
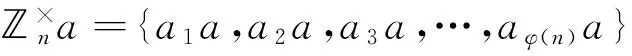
由消去律可知,其中的元素兩兩互異。于是
再由交換律可得:
(a1a2…aφ(n))aφ(n)≡a1a2…aφ(n)(modn)。
兩邊消去a1a2…aφ(n)后,就得到了費爾馬小定理的推廣——歐拉定理。
歐拉定理若a∈且(a,n)=1,則aφ(n)≡1(modn)。
4 有限交換群上的費爾馬小定理
總結前兩節的論證過程,一般可歸納為三個步驟:首先,在模環境下,利用消去律把看似不同的兩個集合Ga與G同歸于一;其次,將集合Ga中所有元素相乘,并利用交換律把a表成方冪形式;最后,再利用消去律即得所求公式。可見,論證的本質在于G是有限交換群。為此,可將公式(1)推廣到一般有限交換群上。
定理 設G是含有m個元素的交換群。若a∈G,則am=e,其中e為G的單位元。
證明:令G={a1,a2,…,am}。由消去律可知,Ga={a1a,a2a,…,ama}中的元素兩兩互異.于是,Ga=G.將Ga與G中的所有元素分別各自相乘,再由交換律將a表成方冪形式,可得:
(a1a2…?am)am=(a1a2…?am)。
消去a1a2…?am就得到am=e。
5 有限非交換群上的費爾馬小定理
在含有m個元素的非交換群G里,am=e,?a∈G是否成立?顯然,沒有交換性,要把元素a表為方冪形式很難。為此,考慮群G中由元素a生成的循環子群={an|n∈} 反過來,T(a)|m是否也是am=e的充分條件呢?為此,令A=且k=T(a)。若A=G,則m=T(a),結論成立;若A≠G,則?b∈G但b?A。現將已有的元素列表如下: a,a2,a3,…,ak-1,e ab,a2b,a3b,…,ak-1b,b. 由消去律不難看出,第二行的所有元素不僅兩兩相異,而且也不同于第一行的所有元素(若aib=aj,則b=aj-i∈A,與假設b?A矛盾)。上表中共有2·T(a)個元素。若它們就是G的所有元素,則結論已成立。否則,再選取不在這兩行的元素c,并考慮下面新的列表: a,a2,a3,…,ak-1,e ab,a2b,a3b,…,ak-1b,b ac,a2c,a3c,…,ak-1c,c. 由消去律同樣可知,第三行的所有元素兩兩相異且不同于前兩行的所有元素。上表中共有3·T(a)個元素。如此繼續下去,每次構造出的新元素均為T(a)個。因G是有限群,故在有限步后,不妨設為s,就會遍歷G中的所有元素。因此,可得m=s·T(a),即T(a)|m。 設H 拉格朗日定理 設G是有限群。若H 證明:仿上節的論證,只需將方冪移至下標H={a1,…,ak-1,ak=e}即可(略)。 推論1 設G是有限群且T(G)=p。若p為素數,則G是循環群。 證明:取非單位元a∈G且令H=,則1 推論2 若G是有限群且a∈G,則T(a)|T(G)。 證明:令H=,則T(a)=T(H)|T(G),得證。 推論3 若G是有限群且a∈G,則aT(G)=e。 證明:由推論2知T(a)|T(G)。設T(G)=r·T(a),r∈.于是,aT(G)=ar·T(a)=(aT(a))r=er=e。 推論4 設n∈,a∈。若(a,n)=1,則aφ(n)≡1(modn)。 推論5 設p是正素數,a∈。若p|a,則ap-1≡1mod(p)。 事實表明,費爾馬小定理的確是拉格朗日定理的特例。 [1] 鄧勇.費爾馬小定理的一種奇特證明[J].首都師范大學學報(自然科學版),2015,36(2):8-9. [2] 陳少真.密碼學基礎[M].北京:科學出版社,2008. [3] 肖攸安,李臘元.數字簽名技術的研究[J].武漢理工大學學報(交通科學與工程版),2002,26(6):737-740. [4] 張文鵬,李海龍.初等數論[M].西安:陜西師范大學出版社,2013. [5] 張禾瑞.近世代數基礎(修訂本)[M].北京:高等教育出版社,2010. 責任編輯:程艷艷 OnGeneralizationofFermat’sLittleTheorem YANGYanni (CollegeofMathematicsandStatistics,KashgarUniversity,Kashgar844006,China) Firstly, Fermat’s little theorem was proved by using mathematical induction. Secondly, the formula was obtained and Fermat’s little theorem was proved by using algebraic structure of residues system multiplication of modulop. Thirdly, this method was extended to the general residues system of modulonand any finite abelian group. Finally, the same formula was established on finite non-abelian group by using Lagrange’s theorem. The fact shows that Fermat’s little theorem is a special case of the most basic Lagrange’s theorem in group theory. abelian group; non-abelian group; Fermat’s Little Theorem; Euler’s Theorem; Lagrange’s Theorem 2017-03-27 新疆維吾爾自治區自然科學基金項目(2016D01A014) 楊燕妮(1988-),女,甘肅靜寧人,助教,碩士,主要從事代數方面研究。 O156 A 1009-3907(2017)04-0029-046 拉格朗日定理

