基于幾何特征的整體葉輪三維測量模型與CAD模型對齊方法

邢曉紅 郭明森 黃金昌

1.南京航空航天大學金城學院機電工程系，南京，211156 2.南京航空航天大學精密驅動研究所，南京，210016 3.沈陽飛機設計研究所,沈陽，110035

基于幾何特征的整體葉輪三維測量模型與CAD模型對齊方法

邢曉紅1郭明森2黃金昌3

1.南京航空航天大學金城學院機電工程系，南京，211156 2.南京航空航天大學精密驅動研究所，南京，210016 3.沈陽飛機設計研究所,沈陽，110035

提出了基于幾何特征的模型對齊方法，并應用于整體葉輪三維模型。提取了測量模型的質心。根據整體葉輪對稱性，采用最小二乘法對其軸線進行了估算，并采用加工精度高的軸位置數據對軸線進行了修正，從而將測量模型的質心、軸線與CAD模型的質心及軸線對齊。根據整體葉輪的制造精度特征，采用加權最小二乘法，實現了葉片區域測量模型與CAD模型的對齊。經計算，采用上述方法的最大對齊誤差為0.2 mm。

整體葉輪；幾何特征；三維測量；對齊

0 引言

整體葉輪是透平機械的核心，也是各類航空發動機的關鍵部件，已經廣泛地用于航空、航天及其他工業領域。目前整體葉輪加工一般采用鑄造加工、電火花加工、電解加工及數控銑削加工等方法。數控加工柔性好，可加工復雜形狀葉輪，且表面質量好、效率高、適用廣泛，因此五坐標數控銑削加工也是整體葉輪加工常采用的方法之一[1-2]。

數控加工后的檢測是必不可少的步驟，檢測結果可以幫助工藝人員和數控編程人員發現存在的問題，并針對問題提出適當的解決辦法。就整體葉輪的測量方法而言，目前主要有三種方法，即型面樣板檢測法、三坐標測量機檢測法以及光學檢測法。整體葉輪葉片型面測量的趨勢是使用光學檢測法。在測量效率上，采用光學檢測法的測量速度要比型面樣板以及三坐標方法高數個數量級，并且能夠覆蓋被測零件的大部分表面甚至全部表面，且該方法對環境要求小，適用于現場測量。

對于光學檢測法，在對測量數據進行分析前，需要將測量坐標系與建模坐標系對齊。在測量過程中其測量坐標系是根據測量儀器自身系統建立的，這個坐標系與建模坐標系一般不會一致，因此需要在測得數據后進行對齊操作。文獻[3-4]研究了單個葉片的對齊及測量分析方法。然而對于整體葉輪三維測量模型與CAD模型的對齊方法研究還未有文獻報道。

在對光學測量儀測得的整體葉輪點云數據模型進行坐標對齊操作的過程中，由于葉輪上帶有孔的內表面很難測得，且整體葉輪類零件屬于軸對稱，因此難以確定其測量坐標系。本文提出了一套整體葉輪測量坐標系與建模坐標系對齊方法。

1 整體葉輪對齊方法

圖1所示為采用ATOS光學測量儀器測得的STL數據模型。整體葉輪零件對齊過程即通過調整其6個自由度(3個平移自由度和3個旋轉自由度)，通過某種算法將測量模型與原始CAD模型進行對齊。這個過程與經典的最近點迭代(iterative closest point，ICP)方法的思想是一致的[5]。傳統的最近點迭代方法對測量數據進行配準定位計算時，根據測量數據在CAD模型表面求取最近點集，再進行變換迭代。

圖1 整體葉輪測量數據模型Fig.1 Measured data model of integral impeller

整體葉輪不同于自由曲面零件，該類零件具有明顯的設計特征，即整體葉輪是一個典型的繞軸旋轉工作零件，因此，對其軸線的估計是模型對齊的基礎。根據測量數據點到對稱軸線距離的平方和為最小來對軸線進行估算。將質心位置移動到建模坐標系下模型質心位置，并使其軸線對齊。此時，測量數據限制了沿X、Y、Z軸的平動以及繞X、Y軸的轉動。余下一個自由度，即繞Z軸的轉動自由度需要確定。在這個自由度(繞Z軸的旋轉)的對齊問題上，本文直接采用測量模型與CAD模型進行對齊，并且針對葉片存在的變形問題，提出一種加權最小二乘對齊方法。

2 具體算法及流程

2.1 質心

設STL模型中的數據點為pi=(xi,yi,zi)，i=1,2,…，n，則該模型的質心可估算為[6]

(1)

絕對均勻的整體葉輪零件的質心應位于其軸線上。質心估計的意義在于可以為其軸線的計算提供基礎。

2.2 旋轉軸線

本文利用各點到軸線距離平方和最小這個特點，采用最小二乘方法對模型軸線進行估計。

圖2所示為空間點和一條空間直線。po為直線上一點，也就是式(1)中的質心。設該直線方向矢量為v，并設其為單位矢量，即|v|=1；pi為直線外一點，計算點pi到直線的距離di的標準公式為

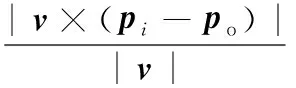
(2)

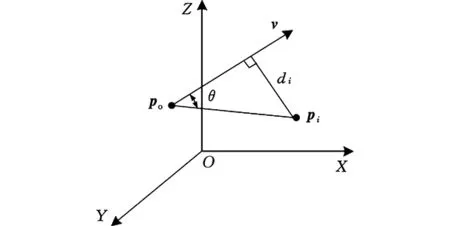
圖2 空間點到直線的距離Fig.2 The distance between a point and a line

由于|v|=1，則式(2)可簡化為

di=|v×(pi-po)|

(3)

根據向量的向量積性質，式(3)可以繼續簡化為

di=|v||pi-po|sinθ=|pi-po|sinθ

(4)

設v=(α,β,γ)，其中α2+β2+γ2=1，po=(xo,yo,zo)，取測量數據點到軸線距離的平方和為目標函數，并計算其極小值，即有

(5)

分別對α，β，γ求偏導，并令其為0，則可得以下方程組：

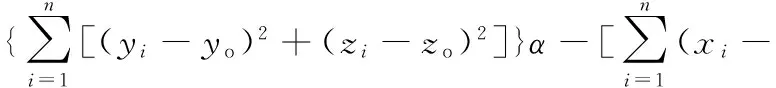
方程組系數矩陣為一對稱矩陣。在求解過程中不需要計算出具體的數值，只需要得到α/β以及β/γ即可。

通過以上方法可估算出軸對稱零件的軸線。若測量數據足夠均勻，則該方法可以得到近似程度較高的結果。圖3中的理想模型來自UG軟件。

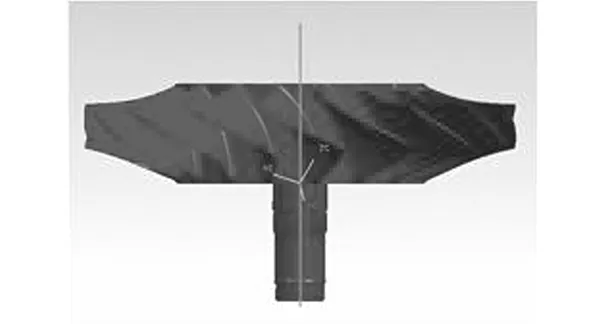
圖3 理想模型旋轉軸最小二乘估計Fig.3 Therotational axis estimated by least square algorithm from ideal model

2.3 旋轉軸位置修正

由于在測量過程中存在測量儀器的誤差以及測量盲區等問題，往往所采集的點云數據并不十分均勻，因此通過2.2節方法所得到的結果并不一定能令人滿意，只能實現大致的對齊，如圖4所示。

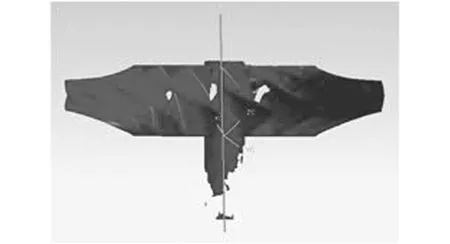
圖4 測量模型旋轉軸最小二乘估計Fig.4 The rotational axis estimated by least square algorithm from measured model

由圖3、圖4可以明顯看出，計算得到的軸線與所測數據模型的實際軸線存在一定偏差，這需要對該軸線進行修正。本文針對整體葉輪的制造特征提出了精確軸線提取方法。

整體葉輪類零件是一類旋轉工作零件，因此在制造過程中對整體葉輪的旋轉軸有著極高的精度要求，軸在裝配過程中起著重要的定位作用。因此，可提取測量模型軸位置數據作為葉輪旋轉軸線精確估計的依據。

為簡化該問題，將上一節中得到的軸線通過旋轉操作使其與Z軸重合。垂直于該軸線(即Z軸)建立截平面，得到該平面與軸位置測量數據模型的交點。通常情況下，該截面是一個橢圓。

本文通過截取數個軸位置截面數據，計算每個截面數據的中心，并將所有中心點數據擬合成一條直線，即為軸線的精確估計。同時，該軸線應通過CAD模型的質心以及CAD模型所在坐標系的原點。考慮到對橢圓擬合比較復雜，而根據橢圓的對稱性可知，采用圓對其進行擬合即可。擬合方法如下[7]：

只考慮數據點在OXY平面上的投影，設該組數據點為(xj,yj)。設假想的圓心坐標為(xc,yc)，圓的半徑為R，則與該組數據點的距離平方和為最小的圓的方程為

(x-xc)2+(y-yc)2=R2

建立目標函數如下：

為避免求導的復雜，上式中沒有采用距離的平方和最小為目標函數。計算該函數的極小值，便可得到三個未知量，如圖5所示。

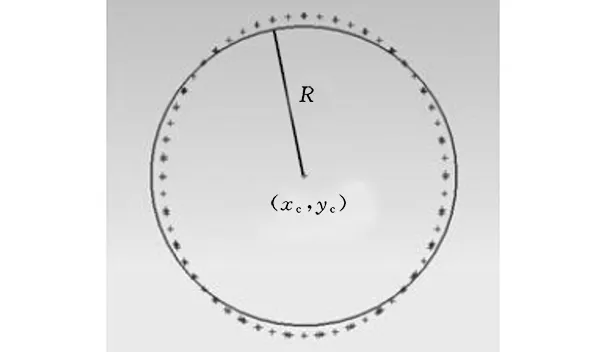
圖5 橢圓的圓弧擬合Fig.5 Arc fitting of an ellipse

沿Z軸方向截取葉輪測量模型軸上m個截面數據，并采用上述方法對每個截面數據進行擬合，得到m個圓心位置，采用直線對這m個圓心位置進行擬合，擬合后的直線可作為修正后的整體葉輪測量數據模型的旋轉軸線，如圖6所示。

2.4 葉片曲面的對齊

通常在對整體葉輪的葉片型面檢測過程中，并不需要對整個葉片型面的數據點進行檢驗，而只檢驗設定好的幾個截面，因此可根據測量葉片型面與CAD葉片型面相對應截面數據之間的關系來進行對齊工作。由此可知，仍可采用經典的最小二乘法進行對齊。

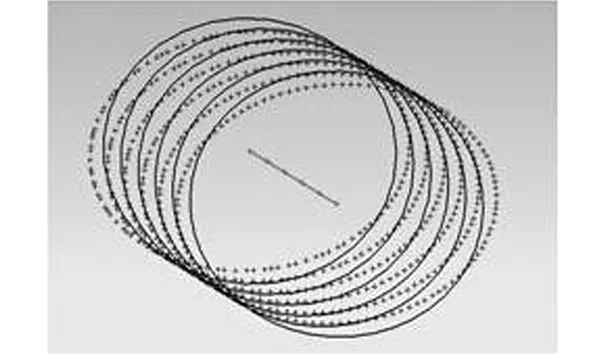
(a)橢圓中心直線擬合

(b)修正后的測量模型軸線圖6 測量模型軸線修正Fig.6 Modification of measured model axis

由經驗可知，葉片在加工過程中一般存在變形，且變形量從葉尖到葉根逐漸減小。傳統的最小二乘法是使測量數據點與葉片型面距離的平方和最小，卻不一定符合實際情況。在對齊過程中，各個截面所需考慮的精度不同，即每個截面數據在對齊過程中所占的權重不同。

基于以上分析，本文采用加權最小二乘法對葉片型面進行匹配。

2.4.1 截面數據的選取

葉片的設計數據是由垂直于某個坐標軸的數個截面數據點定義的。當葉輪測量模型與CAD模型完全重合時，其中有一個葉片的測量模型與最原始的設計葉片重合，此時可以基于原始的截面定義位置，截取該葉片測量模型相應位置上的數據作為對齊數據依據。然而由分析可知，在葉片對齊之前，葉片部分的數據模型與CAD模型一般是不重合的，以這種方法得不到所需數據。由此，本文采用的方法是繞葉輪旋轉軸線并以各個設計截面位置高度為半徑作一系列的圓柱面，取得該圓柱面與測量模型的交點，以這些點作為依據，進行對齊工作。圖7所示為一組葉片截面數據。

圖7 一組葉片截面數據示意圖Fig.7 Schematic of cross section data of blade

2.4.2 權值的確定以及目標函數的建立

在整體葉輪設計過程中，對葉片型面有公差要求，即需給出最大葉型偏差允許值。葉片出現最大葉型偏差的位置應位于其葉尖處，而葉片與輪轂的交線處的偏差最小，可認為沒有偏差。

設存在p組截面，各組截面數據的權值計算如下：

計算各組截面與輪轂曲面之間的距離sk(1≤k≤p)，其中最大距離為smax；計算每個截面到輪轂的距離與最大距離的比值為sk/smax；則本文取每個截面的權值λk=smax/sk，表示在匹配過程中，越靠近輪轂截面的數據越受重視，越應該靠近設計葉片型面。

得到權值后，建立基于加權最小二乘的目標函數：

其中，q代表每組截面具有q個數據點；dkl表示第k組截面上的第l個數據點與CAD模型葉片相應截面上最近點之間的距離，可通過UG/Open API提供的函數得到。

對該目標函數進行求解，其中距離可看作旋轉角度的函數，求解出目標函數最小值對應的旋轉角度。將測量模型數據根據該角度旋轉，便可實現與CAD模型的對齊。

2.5 對齊結果

CAD模型與測量模型對齊結果如圖8所示。采用ATOS軟件自帶手動對齊方法，得到測量模型與設計模型的最大對齊誤差為0.5mm，而采用本文方法所得到的最大對齊誤差為0.2mm。

圖8 CAD模型與測量模型對齊結果Fig.8 Result of aligning measured model with CAD model

3 結論

本文提出了基于幾何特征的三維測量模型與CAD模型對齊方法，并將此方法應用于整體葉輪的三維模型中。經計算，采用本文方法得到的最大對齊誤差為0.2mm。

[1] 陳晧暉，劉華明，李剛，等. 復雜曲面葉輪CAD/CAM一體化系統開發[J]. 航天制造技術，2003(2):28-31.CHENHaohui,LIUHuaming,LIGang,etal.DevelopmentofCAD/CAMIntegralSystemforComplexCurvedImpeller[J].AerospaceManufacturingTechnology, 2003(2):28-31.

[2] 吳寶海，王尚錦. 自由曲面葉輪的四坐標數控加工研究[J]. 航空學報，2007，28(4):993-998.WUBaohai,WANGShangjin.Researchon4-axisNumericalControlMachiningofFree-formSurfaceImpellers[J].ActaAeronauticaetAstronauticaSinica, 2007, 28(4):993-998.

[3] 呂彥明，滕樹新. 汽輪機葉片截型測量數據的自動分析[J]. 工具技術，2007，41(7):94-95.LYUYanming,TENGShuxin.AutomaticAnalysisofMeasuringDataofSectionalProfileonTurbineBlade[J].ToolEngineering, 2007,41(7):94-95.

[4] 陳福興. 基于UG葉片型面測量分析技術的研究[D]. 無錫:江南大學，2006.CHENFuxing.ResearchonMeasurementandAnalysisTechnologyofBlade’sSurface[D].Wuxi:JiangnanUniversity, 2006.

[5]BESLPJ,MCKAYND.AMethodforRegistrationof3-DShapes[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1992,14(2):239-256.

[6] 王堅. 非規則碎片拼合關鍵技術研究[D]. 南京:南京航空航天大學，2007.WANGJian.ResearchonKeyTechnologyofIrregularFragmentsReassembly[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics, 2007.

[7] 雷家勇，達飛鵬，孟廣猛. 圖像處理中圓心算法研究[J]. 計算機與現代化，2005(3):25-26.LEIJiayong,DAFeipeng,MENGGuangmeng.ArithmeticofComputingCenterofCircleinComputerImageProcessing[J].ComputerandModernization, 2005(3):25-26.

(編輯 王旻玥)

An Aligning Method for 3D Measured Model with CAD Model of Integral Impeller Based on Geometric Features

XING Xiaohong1GUO Mingsen2HUANG Jinchang3

1.Mechanical and Electronic Engineering Department,NanHang Jincheng College,Nanjing,211156 2.Laboratory of Precision Drive,Nanjing University of Aeronautics and Astronautics,Nanjing,210016 3.Shenyang Aircraft Design and Research Institute,Shenyang,110035

A model alignment method was proposed based on geometric features, and applied to a 3D model of integral impellers. First, centroid of the measured models was extracted. According to the symmetry features of the integral impeller, the least square algorithm was utilized to estimate the rotational axis and was modified by the more accurate data of shaft part. Therefore, the centroids and rotational axes of the measured models were aligned with those of the CAD models. Then, the aligning of the blade parts of the measured models with the CAD models was realized by using weighted least squares method according to the characteristics of manufacture precision. The maximum alignment deviation caused by the proposed method is as 0.2 mm.

integral impeller； geometric feature； 3D measurement； alignment

2016-07-11

江蘇省大學生創新創業訓練計劃項目(201613655016X)

TG806

10.3969/j.issn.1004-132X.2017.10.012

邢曉紅，女，1980年生。南京航空航天大學金城學院機電工程系講師。主要研究方向為數控加工技術和模具設計及制造。E-mail:xingxh@nuaa.edu.cn。郭明森，男，1980年生。南京航空航天大學航空宇航學院副教授、博士。黃金昌，男，1980年生。沈陽飛機設計研究所高級工程師。