基于高溫蠕變特性的連鑄坯新矯直技術

張興中 郭 龍 馮常喜

燕山大學國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

基于高溫蠕變特性的連鑄坯新矯直技術

張興中 郭 龍 馮常喜

燕山大學國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

基于目前工廠常用的連鑄坯矯直技術，考慮連鑄坯在高溫下的蠕變特性，提出利用高溫蠕變對連鑄坯進行蠕變矯直的新觀點。針對某鋼廠R9300連鑄機設計了一條新型的曲率變化滿足正弦規律且彎曲段和矯直段弧長顯著延長的矯直曲線，通過數值模擬計算和對比分析，新矯直曲線的應變速率更低，矯直過程中可以充分利用材料的高溫蠕變性能。通過在Gleeble-3800型熱/力模擬試驗機上對Q460E鋼進行熱塑性試驗和蠕變拉伸試驗，確定了該鋼種的相關熱物性參數和蠕變本構方程。由于新曲線矯直區的應變速率接近最小蠕變應變速率，連鑄坯主要依靠高溫蠕變變形進行矯直，降低了應變速率，可以避免連鑄坯內部裂紋缺陷，有利于提高連鑄坯的質量。

連鑄坯；蠕變矯直；應變速率；矯直曲線

0 引言

連續鑄鋼是鋼鐵生產流程中的重要組成部分。進入21世紀以后，世界鋼鐵行業連鑄比超過90%[1]，2004年以后我國鋼鐵行業的連鑄比超過96%[2]。連鑄坯的內部裂紋是連鑄生產過程中的主要缺陷，它不僅影響到連鑄坯的質量還影響到后續的軋制過程[3]。連鑄坯在彎曲矯直過程中處于800～1400 ℃的高溫，而且受力復雜，很容易在內部和固液交界面產生裂紋[4]。由于金屬在溫度高于自身熔點溫度的0.3倍時蠕變現象十分明顯，因此連鑄坯在彎曲矯直過程中具有明顯的蠕變行為。

早期研究中，GRILL等[5]采用彈性和蠕變模型來預測連鑄坯的鼓肚變形。OKAMURA等[6]采用彈-塑性和蠕變有限元方法研究了蠕變對連鑄坯鼓肚變形的影響。 近年來， HUESPE等[7]采用彈-黏-塑性模型研究了圓形連鑄坯的蠕變性能，并分析了其在整個連鑄過程的應力狀態。滿媛等[8-9]對連鑄坯在連續矯直過程中的高溫蠕變行為做了大量的工作，并且提出了具有兩個連續矯直區的新機型曲線。馬春武等[10]對廣泛使用的三次連續矯直曲線進行了應力應變分析，認為連鑄坯在一定外力作用下會發生明顯的蠕變行為。景奉儒等[11]對直弧型板坯連鑄機連續彎曲矯直曲線進行了優化，提出彎曲與矯直應采用不同的應變速率來適應金屬溫度高、蠕變快的規律。這些學者都認為連鑄坯在彎曲矯直變形過程中，要充分考慮蠕變的影響。黃文等[12]對多點矯直直弧型連鑄機的矯直反力進行了計算。李寧[13]對薄板坯連鑄機連續矯直區的矯直力和力矩的計算方法進行了研究。

這些研究都表明連鑄坯在矯直變形時矯直力必須大于屈服強度，并沒有充分考慮金屬的高溫蠕變特性。由于金屬在高溫低于屈服強度的應力作用下也會發生較快的永久變形，因此本文提出利用材料的這一高溫蠕變特性，使連鑄坯在彎曲矯直變形過程中主要依靠蠕變變形，降低連鑄坯的矯直應力，避免內部裂紋的發生，從而提高連鑄坯的質量。

1 理論基礎

根據平截面假設，鑄坯中性層在彎曲矯直過程中不發生伸長或縮短，因此連鑄坯表面下某一層的彎曲矯直應變可以表示為

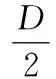
(1)

式中，εh為連鑄坯某一層的應變；D為連鑄坯厚度，mm；h為連鑄坯某一層到中距離厚度，mm；ki為連鑄坯在彎曲矯直開始點曲率，mm-1；ki+1為彎曲矯直結束點曲率，mm-1；i為彎曲矯直點序號。

由式(1)可以看出，連鑄機機型曲線的曲率直接影響連鑄坯的變形，由于圓弧曲率恒定，因此連鑄坯在基本圓弧段時并不發生變形。目前工廠常用的各種連鑄機機型都存在很長的基本圓弧段，因此縮短基本圓弧段長度，延長彎曲矯直段長度，可以增加連鑄坯蠕變時間，發生更多的蠕變變形。由于多點矯直技術的多段圓弧連接點存在曲率突變，使連鑄坯在每個矯直點產生應變突變，而連續矯直技術的曲率變化是連續的，因此將式(1)對時間進行求導，得到應變速率與曲率相對于弧長變化率的關系：

(2)

由式(2)可知，連鑄機機型曲線的曲率變化率越小，連鑄坯在彎曲矯直變形過程的應變速率越小，因此，選取一條合適的連鑄機機型曲線，使其具有較小的曲率變化率和較長的彎曲和矯直弧長，可以增加連鑄坯在彎曲矯直過程中蠕變的時間，發生更多的蠕變變形，并且使連鑄坯在彎曲矯直段的應變速率更小。當應變速率小于屈服應力作用下的蠕變應變速率時，此時連鑄坯的彎曲矯直變形過程中只存在蠕變變形，沒有塑性變形。

2 機型曲線設計

本文以具有代表性的板坯直弧型連鑄機為例，討論蠕變矯直曲線的設計方法。連鑄坯在彎曲過程中，曲線的曲率必須由0單調增至1/R，然后是一段半徑為R的基本圓弧段，在矯直過程中，曲線的曲率必須由1/R單調減小至0。根據這些邊界條件構造一條曲率滿足正弦規律，曲率變化率滿足余弦規律的機型曲線，其曲率和曲率變化率的表達式如下：

(3)

(4)

0≤s≤L

式中，R為連鑄機基本圓弧半徑，mm；L為彎曲段或矯直段總弧長，mm。

根據弧微分公式，曲線轉角與弧長的關系可以表示為

(5)

式中，α為曲線轉角，rad。

直角坐標系下的橫縱坐標與轉角可以表示為

(6)

因此，該曲線在直角坐標系下的參數方程如下：

(7)

由式(7)可知，當基本圓弧半徑和彎曲、矯直段總弧長確定時，該曲線唯一確定。該曲線的彎曲段與矯直段分別選擇不同的曲線起始點，在彎曲起始點處s1為0時,曲率k1為0，與垂直段相切；在彎曲結束點處s1為L時，曲率k1為1/R，與基本圓弧段相切。同理在矯直段，起始點處s2為0時,曲率k1為0，與水平段相切；在矯直結束點處s2為L時，曲率k2為1/R，與基本圓弧段相切。通過平移和旋轉坐標系，整條曲線可以光滑連接。

3 曲線實例計算

3.1 曲線參數計算

以某鋼鐵廠R9300五點彎曲五點矯直直弧型板坯連鑄機為例，該機型曲線的參數見表1。

表1 R9300機型曲線參數

連鑄機最小圓弧半徑的取值與連鑄坯斷面形狀和澆注的鋼種有關。基本圓弧半徑的計算公式如下：

(8)

式中,D為最大鑄坯的厚度，mm；ε為連鑄坯內弧表面允許應變值，一般ε取1.5%～2.0%。

針對某鋼廠R9300連鑄機的工藝參數，鑄坯厚度為230 mm，許用應變值取為1.5%[14]，將上述基本參數代入式(8)可得連鑄機基本圓弧半徑值：

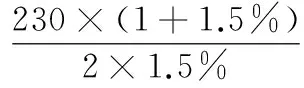
取最小整數圓弧半徑為8000 mm。由于連鑄坯所處溫度越高，蠕變速率越快，為更好地利用蠕變規律，需要連鑄機連續彎曲矯直曲線在溫度高的位置曲率變化率大，溫度低的位置曲率變化率小。綜合考慮原機型的高度和拉坯速度的影響，分別以彎曲段弧長8000 mm和矯直段弧長10 000 mm進行曲線計算。彎曲和矯直曲線計算時初始坐標系不同，如圖1所示。

圖1 彎曲矯直曲線初始坐標系Fig.1 Original coordinate system of curves

通過坐標系平移和旋轉，在同一坐標系下，彎曲段在連接點處的切線斜率為1.3526，而矯直段在連接點處的切線斜率為1.0210，可以看出彎曲段曲線與矯直段曲線在連接點M處無法光滑連接，引入一小段圓弧作為基本圓弧段，考慮鑄機高度會影響連鑄坯的鼓肚變形，因此最終該圓弧的起始圓心角為-0.7393 rad，終止圓心角為-0.9794 rad，通過該段基本圓弧可將矯直曲線和彎曲曲線光滑無突變地連接起來。

基于原R9300五點彎曲五點矯直直弧型連鑄機設計的曲率正弦變化機型曲線參數如表2所示。機型曲線輥列圖如圖2所示。新曲線彎曲段CD弧長8000 mm，基本圓弧段BC弧長1920.8 mm，矯直段AB弧長10 000 mm。

表2 曲率正弦曲線基本參數

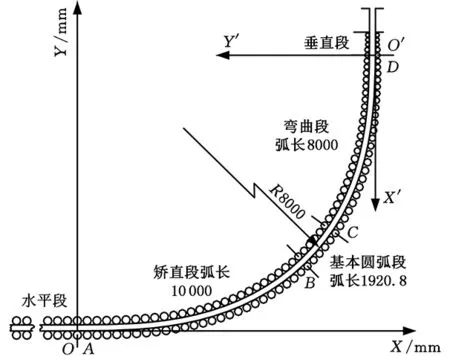
圖2 曲率正弦變化機型曲線輥列圖Fig.2 Roller curve of new casting machine

圖3清晰地表示出五點彎曲五點矯直的機型曲線與曲率滿足正弦規律的機型曲線的曲率變化情況。由圖3可以看出，多點矯直技術在矯直點處曲率存在突變，而新曲率正弦變化機型曲線的曲率變化連續，并且新曲線基本圓弧段顯著縮短，矯直段和彎曲段弧長大大延長，有利于增加蠕變變形和減小應變速率。根據式(2)，新曲線矯直段內弧側表面的應變速率可以由下式計算：

(9)

圖3 兩種機型曲線曲率對比圖Fig.3 Curvature of two casting machines

內弧表面應變速率的理論最大值為5.65×10-5s-1，位于矯直開始點，而在整個矯直過程中，應變速率滿足余弦規律，由最大值單調遞減為0。

3.2 數值模擬計算

根據某鋼鐵廠R9300連鑄機鑄坯斷面尺寸1000 mm×230 mm和兩種不同的機型輥列建立有限元模型。圖4所示為曲率正弦變化機型輥列的有限元計算模型。

圖4 曲率正弦變化機型曲線有限元計算模型Fig.4 Finite element model of new casting machine

為了精確對比兩種矯直技術的效果，兩種曲線模型均采用相同設定，鑄坯尺寸相同，采用相同輥徑和間隙并均勻布置，忽略了溫度場、重力、鋼水靜壓力等參數對其應變造成的影響，通過各個連鑄輥轉動摩擦力帶動鑄坯沿曲線位置以工廠實際拉速1.5 m/min勻速運動[15]。由于連鑄坯在矯直區域表面溫度都在1000℃左右，因此材料屬性采取Q460E鋼種在Gleeble-3800試驗機上的1000 ℃的各項熱物性參數，如表3所示。

由于連鑄坯在矯直區內弧側表面受拉，外弧側表面受壓，因此提取矯直區內弧側表面應變速率的計算值，如圖5所示。

表3 Q460E在1000 ℃時熱物性參數表

圖5 兩種機型曲線矯直應變速率對比Fig.5 Strain rate of two casting machines

傳統五點彎曲五點矯直機型曲線由于矯直段弧長比較短，矯直變形時間短，并且多點矯直存在應變速率突變，在最后一個矯直點的應變速率達到1.2×10-3s-1，而新的曲率正弦變化機型曲線由于矯直區很長，應變速率變化比較平緩，最大值都在10-5以下，可以看出，新的曲率變化符合正弦規律的機型曲線應變速率明顯小于原機型曲線應變速率。

新曲線由于圓弧段的大量減少，變形的時間比原曲線長很多，在矯直段，新曲線變形時間為350 s，原曲線變形時間為60 s。新曲線在矯直段有更長的應變時間，在這段時間連鑄坯會發生大量的蠕變變形，從而可以充分利用蠕變變形使鑄坯矯直。

4 蠕變試驗

對某鋼廠生產的Q460E連鑄坯取樣，其化學成分如表4所示，本次試驗采用Gleeble-3800熱/力模擬試驗機對連鑄坯Q460E的高溫力學性能和蠕變力學性能進行測試[16]。試件選取直徑10 mm、長度為120 mm兩端加工有螺紋的圓棒。

表4 Q460E的化學成分(質量分數)

為了更精確地模擬材料在連鑄過程中的力學性能，在模擬試驗機上采取了與工廠相同的熱循環制度。以10 ℃/s的速度加熱至1320 ℃，并且保溫2 min，然后以3 ℃/s的速度冷卻至1000 ℃，通過0.01 s-1恒定應變速率將試件拉斷得到應力應變曲線，從而確定Q460E鋼在1000 ℃的屈服強度為29.2 MPa。

圖6 蠕變試驗拉斷的試件Fig.6 Specimens after creep tensile tests

采用上述相同的熱循環制度，在溫度為1000 ℃的條件下，進行恒定應力拉伸試驗，應力分別取為18 MPa、19 MP、20 MPa、22 MPa，圖6所示為試件蠕變拉斷后的形狀。

蠕變數據的整理和處理方法參考日本學者平修二的方法，對蠕變曲線進行整理推導。金屬材料的蠕變曲線對于各種金屬都具有相同的形式，表示某一溫度和應力下蠕變的經驗公式為

ε=ε0+btn+Kt

(10)

式中，ε0為瞬時應變；b和K分別為應力和溫度相關系數；n為硬化指數。

式(10)中第二項表示過渡蠕變的應變分量，第三項表示穩態蠕變的應變分量。忽略瞬時應變，對原始蠕變曲線進行自定義函數擬合，擬合函數為

ε=btn+Kt

(11)

兩端取對數得

ln(ε-Kt)=lnb+nlnt

(12)

線性擬合后蠕變本構方程為

εc=exp(0.124 26T-168.3733)σ10t0.36+exp(0.044 36T-88.749 92)σ10t

(13)

式中，εc為蠕變應變；σ為應力，MPa；T為溫度，℃。

式(13)揭示了應力與溫度對Q460E蠕變的影響規律。把蠕變試驗下1000 ℃對應的應力18 MPa、19 MP、20 MPa、22 MPa分別帶入蠕變方程，得到理論值，再與試驗值做比較，如圖7所示。蠕變方程與試驗值較吻合，由于整體連鑄生產過程的時間相對試驗時間比較短，多為2000 s左右，蠕變變形基本發生在過渡蠕變和穩定蠕變階段，所以蠕變方程式(13)完全可以適用于連鑄生產中的蠕變變形研究。

圖7 蠕變方程計算值與試驗值對比圖Fig.7 Comparative data by creep test and creep equation

(14)

由式(14)可知，等號右邊第一項隨著時間的延長，蠕變應變速率逐漸減小，最終趨近于第二項的最小蠕變應變速率。

當連鑄坯溫度為1000 ℃時，采用屈服應力29.2MPa代入式(14)，得到1000 ℃下最小蠕變應變速率為2.374×10-5s-1，對比曲率正弦變化機型曲線的連鑄坯應變速率和五點彎曲五點矯直機型曲線的應變速率可以看出：

曲率正弦變化的機型曲線使連鑄坯發生矯直變形的應變速率普遍較小，集中在10-5s-1，接近最小蠕變應變速率；而五點彎曲五點矯直機型曲線在矯直區的應變速率都較大，最大值接近10-3s-1，遠大于蠕變應變速率，說明新設計的機型曲線使連鑄坯在矯直變形中更多地依靠低于屈服強度作用的蠕變變形，而五點彎曲五點矯直機型曲線則更多依靠大于屈服強度的塑性變形，這必然導致應變速率的增大，也增加了裂紋出現的可能。

5 結論

(1)新機型曲線顯著延長了連鑄機彎曲段和矯直段弧長，縮短基本圓弧段弧長，并且具有整體鑄機高度較低、矯直段應變速率小、蠕變變形量大的特點，充分發揮了材料的高溫蠕變特性，使鑄坯發生變形。

(2)新曲線的應變速率遠小于五點彎曲五點矯直機型曲線的應變速率。新設計的機型曲線使連鑄坯在矯直變形中更多地依靠低于屈服強度作用的蠕變變形，而五點彎曲五點矯直機型曲線則更多地依靠大于屈服強度的塑性變形。

在以后的鑄機曲線設計中可以參考利用蠕變進行矯直的新方法，進一步縮短基本圓弧段弧長，甚至取消基本圓弧段，最大限度延長矯直段弧長，降低應變速率，從而達到完全的蠕變矯直，大大降低鑄坯的矯直裂紋發生率，提高鑄坯質量。

[1]TOMONOH.DevelopmentofSteelContinuousCastinginJapan:HasBessemer’sDreamComeTrue?[J].Ironmaking&Steelmaking，2015，42(4)：242-251.

[2] 殷瑞鈺.中國連鑄的快速發展[J].鋼鐵，2004， 39(z1)：1-7.YINRuiyu.RapidDevelopmentofSteelContinuousCastinginChina[J].IronandSteel，2004，39(z1)：1-7.

[3]DUFengming，WANGXudong，LIUYu，etal.InvestigationonThermo-mechanicalBehaviorofMoldCornerforContinuousCastingSlab[J].ISIJInternational，2015，55(10)：2150-2157.

[4]BRIMACOMBEJK，SORIMACHIK.CrackFormationintheContinuousCastingofSteel[J].Metallurgical&MaterialsTransactionsB，1977，8(2)：489-505.

[5]GRILLA，SCHWERDTFEGERK.Finite-elementAnalysisofBulgingProducedbyCreepinContinuouslyCastSteelSlabs[J].Ironmaking&Steelmaking，1979，6(3)：131-135.

[6]OKAMURAK，KAWASHIMAH.Three-dimensionalElasto-plasticandCreepAnalysisofBulginginContinuouslyCastSlabs[J].ISIJInternational，1989， 29(8)：666-672.

[7]HUESPEAE，CARDONAA，NIGRON，etal.Visco-plasticConstitutiveModelsofSteelatHighTemperature[J].JournalofMaterialsProcessingTechnology， 2000，102(1/3)：143-152.

[8] 李憲奎.具有兩個光滑連續矯直區的低矮型連鑄機[J].鋼鐵，1996，31(4)：31-35.LIXiankui.Low-headContinuousCastingMachinewithTwoSmoothContinuousStraighteningAreas[J].IronandSteel，1996，31(4)：31-35.

[9] 滿媛,李憲奎,楊拉道.連鑄板坯連續矯直過程充分利用鋼高溫特性的研究[J].塑性工程學報，2008， 15(6)：96-101.MANYuan，LIXiankui，YANGLadao.StudyaboutUsingtheElevatedTemperatureCharacteristicsofSteelduringContinuousStraightening[J].JournalofPlasticityEngineering，2008，15(6)：96-101.

[10] 馬春武，封偉華，儲鴻文. 連鑄坯彎曲矯直時的變形行為[J]. 鋼鐵研究學報，2012，24(3)：21-27.MAChunwu，FENGWeihua，CHUHongwen.DeformationBehaviorduringBendingorStraighteningofSlab[J].JournalofIronandSteelResearch，2012，24(3)：21-27.

[11] 景奉儒，李憲奎，楊拉道，等. 直弧型板坯連鑄機連續彎曲矯直曲線的優化研究[J]. 鋼鐵，2009，44(4)：23-27.JINGFengru，LIXiankui，YANGLadao，etal.OptimizationofContinuousBendingandStraighteningCurveofVerticalArcSlabCaster[J].IronandSteel，2009，44(4)：23-27.

[12] 黃文, 張卓然, 張興中,等.連鑄機多點矯直的矯直輥反力的解析計算法[J].特種鑄造及有色合金， 2015，35(11)：1139-1142.HUANGWen，ZHANGZhuoran，ZHANGXingzhong，etal.AnalyticalSolutionofRollerReactingForcesinMultipointStraighteningofContinuousCaster[J].SpecialCasting&NonferrousAlloys，2015，35(11)：1139-1142.

[13] 李寧.連續矯直在薄板坯連鑄中的應用及其矯直力計算[J].重型機械，2005(1)：26-30.LINing.TheApplicationofContinuousStraighteninginCSPandtheCalculationofStraighteningForce[J].HeavyMachine，2005(1)：26-30.

[14] 曹廣疇.現代板坯連鑄[M].北京：冶金工業出版社，1994：102-103.CAOGuangchou.ModernContinuousCastingforSteelSlab[M].Beijing：MetallurgicalIndustryPress, 1994：102-103.

[15]BZVNEKZM，DIERBERGERJ.SomeProblemsofBridgeContactAnalysisUsingMarc[J].ComputationalandExperimentalMethods，2003，38：63-72.

[16] 董志華，陳登福，龍木軍，等.20CrMnTi鋼連鑄坯柱狀晶區的高溫力學性能[J].材料研究學報，2013，27(3)：274-278.DONGZhihua,CHENDengfu,LONGMujun,etal.HighTemperatureMechanicalPropertiesfortheColumnarZoneofSteel20CrMnTi[J].ChineseJournalofMaterialsResearch，2013，27(3)：274-278.

(編輯 王旻玥)

New Straightening Technology of Continuous Casting Slabs Based on High-temperature Creep Properties

ZHANG Xingzhong GUO Long FENG Changxi

National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Yanshan University,Qinhuangdao,Hebei，066004

A new straightening technology where the continuous casting slabs might be straightened by full using of high-temperature creep properties was proposed based on the straightening technologies that widely used currently. The new straightening curves were designed herein where the curvatures were changed as sine law. The arc lengths of straightening segments and bending segments were extended significantly. The strain rate in the new curve was less than creep strain rate so that high-temperature creep behavior might be used fully in the straightening processes by finite element method. The parameters of thermo-physical property were confirmed and the creep constitutive equation was derived through the uniaxial tensile tests of Q460E steels on the Gleeble-3800 machine. Strain rates in the new curve were close to the minimum creep strain rates, thus the slabs might be straightened by creep deformations mainly. Due to the lower strain rates, internal cracks caused by bending and straightening might be effectively avoided, and the quality of the slabs was improved.

continuous casting slab; creep straightening; strain rate; straightening curve

2016-06-16

國家自然科學基金資助項目(51275446)；河北省自然科學基金資助項目(E2016203492)；河北省研究生創新資助項目(2016SJBS027)；河北省引進留學人員項目(C2013005012)

TF777.1；TF341.6

10.3969/j.issn.1004-132X.2017.10.016

張興中，男，1965年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心教授、博士研究生導師。主要研究方向為機械設計及理論和高效連鑄技術。獲省科技進步三等獎2項，發表論文50余篇。E-mail:Zhangxzh@ysu.edu.cn。郭 龍，男，1985年生。燕山大學機械工程學院博士研究生。馮常喜，男，1991年生。燕山大學機械工程學院碩士研究生。