談“奇數與偶數”的教學處理

徐國強

人教版小學數學五年級下冊中有如下問題（如圖所示）。該問題相對抽象，如何幫助學生理解和掌握相關結論？筆者在教學實踐中總結了如下經驗。

一、正確理解問題

題目是讓我們研究奇數、偶數相加時，和可能存在的規律。但題目的這種設問的方式可能給人一種錯覺。以“奇數與偶數的和是奇數還是偶數？”為例，它容易讓我們認為答案要么是奇數，要么是偶數。盡管最終答案的確是奇數，但這是研究的結果。研究之前，我們應認識到，這一問題的答案有三種可能———或者是奇數，或者是偶數，或者不確定。若先入為主地認為答案要么是奇數，要么是偶數，將會使我們的說理變得淺嘗輒止：既然正確答案或者是奇數，或者是偶數，我們只需用一個具體的例子試一下就行。比如，由1+2=3立即得到答案是奇數。如果正確理解了題目，我們面對1+2=3這個例子時，能得到的結論是：奇數加偶數，其和或者是奇數，或者不確定。

二、多角度說理

要真正理解上述結論，多角度說理是不可或缺的。常見的方式有如下幾種。

1.不完全歸納。這是通過列舉有限的例子得出結論的說理方式。比如，為了研究奇數與偶數的和的奇偶性，我們通過研究1+2，3+8，9+24等發現其結果均是奇數，從而得出結論：奇數+偶數=奇數。用不完全歸納法得到結論后，要引導學生認識到這種方法的局限性：例是舉不完的。我們通過對有限幾個例子的考察，發現考察的對象都滿足某一規律，其實并沒有充分的理由確定所有的對象都滿足這一規律。對這種方式的局限性的認識，是進一步考慮其他說理方式的基礎。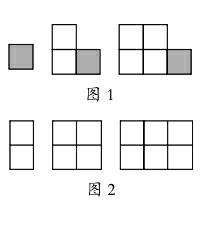

2.以形說數。我們以圖1中的圖形表示奇數，用圖2中的圖形表示偶數。顯然，一個表示奇數的圖形和一個表示偶數的圖形拼在一起，還是一個表示奇數的圖形，從而得到“奇數+偶數=奇數”。其他的情形類似。

3.運動變化。考慮一個人游泳，橫渡一條小河。顯然，他橫渡小河一次到了對岸，再橫渡一次，又回到了出發的地方。進一步，橫渡小河奇數次，到了對岸，橫渡小河偶數次，回到了出發的地方。考慮奇數+偶數，相當于先橫渡奇數次，再橫渡偶數次，即先到對岸，再橫渡偶數次，顯然還在對岸，相當于橫渡奇數次。于是奇數+偶數=奇數。考慮運動與變化還容易理解一個更一般的結論：由于在運動變化中，偶數往往意味著不變，因此，一個數加上偶數，不改變奇偶性。

三、聯系與推廣

1.加強聯系。以下三個結論：奇數+奇數=偶數，奇數+偶數=奇數，偶數+偶數=偶數，可以通過“奇數+1=偶數，偶數+1=奇數”建立起聯系。比如，知道“偶數+偶數=偶數”，那么，奇數+偶數=偶數+1+偶數=偶數+偶數+1=偶數+1=奇數，這就在“偶數+偶數=偶數”與“奇數+偶數=奇數”之間建立起了聯系。其他的情形類似。

2.適當推廣。推廣的方向主要有兩個，一是從兩個到多個。得到奇數個奇數的和是奇數，偶數個奇數的和是偶數。進一步，在一個加法算式中，如果奇數的個數是奇數個，則和為奇數；如果奇數的個數為偶數個，則和為偶數。二是由加法推廣到乘法。得到奇數×奇數=奇數，奇數×偶數=偶數，偶數×偶數=偶數。進一步，在一個乘法算式中，只要存在偶數，結果就是偶數，否則，結果就是奇數。

（作者單位：寧鄉縣老糧倉鎮中心小學）