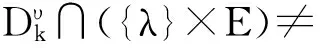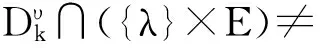Existence of Positive Solutions and Multiple Results for Nonlinear Eigenvalue Problems on Time Scales
LU Haixia
(School of Arts and Science, Suqian College, Suqian 223800, Jiangsu)
Existence of Positive Solutions and Multiple Results for Nonlinear Eigenvalue Problems on Time Scales
LU Haixia
(SchoolofArtsandScience,SuqianCollege,Suqian223800,Jiangsu)
In this paper, we discuss the nonlinear eigenvalue problem on time scalesT
eigenvalue problems; time scales; global bifurcation; positive solutions
1 Introduction
In this paper, we study the following nonlinear eigenvalue problem on time scales
(1)
where λ is a positive parameter, andTis a closed subset of the interval [0,1] with 0,1∈T.
The concept of time scales was created by Hilger[1]in order to unify continuous and discrete calculus. Some other early papers in this area include Agarwal and Bohner[2], Aulbach and Hilger[3]and Erbe and Hilger[4]. In recent years, much research has been done for the existence of solutions of boundary value problems on time scales by Krasnoselskii fixed point theorems, Leggett-williams theorem, upper and lower solution method and so on(see [5-14]). By using the global bifurcation theory and the results in [16], Luo and Ma[15]obtained the existence of solutions of the nonlinear eigenvalue problem (1) in the case that the nonlinear term f(u(t)) satisfied
sf(s)>0, ?s≠0.
(2)
Inthispaper,wediscussnonlineardifferentialequation(1)byusingRabinowitz’sbifurcationtheoremsfromboththetrivialsolutionandinfinity.Theexistenceofpositivesolutionsandmultiplicityofsolutionsof(1)areprovedinthecasethat(2)isnotsatisfied.Themethodandresultsinthispaperimprovethosegivenin[13-15].
2 Preliminaries
LetTbe a closed subset of the interval [0,1] with 0,1∈T. For completeness and convenience, we recall the following concepts related to the notation of the time scales.
Definition 2.1 Define the forward jump operator and backward jump operatorσ,ρ:T→Tby
σ(t)=inf{s∈T:s>t}, ρ(t)=sup{s∈T:s for anyt∈T. The pointt∈Tis said to be left-dense, left-scattered, right-dense, right-scattered ifρ(t)=t,ρ(t) We assume throughout that,σ(0)=0 andρ(1)=1. Definition 2.2 Letu:T→R andt∈T.uis said to be differentiable attif there exists a number, denoted byuΔ(t), with the property that for eachε>0 there is a neighborhoodU∈Toftsuch that |u(σ(t))-u(s)-uΔ(t)(σ(t)-s)|≤ε|σ(t)-s| foralls∈U. Ifuis differentiable at everyt∈Tthenuis said to be differentiable onT. The second derivative ofuattis defined to beuΔΔ(t):=(uΔ)Δ(t). We also define the functionuσ:=u°σ. Definition 2.3 A functionu:T→R is said to be rd-continuous onTif it is continuous at all right-dense points and has finite left-sided limit at each left-dense point inT. ‖u‖1=‖u‖+‖uΔ‖, LetX=C0(T), E={u∈C1(T)∶u(0)=u(1)=0}, Letφ(t), ψ(t)betheuniquesolutionoftheequationLu(t)=0onTsatisfyingtheboundaryconditions FromLemma3.3in[16],thereexistsaconstantω≠ 0suchthatω=ψ(t)φΔ(t)-φ(t)ψΔ(t)forallt∈T.For(s, t)∈T×T,let Theboundaryvalueproblem(1)isequivalenttothefollowingintegralequation (3) for some t0∈T.Thenu0≡0. Forconvenience,welistthefollowingconditionswhichwillbeusedinthispaper. (H4) There existsr>0 such thatf(r)<0 andf(-r)>0. Letζ,ξ∈C(R, R) satisfy f(s)=f0s+ζ(s), f(s)=f∞s+ξ(s). By the conditions (H2) and (H3), we have (4) Now (1) can be rewritten in the form either Lu=λ f0uσ+λζ(uσ), (5) or Lu=λ f∞uσ+λξ(uσ). (6) Definition 2.4 Suppose thatu∈C1(T) andt∈T. Ifu(t)=0, thentis a zero ofu. Ifu(t)=0 anduΔ(t)≠ 0, thentis a simple zero ofu. Ifu(t)uΔ(t)<0 (and henceσ(t)>t), then we say thatuhas a generalized zero at the point Simple zeross∈Tand generalized zeross?T, as defined above, are often referred to as simple generalized zeros. (i) the only zeros ofuinTare simple; (ii)uhas exactlyk-1 simple generalized zeros in (0, 1); (iii) ±uΔ(0)>0. Letλkbe thekth eigenvalue of the linear eigenvalue problem It is known from [16, Lemma 5.1] and [17, Lemma 2.6] that 0<λ1<λ2<λ3<…, uk∈Sk, k=1, 2, 3,…, and eachλkhas algebraic multiplicity one. LetΓdenote the closure of the set of nontrivial solutions of (3) in R×E. A continuum ofΓis a maximal closed connected subset. Hσ=GEζσ:R×E→E. We see from (3) and (5) that finding a solution (λ,u)∈Γis equivalent to finding a solution (λ,u)∈R×Eof the equation It follows from the definition ofHσthatHσis compact and continuous. In addition, it follows from (4) thatHσ(λ,u)=°(|u|) forunear zero, uniformly on boundedλintervals. Therefore, following the arguments in the proof of Theorem 7.1 in [16] Lemma 2.2 holds. Fσ=GEξσ: R×E→E. We see from (6) that (3) is equivalent to the following equation (7) ItfollowsfromthedefinitionofFσthatFσiscompactandcontinuous.Andby(4)wehavethatFσ(λ,u)=°(|u|)forunear∞,uniformlyonboundedλintervals.Hence(7)isoftheformdiscussedin[18]. Let Г1denotetheclosureofthesetofnontrivialsolutionsof(3)inR×X. Obviously, from the point of the set, Г=Г1. Hence, in the sense of the set, we denoteΓandΓ1byΓ. Lemma 2.4[14, 19]LetMbe a subset ofΓ. Then (i)Mis a closed set in R×XiffMis a closed set in R×E; (ii)Mis a connected component set in R×XiffMis a connected component set in R×E; (iii)Mis a unbounded set in R×XiffMis a unbounded set in R×E. In this section we give our main results. Theorem 3.1 Let (H1)-(H3) hold. Assume for some integerk≥1, one of the following conditions is satisfied: Then (1) has two solutionsu+kandu-ksuch thatu+khas exactlyk-1 simple generalized zeros inTwith (u+k)Δ(0)>0,u-khas exactlyk-1 simple generalized zeros inTwith (u-k)Δ(0)<0. Theorem 3.2 Let (H1)-(H3) hold. Suppose that there exist two integersk≥ 1 andj≥0 such that one of the following conditions is satisfied: λAu≠u, ?λ>0,u∈?Br, (8)whereAisdenotedby(3), Br={u∈X| ‖u‖ Otherwise,thereexistλ0>0andu0∈?Brsuchthatu0=λ0Au0.Since‖u0‖=r,thenthereexistst0∈Tsuchthatu0(σ(t0))=r (theproofforu0(σ(t0))=-rissimilar). Butitfollowsfrom(H4)that Lu0(t0)=λ0f(u0(σ(t0)))=λ0f(r)<0, whichisacontradiction. Then [1] HILGER S. Analysis on measure chains-a unified approach to continuous and disrete calculus[J]. Results Math,1990,18(1):18-56. [2] AGARWAL R P, BOHNER M. Basic calculus on time scales and some of its applications[J]. Results Math,1999,35(1):3-22. [3] AULBACH B, HILGER S. Linear Dynamic Processes with in Homogeneous Time Scale, Nonlinear Dynamics and Quantum Dynamical System[M]. Berlin:Akademic Verlag,1990. [4] ERBE L H, HILGER S. Sturmian theory on measure chains[J]. Differential Equations Dynam System,1993,1(3):223-246. [5] AGARWAL R P, O'REGAN D. Nonlinear boundary value problem on a measure chain[J]. Nonlinear Anal,2001,44(4):527-535. [6] ANDERSON D R. Eigenvalue intervals for a two-point boundary value problem on a measure chain[J]. J Comput Appl Math,2002,141(1/2):57-64. [7] CHEN H H, CHEN C. Positive solutions for eigenvalue problems on a measure chain[J]. Nonlinear Anal,2002,51(3):499-507. [8] CHYAN C J, HENDERSON J. Eigenvalue problems for differential equations on a measure chain[J]. J Math Anal Appl,2000,245(2):547-559. [9] CHYAN C J, HENDERSON J. Twin solutions of boundary value problems for differential equations on a measure chain[J]. J Comput Appl Math,2002,141(1/2):123-131. [10] ERBE L H, PETERSON A. Positive solutions for a nonlinear differential equation on a measure chain[J]. Math Comput Modelling,2000,32(5/6):571-585. [11] ERBE L H, PETERSON A, MATHSEN R. Existence, multiplicity and nonexistence of positive solutions to a differential equation on a measure chain[J]. J Comput Appl Math,2000,113(1/2):365-380. [12] LI W T, SUN H R. Multiple Positive solutions for nonlinear dynamic systems on a measure chain[J]. J Comput Appl Math,2004,162(2):421-430. [13] SONG C X. Positive solutions for first-order PBVPs on time scales[J]. Chin Quart J Math,2012,27(3):337-343. [14] LI H Y, DAI L M. Positive solutions for nonlinear differential equations with sign changing nonlinearity on a measure chain[J]. J Math,2012,32(1):9-16. [15] LUO H, MA R Y. Nodal solutions to nonlinear eigenvalue problems on time scales[J]. Nonlinear Anal,2006,65(4):773-784. [16] DAVIDSON F A, RYNNE B P. Global bifurcation on time scales[J]. J Math Anal Appl,2002,267(1):345-360. [17] DAVIDSON F A, RYNNE B P. Curves of positive solution of boundary value problems on time scales[J]. J Math Anal Appl,2004,300(2):491-504. [18] RABINOWITZ P H. On bifurcation from infinity[J]. J Differential Equations,1973,14(3):462-475. [19] CUI Y J, SUN J X, ZOU Yumei. Global bifurcation and multiple results for Sturm-Liouville problems[J]. J Comput Appl Math,2011,235(8):2185-2192. (編輯 陶志寧) 時標上非線性特征值問題正解的存在性和多解性 陸海霞 (宿遷學院 文理學院, 江蘇 宿遷 223800) 討論時標T上非線性特征值問題其中λ是正參數.運用全局分歧理論,研究在一定條件下上述特征值問題發自u=0和(或)u=∞非零解的連通分支,得到此特征值問題正解的存在性和多解性結果,推廣和改進了一些已有結果. 特征值問題; 時標; 全局分歧; 正解. O175.8 A 1001-8395(2017)03-0289-06 Foundation Items:This work is supported by the National Science Foundation of China (No. 11501260) and Natural Science Foundation of Suqian city(No. Z201444) 10.3969/j.issn.1001-8395.2017.03.002 Received date: 2016-05-25. whereλis a positive parameter. Using the global bifurcation theory, we study the continua of its nontrivial solutions bifurcating fromu=0 and/oru=∞ under some conditions. In addition, the existence of positive solutions and the multiplicity of solutions of this nonlinear eigenvalue problem are obtained. Our results generalize and improve some known results. 2010 MSC:34B15















3 Main results