半線性橢圓方程Neumann問題的無窮多解
何 勇, 徐 博
(重慶科技學院 數理學院, 重慶 401331)
半線性橢圓方程Neumann問題的無窮多解
何 勇, 徐 博
(重慶科技學院 數理學院, 重慶 401331)
假設Neumann邊值問題中非線性項是次線性的,利用Ekland變分原理,得到2列無窮多解.
Neumann問題; Ekland變分原理; 次線性; 振蕩; 極小極大方法
1 引言和主要結果
考慮下述Neumann邊值問題:
(1)

令非線性項f(x,t)是次線性的,即存在g∈Lr(Ω;R+),h∈Lq(Ω;R+)和α∈[0,1]使得
|f(x,t)|≤g(x)|t|α+h(x).
(2)
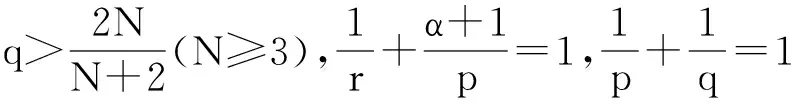
或者

定理 1 假設f(x,t)滿足(2)式,進一步假設
(3)
且
(4)
(I) 存在一列解(un),任意的un都是泛函φ的極小極大型臨界點,且當n→∞時,φ(un)→+∞;
推論 1 假設f(x,t)滿足(2)式,進一步假設
(5)
且
(6)
則有:
(I) 存在一列解(un),任意的un都是泛函φ的極小極大型臨界點,且當n→∞時,φ(un)→+∞;
注 1 文獻[12]在解決2點邊值問題時,考慮到了條件振蕩,且假設非線性項是有界的.本文的定理1給出了關于Neumann邊值問題的新的可解性條件.另一方面,存在泛函F(t,x)滿足定理1的條件但不滿足先前其它文獻中的假設.例如:令α=1/2和
其中j∈L1(Ω;R).
2 定理的證明
令H1(Ω)為有如下等價范數的Soblev空間
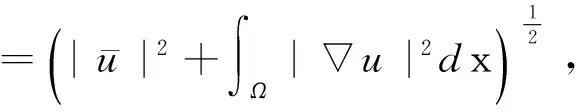

‖u‖L2≤C‖u‖, ‖u‖Lp≤C‖u‖,
其中u∈H1(Ω).
定義H1(Ω)上的泛函φ如下:

其中u∈H1(Ω).在次線性條件(2)下,泛函φ連續可微且在H1(Ω)上弱下半連續,而且有

其中u,v∈H1(Ω).眾所周知,當且僅當u是φ的臨界點時,u∈H1(Ω)是問題(1)的解.
φ(u)→+∞.
證明 由條件(2)和H?lder不等式有




令ε=1/4C2,有
其中C2、C3和C4是正常數.由條件(4)和上述引理得證.
定理1的證明 令
并定義



因此,由cn≥M和引理2,對于較大的n,

對于這樣的n,存在Sn上的序列(γk)使得當k→∞時
由文獻[14]的定理4.3知:存在H1(Ω)中的序列vk,使得當k→∞時有
φ(vk)→cn,
dist(vk,γk([0,1]))→0,
φ′(vk)→0.
現在,證明vk在H1(Ω)是有界的.對于足夠大的k有
且有wk∈γk([0,1])使得
‖vk-wk‖≤1.

此外




由此不等式和引理3有

因此得到定理1的(I)結論.
對于一個固定的n,定義H1(Ω)的子集Pn如下:

對于u∈Pn有
其中C8、C9和C10為正常數.從而得到φ在Pn中是有界的.
定義
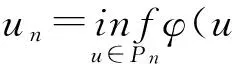
令(uk)是Pn上的極小化序列,即當k→∞時,
φ(uk)→un.
由上述不等式知:(uk)在H1(Ω)上有界,故uk中至少存在一個子列是有界的,仍記為uk.假設

因為φ是弱下半連續的,所以
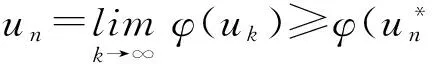





由引理2可得

定理1證畢.
[1] GUPTA C P. Perturbations of second order linear elliptic problems by unbounded nonlinearities[J]. Nonlinear Anal,1982,6(9):919-933.
[2] IANNACCI R, NKASHAMA M N. Nonliear boundary value problems at resonance[J]. Nonlinear Anal,1987,11(4):455-473.
[3] KUO C C. On the solvability of a nonliear second-order elliptic equations at resonance[J]. Proc Am Math Soc,1996,124(1):83-87.
[4] MAWHIN J. Semi-coercive monotone variational problems[J]. Acad Roy Belg Bull CI Sci,1987,73:118-130.
[5] MITREANU D, PAPAGEORGIOU N S. Existence and multiplicity of solutions for Neumann problems[J]. J Diff Eqns,2007,232(1):1-35.
[6] RABINOWITZ P H. On a class of functionals invariant under a Znaction[J]. Trans Am Math Soc,1988,310(1):303-311.
[7] TANG C L. Solvability of Neumann problem for elliptic equations at resonance[J]. Nonlinear Anal,2001,44(3):323-335.
[8] TANG C L. Some existence theorems for the sublinear Neumann boundary value problem[J]. Nonlinear Anal,2002,48(7):1003-1011.
[9] TANG C L. Multiple solutions of Neumann problem for elliptic equations[J]. Nonlinear Anal,2003,54(4):637-650.
[10] TANG C L, WU X P. Existence and multiplicity for solutions of Neumann problem for semilinear elliptic equations[J]. J Math Anal Appl,2003,288(2):660-670.
[11] TANG C L, WU X P. Multiple solutions of a class of Neumann problem for semilinear elliptic equations[J]. Nonlinear Anal,2005,62(62):455-465.
[12] HABETS P, MANASEVICH R, ZANOLIN F. A nonlinear boundary value problem with potential oscillating around the first eigenvalue[J]. J Diff Eqns,1995,117(2):428-445.
[13] EVANS L C. Partial Differential Equations[M]. Providence:Am Math Soc,1998.
[14] MAWHIN J, WILLEM M. Critical point theory and Hamiltonian systems[C]//Appl Math Sci, 74. New York:Springer-Verlag,1989.
[15] 頓調霞,李永祥. 一類三階微分方程的兩點邊值問題的正解[J]. 四川師范大學學報(自然科學版),2014,37(6):810-813.
[16] 劉瑞寬. 一類奇異三階兩點邊值問題正解的存在性[J]. 四川師范大學學報(自然科學版),2014,37(4):482-486.
[17] 趙亮,李樹勇,張秀英,等. 一類含連續分布時滯的隨機Hopfiled神經網絡模型的幾乎必然指數穩定性和p階矩指數穩定性[J]. 四川師范大學學報(自然科學版),2013,36(3):1-5.
2010 MSC:35R10
(編輯 周 俊)
Infinitely Many Solutions of Neumann Problem for Semilinear Elliptic Equations
HE Yong, XU Bo
(DepartmentofMathematicsandPhysics,ChongqingUniversityofScienceandTechonology,Chongqing401331)
By applying Ekland’s variational principal, we get two sequences of solutions for the Neumann boundary value problem when the nonlinearity is sublinear.
Neumann problem; Ekeland’s variational principle; sublinear; oscillating; minimax methods
2016-05-13
重慶市教委科學技術研究項目(KJ1713339)
何 勇(1982—),男,講師,主要從事概率統計方向的研究,E-mail:heyongmath@163.com
O175.8
A
1001-8395(2017)03-0316-04
10.3969/j.issn.1001-8395.2017.03.007

