基于最大靈敏度的分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)

那景童,徐 馳

(1.大連交通大學(xué) 電氣信息學(xué)院，遼寧 大連 116028；2.北京化工大學(xué) 信息學(xué)院，北京 100029)

基于最大靈敏度的分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)

那景童1,徐 馳2

(1.大連交通大學(xué) 電氣信息學(xué)院，遼寧 大連 116028；2.北京化工大學(xué) 信息學(xué)院，北京 100029)

針對(duì)分?jǐn)?shù)階控制器設(shè)計(jì)參數(shù)整定復(fù)雜的問題，提出一種基于最大靈敏度的分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)方法。采用粒子群優(yōu)化算法對(duì)原系統(tǒng)模型進(jìn)行簡(jiǎn)化處理，根據(jù)內(nèi)模控制原理設(shè)計(jì)分?jǐn)?shù)階內(nèi)模控制器；僅通過一個(gè)可調(diào)參數(shù)，實(shí)現(xiàn)分?jǐn)?shù)階內(nèi)模控制器的快速整定；通過最大靈敏度指標(biāo)實(shí)現(xiàn)分?jǐn)?shù)階內(nèi)模控制器的魯棒整定。仿真結(jié)果表明具有良好的控制品質(zhì)及克服參數(shù)攝動(dòng)的魯棒性。

分?jǐn)?shù)階控制；模型簡(jiǎn)化；內(nèi)模控制；最大靈敏度

作為傳統(tǒng)整數(shù)階微積分的拓展，分?jǐn)?shù)階微積分在控制領(lǐng)域受到越來越多的關(guān)注，特別是在分?jǐn)?shù)階控制器設(shè)計(jì)與系統(tǒng)建模方面[1-2]。有關(guān)文獻(xiàn)指出，利用分?jǐn)?shù)階微積分描述實(shí)際系統(tǒng)可以得到更加準(zhǔn)確的系統(tǒng)模型，特別是對(duì)于熱工系統(tǒng)、粘彈性系統(tǒng)[3]。同時(shí)，對(duì)于分?jǐn)?shù)階模型，采用分?jǐn)?shù)階控制器能夠得到較傳統(tǒng)整數(shù)階控制器更好的控制性能，分?jǐn)?shù)階控制效果更加細(xì)膩[4]。20世紀(jì)末，podluny提出了分?jǐn)?shù)階PID控制器[5]，其一般格式記為PIαDβ。分?jǐn)?shù)階PIαDβ控制器與傳統(tǒng)PID控制器相比，多了兩個(gè)可調(diào)參數(shù)(α,β)，當(dāng)α=β=1時(shí)，控制器屬于常規(guī)PID控制器，由于α,β連續(xù)可調(diào)，因此分?jǐn)?shù)階PIαDβ控制器具有更大的調(diào)節(jié)范圍、更強(qiáng)的魯棒性，為得到更優(yōu)的系統(tǒng)動(dòng)態(tài)性能創(chuàng)造了條件。但正是可調(diào)參數(shù)的增加增大了控制器參數(shù)的整定難度，文獻(xiàn)[6]提出基于控制系統(tǒng)期望帶寬的IMC-PIαDβ控制器，通過引入內(nèi)模控制準(zhǔn)則減少了分?jǐn)?shù)階控制器的整定參數(shù)，但該方法設(shè)計(jì)過程中未考慮控制模型參數(shù)變化的情況，需要分析系統(tǒng)的頻率響應(yīng)特性；當(dāng)系統(tǒng)工作環(huán)境發(fā)生變化時(shí)，控制器性能會(huì)急劇下降。

針對(duì)上述問題，采用粒子群優(yōu)化算法對(duì)原被控模型進(jìn)行簡(jiǎn)化，在簡(jiǎn)化模型的基礎(chǔ)上將內(nèi)模控制思想引入到分?jǐn)?shù)階控制器設(shè)計(jì)中，利用內(nèi)模控制原理有效減少分?jǐn)?shù)階控制器參數(shù)的整定，并基于最大靈敏度指標(biāo)實(shí)現(xiàn)了控制器的魯棒整定。

1 系統(tǒng)模型簡(jiǎn)化和分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)

1.1 系統(tǒng)模型簡(jiǎn)化

文獻(xiàn)[7]針對(duì)分?jǐn)?shù)階微分算子，采用改進(jìn)的Oustaloup濾波器進(jìn)行有理傳遞函數(shù)逼近，得到高階整數(shù)階模型，這使得系統(tǒng)控制器的設(shè)計(jì)變得更加復(fù)雜，所以針對(duì)分?jǐn)?shù)階系統(tǒng)進(jìn)行模型簡(jiǎn)化是很有必要的。在模型簡(jiǎn)化過程中大部分分?jǐn)?shù)階模型都可以用式(1)模型結(jié)構(gòu)進(jìn)行逼近：

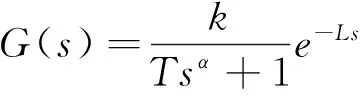
(1)

粒子群優(yōu)化(PSO)算法[8]具有較強(qiáng)的全局搜索能力和魯棒性且不需要目標(biāo)函數(shù)的特征信息，因此本文采用PSO算法進(jìn)行模型簡(jiǎn)化處理。其模型簡(jiǎn)化的具體步驟如下：

(1)選取目標(biāo)函數(shù)。本文所選目標(biāo)函數(shù)為原系統(tǒng)模型和簡(jiǎn)化模型的單位階躍響應(yīng)誤差，即

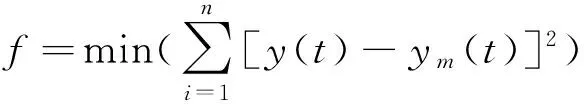
(2)

式中，n為搜索次數(shù)，y(t)和ym(t)分別為原系統(tǒng)模型和簡(jiǎn)化模型的單位階躍響應(yīng)。

(2)確定搜索參數(shù)向量并進(jìn)行初始化。本文選用簡(jiǎn)化模型結(jié)構(gòu)如式(1)，則搜索向量為θ=[k,T,α,L]，對(duì)待搜索參數(shù)進(jìn)行隨機(jī)初始化，并隨機(jī)產(chǎn)生粒子種群、學(xué)習(xí)因子。本文所選粒子種群為M=35，c1=c2=1.5。

(3)評(píng)價(jià)每個(gè)微粒的位置適應(yīng)值，計(jì)算其目標(biāo)函數(shù)。

(4)對(duì)于每個(gè)微粒，將其適應(yīng)值與微粒自身所經(jīng)歷過的最好位置(pbest)進(jìn)行比較，若更好，則將其替換為當(dāng)前的pbest。

(5)對(duì)于每個(gè)微粒，將其適應(yīng)值與整個(gè)群體所經(jīng)歷過的最好位置(gbest)進(jìn)行比較，若更好，則將其作為整個(gè)群體最優(yōu)位置。

(6)截止條件判斷，若符合截止條件則輸出搜索向量，否則返回步驟(3)。

1.2 分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)

內(nèi)模控制是將實(shí)際對(duì)象與對(duì)象模型相并聯(lián)，控制器取模型的動(dòng)態(tài)逆，從而滿足閉環(huán)系統(tǒng)性能，并通過添加低通濾波器來增強(qiáng)系統(tǒng)的魯棒性。內(nèi)模控制的結(jié)構(gòu)如圖1，其中R(s)、Y(s)、D(s)分別為設(shè)定值、系統(tǒng)輸出和外來擾動(dòng),U(s)為控制率，Gp(s)和GFo(s)分別為實(shí)際被控對(duì)象模型和簡(jiǎn)化模型。

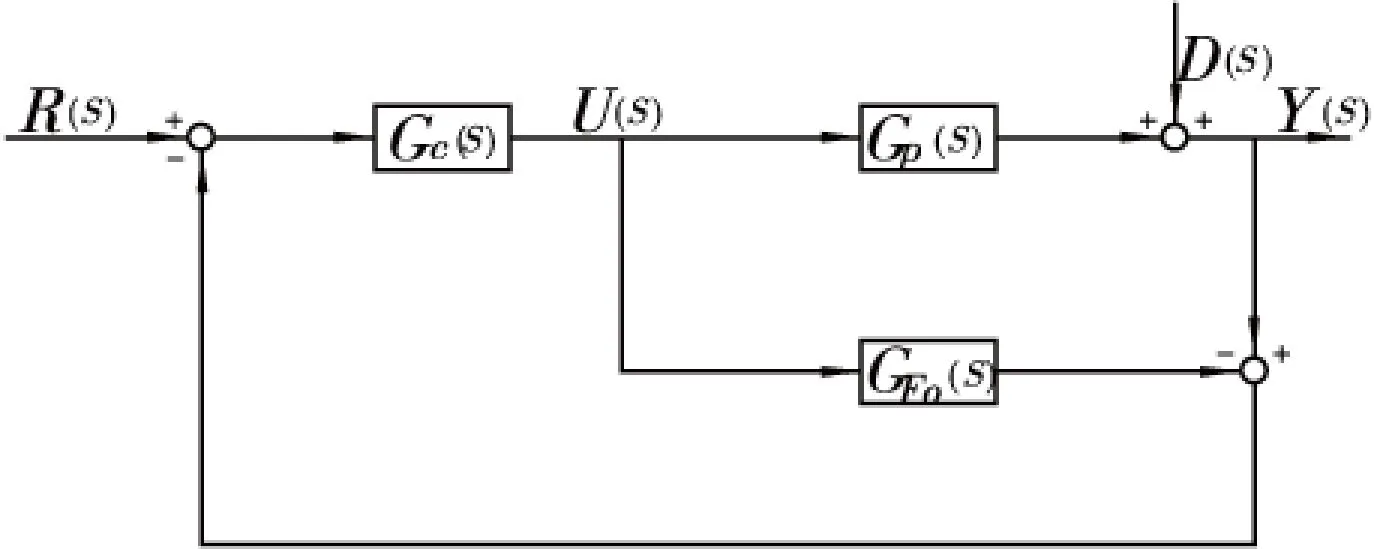
圖1 內(nèi)模控制框圖

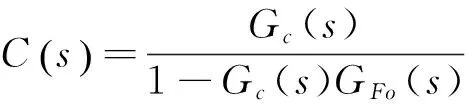
(3)

分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)與內(nèi)模控制類似，主要分為如下兩步：

(1)將簡(jiǎn)化模型分解成可逆和不可逆兩部分：

(4)

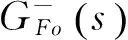
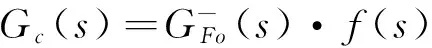
(5)

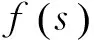
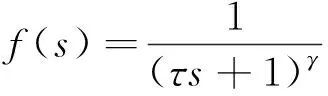
(6)

式中，γ是為了保證系統(tǒng)的物理可實(shí)現(xiàn)，τ為濾波器f(s)參數(shù)，也是內(nèi)模控制中唯一可調(diào)參數(shù)，減小τ系統(tǒng)動(dòng)態(tài)性能得到提高但魯棒性變差，增大τ情況正好相反。

2 基于最大靈敏度的分?jǐn)?shù)階內(nèi)模控制器參數(shù)整定

過程控制中，用于控制器設(shè)計(jì)的系統(tǒng)模型一般都不夠精確。因此，控制器的設(shè)計(jì)應(yīng)考慮對(duì)參數(shù)變化的魯棒性[9]。基于上述所提問題考慮，本文利用最大靈敏度Ms來設(shè)計(jì)FOIMC控制器(fractionalorderinternalmodelcontrol)。最大靈敏度定義為

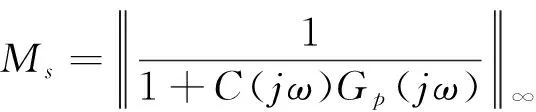
(7)式中，C(jω)Gp(jω)為系統(tǒng)開環(huán)傳遞函數(shù)，最大靈敏度是指系統(tǒng)開環(huán)傳遞函數(shù)的Nyquist曲線與臨界(-1,0)的最短距離的倒數(shù)，其幾何解釋如圖2。

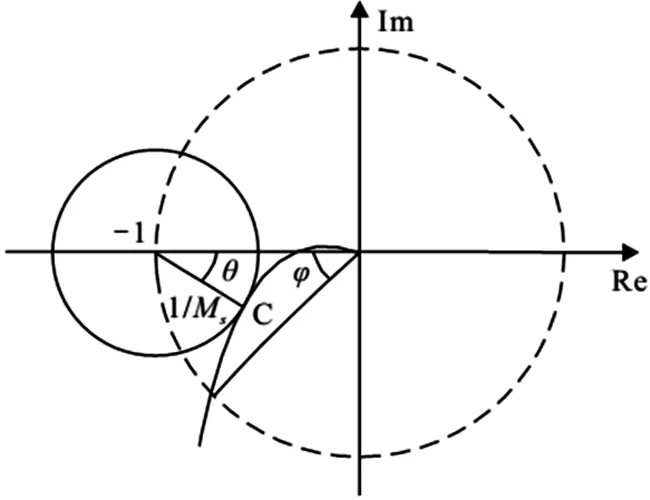
圖2 最大靈敏度幾何解釋

文獻(xiàn)[10]指出，Ms的取值范圍為1.1～2.5且Ms越小系統(tǒng)的魯棒性越強(qiáng)。如圖2，設(shè)相切點(diǎn)為C，則

Gl(jω)=C(jω)Gp(jω)。

(8)

在C點(diǎn)有：

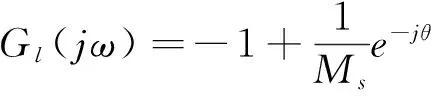
(9)

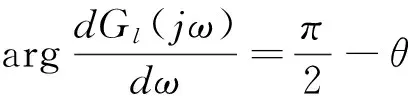
(10)

式中，θ為過臨界點(diǎn)與C點(diǎn)的直線與負(fù)實(shí)軸的夾角。若GFo(s)=Gp(s)，由式(3)可得系統(tǒng)的開環(huán)傳遞函數(shù)為：

(11)

令

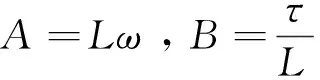
(12)

將式(11)代入到式(12)可得：

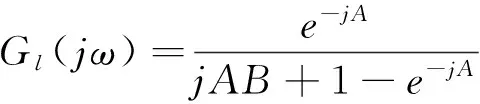
(13)

將式(13)代入到式(9)(10)，利用Matlab中fsolve函數(shù)求解可得到B與Ms的表達(dá)式：

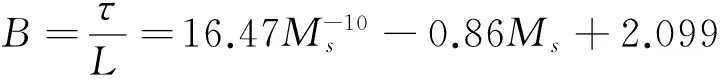
(14)

可得濾波器參數(shù)τ與Ms的關(guān)系式：

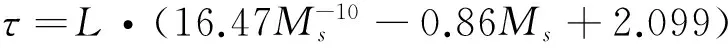
(15)

再由給定的Ms可以得到濾波器f(s)的時(shí)間常數(shù)τ。

3 仿真及結(jié)果分析

考慮分?jǐn)?shù)階被控對(duì)象[11-13]：

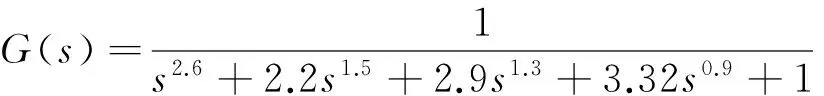
(16)

利用本文1.1節(jié)所提PSO優(yōu)化算法對(duì)式(16)進(jìn)行模型簡(jiǎn)化，優(yōu)化結(jié)果為

θ=[K,T,α,L]=[0.994 6,6.230 1,1.039 4,0.299 6]。

(17)

因此，可得式(16)的化簡(jiǎn)模型為

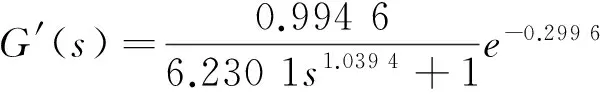
(18)

針對(duì)簡(jiǎn)化模型式(18)設(shè)計(jì)分?jǐn)?shù)階內(nèi)模控制器，這里取Ms=1.2，由本文2節(jié)控制器設(shè)計(jì)步驟可得分?jǐn)?shù)階內(nèi)模控制器為：

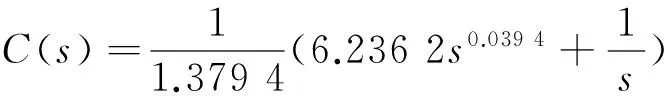
(19)

文獻(xiàn)[11]針對(duì)式(18)給出了最優(yōu)分?jǐn)?shù)階PID控制器為：

(20)

文獻(xiàn)[12]針對(duì)式(16)給出的一種分?jǐn)?shù)階內(nèi)模PID控制器為：

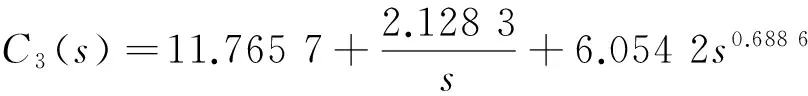
(21)

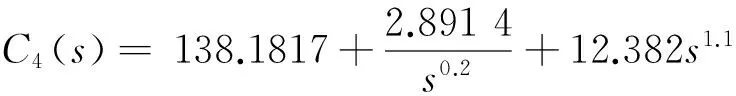
(22)

分別采用本文方法，文獻(xiàn)[11-13]方法得到系統(tǒng)的單位階躍響應(yīng)如圖3。

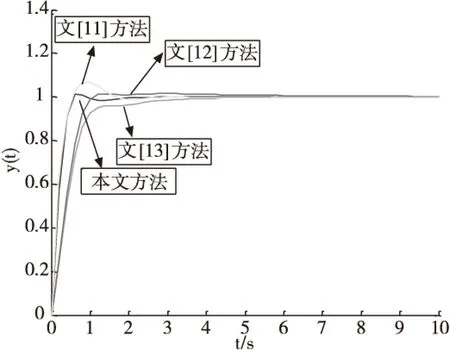
圖3 系統(tǒng)單位階躍響應(yīng)對(duì)比

從圖3可得，本文設(shè)計(jì)的分?jǐn)?shù)階內(nèi)模控制器相比文獻(xiàn)[11-13]所提控制器具有上升時(shí)間短、穩(wěn)態(tài)誤差小、存在微小超調(diào)，綜合考慮本文所提分?jǐn)?shù)階內(nèi)模控制器具有良好的控制品質(zhì)。

當(dāng)系統(tǒng)參數(shù)發(fā)生變化時(shí)，即：

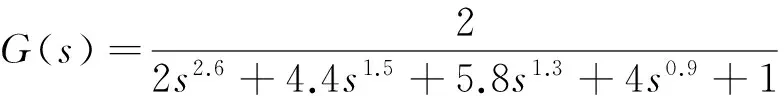
(23)

此時(shí)，系統(tǒng)單位階躍響應(yīng)如圖4。為了有效說明本文所提控制器具有更好的控制品質(zhì)和魯棒性，本文選取閉環(huán)系統(tǒng)的超調(diào)量δ%、調(diào)節(jié)時(shí)間、絕對(duì)時(shí)間誤差積分ITAE作為驗(yàn)證系統(tǒng)控制品質(zhì)的指標(biāo)，見表1。由圖3、4和表1可得，本文方法與文獻(xiàn)[11-13]方法相比，都存在微小超調(diào)，綜合考慮本文所提控制器在動(dòng)態(tài)響應(yīng)和魯棒性方面均具有一定優(yōu)勢(shì)。

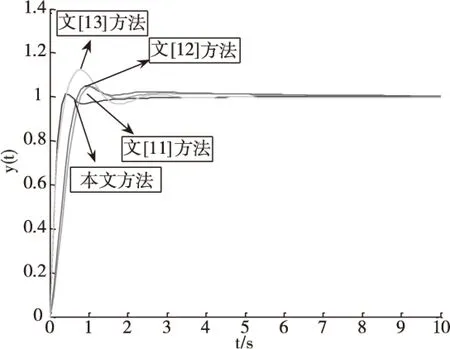
圖4 模型失配時(shí)系統(tǒng)的單位階躍響應(yīng)對(duì)比

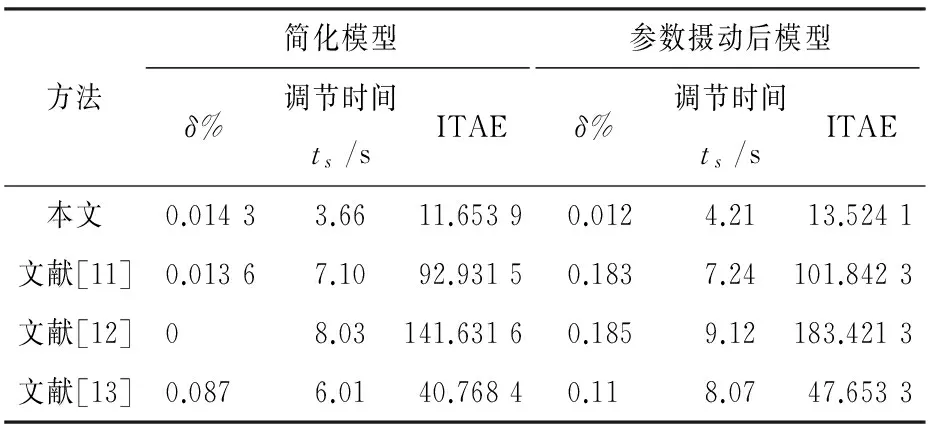
方法簡(jiǎn)化模型參數(shù)攝動(dòng)后模型δ%調(diào)節(jié)時(shí)間ts/sITAEδ%調(diào)節(jié)時(shí)間ts/sITAE本文0.01433.6611.65390.0124.2113.5241文獻(xiàn)[11]0.01367.1092.93150.1837.24101.8423文獻(xiàn)[12]08.03141.63160.1859.12183.4213文獻(xiàn)[13]0.0876.0140.76840.118.0747.6533

4 結(jié) 論

本文針對(duì)以往分?jǐn)?shù)階控制器參數(shù)整定復(fù)雜問題，提出一種基于最大靈敏度的分?jǐn)?shù)階內(nèi)模控制器設(shè)計(jì)方案。利用PSO算法對(duì)原系統(tǒng)模型進(jìn)行簡(jiǎn)化處理，然后將內(nèi)模控制思想引入到簡(jiǎn)化模型中設(shè)計(jì)分?jǐn)?shù)階內(nèi)模控制器，所得控制器僅有一個(gè)可調(diào)參數(shù)，再通過靈敏度指標(biāo)Ms推導(dǎo)出控制器唯一

參數(shù)的數(shù)學(xué)表達(dá)式。仿真結(jié)果說明文章所提方法是行之有效的。

[1]OLDHAMKB,SPANIERJ.Thefractionalcalculus[J].MathematicalGazette,1974,56(247):396-400.

[2] 朱呈祥, 鄒云. 分?jǐn)?shù)階控制研究綜述[J]. 控制與決策，2009，24(2):161-169.

[3]CAPONETTOR.Fractionalordersystems:Modelingandcontrolapplications[M].Singapore:WorldScientific,2010:1-4.

[4]MALEKH,LUOY,CHENYQ.Identificationandtuningfractionalorderproportion-integralcontrollersfortimedelayedsystemswithafractionalpole[J].Mechatronics, 2013, 23(7): 746-754.

[5]PODLUBNYI.Fractional-ordersystemsandPIDcontrollers[J].IEEETransonAutomatiControl, 1999,44(1): 208-214.

[6]LiDZ,FANWF,JINQB,etal.AnIMC-PIλDμcontrollerdesignforfractionalcalculussystem[C].Procofthe29thChineseControlConf.Beijing:IEEE, 2010:3581-3585.

[7] 薛定宇. 控制數(shù)學(xué)問題的MATLAB求解[M]. 北京: 清華大學(xué)出版社，2007．

[8]BIRGE,B.Aparticleswarmoptimizationtoolboxformatlab[Z].IEEESwarmIntelligenceSymposiumProceedings,2003,April:24-26.

[9]KAYAI.Two-degree-of-freedomIMCstructureandcontrollerdesignforintegratingprocessesbasedongainandphase-marginspecifications[C]∥IEEEProcofControlTheoryandApplications.NewYork:IET, 2004, 151(4): 481-487.

[10]JINQB,LIUQ,WANGQ,etal.PIDcontrollerdesignbasedonthetimedomaininformationofrobustimccontrollerusingmaximumsensitivity[J].ChineseJournalofChemicalEngineering, 2013, 21(5): 529-536.

[11]DASS,PANI,DASS,etal.Improvedmodelreductionandtuningoffractional-orderPIλDμcontrollersforanalyticalruleextractionwithgeneticprogramming[J].ISATrans, 2012, 51(2): 237-261.

[12] 趙志誠，張博，劉志遠(yuǎn),等. 一種分?jǐn)?shù)階系統(tǒng)內(nèi)模PID控制器設(shè)計(jì)方法[J]. 信息與控制，2014,43(2):129-133.

[13] 李大字，劉展，曹嬌．2007 儀表自動(dòng)化及先進(jìn)集成技術(shù)大會(huì)論文集:基于IMC方法的分?jǐn)?shù)階系統(tǒng)控制器設(shè)計(jì)[C].北京: 儀器儀表學(xué)報(bào)雜志社，2007: 362-365．

(責(zé)任編輯 趙環(huán)宇)

A Design of Fractional Order Internal Model Controller Based on Maximum Sensitivity

NA Jing-tong1, XU Chi2

(1.School of Electrical Information, Dalian Jiaotong University, Dalian Liaoning 116028, China;2.School of Information, Beijing University of Chemical Technology, Beijing 100029, China)

With respect to the complexity of fractional order controller parameters tuning, a scheme of maximum sensitivity based fractional order internal controller is proposed. Firstly, the original model is simplified by using particle swam optimization (PSO) algorithm. Secondly, a fractional order controller is designed according to the principle of the internal model control (IMC) based on the simplified model. The proposed controller has only one adjustable parameter, through which the rapid tuning can be achieved. Finally, the robust tuning of the controller parameter is realized using maximum sensitivity index. Simulation results show that this method has good control quality and robustness.

fractional order control; model simplified; internal model control; maximum sensitivity

2016-09-18；最后

2016-11-14

那景童(1989-)，男，遼寧大連人，大連交通大學(xué)電氣信息學(xué)院碩士研究生，主要從事分?jǐn)?shù)階控制研究。

2096-1383(2017)03-0227-04

TP273

A