基于板殼理論的梁板結構導荷方式
高 揚
(上海市政工程設計研究總院(集團)有限公司,上海 200092)
?
基于板殼理論的梁板結構導荷方式
高 揚
(上海市政工程設計研究總院(集團)有限公司,上海 200092)
從板殼理論出發,首先計算了板撓度曲面的理論解,而后從梁的變形反推被導算到梁上的荷載,并以導荷函數的形式進行了描述,通過研究導荷函數的性質,清楚的反映了矩形板的平面尺寸及梁與板的剛度關系對結構導荷方式的影響。
梁板結構,矩形板,導荷方式,導荷函數,板殼理論
梁板結構在承受豎向荷載作用時,板上荷載的導算方式是結構設計分析中的一個基本問題。現有的研究多停留于有限元模擬階段[1,2],很難揭示更為本質的機理。從工程角度來講,一般結構所用的板(包括所謂的厚板結構)其厚度往往遠小于平面尺寸,在板殼理論[3]中均屬于“薄板”的概念,應當存在一個統一的表達式來描述荷載的傳導方式。本文針對特定邊界條件下的矩形梁板結構進行分析,根據板撓度曲面的解析解反推梁上所導算到的荷載,并用導荷函數的形式表示,通過研究導荷函數的性質來揭示板上荷載傳導的機理。
1 板的撓度曲面計算
1.1 撓度曲面方程與邊界條件
設矩形板邊長為a和b,厚度較之于平面尺寸是小量,板受均布面荷載q作用。考慮一種典型的約束情況,取對邊x=±a/2為簡支,對邊y=±b/2支承于彈性梁上,如圖1所示。
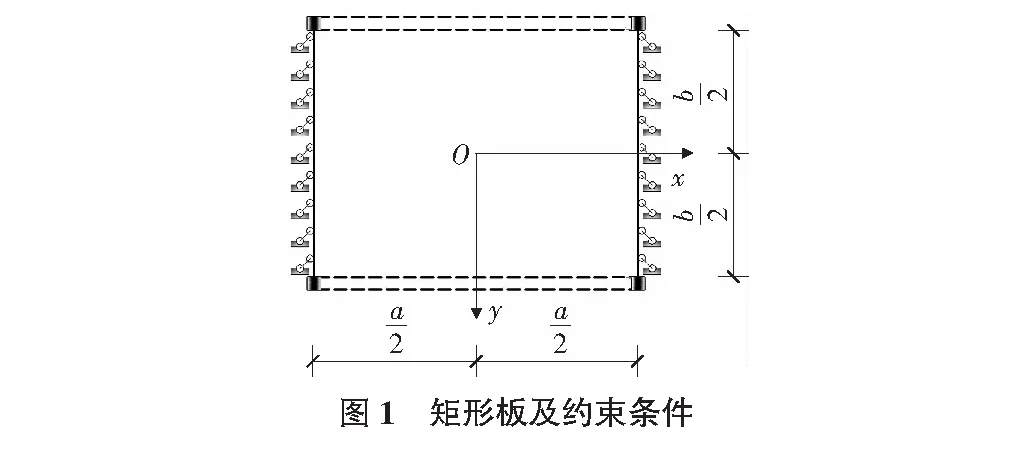
根據板殼理論,板的彎曲基本方程為:
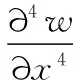
(1)
其中,w為板的撓度;D為板的彎曲剛度。
邊界條件為:
1)當x=±a/2時:
(2)
2)當y=±b/2時:
(3)
其中,v為板的泊松比;C為梁的彎曲剛度。邊界條件式(2)表示板在簡支端的撓度為0,且沿x方向不傳遞彎矩;邊界條件式(3)表示在彈性梁處,梁的扭矩、剪力分別與板在相應方向上的彎矩、剪力相平衡。
1.2 微分方程的解
微分方程(1)的解w包括特解w1和通解w2兩部分。根據結構的對稱性可取特解為:
(4)
同時由分離變量法給出通解的一般形式為:

(5)
因而微分方程(1)的解就可以表示為w1+w2:

(6)
其中,Am和Bm均為待定系數,由邊界條件確定。
將式(6)代入邊界條件,有:
1)當x=±a/2時,方程滿足邊界條件式(2)。
2)當y=±b/2時,由邊界條件式(3)可得到:
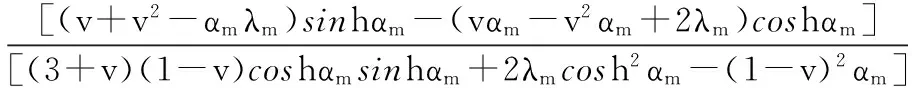
(7)
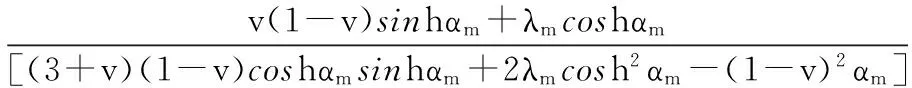
(8)
其中,αm為矩形板兩邊長度的比值,αm=mπb/(2a);λm為梁與板剛度的比值,λm=mπC/(aD)。將式(7),式(8)代入式(6),矩形板在給定邊界條件和豎向荷載下的撓度曲面w就確定了。
2 板的導荷方式分析
傳統的設計理念認為,彈性板上荷載近似以單向板對邊受力、雙向板梯形三角形傳力的方式全部傳遞給了梁[4]。如果用函數去描述這些導算到梁上的荷載,那么函數的形狀就能直觀地顯示出板在忽略面外剛度時的導荷方式。稱這樣的函數為導荷函數,下文將推導梁板結構在更為一般的情況下的導荷函數的表達式及相關性質。
2.1 導荷函數的推導
在y=±b/2處,梁的撓度為:
(9)
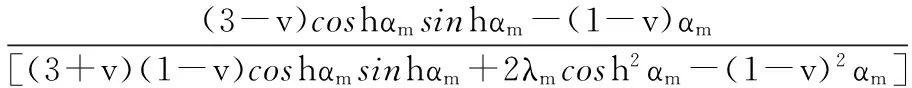
(10)
因而梁上被導算到的荷載qb(x)為:
(11)
導荷函數即為:
(12)
其物理意義為:梁在單獨承受導算荷載qb(x)=f(x)q下的內力變形和梁板協同承受面荷載q時梁的內力變形相等。進一步將導荷函數無量綱化得:

(13)
其中,φ為導荷函數的無量綱形式,φ=f/a;ξ為導荷函數的廣義坐標,ξ=x/a∈[-1/2,1/2]。
2.2 導荷函數的性質
由式(13)可得導荷函數φ(ξ)是一個無窮三角級數。φ(ξ)的形狀由級數各項φm的形狀及衰減速率決定。而控制這個速率的就是表征板平面尺寸的αm和表征梁板剛度關系的λm。
考察當λm較大,導荷函數式(13)可近似為:
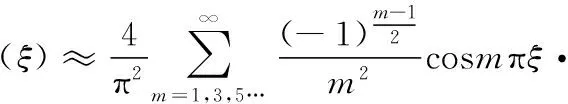
(14)
可將其表示為圖2的形式。其中第1項占有絕對重要的比重,高階項衰減極快,取很少的幾項之和就可足夠逼近級數的值。
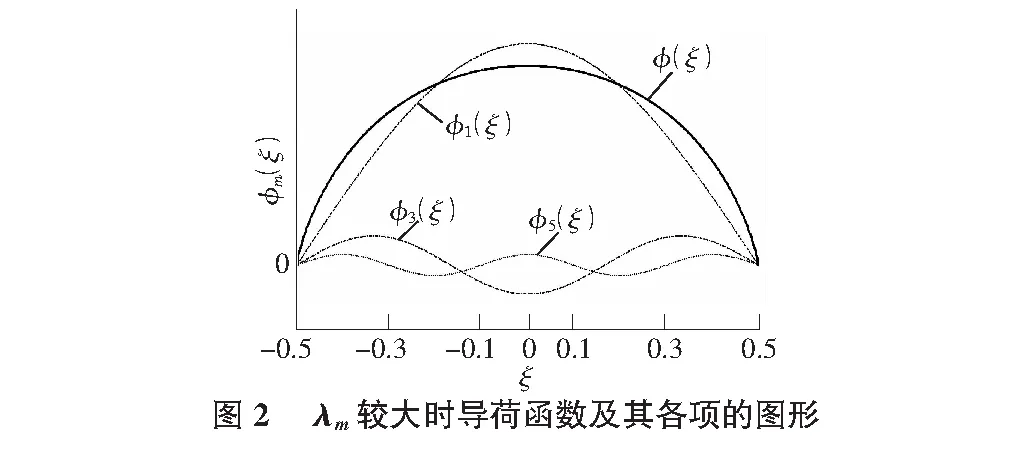
這也就說明了λm足夠大時,φ(ξ)的圖形是和φ1(ξ)比較接近的,亦比較接近三角形或者至少可以用三角形去近似計算。在傳統的梁板結構中,梁的彎曲剛度遠大于板,因而可以采用三角形分布的導荷方式將板上荷載傳遞給梁。
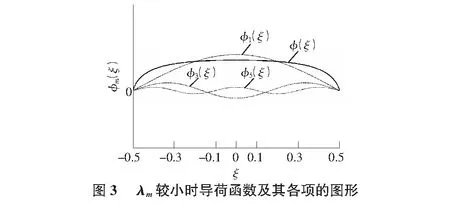
當λm較小時,根據式(13)導荷函數可近似為式(15),見圖3。
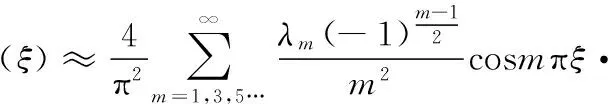
(15)
與前一種情況相對應地,隨m增大,級數各項的振幅近似以m-1速率衰減,衰減速率要慢得多,且φ(ξ)受級數高階項的影響不可忽略,其圖形也不再可以近似是三角形。這種情況就對應于厚板結構,梁的彎曲剛度與板比較接近,這時板向梁所導的荷載不能再以三角形分布來考慮。
當λm足夠大,且αm也足夠大時,導荷函數可近似為:
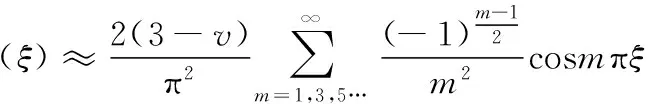
(16)
那么對于混凝土樓板(v=0.2),φ(ξ)形狀如圖4所示,最大值約為0.567。φ(ξ)的圖形近似于一個等腰直角三角形,這正對應于傳統的單向板導荷情況。

這樣,導荷函數以一個統一的表達式φ(ξ)描述了梁板結構在特定約束條件下的導荷方式;并且隨梁板剛度變化和板的尺寸變化,導荷函數的圖形可退化至傳統設計的簡化情況,驗證了推導的正確性。
3 算例
以一個給定參數的梁板結構為算例。簡圖同圖1,a和b均為8.4m,梁彎曲剛度C=2.722×109N/m2,板彎曲剛度D=1.4×109N/m2,材料的泊松比v=0.2,面荷載q=100kN/m2。
通過兩種方法計算得到板的變形如圖5所示,其中圖5a)為基于有限元方法的數值解(單位mm),圖5b)為基于板殼理論的解析解(單位m)。可以看出兩者在形狀和數值上是一致的。

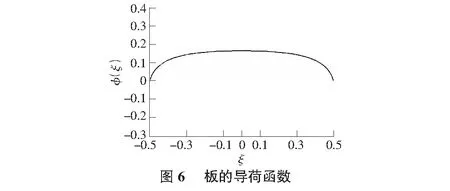
由式(13)計算得到板的導荷函數,如圖6所示。
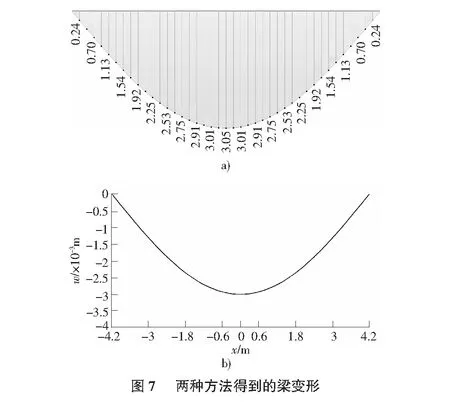
下面通過兩種方法計算梁的撓度如圖7所示,圖7a)為利用有限元方法計算整個梁板結構在面荷載作用下梁的撓度(單位mm),圖7b)為計算單獨的梁在圖6所示導算荷載下的撓度(單位m)。同樣地,可以看出兩者在形狀和數值上是一致的。
從而,上述計算驗證了板上的荷載確實是以式(13)所示的導荷函數的形式傳遞給了梁,導荷函數顯示了梁板結構傳遞荷載的方式。
4 結語
本文基于板殼理論,針對對邊簡支對邊彈性梁的矩形板進行分析。首先計算板撓度曲面的理論解,而后從梁的變形反推被導算到梁上的荷載,并以導荷函數的形式來描述。通過研究導荷函數的性質,揭示矩形板的平面尺寸和梁板間的剛度關系對結構導荷方式的影響。
[1] 曾昭陽.框架結構內力考慮樓板剛度變化影響的有限元分析[D].長沙:中南大學,2011.
[2] 程新春,顧祥林,孫 凱.梁板結構有限元分析的非等效荷載處理方法[J].結構工程師,2011,27(4):28-33.
[3] Timoshenko S,Woinowsky-Krieger S.Theory of Plates and Shells[D].Mcgraw-Hill College,1959.
[4] 結構計算軟件YJK-A用戶手冊及技術條件[Z].
The beam and slab structure load transfer way based on plate shell theory
Gao Yang
(Shanghai Municipal Engineering Design & Research Institute(Group) Limited Company, Shanghai 200092, China)
From the plate shell theory, this paper firstly calculated the theory resolution of plate deflection curved surface, then from the deformation of beam inversed guiding calculation beam load, and made discussion taking the form of load transfer function, through the nature of load transfer function research, clearly reflected the influence of plane size of rectangular plate and the stiffness relationship of beam and plate to structure load transfer form.
beam and slab structure, rectangular plate, load transfer way, load transfer function, plate shell theory
1009-6825(2017)12-0049-03
2017-02-14
高 揚(1984- ),男,博士,工程師
TU311
A

