擋土墻被動土壓力分布特性研究
梁 浩 然
(國防科學技術大學信息系統與管理學院,湖南 長沙 410073)
?
·巖土工程·地基基礎·
擋土墻被動土壓力分布特性研究
梁 浩 然
(國防科學技術大學信息系統與管理學院,湖南 長沙 410073)
比較了兩種均以經典庫侖土壓力為基礎的被動土壓力計算方法,通過算例分析發現,兩種方法在考慮墻后填土黏聚力和填土與墻背之間黏聚力的情況下,均能給出相同的破裂角,但是當計算被動土壓力大小和分布的時候,兩者在分布特性和數值大小上均有一定的差距,最后給出了產生這種結果的原因。
擋土墻,被動土壓力,破裂角,分布特性
擋土墻墻背作用土壓力大小的計算和分析是土力學中一個經典的課題。早在1773年和1857年庫侖和朗肯根據各自的假設給出了經典的庫侖土壓力理論計算公式和朗肯土壓力計算公式,它們是分別以土體整體極限平衡和土體為單元平衡為條件推導出來的。經典庫侖土壓力理論無法考慮土體自身的黏聚力,且因為其推導過程中取滑動土體進行整體受力分析通常獲得的是土壓力合力,難以求得土壓力的分布情況和土壓力合力作用點的位置。考慮到上述情況,以庫侖土壓力為基礎,給出了能考慮土體黏聚力和土體與墻背之間黏聚力等因素影響的計算公式,較大的拓展了庫侖土壓力理論的應用范圍。在這些計算公式的推導中,比較常見的是兩種,一種[1,2]仍然是采用整體分析,計算單元的底邊平行于破裂面,在滑動面上考慮了因為土體黏聚力產生的阻止土體運動的力,在本文稱此法為方法1;一種[3,4]是采用微分層單元法進行分析,微分層的劃分是平行于填土傾角的,在本文稱此法為方法2;本文試圖根據已有文獻中的研究成果,通過具體的算例比較這兩種計算方法給出結果的異同。
1 兩種方法的定性比較
方法1的整體思路仍然是整體分析方法,只是在受力分析時相比經典的庫侖土壓力理論多考慮了填土本身的黏聚力以及土體與墻背之間的黏聚力,然后利用兩個方向合力的平衡求解得到墻背對土體的反力和土體破裂面上對滑動土體的反力。
在文獻[1]采用此法求解破裂角θcr的計算中發現部分參數與高度h的取值有關,即認為土壓力沿著墻背應是非線性分布。但是如果依據此法的推導過程分析的話,如果相關幾何參數和力學參數確定的話,其實真實的θcr只有一個,θcr的大小并不會隨著高度h的變化而變化,所以方法1的推導過程可以判斷土壓力是沿著墻背線性分布的。
方法2在推導過程中采用的是平行于填土面傾角的β微分層單元,分析這一個微分層單元在極限狀態下的受力,通過兩個方向合力的平衡和繞土體微分層單元某點力矩的平衡建立方程,利用的荷載邊界條件,得到墻背土壓力的分布以及相關的計算公式。
在墻背被動土壓力的計算公式中存在下列奇異項:
p(h)=f{(H-h)-a}
(1)
其中,p為墻背上被動土壓力的大小;H為擋土墻豎直方向的高度;h為所需求的土壓力分布點高度,從中可以看到當h=H時p將變得無窮大,這與實際情況不符。
2 兩種方法的算例比較
下面通過算例來說明兩種被動土壓力計算方法的異同。
2.1 破裂角的計算
在被動土壓力情況下,墻體擠壓土體時,土壓力隨之增大,這時首先在土體中出現的滑動面,對應的土壓力必定是所有假設滑動面中對應的土壓力最小的一個,此時滑動面與水平面的夾角θcr稱為破裂角。
假設擋土墻相關參數如下:H=10 m,q=20 kPa,γ=18.5 kN/m3,β=5°,φ=30°,δ=15°,填土本身的黏聚力假設為cφ、墻背與填土間的黏聚力假設為cδ。比較在不同的cφ和cδ下兩種方法給出的破裂角。
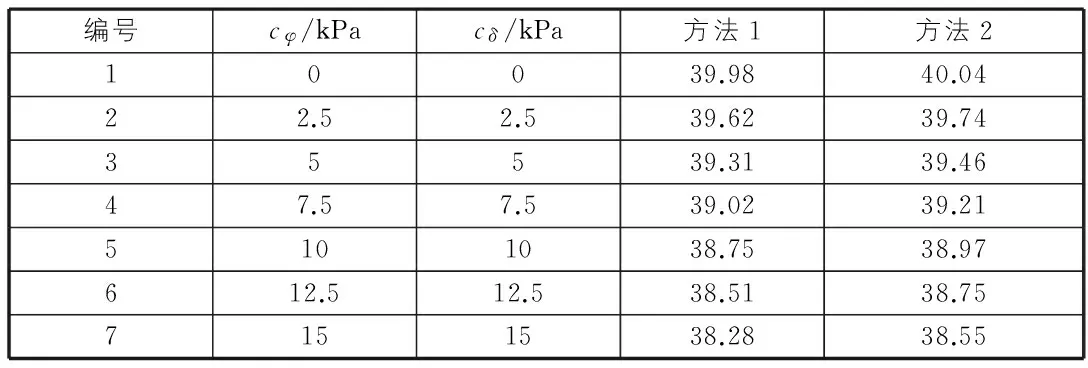
表1 黏聚力的變化對θcr的影響
表1為墻背傾角α=70°時的計算結果。從表1可以看出,隨著黏聚力cφ和cδ不斷變化,方法1和方法2幾乎給出了相同的破裂角。雖然黏聚力的變化明顯,但是破裂角的變化卻十分小,這說明黏聚力的變化對破裂角的影響較小。
表2是不同的墻背傾角對破裂角的影響。可以看到,相比黏聚力cφ和cδ,墻背傾角變化對破裂角的影響明顯增大,隨著墻背傾角的減小破裂角的數值逐漸增大,而且開始增長的比較快,墻背傾角減小到80°以后增長又趨于平緩。而且從中也進一步可以看出,黏聚力的變化對破裂角的影響十分有限,即使cφ和cδ的數值已經增加了1倍,但是破裂面的變化角度不超過1°。
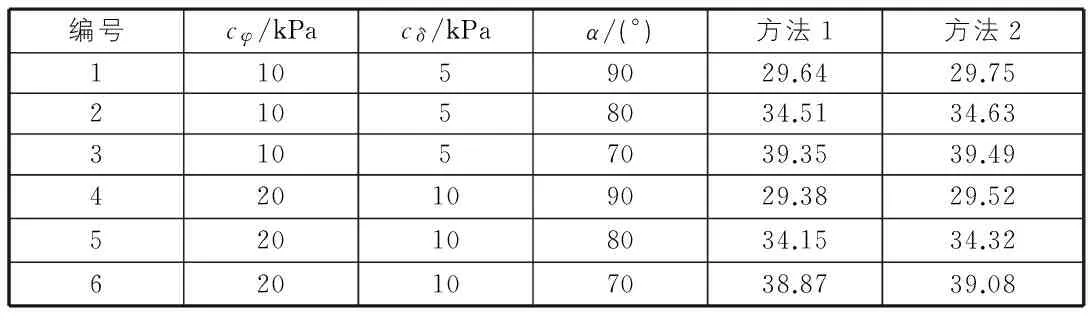
表2 墻背傾角α的變化對θcr的影響
2.2 墻背被動土壓力分布的計算
計算參數如下:H=8 m,q=10 kPa,γ=17.5 kN/m3,α=90°,β=5°,φ=30°,δ=15°,cδ=0。
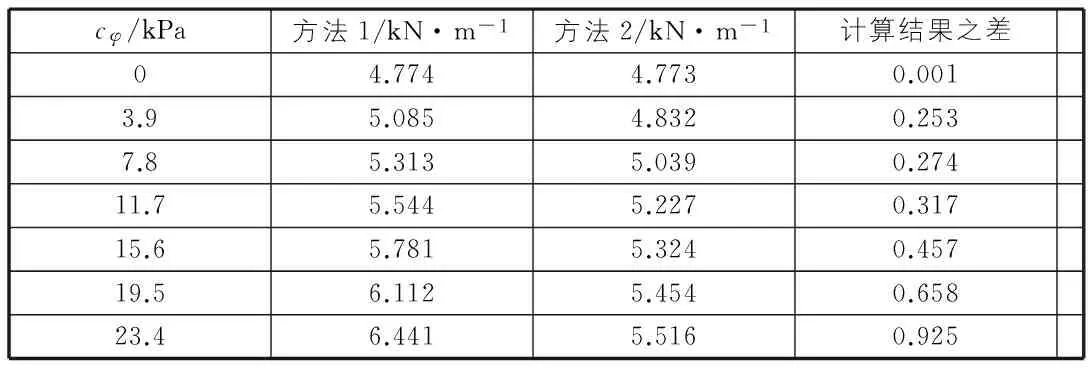
表3 被動土壓力的計算結果
表3比較了在不同cφ下被動土壓力的計算結果。從中可以看出,當cφ=0時,兩者給出了一樣的結果。當cφ≠0時,兩種方法給出的結果差別較大,而且隨著cφ的增大這種差別也在不斷增大,說明兩者給出了不一樣的計算結果。
產生這種差別的主要原因是兩種方法在推導的過程中選取微單元的方法不同,方法1在推導過程中選取的是沿著與破裂面平行的計算單元,而方法2在推導過程中選取的沿著與上覆蓋土體平行的微單元。從上面的關于兩種方法的比較算例也可以看出被動土壓力的計算還需要更進一步深入研究。
3 結語
本文通過定性分析和定量計算,比較了兩種不同的土壓力計算方法,指出兩種方法在破裂角的計算中均能給出一致的結果,但是在被動土壓力大小的計算中給出的結果卻有較大的差別,這種差別隨著土體黏聚力的增加逐步加大,出現這種現象的主要原因在于兩種方法推導中選取的計算微單元不同。
[1] 彭明祥.擋土墻被動土壓力的庫侖統一解[J].巖土工程學報,2008,30(12):1783-1788.
[2] 馬崇武.黏性擋土墻被動土壓力的計算[J].蘭州理工大學學報,2016,42(1):124-127.
[3] 林宇亮,楊果林,黃向京.擋墻后粘性土被動土壓力的薄層單元法[J].公路交通科技,2011,28(3):13-19.
[4] 楊 敏,劉 斌,周建武.擋土墻主動和被動土壓力的統一解[J].同濟大學學報(自然科學版),2011,39(2):187-193.
The distribution characteristic of passive earth pressure on retaining walls
Liang Haoran
(College of Information System and Management, National University of Defense Technology, Changsha 410073, China)
Two methods which have been given in the existed literature to compute the passive earth pressure are compared. The numerical results show that when the cohesion of filler and conhesion between filler and wall back are considered, two methods give the same results of critical rupture angle. As to the distribution characteristic and magnitude of passive earth pressure, the results given by the two methods are different. Finally gives the reason which cause the difference.
retaining walls, passive earth pressure, critical rupture angle, distribution characteristic
1009-6825(2017)12-0051-02
2017-02-11
梁浩然(1979- ),男,工程師
TU476.4
A

