基于模態(tài)參數(shù)識別的懸架系統(tǒng)狀態(tài)監(jiān)測方法及試驗(yàn)研究
李苗碩,谷豐收,王鐵,李國興,,王永紅,鹿星晨
(1.太原理工大學(xué)機(jī)械工程學(xué)院車輛工程系,山西 太原 030024;2.哈德斯菲爾德大學(xué)工程與效能中心,曼徹斯特 HD1 3DH;3.大運(yùn)汽車股份有限公司,山西 運(yùn)城 044000)
基于模態(tài)參數(shù)識別的懸架系統(tǒng)狀態(tài)監(jiān)測方法及試驗(yàn)研究
李苗碩1,谷豐收2,王鐵1,李國興1,2,王永紅3,鹿星晨1
(1.太原理工大學(xué)機(jī)械工程學(xué)院車輛工程系,山西 太原 030024;2.哈德斯菲爾德大學(xué)工程與效能中心,曼徹斯特 HD1 3DH;3.大運(yùn)汽車股份有限公司,山西 運(yùn)城 044000)
懸架系統(tǒng)直接關(guān)系到車輛的安全性、平順性和操穩(wěn)性,由于路面激勵是隨機(jī)激勵,對懸架系統(tǒng)的狀態(tài)監(jiān)測一直是研究難點(diǎn)。該文提出一種新的懸架狀態(tài)監(jiān)測方法,利用僅需輸出的平均相關(guān)隨機(jī)子空間法識別模態(tài)參數(shù),再通過模態(tài)參數(shù)變化對故障造成的懸架剛度變化進(jìn)行監(jiān)測。首先對平均相關(guān)隨機(jī)子空間法在較高阻尼比下的識別效果進(jìn)行分析,驗(yàn)證算法在懸架監(jiān)測中的可行性;然后基于車輛七自由度振動模型對模態(tài)參數(shù)進(jìn)行仿真識別,分析路面激勵及噪聲對識別結(jié)果的影響,并提出基于振型和模態(tài)能量的監(jiān)測方法;最后設(shè)計利用9軸MEMS慣性傳感器的試驗(yàn)方案對正常及故障狀態(tài)進(jìn)行監(jiān)測,驗(yàn)證方法的可信度。
模態(tài)參數(shù)識別;懸架系統(tǒng);平均相關(guān)隨機(jī)子空間法;狀態(tài)監(jiān)測;MEMS
0 引言
有關(guān)車輛懸架系統(tǒng)的大量研究結(jié)果表明,車輛懸架系統(tǒng)直接關(guān)系到車輛通過性、運(yùn)行穩(wěn)定性、平順性、安全性以及操縱穩(wěn)定性[1-4]。為了確保懸架裝置正常運(yùn)行,對懸架系統(tǒng)進(jìn)行狀態(tài)監(jiān)測成為近期研究的熱點(diǎn)[5-6]。有些研究采用數(shù)據(jù)驅(qū)動方法,即基于對某振動信號的直接測量進(jìn)行時域和頻域分析來實(shí)現(xiàn)故障檢測[7-9]。但懸架系統(tǒng)的振動與行車速度和路面激勵的耦合關(guān)系較為復(fù)雜,為特征不明顯的非平穩(wěn)隨機(jī)信號,較難有效提取故障信息。近年來,很多研究將基于模型的監(jiān)測方法作為重點(diǎn),并取得了一定的成功[10-11]。
隨機(jī)子空間法(SSI)作為隨機(jī)激勵下僅需輸出的識別方法,識別準(zhǔn)確且所需設(shè)備簡便,得到了很多研究者的重視。Yuan[12]用隨機(jī)子空間法估計車輛的操控動力模型參數(shù);Dong等[13]用隨機(jī)子空間法識別車輛模態(tài)并計算車輛慣性參數(shù)變化,并提出較高的阻尼比(20%~30%)對隨機(jī)子空間法的識別結(jié)果有較大的影響。Chen等[14]提出了基于平均相關(guān)函數(shù)的隨機(jī)子空間算法(ASC-SSI),有效抑制噪聲干擾且需處理的數(shù)據(jù)量小,適合結(jié)構(gòu)在線狀態(tài)監(jiān)測。綜合上述,本文提出一種監(jiān)測方法,通過識別模態(tài)參數(shù)變化判斷懸架彈簧剛度變化,對懸架系統(tǒng)進(jìn)行在線狀態(tài)監(jiān)測。
1 數(shù)值模擬驗(yàn)證
1.1 平均相關(guān)隨機(jī)子空間法基本原理
隨機(jī)子空間算法(SSI)作為一種僅需響應(yīng)數(shù)據(jù)的識別算法,不需要獲取激勵數(shù)據(jù)且適用于隨機(jī)激勵下的模態(tài)識別。利用對響應(yīng)數(shù)據(jù)的協(xié)方差構(gòu)成的矩陣進(jìn)行奇異值分解,獲得可控制矩陣和可觀測矩陣,基于可觀測矩陣的推移不變性計算狀態(tài)矩陣,最終識別出模態(tài)參數(shù)。平均相關(guān)隨機(jī)子空間法(ACS-SSI)采用多次平均后的相關(guān)函數(shù)信號取代原算法采用的響應(yīng)信號作為算法輸入,從而使其復(fù)雜工況下有更好的識別精度。在隨機(jī)激勵的模態(tài)識別中激振力一般是隨機(jī)的,且與噪聲很難區(qū)分,系統(tǒng)模型常被寫成隨機(jī)型離散狀態(tài)空間方程:
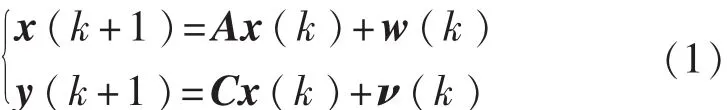
式中:A——離散狀態(tài)矩陣;
C——輸出矩陣;
w(k)——隨機(jī)輸入并包含處理過程噪聲;
ν(k)——測量噪聲;
k——某離散時刻值。
狀態(tài)矩陣A中包含系統(tǒng)信息,隨機(jī)子空間法通過響應(yīng)將狀態(tài)矩陣A還原,并將其中的模態(tài)參數(shù)提取出來。假設(shè)由l個通道共同采集的l路測量信號組成的矩陣為y(t),在其中選擇信噪比較好的一路信號,設(shè)為第k路信號的yk(t),可得所有原信號關(guān)于第k個通道的相關(guān)函數(shù)為
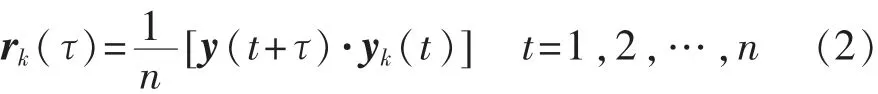
N為采集數(shù)據(jù)的總長度,τ=1,2,…,N-n,為相關(guān)函數(shù)的離散時間序列。相關(guān)函數(shù)rk(τ)∈Rl·τ為一個l路關(guān)于τ的一組相關(guān)函數(shù)信號。為使消噪效果更明顯進(jìn)行多組試驗(yàn)得到了多組信號rk1,rk2,…,rkn,對其取平均后得到平均相關(guān)函數(shù),用代替原y(t)作為輸入進(jìn)行模態(tài)識別。
之后方法與協(xié)方差驅(qū)動的隨機(jī)子空間方法相同[15]:用由的協(xié)方差構(gòu)成矩陣T1|i,并對其進(jìn)行奇異值分解(SVD),從而得到離散狀態(tài)矩陣A,A特征值分解后得到特征值λi及特征向量Ψi,將其最終轉(zhuǎn)化為固有頻率fni、模態(tài)阻尼比ξi以及模態(tài)向量νi。
1.2 識別驗(yàn)證
由于高阻尼比對識別結(jié)果的影響,隨機(jī)子空間法在阻尼比達(dá)到20%~30%的情況還較少被應(yīng)用[13]。但是車輛懸架系統(tǒng)阻尼比較高,阻尼比最高的一階一般超過20%~30%。為了驗(yàn)證改進(jìn)后的平均相關(guān)子空間算法在高阻尼比下的可靠性,建立三自由度數(shù)值模擬系統(tǒng)如圖1所示。系統(tǒng)中3個質(zhì)量塊m1、m2、m3由3個固定剛度k1、k2、k3的彈簧和阻尼器c1、c2、c3連接。因固有頻率由質(zhì)量和剛度共同決定,系統(tǒng)的固有頻率不變,為fn1=2.5Hz,fn2=5.8Hz,fn3=9.9Hz。然后將不相關(guān)的3個低通濾波后的白噪聲信號w1,w2,w3分別施加在3個質(zhì)量塊上模擬隨機(jī)激勵。設(shè)置不同的阻尼比如表1所示,共9次試驗(yàn)使阻尼比在2.5%~40%變化,觀察對比隨機(jī)子空間法(SSI)和平均相關(guān)隨機(jī)子空間法(ACS-SSI)隨阻尼比變化識別誤差的變化情況。
設(shè)置采樣頻率為200Hz,采用奇異值突變結(jié)合穩(wěn)態(tài)圖定階方法,并設(shè)置模態(tài)置信度(MAC)為30%,避免虛假模態(tài)被識別。設(shè)置仿真數(shù)據(jù)時長100 s,ACS-SSI進(jìn)行50次平均。每個阻尼比進(jìn)行10次蒙特卡洛試驗(yàn),識別誤差的均值由圖2所示。
由于阻尼比對振動周期性的衰減隨著阻尼的增大,識別結(jié)果的誤差隨之增大,但ACS-SSI始終優(yōu)于SSI,尤其在阻尼比>25%之后。對比在最高阻尼比(40%)下,ACS-SSI(3.9%)頻率誤差保持在SSI(8.7%)的一半以下;阻尼比誤差A(yù)CS-SSI(29.3%)雖然低于SSI(42.4%),但是兩者誤差都過大而且很不穩(wěn)定;對比模態(tài)向量誤差,ACS-SSI(2.1%)和SSI(6.3%)的趨勢基本與頻率誤差相一致并且穩(wěn)定。由此可看出,ACS-SSI的識別結(jié)果明顯優(yōu)于SSI,尤其是頻率和模態(tài)向量誤差很小;阻尼比的識別雖有一些提升,但誤差依然較大且不穩(wěn)定。
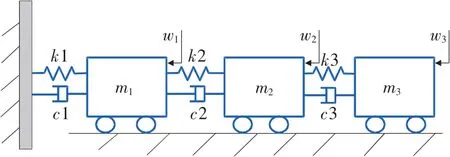
圖1 三質(zhì)量振動模型

表1 算例阻尼比參數(shù)
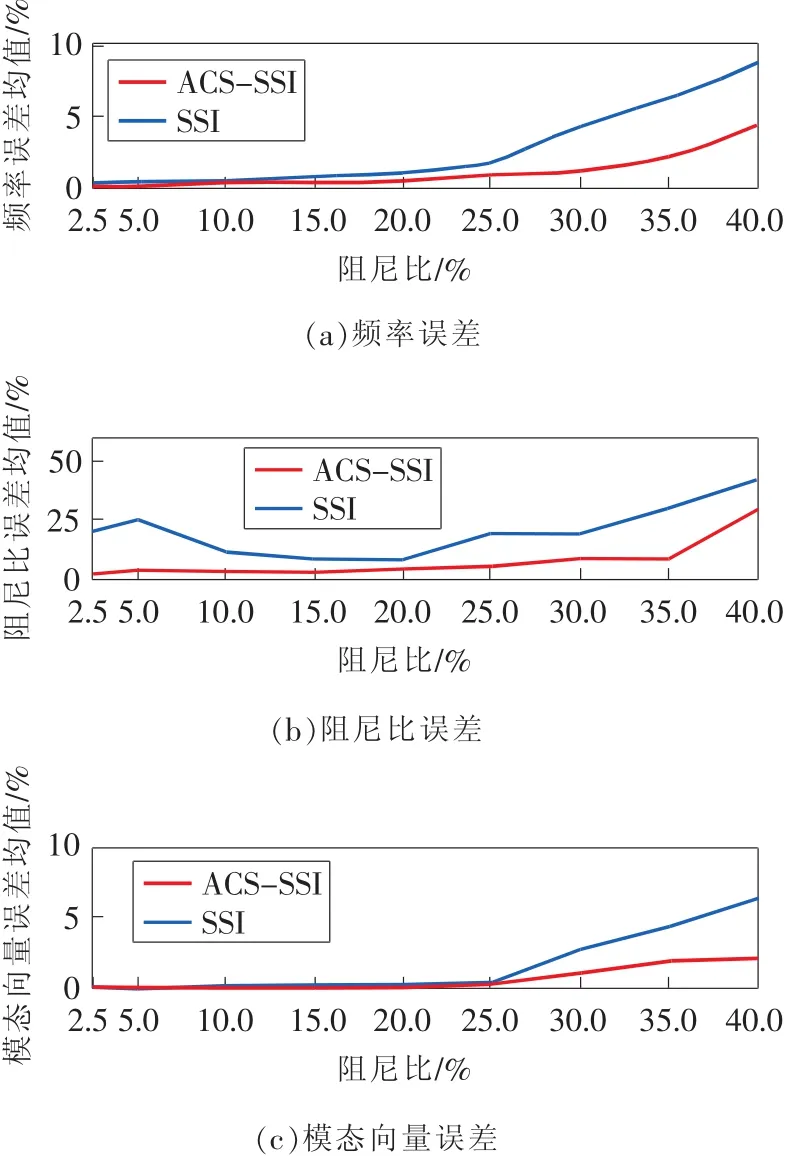
圖2 比較ACS-SSI和SSI的頻率誤差、阻尼比誤差和模態(tài)向量誤差均值
這是由于ACS-SSI使用多次平均后的相關(guān)函數(shù)(圖3(a))作為輸入,相比原始加速度信號(圖3(b)周期性更強(qiáng)),通過平均相關(guān)計算降低了原加速度響應(yīng)信號中的隨機(jī)成分。因此從二者的識別穩(wěn)態(tài)圖(圖4)也可以看出,ACS-SSI的穩(wěn)定性更強(qiáng),識別結(jié)果更加收斂。
由此可以判斷,在較高阻尼比的情況下,平均相關(guān)隨機(jī)子空間法依舊適用且保持了相當(dāng)?shù)木取DB(tài)頻率和模態(tài)向量誤差都較小,但是由于模態(tài)向量受車速和載荷影響較小,因此選擇基于模態(tài)向量的方法進(jìn)行狀態(tài)監(jiān)測。
2 模態(tài)仿真分析及識別
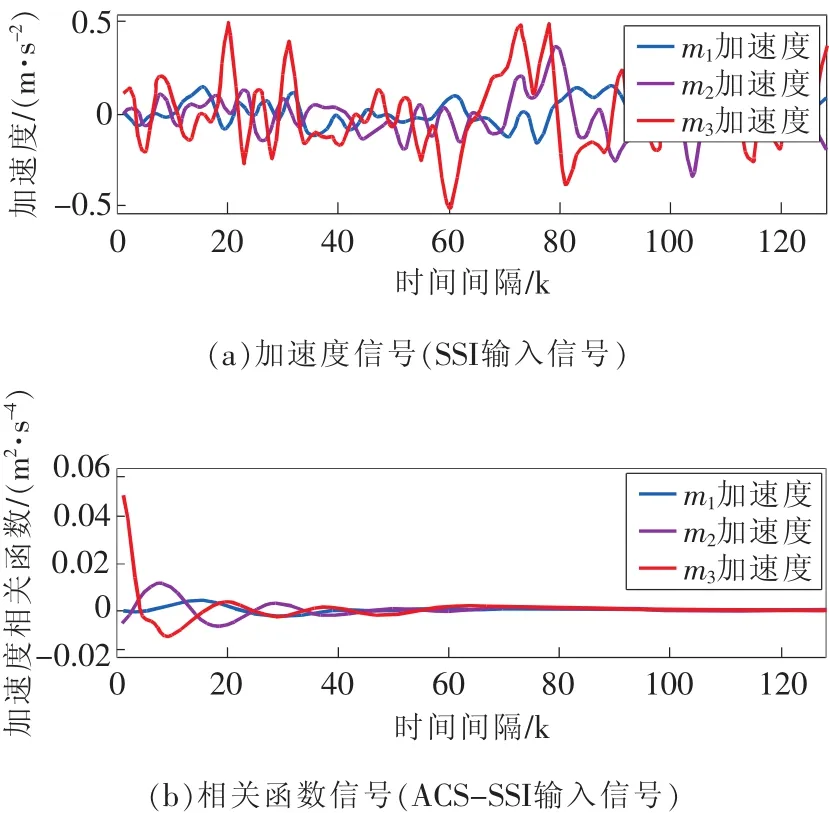
圖3 SSI的輸入信號和ACS-SSI的輸入信號
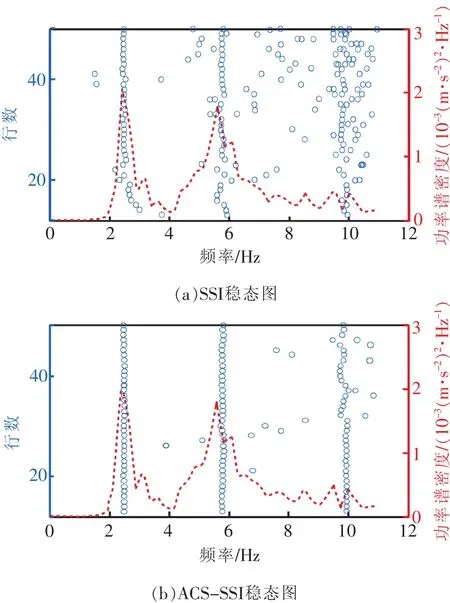
圖4 SSI和ACS-SSI穩(wěn)態(tài)圖
為了進(jìn)一步研究基于ACS-SSI的懸架狀態(tài)監(jiān)控系統(tǒng),建立七自由度的振動模型,用Simulink生成的四輪路面不平度時域信號輸入到正常和故障模型中進(jìn)行激勵,最后利用得到的仿真響應(yīng)信號進(jìn)行模態(tài)識別,從而對彈簧故障進(jìn)行仿真識別。圖5為仿真分析過程示意圖。
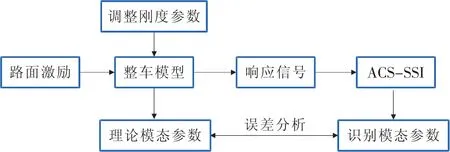
圖5 仿真分析示意圖
2.1 七自由度車輛振動模型
針對某車型乘用車建立七自由度整車振動模型(圖6),由于運(yùn)行時整車載荷不變將車身質(zhì)量簡化為m0和簧下質(zhì)量(m1,m2,m3,m4)、懸架彈簧及減震器組成質(zhì)彈阻模型。因仿真中車輛始終在較平坦的B級路面上直線行駛,將懸架彈簧剛度和減震器阻尼值分別線性化用k1,k2,k3,k4和c1,c2,c3,c4表示,輪胎剛度用kt1,kt2,kt3,kt4表示。

圖6 七自由度車輛振動模型
根據(jù)某車型參數(shù)建立動力學(xué)平衡方程組,并整理為矩陣形式:
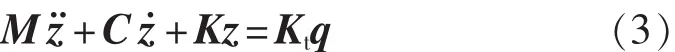
式中M、C、K分別是根據(jù)動力學(xué)微分方程整理得的質(zhì)量陣、阻尼陣以及剛度陣。狀態(tài)向量z=[z,θ,φ,z1,z2,z3,z4]T分別代表車身垂向位移、俯仰角、側(cè)傾角及4個簧下質(zhì)量位移,向量q=[q1,q2,q3,q4]T為路面輸入的4個位移向量。

為方便仿真和識別,轉(zhuǎn)化為狀態(tài)空間模型。將式(3)通過式(4)變換為狀態(tài)空間方程式:

2.2 模態(tài)分析
將狀態(tài)矩陣A特征分解后可得到模態(tài)固有頻率fn、阻尼比ξ以及模態(tài)向量ν。第i階模態(tài)向量ν(i)為固有頻率fni對應(yīng)的特征向量,代表此模態(tài)頻率下狀態(tài)向量z=[z,θ,φ,z1,z2,z3,z4]T中各變量的振幅比。由表2看出,由于懸架是一個欠阻尼窄帶低通系統(tǒng),模態(tài)頻率主要集中于低頻,而所有阻尼比都超過了20%,俯仰和側(cè)傾兩階阻尼比高達(dá)34%和38%。
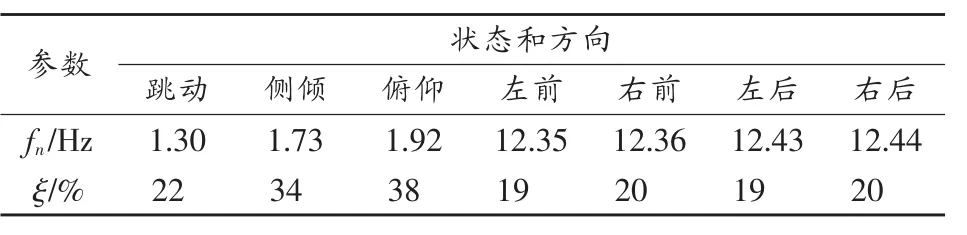
表2 車輛模態(tài)頻率及阻尼比
模態(tài)向量中的前3項(xiàng)(ν1,ν2,ν3)代表跳動、側(cè)傾和俯仰(z,θ,φ)的振幅比,反映車身振動形態(tài)。為能直觀表達(dá),用式(6)將(ν1,ν2,ν3)投影到車身4個角,根據(jù)它們的振幅比(νa,νb,νc,νd)得到前三階車身振型圖(見圖7)。代表車身跳動、側(cè)傾和俯仰模態(tài)的振動形態(tài),需要特別指出的是在理想的跳動和俯仰模態(tài)中不包含側(cè)傾的運(yùn)動,其左右兩側(cè)模態(tài)向量總是一致的。這也說明振型變化,尤其兩側(cè)振型的差異增大可以反映出車輛的故障情況。
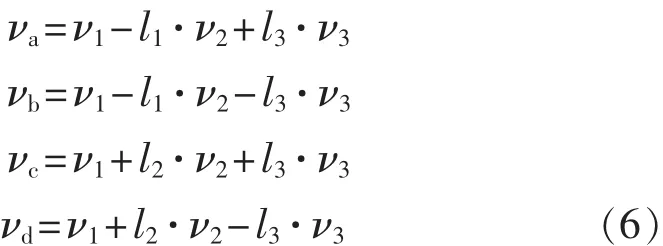
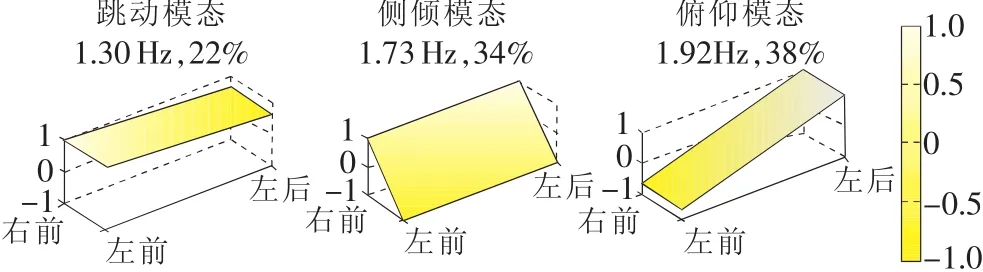
圖7 車身模態(tài)振型
2.3 剛度變化對模態(tài)參數(shù)的影響
車輛在長期的運(yùn)行過程中載荷狀況、環(huán)境因素以及溫度影響會造成懸架空簧失氣、鋼簧裂紋、鋼簧斷裂等故障,引起懸架的性能參數(shù)發(fā)生變化,如彈簧剛度的下降。為模擬故障以左后懸架為例,改變0%~50%左后懸架彈簧的剛度以模擬懸架參數(shù)變化,分析其對模態(tài)參數(shù)的影響。圖8表示跳動模態(tài)和俯仰模態(tài)的固有頻率fn1、fn3以及模態(tài)向量中的側(cè)傾分量ν3(1)、ν3(3),其代表側(cè)傾運(yùn)動的占比。可以看出,兩階模態(tài)的頻率隨剛度降低而下降、側(cè)傾模態(tài)向量的模隨剛度下降從零開始增大,說明懸架發(fā)生故障會增加車身的側(cè)傾振動。
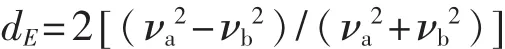
為了通過車身振型(νa,νb,νc,νd)表示側(cè)傾振動成分的大小,通過式(7)計算左右振型大小的差異,dE為模態(tài)能量差異。由圖9可以看出,跳動和俯仰兩階的模態(tài)能量差異隨著某一懸架剛度下降都從零開始呈現(xiàn)明顯上升趨勢,因此模態(tài)能量差異可以作為懸架彈簧剛度變化進(jìn)行診斷和監(jiān)測的指標(biāo)。
2.4 路面仿真激勵及響應(yīng)
為得到更接近真實(shí)的車輛振動信號,利用Simulink仿真生成四輪輸入路面不平度時域信號。根據(jù)GB/T 7031——2005/ISO8608:11995《機(jī)械振動道路路面譜測量數(shù)據(jù)報告》的描述,將路面空間功率譜Gd(n)用以下擬合公式表示:
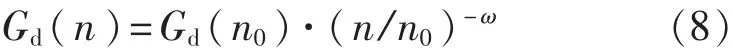
其中n為空間頻率,m-1。根據(jù)國標(biāo)n0=0.1m-1,為空間參考坐標(biāo);ω=2,為擬合功率譜密度指數(shù)。根據(jù)濾波白噪聲法,可將空間頻域式(8)轉(zhuǎn)化為路面不平度的傳遞函數(shù),將白噪聲輸入至傳遞函數(shù)組成的模塊中,即可得到四輪位移時域信號,圖10為Simulink仿真線框圖。
車輛直線行駛時,同側(cè)前后輪壓過相同輪轍,所以其信號幅值相同但是后輪相位滯后Δt=l/u,l為前后軸軸距、u為車速。而左右輪轍功率譜密度曲線不同,它們之間的相干函數(shù)為
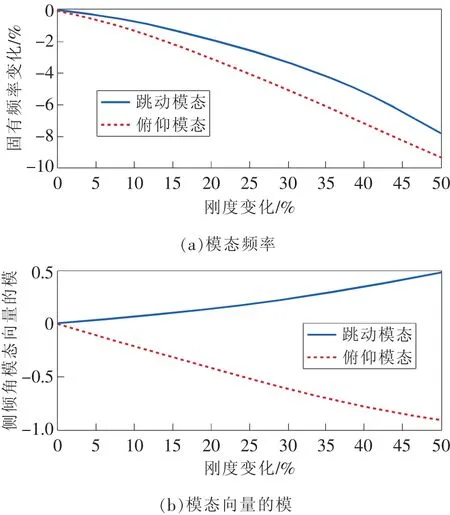
圖8 模態(tài)頻率及模態(tài)向量的模隨剛度變化
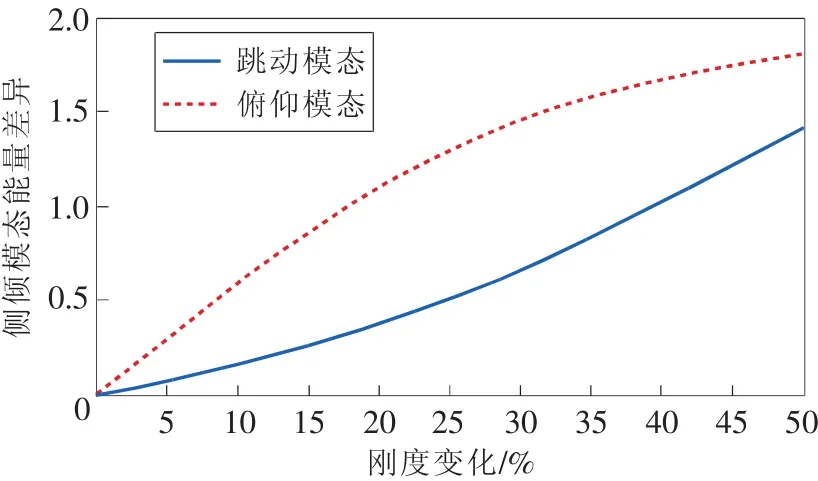
圖9 模態(tài)能量差異隨剛度變化
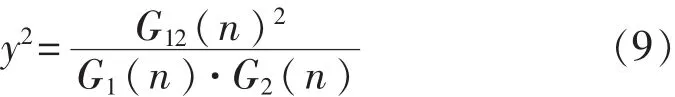
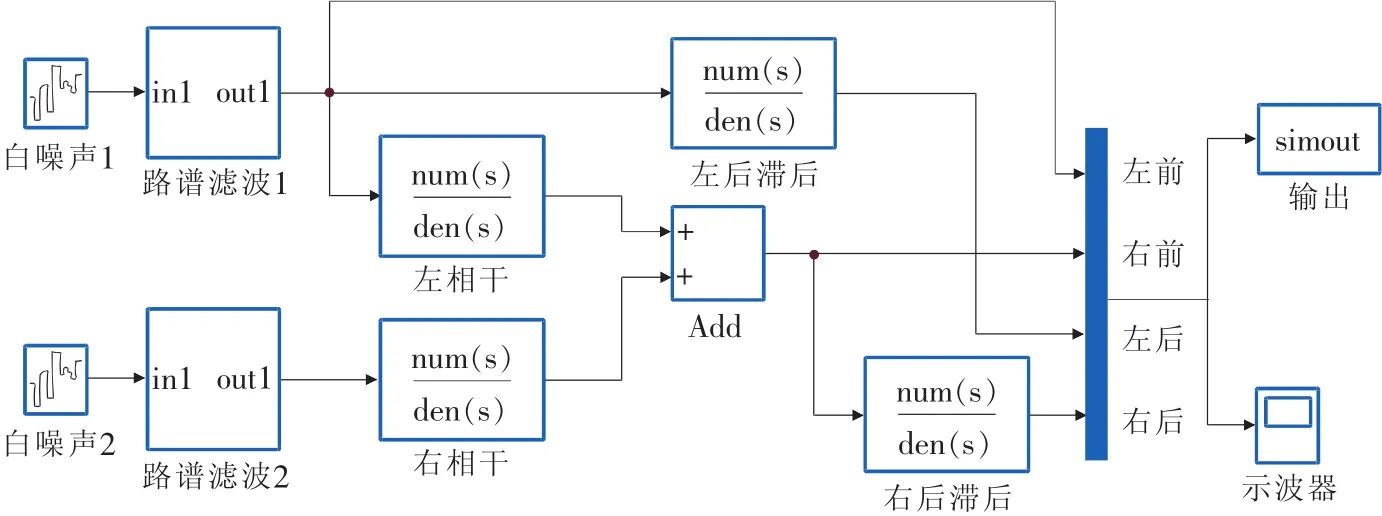
圖10 路面仿真Simulink線框圖
式(9)表示左右輪轍關(guān)系曲線。其低頻段相關(guān)性高,高頻段相關(guān)性低,使車輛收到的低頻段左右兩側(cè)激勵非常相似。這導(dǎo)致側(cè)傾模態(tài)不能被激勵出,所以2.3節(jié)未對側(cè)傾模態(tài)進(jìn)行討論。為了模擬實(shí)車試驗(yàn)中的路面,設(shè)置模型中輸入路面的粗糙度等級為B級。將路面不平度位移信號輸入車輛振動模型后可得到車身振動信號,將車身垂向加速度、俯仰角加速度和側(cè)傾角加速度3路信號進(jìn)行變換后作為模態(tài)參數(shù)識別的輸入變量。
2.5 仿真識別結(jié)果及誤差分析
在選取的仿真響應(yīng)信號中添加信噪比SNR=2的噪聲信號,模擬帶有測量噪聲的真實(shí)測量信號。再進(jìn)行平均相關(guān)子空間算法的模態(tài)識別,設(shè)置平均次數(shù)100次,每段數(shù)據(jù)時長為20 s,分別對左后懸架剛度為100%、90%、80%的3種狀態(tài)進(jìn)行識別和對比。
由于文中上述的側(cè)傾激勵有限等原因,仿真識別僅能識別出跳動和俯仰兩階模態(tài),其誤差均與數(shù)值模擬的結(jié)果相吻合,而且側(cè)傾趨勢也能被清晰的顯示出來。為了觀察是否能在現(xiàn)有誤差基礎(chǔ)上判斷出故障,對3種狀態(tài)分別進(jìn)行50次蒙特卡洛重復(fù)實(shí)驗(yàn),得到了3種狀態(tài)下模態(tài)能量差異的分布圖(見圖11)。可以看出,由于誤差影響,每次試驗(yàn)數(shù)值存在一定的波動,但10%的剛度變化造成的差異依然可以清晰地判斷出來,說明將模態(tài)能量差異作為狀態(tài)監(jiān)測的判斷故障依據(jù)是合理的。
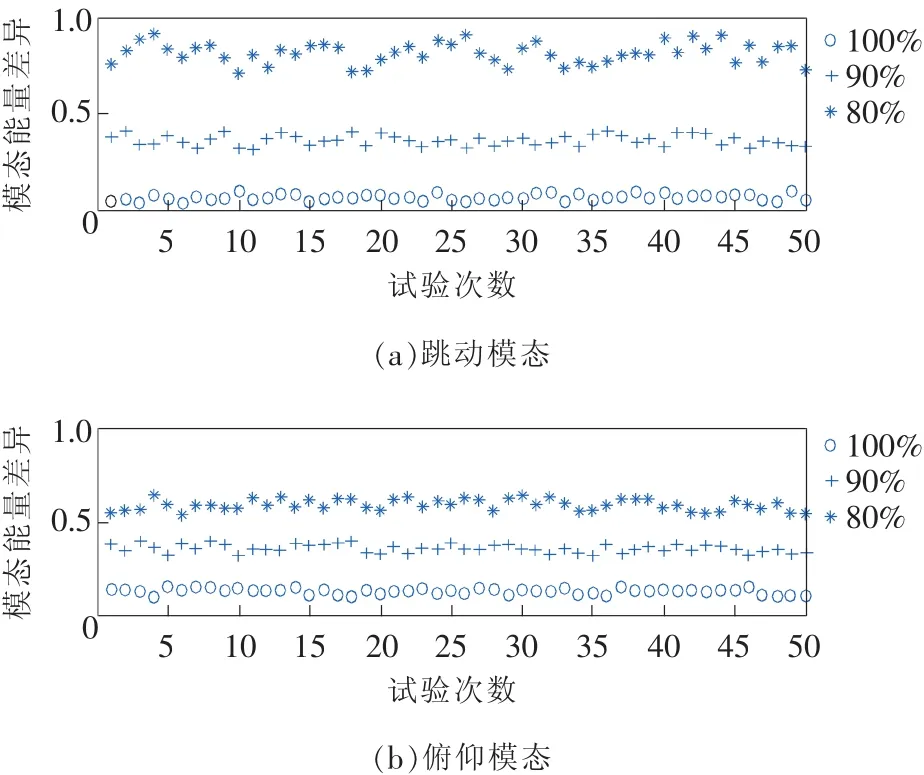
圖11 不同狀態(tài)下模態(tài)能量差異
3 實(shí)車試驗(yàn)
為了驗(yàn)證以上模態(tài)識別結(jié)果以及基于振型及模態(tài)能量監(jiān)測方法的可信度進(jìn)行路上實(shí)車試驗(yàn)。
3.1 試驗(yàn)方案
選用某小型乘用車為試驗(yàn)用車,利用MEMS慣性傳感器采集車身垂向加速度、俯仰角加速度和側(cè)傾角加速度數(shù)據(jù)。對兩種車況進(jìn)行路上試驗(yàn):1)原裝懸架作為基線;2)將左后懸架彈簧更換為原彈簧80%剛度的彈簧以模擬懸架故障。
在正常路況下行駛,車速保持在30 km/h左右,每種車況運(yùn)行60 km/h以上,并利用GPS統(tǒng)計里程和車速。路況由平整路況、少量減速帶和小段不平整路段組成。將車身振動的功率譜密度與不同路面等級仿真車身功率譜密度比較獲知,試驗(yàn)路面接近于B級標(biāo)準(zhǔn)路面。
3.2 傳感器布置
針對車身的3個變量,選擇MEMS慣性傳感器測量。隨著MEMS傳感器技術(shù)發(fā)展,其不僅可以同時采集加速度和角速度信號而且還具有頻率范圍大、精度高和成本較低等優(yōu)點(diǎn)。研究中選用的MPU-6050芯片量程達(dá)±16g,非線性<0.5%。
將傳感器布置在車底盤計算得到質(zhì)心位置(見圖12)。為減少噪聲干擾和位置誤差,經(jīng)多個方案對比后選擇將傳感器用陶瓷膠粘在10mm厚的鋼板上,再用螺栓將鋼板固定在車底盤的車架上。為減小安裝時的平行度誤差增加軸間耦合,安裝時需要保證傳感器坐標(biāo)系與車身坐標(biāo)盡可能地保持平行,并對安裝后的傳感器進(jìn)行側(cè)傾和俯仰測試,確認(rèn)X/Y的軸間耦合誤差<2%。

圖12 傳感器安裝和布置
3.3 試驗(yàn)數(shù)據(jù)處理與結(jié)果分析
對試驗(yàn)數(shù)據(jù)進(jìn)行預(yù)處理:首先為了排除非平穩(wěn)車速對響應(yīng)數(shù)據(jù)的干擾,剔除信號中縱向和橫向加速度過大的信號段,以減小非勻速和非直線運(yùn)動對識別結(jié)果的影響。再對信號進(jìn)行截止頻率為8Hz的低通濾波,去除發(fā)動機(jī)振動造成的影響(發(fā)動機(jī)工作轉(zhuǎn)數(shù)為800~2000 r/min)。完成以上等處理后將信號分為100段,每段20 s,其他參數(shù)設(shè)置與仿真識別基本相同。其識別的固有頻率及振型結(jié)果如圖13所示。
圖13(a)和圖13(b)為基線狀態(tài)下跳動和俯仰模態(tài)振型圖,圖13(c)和圖13(d)為一彈簧為原彈簧80%剛度下跳動和俯仰模態(tài)振型圖,從圖中可以看出二者的基本振動形態(tài)相同,但從陣型計算結(jié)果來看故障狀態(tài)的俯仰和側(cè)傾姿態(tài)大于正常狀態(tài)。
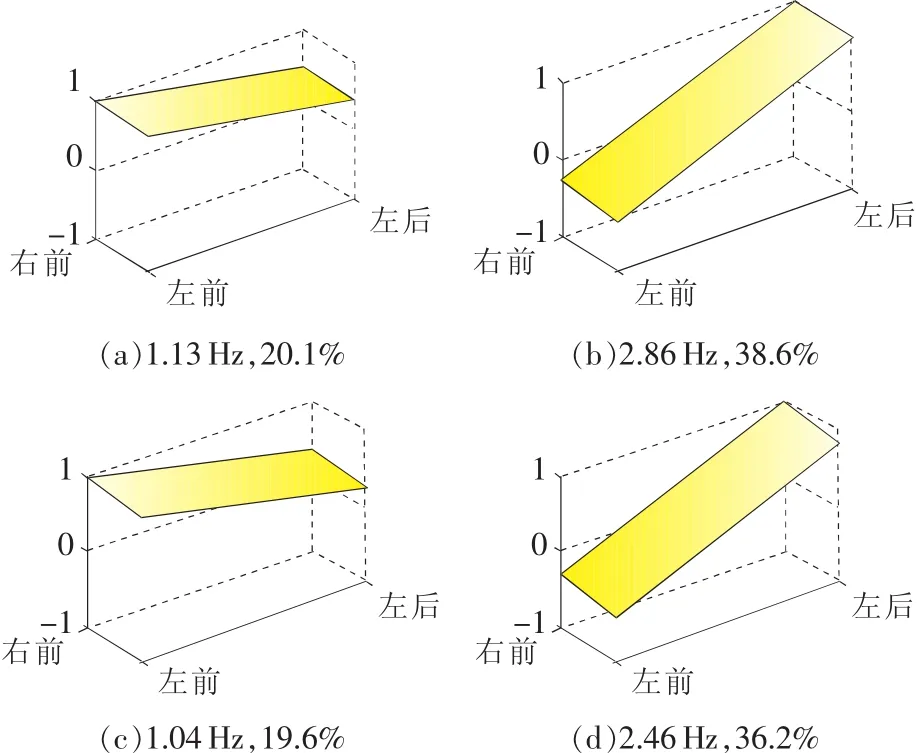
圖13 基線狀態(tài)與故障狀態(tài)模態(tài)參數(shù)
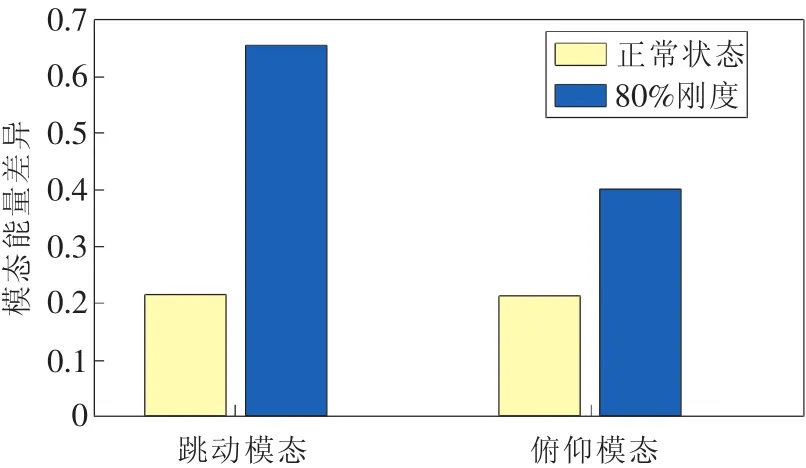
圖14 正常與80%剛度的模態(tài)能量差異
為了更清晰地表達(dá)振型變化,求其模態(tài)能量差異,從圖14可以看出,故障狀態(tài)下模態(tài)能量差異明顯大于基線狀態(tài)。由此實(shí)驗(yàn)結(jié)果可得,基于模態(tài)識別的方法,通過振型及模態(tài)能量差異的變化可以對懸架狀態(tài)進(jìn)行在線監(jiān)測。實(shí)際應(yīng)用時可對不同的車輛和故障形式進(jìn)行試驗(yàn)標(biāo)定,以得到理想的監(jiān)測效果。
4 結(jié)束語
本文通過研究平均相關(guān)隨機(jī)子空間算法在較高阻尼比情況下的識別準(zhǔn)確性,驗(yàn)證了該算法在懸架系統(tǒng)狀態(tài)監(jiān)測中的可行性。建立了一種利用識別模態(tài)參數(shù)變化的監(jiān)測方案,并用實(shí)車實(shí)驗(yàn)驗(yàn)證了該方案的可信性。本文方法為懸架系統(tǒng)的在線狀態(tài)監(jiān)測和故障診斷提供了一種具有較高準(zhǔn)確性與魯棒性的方法。
[1]徐道臨,張林,周加喜.重型礦用自卸車油氣懸架參數(shù)優(yōu)化[J].振動與沖擊,2012,31(24):98-101.
[2]王鐵,高昱,申晉憲.水罐消防車操縱穩(wěn)定性與平順性的仿真優(yōu)化[J].汽車工程,2012,34(12):1114-1118.
[3]SCHUMANN A R,ANDERSON R J.Optimal control of an active anti roll suspension for an off-road utility vehicle using interconnected hydragas suspension units[J]. Vehicle System Dynamics,2003,37(1):145-156.
[4]張慧杰,郭志平,司景萍,等.汽車懸架整車動力學(xué)模型的參數(shù)辨識[J].振動與沖擊,2013,32(23):145-150.
[5]HAYASHI Y,TSUNASHIMA H,MARUMO Y.Fault detection of railway vehicle suspension systems using multiple-model approach[J].Journal of Mechanical Systems for Transportation&Logistics,2008,1(1):88-99.
[6]TSUNASHIMA H,MORI H.Condition monitoring of railway vehicle suspension using multiple model approach[J].Journal of Mechanical Systems for Transportation&Logistics,2010,7(3):584-589.
[7]YIN S,LI X,GAO H,et al.Data-based techniques focused on modern industry:an overview[J].IEEE Transactions on Industrial Electronics,2015,62(1):657-667.
[8]WEI X,LIN S,LIU H.Distributed fault detection observer for rail vehicle suspension systems[C]∥Control and Decision Conference,2012:366-383.
[9]YIN S,HUANG Z.Performance monitoring for vehicle suspension system via fuzzy positivistic C-means clustering based on accelerometer measurements[J].IEEEAsme Transactions on Mechatronics,2015,20(5):1-8.
[10]GAO C,ZHAO Q,DUAN G.Robust actuator fault diagnosis scheme for satellite attitude control systems[J]. Journal of the Franklin Institute,2013,350(9):2560-2580.
[11]HAYASHI Y,TSUNASHIMA H,MARUMO Y.Fault detection of railway vehicle suspension systems using multiple-model approach[J].Journal of Mechanical Systems for Transportation&Logistics,2008,1(1):88-99.
[12]YUAN.Application of subspace-based method in vehicle handling dynamic model identification and properties estimation[J].International Journal of Vehicle Design,2011,56(1-4):125-145.
[13]DONG G,CHEN J,ZHANG N.Investigation into onroad vehicle parameter identification based on subspace methods[J].Journal of Sound&Vibration,2014,333(24):6760-6779.
[14]CHEN Z,WANG T,GU F,et al.The average correlation signal based stochastic subspace identification for the online modal analysis of a dump truck frame[J]. Journal of Vibroengineering,2015,17(4):1971-1988.
[15]OVERSCHEE P V,MOOR B D.Subspace identification for linear systems:Theory[M].NewYork:Kluwer Academic Publishers,2012:149-157.
(編輯:李妮)
Research of method and test for suspension system condition monitoring based on modal parameter identification
LIMiaoshuo1,GU Fengshou2,WANG Tie1,LI Guoxing1,2,WANG Yonghong3,LU Xingchen1
(1.Department of Vehicle Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Centre for Efficiency and Performance Engineering,University of Huddersfield,Manchester HD1 3DH,UK;3.Shanxi Dayun Automobile Manufacture Co.,Ltd.,Yuncheng 044000,China)
The performance of suspension system is directly related to the vehicle safety,riding comfort and handling stability.However,the road surface is a kind of random excitation,which places many difficulties in research on the condition monitoring of suspension system.Based on the average correlation signal based stochastic subspace identification(ASC-SSI),a novel method was presented to identify the modal parameters of suspension system in this article.The average correlation signal based stochastic subspace identification method was used to identify model parameters and the changes in suspension stiffness caused by changes of model parameters are monitored.Firstly,the validation of this algorithm was confirmed in a high damping ratio situation. Then,based on an established seven degree of freedom dynamic model,the modal parameters of suspension system were identified to analyze the influences of excitation from road roughness and strong noise to identification results,and then a monitoring method based on mode shape and modal energy was proposed.Finally,a test scheme using 9-axis MEMS inertial sensor was designed to monitor the normal and faulty condition and verify the validity and feasibility of the proposed method.
modal parameter identification;suspension system;average correlation signal based stochastic subspace identification;condition monitoring;MEMS
A
1674-5124(2017)05-0138-07
10.11857/j.issn.1674-5124.2017.05.029
2016-10-07;
2016-12-05
李苗碩(1988-),男,山西太原市人,碩士研究生,專業(yè)方向?yàn)檐囕v現(xiàn)代設(shè)計理論。

