關節間隙對機械臂末端定位精度的影響研究

許昌瑀，董惠敏，王承剛，田志濤

（1.大連理工大學 機械工程學院，大連 116024；2.大連運明自動化技術有限公司，大連 116000）

關節間隙對機械臂末端定位精度的影響研究

許昌瑀1，董惠敏1，王承剛2，田志濤2

（1.大連理工大學 機械工程學院，大連 116024；2.大連運明自動化技術有限公司，大連 116000）

建立了由關節間隙引起的機械臂末端定位誤差的數學模型并且提出了一種概率的方法聯系單個關節的間隙誤差與機械臂末端定位誤差的關系，并得出末端定位誤差特性。方法中運用了蒙特卡洛模擬，相比解析法的繁雜，蒙特卡洛模擬更為簡單方便，它不僅可得出機械臂末端定位誤差的極限值，而且還能得到末端定位誤差的概率密度分布和分布的一些數值特征。學者研究關節間隙誤差時常見有兩種方法，確定性方法和概率論方法，通過綜合這兩種方法能更好地考慮影響關節間隙誤差方向的主要因素和一些不確定性因素。 最后數值舉例闡述了這一思路。這些工作可為機器人設計和工作位點規劃提供一個參考并能有效的平衡精度需求和經濟效益。

關節間隙；蒙特卡洛模擬；工業機器人；末端定位精度

0 引言

隨著機器人在工業自動化領域的快速發展，國內外學者對機器人的精度和特性研究越來越重視。其中，定位精度是機器人一項很重要的特性。影響定位精度的因素很多，其中很主要的一個因素就是關節間隙。對于絕大多數機構，關節間隙是不可避免的，比如一些加工誤差，磨損，裝配誤差以及軸承間固有間隙都導致關節間隙的出現。不像由制造加工或者是機械臂變形引起的系統結構誤差可以通過標定之后補償抵消，低重復性的關節間隙誤差引起的定位誤差具有隨機性很難補償抵消。對于關節間隙，一些學者研究其產生的動力學影響比如由關節間隙引起的接觸力，間隙間碰撞和振動等等[5,8]。還有一些學者關注其產生的運動學影響包括機構精度的評估，機械臂的重復定位精度以及機械臂末端誤差的數學模型[2～4,6,7,9～11]。現在主流有兩種方法來研究關節間隙引起的運動學問題：確定性方法和離散性方法。確定性方法主要是通過假設的接觸力模型來確定關節間隙內接觸點從而確定關節間隙誤差大小和方向而離散的方法主要是從概率論的方法來處理這個不確定因素問題。

研究各個關節間隙誤差在傳動鏈下累積到末端的定位誤差時，Innocenti, C.[2]提出了一種基于虛功而得到各關節間隙誤差和產生的末端定位誤差的關系。之后Stefano,V.和Vincenzo, P. C.[9]進一步完善了這種方法。有些學者則運用幾何的方法來得到末端的極限定位誤差比如Ting, K. L.和Tsai, M. J.[10]做的工作。而對于一些結構簡單的特定的機器人機構，一些學者直接應用坐標變換的方法來得到末端的定位誤差模型（由關節間隙引起的誤差），比如Jawale,H.P.[3]用這種方法分析研究了一個五連桿平面機械臂。Nicolas, B.[6]提出了一個系統的應用坐標變換來研究機械臂末端定位誤差的方法。

在考慮關節間隙引起的運動學問題時多數學者研究機械臂末端產生的極限誤差用此來保證允許的最大定位精度[6,10]。也有一些學者研究在工作空間內的合理的軌跡規劃，即當存在關節間隙時怎樣合理規劃工作軌跡能降低和最小化末端的偏差[4,7]。極值的研究確實很重要，但事實上定位誤差到達極值附近的概率非常小。應用概率的方法不僅能得到誤差的極值還能得到定位誤差的概率分布以及一些數值特征，為更好的達到設計時機械臂的精度需求和經濟效益的平衡提供參考。

1 定位誤差模型的建立

3-DOF串聯型工業機械臂廣泛應用在多個工業領域，如焊接，噴涂，搬運等，常見結構如圖1所示，相應機構簡圖如圖2所示。定義坐標系B0為基底坐標系，機械臂各臂桿坐標系為Bi，i=1，2，3，Oj為坐標系Bj（j=0，1，2，3）原點，坐標原點位于各關節軸線上，臂桿長度為li，臂桿1,2,3位于同一平面α。zi軸沿著R為關節的軸線方向，x1軸在平面α內并垂直于z1軸，x2，x3軸沿著臂桿2,3方向。定義h為O0到O1的高度，θc定義為x1軸和臂桿l1之間的角度，為固定常量。θi（i=0,1,2）微關節i的旋轉角。θ1，θ2為軸xi+1到臂桿li的角（逆時針為正）。

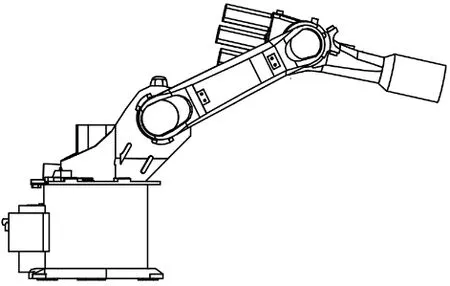
圖1 3-DOF串聯式機器人

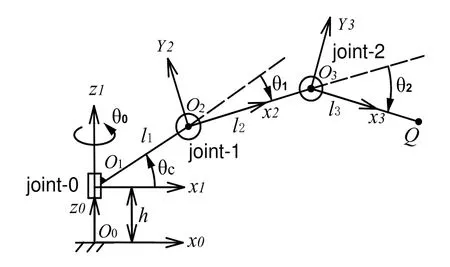
圖2 機構運動簡圖

上述給出了沒有關節間隙的理想運動簡圖。事實上，關節間隙是不可避免的，考慮關節間隙時，暫且只考慮轉動關節存在的間隙尺寸誤差忽略間隙之間的形狀誤差并假設軸孔之間連續接觸，當只研究機械臂末端的定位誤差而不考慮它的姿態誤差時（工業機器人姿態一般由末端機械手的三自由度保證），可假設軸與孔的軸線平行。由此關節間隙誤差ε可以簡化為一個平面向量，其大小是一個常數ε=R-r（軸孔半徑差），方向θε可如圖3定義。機構簡圖如圖4所示。

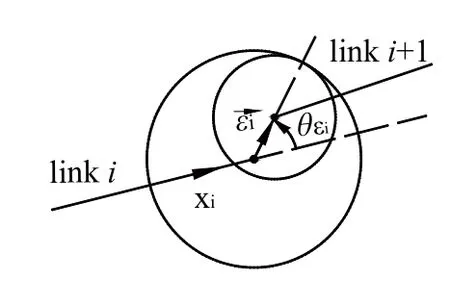
圖3 關節間隙誤差向量

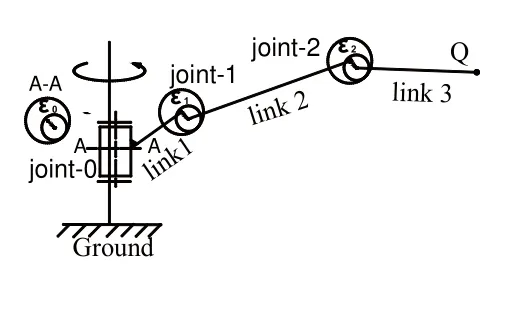
圖4 機構簡圖（存在關節間隙）

用εi和θεi分別表示關節i的間隙誤差大→小和方向，其中θεi定義為坐標軸xi指向間隙誤差向量i的角（逆時針為正），i=0,1,2。考慮機械臂末端點Q，應用坐標變換由圖二得 ，B0PQ和B3PQ分別為Q點在基底坐標B0和臂桿坐標B3下的坐標表示，其中是從B到B的坐標變換矩陣，其中ii-1旋轉（θx,i-1,i，θy,i-1,i，θz,i-1,i），平移（xO,i-1,i，yO,i-1,i，zO,i-1,i），因此機械臂末端Q點的定位誤差為：

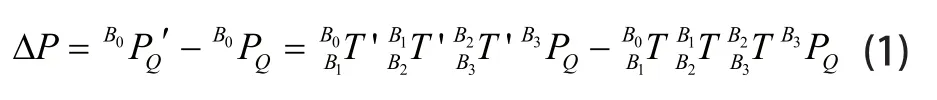
變換矩陣分別為：

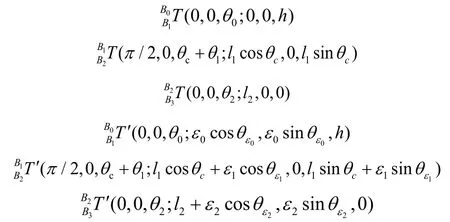
代入式(1)可得機械臂末端定位誤差的數學模型：

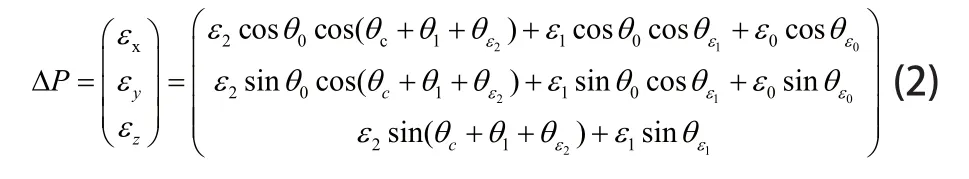
對于給定的工作位點，θc，εi和θi給定。因此，模型變量只有θεi。由式(2)可解析求出末端x,y,z方向上定位誤差的極大值。

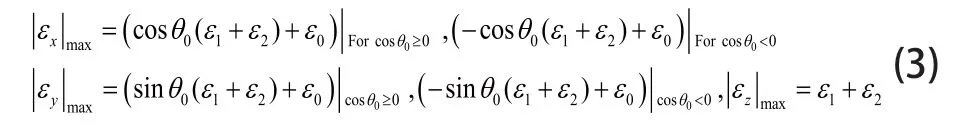
若用空間距離d來評估定位偏差，即定義d2=εx2+εy2+εz2。有：

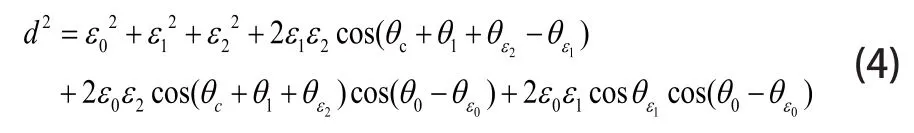
上式非常復雜很難通過解析方法來得到它的最大最小值。并且解析法無法求出誤差的數值特征，一種通過概率的隨機模擬方法可用來得到它的最值及分布。

2 概率方法得到定位誤差分布

當工作位點確定時，機械臂末端定位誤差的x-y-z方向最大值可由式(3)分析得到，但事實上，誤差到達最大值附近區域的概率很小。因此研究機械臂末端定位誤差的分布能更全面的反映隨機誤差特性。

由于誤差模型函數很復雜，即使知道單個關節的間隙誤差特性，也很難通過解析方法得到末端定位誤差的數值特征和分布。運用蒙特卡洛模擬的概率抽樣方法可解決這一問題。蒙特卡洛是一種建立在大數定理和中心極限定理的數學原理上的一種隨機模擬方法。基本思想如下，對于一個函數Y=f（X1，X2，…，Xn），已知自變量X1，X2，…，Xn的概率分布，首先根據X1，X2，…，Xn的概率分布隨機抽樣出一組值x1，x2，…，xn。代入到函數式求得變量Y的一個值yi=f（x1i，x2i，…，xni)。大量重復這一過程（i=1，2，…，m）即得到變量Y的一組樣本y1，y2，…，ym。當重復抽樣次數m足夠大，模擬得到的變量Y的樣本中的數值信息就能非常精確的代表實際變量Y的分布及數值特征。

由節2可知，變量εx, εy, εz, d是θεi的函數（參數θc, θi, εi為常量），i=0，1，2。以下闡述應用蒙特卡洛模擬的方法來分析機械臂末端定位誤差的流程：

1）給定工作點，代入常量參數θc，εi和θi的參數值到式(2)中的誤差模型，再根據需求給定合適的抽樣次數m，通常m=106能給出95%以上精確度，隨著抽樣次數m的增多，蒙特卡洛模擬結果更加精確。

2）確定輸入變量θεi的分布類型，簡單的假設是，關節間隙的誤差方向角θεi可能服從0-2π的均勻分布或者其他分布如正態分布等。再根據每個輸入變量的概率分布隨機抽取m組樣本值θεi,r,（i=0，1，2；r=1，2，…，m）。

3）依據模擬抽取的輸入變量的樣本值（θε0,r, θε1,r, θε2,r）和節2中的函數關系計算出變量εx，εy，εz，d的m組樣本值。

4）依據輸出變量的樣本值得出機械臂末端定位誤差的分布以及數值特征。

3 分析間隙誤差方向概率分布的聯合方法

影響關節間隙誤差方向因素很多，甚至有些因素的本身就不確定。因此完全確定性的分析很復雜也很難得到，而完全概率的方法往往忽略了一些主要因素的影響，比如載荷，重力等臂桿受到的總外力。結合確定性和概率的方法在這一節被引入。首先結合機械臂桿受到的外力與關節間隙作用力（正壓力忽略不確定因素）的力平衡得到關節間隙軸與孔的接觸點，然后在這個間隙誤差方向（即θεi）上建立一個正態分布來表示其他微小不確定性的因素擾動，如轉動關節間隙內產生的摩擦力，碰撞，彈性變形等。

3.1 力平衡得到關節間隙內軸與孔的理想接觸點

考慮機械臂所受外力與軸孔之間作用力的力平衡。暫時忽略軸孔之間一些細微不確定因素，如彈性變形，碰撞和摩擦力等，只考慮關節間隙內的正壓力FN。因此正壓力FN可從力平衡方程中求得。

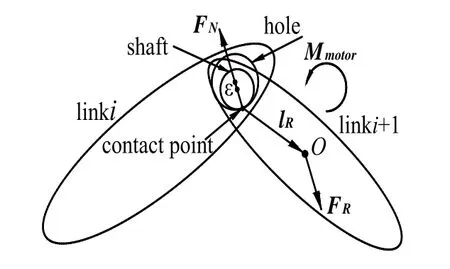
圖5 關節處的受力平衡

如圖5所示，可從力平衡關系得到：

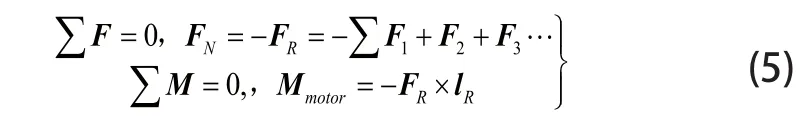
不考慮軸孔間作用的其他因素時，FN方向通過接觸點以及軸孔的圓心，即FN方向為關節間隙誤差方向的反方向。由于臂桿所受的外合力產生的外力矩將被電機和傳動機構產生的扭矩平衡，因此事實上只需考慮力的平衡即可得到正壓力方向。從而得出間隙誤差方向，得到的間隙誤差方向角記為θb。

以上忽略了軸孔間微小摩擦力及一些其他微小不確定量，如碰撞，振動，彈性變形等。這些微小因素會在上述得到的接觸點附近產生一些擾動。首先，通過上述方法得到接觸點，然后可用一個誤差分布來引入其他微小擾動，使分布的平均值為θb，標準差來表示引入的微小擾動。

3.2 正態分布引入擾動

影響間隙誤差方向的微小隨機因素很多，如摩擦力，瞬時碰撞，彈性變形，潤滑油膜等等。根據概率論中的中心極限定理，當影響一個變量的隨機因素很多時，該變量的分布近似于一個正態分布，因此可依據上節得到的接觸點建立一個正態分布來擬合這些微小因素。記間隙誤差方向分布為θε～N（θb，σ2），θb為上節由力平衡得到的間隙誤差方向。σ為正態分布的標準差。σ表示微小因素的擾動。具體值可由關節精密等級和具體工況經驗性得出。

4 具體數值計算

考慮如圖1所示的三自由度機械臂機構為對象來闡述上述方法（蒙特卡洛模擬）來研究機械臂關節間隙對末端定位精度的影響。設定常量參數值ε0=0.5，ε1=0.4，ε2=0.3，θc=π/4，選定一個工作位置，θ0=π/5，θ1=-π/6，θ2=-π/4。選擇抽樣次數m為一般值106。以下先假設關節間隙誤差方向θεi服從均勻分布（即完全隨機）來舉例闡述上述的概率方法。再代入第3節所闡述的綜合思路中的正態分布。

1）假設關節間隙誤差θε0，θε1，θε2為均勻分布

將θε0，θε1，θε2為均勻分布代入節3的流程可得末端定位誤差εx，εy，εz和d的概率密度函數，以下概率密度函數已由“核估計”法擬合光滑。

一些數值特征可從蒙特卡洛模擬中得出。x方向的最大定位誤差|εx|max=1.066，與用解析法求得的|εx|max=cosθ0（ε1+ε2）+ ε0=1.066一致，驗證了蒙特卡洛模擬的精確性。同時還可得出解析法無法求出的數值特征，如標準差σx=0.257，誤差分布的上95%分位點為0.861，這也意味著在95%的可信度下，x方向的定位誤差的范圍為0～0.861而不是0～1.066。由此能更好的評價末端定位誤差值。同樣可得y方向，z方向和空間距離d的數值特征。關節間隙誤差方向角若服從均勻分布，由圖6(c)可看出隨著θ0，θ1的變動，空間距離d的數值特征保持不變，即工作位置對末端定位誤差的空間距離沒有影響。

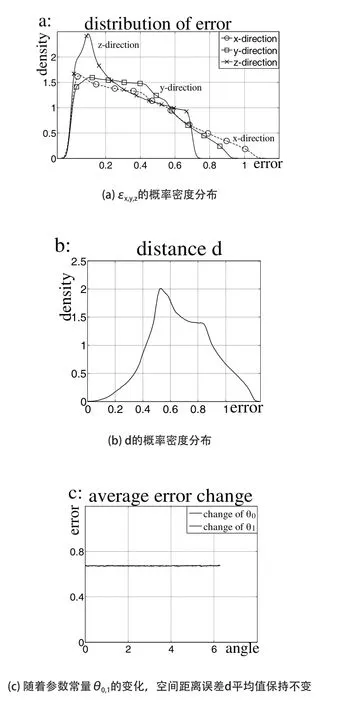
圖6 概率密度函數圖

2）代入上節得到的正態分布

為了闡述方便，只考慮作用在力臂上的兩個主要的力，重力和運動的離心力。如圖1、圖2所示機構，機械臂常量參數設定不變，每個關節轉動的角速度分別為ω0=0.5rad/s，ω1=4rad/s，ω2=6rad/s。臂桿2，3的質心到1和2關節的孔軸線距離分別為r2=0.3m，r3=0.2m。臂桿2和3質量分別為m2=15kg，m3=10kg。當對關節0運用力平衡來得到關節間隙誤差角θb時，重力是一個向下的力，與關節軸線平行，在不考慮姿態誤差時，對關節間隙誤差方向沒有影響，因此θε0=θ0=π/5（可由離心力方向得出）。給定所有關節的擾動項σ=3°?。

關節1和2，離心力Fcentri=mω2r和重力G=mg。由力平衡計算間隙誤差方向角可得到θε1=-63.312?°，θε2=-80.048?°（詳細計算已省略）。因此各關節間隙誤差方向分布為：

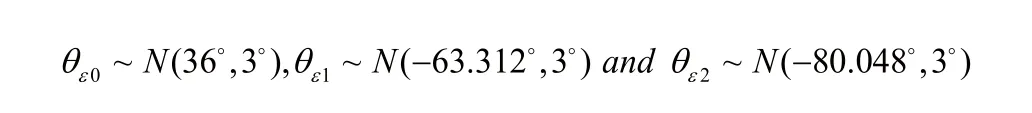
代入第2節流程，運用蒙特卡洛模擬得到末端誤差的概率密度分布如圖7所示。

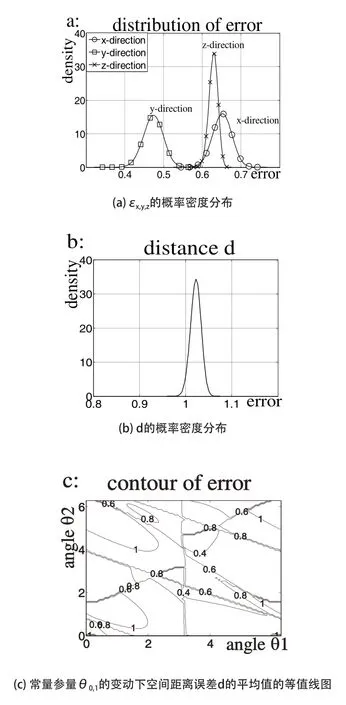
圖7 末端誤差的概率密度分布圖

顯然，這種綜合思路可以得到的末端定位誤差分布范圍更狹窄，意味著可估計出更精確的定位誤差值。相比完全隨機的均勻分布時工作位點對末端定位精度沒有影響，這種綜合思路，參數常量θ1，θ2的值的變動會對末端的定位誤差產生很大的影響，意味著通過合理規劃工作位點可降低由關節間隙引起的末端定位誤差。如圖8(c)等值線圖所示，當合理選擇θ1和θ2的值時，末端定位誤差d的平均值可從1降到0.4。通過這種規劃可以很好地提高機械臂的重復定位精度而不需要更好的設備投入，如精確等級更高的關節。

5 結論

首先建立了存在關節間隙時一個三自由度機械臂末端定位精度的數學模型，然后運用蒙特卡洛的方法得到機械臂末端定位精度的分布和一些數值特征。運用這種方法可以得到更加全面的分布特征如誤差最大值、平均值、方差和誤差的上95%分位點等。一種綜合的思路更好的考慮了影響關節間隙誤差方向的主要因素和細小擾動因素，以一個分布來擬合表示那些不確定因素的擾動。這種方法可得出一個范圍更加狹窄更加精確的末端定位誤差分布并可通過合理規劃工作空間以很好地提高機械臂的重復定位精度而不需要投入精確等級更高的關節。

[1] Flores, P., A parametric study on the dynamic response of planar multibody systems with multiple clearance joints[J].Nonlinear Dynamics, 61(4), 633-653(2010).

[2] Innocenti, C., Kinematic Clearance Sensitivity Analysis of Spatial Structures with Revolute Joints[J].ASME, Design Engineering Technical Conference, Paper DETC98/DAC-8679,1999.

[3] Jawale, H. P. andThorat, H. T., Investigation of Positional Error in Two Degree of Freedom Mechanism With Joint Clearance[J]. ASME, J. Mech. Rob. 2012.

[4] Lai Ming-Cheng and Chan Kuei-Yuan, Minimal deviation paths for manipulators with joint clearances[J].ASME, Mechanisms and Robotics Conference pp.V05BT08A058,2014.

[5] Megahed, S.M. and Haroun, A.F.,Study of the dynamic performance of mechanical systems with multi-clearance joints[J]. ASME, IMECE November 12-18,2010.

[6] Nicolas B., Philippe C., Stéphane C.,The kinematic sensitivity of robotic manipulators to joint clearances [J].ASME, Computers and Information in Engineering Conference,2010.

[7] Sel?uk and Erkaya, Trajectory optimization of a walking mechanism having revolute joints with clearance using anfis approach [J], Nonlinear Dynamics,71(1-2)：75-91,2013.

[8] Sony, C., Paulo, F. H. and Hamid, M. L., Computational and Experimental analysis of mechanical systems with revolute clearance joints [J], ASME, IDETC/CIE 2013 August 4-7,2013.

[9] Stefano, V. and Vincenzo, P. C., A New Technique for Clearance Influence Analysis in Spatial Mechanisms[J].ASME J.Mech. Rob. Montreal, Quebec, Canada,2002.

[10] Ting, K. L., Zhu, J. M. and Watkins, D.,The effects of joint clearance on position and orientation deviation of linkages and manipulators [J], Mech. Mach. Theory, 35(3)：391-401,2000.

[11] 張志雄,江志新,楊擁民,等.關節對中誤差對機械臂末端定位精度影響[J].國防科技大學學報,2014,06：185-190.

Study on kinematic positioning error of manipulator caused by joint clearance

XU Chang-yu1, DONG Hui-min1, WANG Cheng-gang2, TIAN Zhi-tao2

TP242.2

：A

：1009-0134(2017)05-0044-05

2017-03-10

遼寧省科技創新重大專項（2015106007）；國家科技重大專項（2013ZX04003041-6）

許昌瑀（1994 -），男，湖南衡陽人，本科，研究方向為機器人。