動力總成懸置系統設計開發

劉通，盧頔，劉立國，王丹

（華晨汽車工程研究院，遼寧 沈陽 110141）

動力總成懸置系統設計開發

劉通，盧頔，劉立國，王丹

（華晨汽車工程研究院，遼寧 沈陽 110141）

動力總成在工作過程中產生的激勵以及路面激勵是汽車振動的主要來源，特別是與解耦計算的關系十分緊密。文章以某車型為研究對象，根據坐標系變換關系，推導出不同坐標系變換矩陣；通過建立ADAMS仿真模型，對懸置系統模態及解耦率進行了分析及優化。仿真分析表明：經過剛度匹配，降低了支撐處動態支反力幅值；最后，通過實車測試，再次論證了解耦設計使整車性能得到了提升。

激勵；坐標變換；解耦；支反力

CLC NO.: U462.33 Document Code: A Article ID: 1671-7988 (2017)10-38-04

前言

隨著汽車技術的不斷提升和完善，乘坐舒適性越來越受到人們的關注。汽車振動又是重要影響因素：一方面來自路面的激勵[1]，另外一方面來自發動機自身的激勵[2]；為此，懸置系統的優化匹配就顯得尤為重要，特別是懸置系統的布置和解耦頻率的設計尤其重要[3-4]。

在懸置系統的設計開發領域，呂振華等[5]通過分析汽車懸置系統的布置方式特性，總結了如何以撞擊中心理論為依據對各個懸置點進行布置以提高汽車的舒適性，另外還進一步闡述了采用V型布置以提高怠速隔振性能的可能性。上官文斌等[6]基于試驗設計方法，計算了懸置剛度對于懸置固有頻率和解耦率的貢獻率。

本文以某項目開發為實例，首先從系統布置角度進行設計，其次通過ADAMS建模，優化解耦頻率，通過支反力的改善來降低振動能量的傳遞[7-8]，最后通過實車測試得到了很好的驗證。

1、坐標系轉換

在動力總成坐標轉換時，采用如圖1定義測量坐標系方式，以發動機曲軸投影到后端面的中心為測量原點，X正向指向發動機方向，Z軸正向垂直剛體上表面指向油底殼，Y軸正向依據右手定則判定。

圖1 坐標系定義Fig.1 Definition of coordinate system

測量坐標系與整車坐標系為在同一點的兩個坐標系，其轉換關系如圖2所示：整車坐標系為O_XYZ坐標系，O_X’Y’Z’為測量坐標系，ON為兩個平面的交線，OX與ON夾角為α，Z與Z’夾角為β，OX’與交線ON夾角為γ，當整車坐標系分別繞Z轉動α，繞X轉動β，繞Z’轉動γ，就會得到測量坐標系。

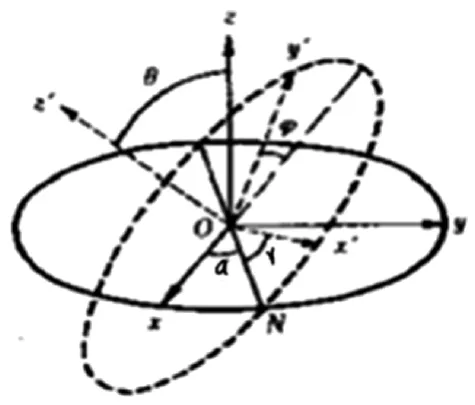
圖2 坐標轉換Fig.2 Coordinate transformation

其中坐標變換矩陣分別為：

當有了總坐標轉換矩陣，依據坐標變換公式即可以求出質心及轉動慣量在整車下的坐標。

2、懸置系統布置設計

在系統選型布置設計初期，我們考慮了行業內幾種常用的布置形式，如圖3所示。

可以看到，在橫置動力總成布置領域，擬合線下方為擺動支撐式布置，這種在行業內最為普遍，易于空間布置和后期調校，因此我們也選用了這種布置形式。

當沿著任意方向給一個自由剛體施加一個扭矩時，該剛體發生轉動所圍繞的軸線即為扭矩軸。

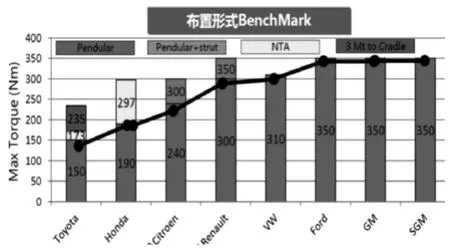
圖3 懸置系統布置形式Fig.3 Layout form of mounting system

在設計過程中，當得到了發動機質心及轉動慣量，懸置在車身上的彈性中心點后，就可以計算扭矩軸與彈性軸的位置關系。一般行業內通過動力總成質心到彈性軸距離以及彈性軸與扭矩軸夾角作為衡量指標，計算結果如圖4和圖5所示：

圖4 扭矩軸俯視圖Fig.4 Vertical view of torque axis

圖5 扭矩軸后視圖Fig.5 back view of torque axis

通過計算，可以看到在圖4中質心到彈性軸距離3mm，兩軸線夾角約3.9°，在圖5中兩軸線夾角1.8°。從結果看俯視圖兩個指標略大，但可以接受。但車身姿態有一定影響，由于總布置因素，硬點位置不好更改，這就需要從懸置剛度調節入手，優化性能參數。

3、懸置剛度設計

3.1 動力學模型建立

動力總成具有6個方向的自由度，并與三個懸置彈性連接，在仿真分析時一般將振動系統簡化為一個無阻尼自由振動系統，其橡膠襯套均附以線性剛度支撐，為此建立模型如圖6。

動力總成懸置系統要綜合考慮路面激勵以及發動機激勵，為此基于以上兩種工況考慮，帶入某項目實際數據，進行設計及優化。

圖6 懸置系統仿真模型Fig.6 Simulation model of mounting system

3.2 懸置系統固有特性分析

通常情況下，來自路面的激勵一般小于4Hz，所以動力總成模態頻率一般大于5Hz為好；而根據簡諧支撐激振下振動響應的特性，頻率比至少需要大于1.414倍才具有隔振效果，本文的研究對象其動力總成怠速轉速在750r/min，即2階激振頻率為25Hz，所以動力總成固有模態頻率上限不應大于17.68Hz。

根據表1，由初始設計剛度可以計算六階固有頻率和解耦率，見表2：

Table 1 Mounting stiffness

表1 懸置剛度

表2 固有頻率和解耦率Table 2 Natural frequency and decoupling rate

在解耦率方面，根據動力總成的振動特性，垂向Z與俯仰方向為振動的主方向，因此這兩項指標要同時達到90%以上才符合要求，其他方向非振動主要方向，達到85%即可。由表2可知，俯仰方向解耦率僅為77%，非常差，與橫擺存在8%的耦合，在這兩個頻率段振動時會耦合振動，使整車舒適性受到很大影響。而在頻率方面，X向與Z向耦合嚴重，其頻率間隔僅僅0.1Hz，這在振動時共振會比較明顯，大大增加了懸置隔振的難度，設計時最好滿足1Hz間隔會比較好。而側傾頻率達到18.3Hz也大于我們要求17.7Hz的上限，懸置不在隔振區。

綜上，根據實際樣車的剛度匹配計算分析，進行剛度優化和改進是十分必要的。

3.3 懸置系統優化設計

3.3.1 剛度優化分析

通過仿真計算分析得到符合要求的剛度值和模態分布，見表3和表4：

表3 懸置剛度Table3 Mounting stiffness

表4 動力總成懸置系統固有頻率和解耦率Table 4 Natural frequency and decoupling rate

從優化后的固有頻率和解耦率可以看到，總體頻率分布為7.1～16.2Hz，且頻率間隔達到了1Hz。解耦率方面，Z向達到96.5%；俯仰方向由77%提升到了93%，同樣達到了很好的效果。

3.3.2 動態支反力優化

衡量剛度是否匹配合適，懸置支撐處動反力大小也能體現隔振性能。

根據發動機外特性曲線，采用函數逼近方式來近似模擬發動機怠速激勵振動。某項目動力總成怠速750r/min，在Adams模型質心處，分別施加沿氣缸垂直振動方向激勵：cos(25*πt)；與繞曲軸方向激勵：80sin(25*πt)來模擬怠速激勵振動。

圖7 優化前動態支反力響應圖Fig.7 Dynamic reaction force response before optimize

圖8 優化后動態支反力響應圖Fig.8 Dynamic reaction force response after optimize

在怠速振動時，由于初始激勵的作用，是由瞬態逐漸過渡到穩態的過程。為此我們針對解耦剛度匹配前后，觀察發動機懸置動態支反力的變化，由圖7可以看到，在8s以后，模型基本達到了穩態振動，其中最大處反力達到1436N，這里包含了1050N預載的作用，因其初始匹配剛度不是太理想，俯仰方向作為振動主方向解耦率低，耦合較為嚴重，在反力的體現上也是比較明顯。

經過剛度優化后，可以看到如圖8，同樣在預載情況下，8s以后最大動態支反力峰值為1112N，這是由于合適的剛度匹配后，俯仰解耦率很高，基本不存在和其他方向的耦合振動，所以支反力減小了很多。支反力減小了，傳遞到車身上的振動隨之減小，也就是我們常說隔振更好了。

4、實車測試驗證

通過仿真分析，剛度優化使得懸置系統的隔振性能得到了明顯改善和提高。但是由于仿真分析的準確性還是與實際有誤差，故需要進行實車的NVH驗證[9]。

本文中，實車測試選取了點熄火工況進行測試，點熄火工況可以很好的驗證懸置系統剛度匹配情況。本文在人體感受最為明顯的座椅導軌處安裝加速度傳感器對振動響應進行測試和對比[10]。

在圖9中，可以看到點熄火是一個瞬態工況，加速度峰值時間非常短， 圖中在4.39s達到最大峰值1.28m/s2，而在圖10中，通過優化懸置三向剛度的比例，可以看到最大峰值優化到0.75m/s2。這是由于動力總成懸置系統點熄火工況取決于懸置剛度匹配好壞，特別是X向剛度合力優化。

圖9 優化前座椅X向加速度Fig.9 Acceleration of seat in X direction before optimize

圖10 優化后座椅X向加速度Fig.10 Acceleration of seat in X direction after optimize

綜上，通過實車測試，再次論證了懸置剛度設計匹配的重要性。

5、結論

本文通過坐標轉換矩陣的推導給出了坐標轉換的公式；通過扭矩軸布置設計給出合理的安裝位置；通過解耦匹配及優化提高了隔振性能及主觀感受。研究結果表明：

1）坐標轉換是懸置系統設計的前提和基準，精確的轉化才能提高系統布置的準確性，為后續的剛度匹配提供便利。

2）通過懸置剛度的匹配，使得懸置的隔振性能得到提高，發動機懸置動態支反力由1436N降低到1112N。

3）實車測試表明：合理的剛度匹配能夠提升駕駛員的主觀感受，即發動機點火加速度由1.28m/s2降低到0.75m/s2。

[1] 徐石安. 汽車發動機彈性支撐隔振的解耦方法 [J] 汽車工程, 1995,17(4):198-204.

[2] Tamboli J A,Joshi S G. Optimum design of a passive suspension system of a vehicle subjected to actual random road excitations[J]. Journal of Sound and Vibration,1999,219(2): 193-205.

[3] SJOBERG M.Robber Isolation-Measurements and Mmodelling Using Fractional Derivatives and Friction[R]. SAE 2000,1-3518.

[4] GARCLA-TARRAGO M J,KARIL.Frequency and Amplitude Depen -dence of the Axial and Radial Stiffness of Carbon-Black Filled Rubber Bushing[J].Polymer Testing,2007(26)：629-638.

[5] 呂振華,范讓林,馮振東,汽車動力總成隔振懸置布置的設計的思想論析[J]. 內燃機工程,2004.3(25):37-43.

[6] 上官文斌,呂振華. 液阻型橡膠隔振器非線性特性仿真分析[J].振動工程學報,2003, 16(4):393-398.

[7] Li Wei,Wang Dengfeng,Chen Shuming,et al. Transfer path analysis of powertrain vibration on drive’s noise[J]. ICNC,2011,4(7):2353-2357.

[8] Karl Janssens,Peter Gajdatsy,Ludo Gielen,et al.OPAX:A new transfer path analysis method based on parametric load models[J].MSSP, 2011,25:1321-1338.

[9] 梁天也,史文庫,唐明祥. 發動機懸置研究綜述[J].噪聲與振動與控制,2007,1:6-10.

[10] 呂兆平 楊曉 秦際宏. 某微型車駕駛室座椅導軌怠速異常振動分析與改進[J]. 汽車技術, 2012, 447(12): 47-50.

Design and development of Powertrain Mounting System

Liu Tong, Lu Di, Liu Liguo, Wang Dan
( Brilliance Auto R & D Center (BARC), Liaoning Shenyang 110141 )

Road excitation and engine excitation are the main sources of Automobile vibration. Especially closely related to decoupling. Based on a car as the research object, the coordinate transformation matrix is derived according to the coordinate transformation. A simulation model of ADAMS is established, and the decoupling rate and modal of powertrain mounting system is analyzed. Simulation analysis shows that: dynamic force is reduced through matching stiffness. Finally, by means of the car test, the results indicate that the vehicle performance is improved through decoupling design.

excitation; coordinate transformation; Decoupling; reaction force

U462.33

A

1671-7988 (2017)10-38-04

10.16638/j.cnki.1671-7988.2017.10.014

劉通(1984-)，男，工程師，碩士，就職于華晨汽車工程研究院，研究方向：動力總成懸置系統開發及優化。