基于近紅外光譜技術的針葉材板材表面節子缺陷檢測

周 竹， 尹建新， 周素茵， 周厚奎

（1.浙江農林大學 信息工程學院，浙江 臨安 311300；2.浙江農林大學 浙江省林業智能監測與信息技術研究重點實驗室，浙江 臨安311300；3.浙江農林大學 智慧農林業研究中心，浙江 臨安311300）

基于近紅外光譜技術的針葉材板材表面節子缺陷檢測

周 竹1,2,3， 尹建新1,2,3， 周素茵1,2,3， 周厚奎1,2,3

（1.浙江農林大學 信息工程學院，浙江 臨安 311300；2.浙江農林大學 浙江省林業智能監測與信息技術研究重點實驗室，浙江 臨安311300；3.浙江農林大學 智慧農林業研究中心，浙江 臨安311300）

為了實現木板材依據節子進行自動化分級，采用近紅外光譜技術研究了多種針葉材表面節子缺陷的檢測方法。采用SmartEye 1700近紅外光譜儀獲取北美黃杉Pseudotsuga menziesii，鐵杉Tsuga chinensis，云杉Picea asperata，白云杉Picea glauca-英格曼云杉Picea engelmannii-扭葉松 Pinus contorta-冷杉 Abies laciocarpa（SPF）等 4種板材的近紅外光譜（1 000～1 650 nm），比較了光譜預處理方法、建模方法對節子識別的影響，并首次對多種針葉樹材進行了節子識別的適應性研究，隨后引入一種新的變量選擇方法即隨機青蛙算法用于優選節子檢測的特征波長，在此基礎上建立了板材節子識別的最小二乘-支持向量機（LS-SVM）模型。結果顯示：一階導數光譜預處理結合LS-SVM所建混合樹種板材節子識別模型性能最優。隨機青蛙算法提取了8個特征波長變量，僅占全波段變量的1.23%，所建簡化模型效果最好。該模型對測試集的敏感性、特異性和識別準確率分別為98.49%，93.42%和96.30%。近紅外光譜技術結合化學計量學方法可以對針葉材樹種板材的表面節子進行快速準確檢測，隨機青蛙算法是提取板材表面節子缺陷特征的有效方法。該結果可為下一步搭建木材節子快速檢測系統提供技術支撐。圖2表4參24

木材科學與技術；近紅外光譜；針葉材；板材；節子；隨機青蛙算法；最小二乘-支持向量機

節子是木板材最重要的表面缺陷，它會影響鋸材和單板的出材率、成品質量和表面美觀性［1］。研究一種板材表面節子缺陷快速無損檢測方法，不僅可以提高木材的利用率和經濟價值，而且可為木板材的自動化分級奠定基礎。近幾年來，研究人員采用聲波技術［2-3］、微波技術［4］、X-射線技術［5-6］、機器視覺技術［7-8］等對木材表面節子缺陷進行了一系列無損檢測研究。然而，如何提高板材節子缺陷檢測的快速性、準確性以及對不同樹種板材的適應性仍有待深入研究。近紅外光譜技術（near-infrared spectroscopy, NIRS）利用近紅外光譜區域的全譜或部分波譜對被測物進行無損快速分析。迄今為止，該技術已在快速預測木材化學組成［9］、物理力學性質［10］、解剖性質［11］、木材腐朽［12］等方面進行了大量的研究。在木材表面節子缺陷檢測方面，FUJIMOTO等［13］將近紅外光譜與簇類獨立軟模式法（soft independent modeling of class analogy,SIMCA）結合，建立了落葉松Larix kaempferi板材節子分類識別模型。楊忠等［14-15］利用近紅外光譜技術結合SIMCA分別建立了馬尾松Pinus massoniana板材、尾葉桉Eucalyptus urophylla板材節子識別模型。上述研究均僅采用單一樹種板材。由于木材種類繁多，木材種屬、紋理等多種因素會引起板材光譜差異，從而影響節子缺陷檢測模型的適應性。此外，近紅外光譜變量較多，直接使用全部變量會影響識別的速度與精度，需對光譜數據進行降維。本研究擬采用近紅外光譜技術檢測北美黃杉Pseudotsuga menziesii，白云杉Picea glauca-英格曼云杉Picea engelmannii-扭葉松Pinus contorta-冷杉Abies laciocarpa（SPF），鐵杉Tsuga chinensis和云杉Picea asperata等4類常見針葉林樹種板材的表面節子缺陷，比較不同光譜預處理和建模方法對節子識別的影響，研究單一樹種板材節子模型對其他樹種板材節子缺陷檢測的適應性，建立混合樹種板材節子缺陷的識別模型，采用隨機青蛙算法（random frog,RF）確定節子缺陷識別的有效特征波段，并建立簡化模型，從而為木板材表面節子缺陷的快速準確識別提供方法與技術支撐。

1 材料與方法

1.1 試驗材料

試驗樣本來自當地木材加工廠，包括北美黃杉、鐵杉、云杉以及進口自加拿大的SPF二級規格材。樣本含水率為7.9%～11.7%，密度為0.394～0.565 g·cm-3。將全部試材切割成200 mm×80 mm×20 mm的單板，在單板上按序標記節子部位并根據GB/T 4822-1999《鋸材檢驗尺寸檢量》記錄節子直徑，同時在板材節子附近隨機標記非節子部位，并將標記部位作為光譜采樣點。試驗共標記1 056個光譜采樣點，其中有節子部位459個，無節子部位597個。

1.2 試驗儀器

試驗用光譜采集設備為微型近紅外光譜儀SmartEye1700（尼邇光電，中國杭州），光譜波長范圍為1 000～1 650 nm，采樣間隔為1 nm。采用直徑為8 mm的光纖探頭在試樣垂直上方采集其表面的近紅外漫反射光譜。掃描50次自動平均為 1條光譜后保存待用。對于各個木材品種的板材光譜，將有節子樣本依據節子直徑以2∶1比例進行劃分，而非節子樣本則采用Kennard-Stone算法［16］以2∶1比例劃分，最終組成校正集和測試集的非節子、節子數目如表1所示。

1.3 光譜預處理方法

采用標準正態變量變換（standard normalized variate，SNV），一階導數（first derivative,FD）等方法對原始光譜（no preprocess,NP）進行預處理。其中，標準正態變量變換可以消除木板表面散射等對光譜的影響，一階導數變換可以有效消除基線和其他背景的干擾［17］。

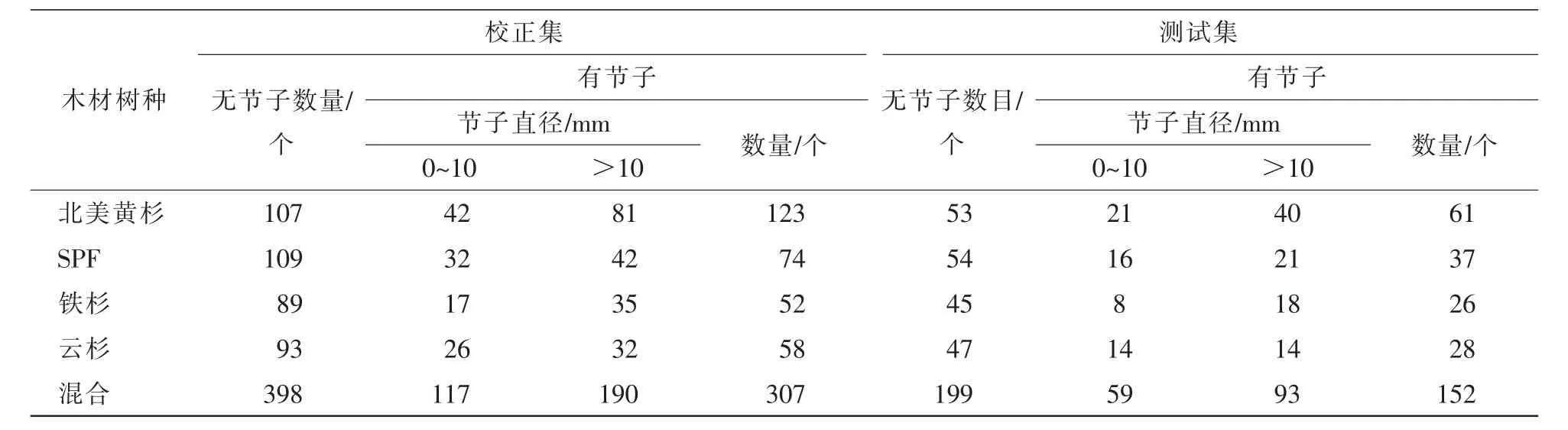
表1 試驗樣本集數據組成信息Table 1 Information of calibration set and validation set in the experiment

1.4 建模方法

分別采用主成分回歸-線性判別分析法（PCA-LDA），偏最小二乘回歸-線性判別分析法（PLS-LDA）和最小二乘-支持向量機法（LS-SVM）建立板材節子識別模型。PCA-LDA和PLS-LDA為線性建模方法，LSSVM為非線性建模方法。3種建模方法的原理分別見文獻［18］［19］和［20］。PCA-LDA方法中主成分數量以及PLS-LDA方法中潛在變量的個數決定了所建模型的性能。本研究采用留一交叉驗證法確定2類模型的參數。采用RBF核函數作為LS-SVM分類器的核函數，并以留一交叉驗證法結合網格搜索算法確定LS-SVM分類模型參數。

1.5 特征波段選擇方法

采用隨機青蛙算法（RF）與PLS-LDA結合進行特征波長選擇。RF算法是由LI等［21］提出的一種新的變量選擇方法。該方法通過少量變量進行迭代建模，是一種高效的多維變量選擇方法。圖1給出了隨機青蛙算法示意圖。其運算過程主要包括［22］：①初始化包含q個變量的初始變量集合為υ0；②基于原始變量子集構造含有q*個變量的候選變量子集υ*，并按一定概率接受υ*，令υ1＝υ*，迭代n次；③計算每個變量的選擇概率，并作為變量選擇的依據。通常，變量的被選概率越大，說明該變量對模型越重要。

1.6 模型評價

模型性能的評價指標包括敏感性、特異性和預測總正確率。其定義為：敏感性（%）＝（預測正確的非節子樣本數/實際非節子樣本數）×100%。特異性（%）＝（預測正確的節子樣本數/實際的節子樣本數）×100%。總正確率（%）＝（預測正確的所有樣本數/實際樣本數）×100%。通常情況下，敏感性、特異性和總正確率越高，說明模型性能越好。

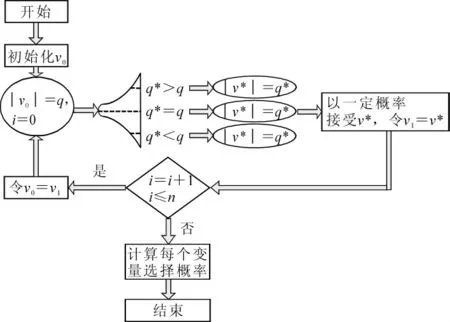
圖1 隨機青蛙算法工作流程圖Figure 1 Key steps of random frog algorithm

2 結果與分析

2.1 板材的光譜分析

圖2為4種板材的非節子和節子部位的平均光譜圖。由圖2可以看出：不同樹種板材的非節子和節子部位的平均光譜均在1 195 nm和1 462 nm附近存在明顯的吸收峰。其中，1 195 nm附近區域包含了木材中纖維素或木質素C—H伸縮振動的二級倍頻信息［23］，1 462 nm附近區域包含了板材中水分或木質素中酚類物質O—H基團伸縮振動的一級倍頻信息［14］。

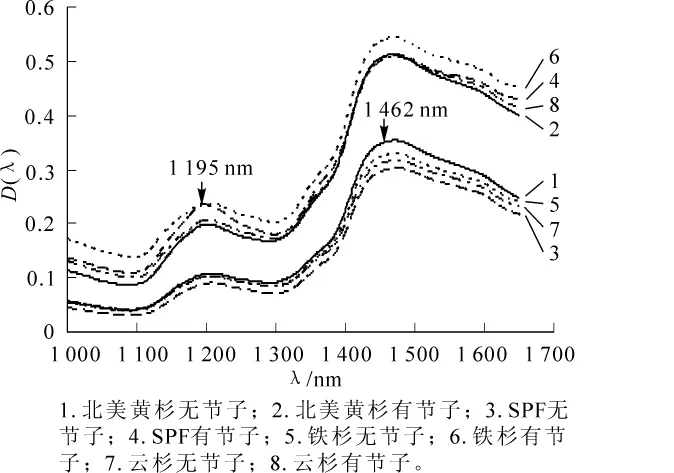
圖2 不同樹種板材節子與非節子平均光譜Figure 2 Mean spectra from different types of board for knot and knot-free

從圖2中還可以看出：4種樹種板材節子部位的平均光譜的吸光度要明顯高于非節子部位，這和前人［13-14］的研究結論相似。其原因可能是板材節子部位和非節子部位的微纖絲取向不同，并且板材節子部位細胞的排布基本上平行于近紅外光入射角。除此之外，不同樹種板材非節子部位的平均光譜存在偏移，這可能是不同品種板材間水分含量、色澤和紋理等綜合引起的。

2.2 不同建模方法對節子識別的影響

分別采用PCA-LDA，PLS-LDA和LS-SVM對原始光譜及各種預處理光譜建立4個樹種板材表面節子缺陷的識別模型，結果如表2所示。

由表2可知：建模方法和光譜預處理方法會對節子缺陷識別造成影響。北美黃杉板材、鐵杉板材和云杉板材均表現為一階導數光譜結合最小二乘-支持向量機（FD-LS-SVM）所建模型性能最優。其中，北美黃杉板材的FD-LS-SVM模型對校正集和測試集的敏感性、特異性和識別準確率分別為 100.00%，100.00%，100.00%和 100.00%，97.30%，98.90%；鐵杉板材的 FD-LS-SVM模型對校正集和測試集的敏感性、特異性和識別準確率分別為100.00%，98.08%，99.29%和99.78%，92.31%，95.77%；云杉板材的FD-LS-SVM模型對校正集和測試集的敏感性、特異性和識別準確率分別為100.00%，100.00%，100.00%和100.00%，96.43%，98.67%。對于SFP板材，FD-LS-SVM模型和SNV-LS-SVM模型對測試集的結果相同，前者對校正集的特異性（99.19%）略低于后者（100.00%），但整體結果仍優于原始光譜下的LS-SVM模型。從表2中還可以看出：無論是否進行光譜預處理，4個樹種板材的PCA-LDA模型、PLS-LDA模型性能均劣于LS-SVM模型。

綜上所述，采用線性建模方法PCA-LDA，PLS-LDA和非線性建模方法LS-SVM建立4個樹種板材節子判別模型時，LS-SVM方法要明顯優于PCA-LDA和PLS-LDA，原因可能是PCA-LDA和PLS-LDA均只能處理板材光譜中的線性相關關系，而LS-SVM則可以充分利用光譜數據中的非線性信息（如水分含量、密度、表面粗糙度、色澤和紋理等），從而獲得較優的預測結果。

2.3 單一樹種模型與混合樹種模型對節子識別的影響

為了探索單一樹種板材節子缺陷識別模型對其他樹種板材節子缺陷識別的適應性，該研究分別采用單一樹種板材節子缺陷識別的LS-SVM模型去預測其他3個樹種的板材缺陷。預測結果如表3所示。

由表3可知：單一樹種板材的節子缺陷識別模型對其他樹種板材的節子識別能力存在差異。對于北美黃杉板材，NP-LS-SVM，FD-LS-SVM模型對SPF，鐵杉和云杉板材的敏感性好，但特異性較差，表明此2種模型對SPF，鐵杉和云杉板材中的節子樣本識別效果較差；SNV-LS-SVM模型雖然對SPF板材的特異性（91.80%）較好，但其敏感性差（73.58%），表明該模型也不能用于預測SPF板材節子屬性。對于SPF板材，NP-LS-SVM，SNV-LS-SVM和FD-LS-SVM模型對北美黃杉板材的識別效果均較差，但對云杉板材都能獲得較好的預測效果。其中，FD-LS-SVM模型的效果最優，該模型對云杉板材的敏感性、特異性和識別準確率分別為100.00%，96.43%，98.67%。同時，該模型對鐵杉板材的識別效果也最好，其敏感性、特異性和識別準確率分別為91.11%，92.31%，91.55%。對于鐵杉板材，NP-LS-SVM模型對SPF和云杉板材的預測能力較好，識別準確率分別達到95.61%和94.67%，FD-LS-SVM模型對云杉板材的識別效果最好，其敏感性、特異性和識別準確率分別為97.87%，96.43%，97.33%。對于云杉板材，NPLS-SVM模型對SPF板材的識別效果最好，其敏感性、特異性和識別準確率分別為100.00%，96.72%，98.25%，FD-LS-SVM模型對SPF板材和鐵杉板材的識別效果也較好，識別準確率分別為97.37%和95.77%。

綜上所述，SPF、鐵杉和云杉中任意單一樹種板材的節子識別模型具有較強的適應性，在一定的光譜預處理下，對另外2個樹種板材的節子缺陷具有較好的識別能力。此3種板材的節子識別模型均不能準確地識別北美黃杉板材的節子缺陷，同時，北美黃杉板材的節子識別模型也不能準確地識別SPF、鐵杉和云杉板材中的節子缺陷。其原因可能是SPF、鐵杉和云杉的材性差異較小，但與北美黃杉的材性差異較大。

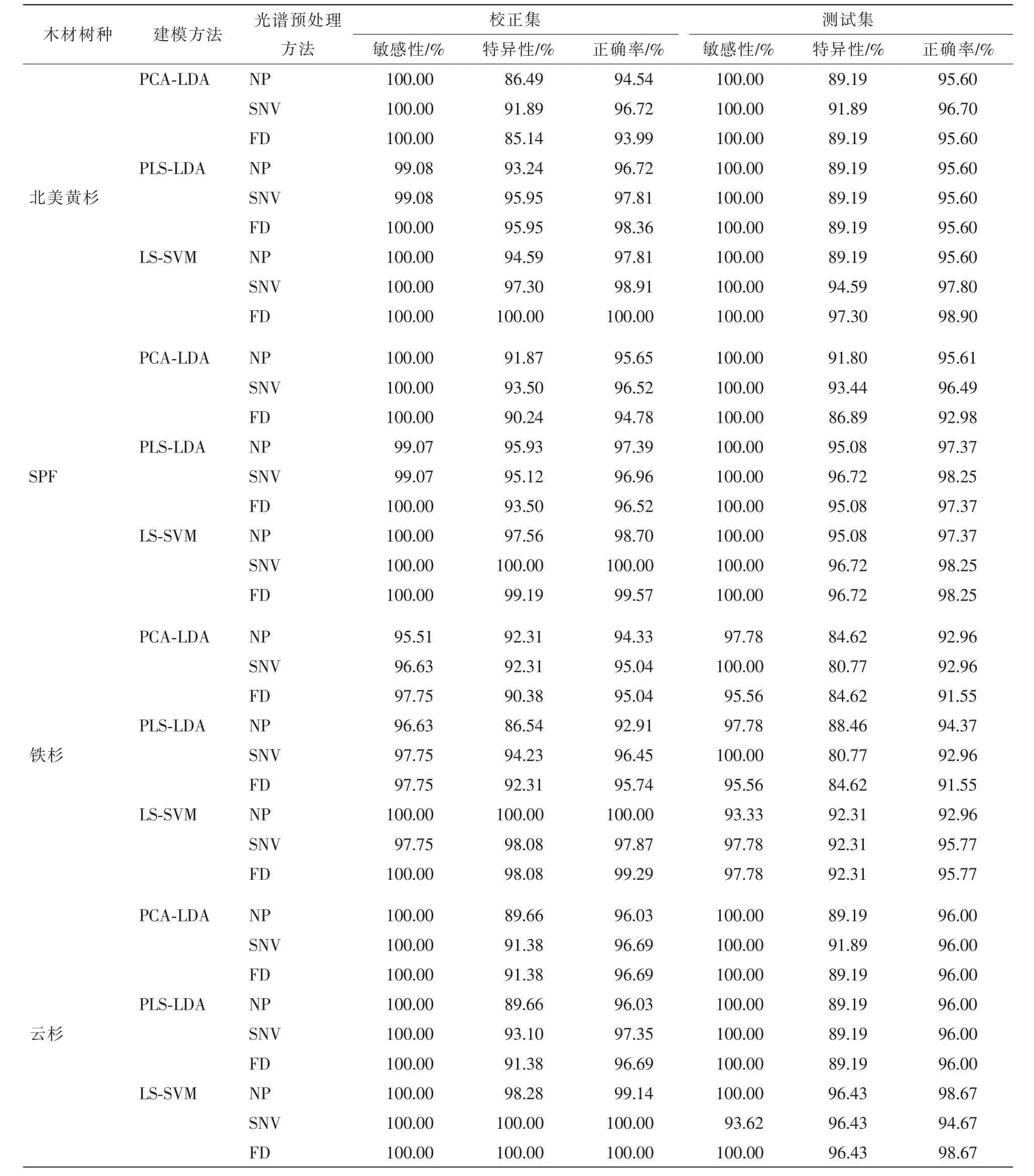
表2 不同光譜預處理下PLS-LDA和LS-SVM模型結果Table 2 PLS-LDA and LS-SVM results for different pre-processing methods

由圖1可知：盡管樹種不同，但它們的近紅外光譜具有一定的相似性，建立此4個樹種板材的混合節子識別模型可能具有更強的實際作用。采用LS-SVM建立混合節子識別模型，其結果如表4所示。

由表4可知：與單一樹種最優模型所用光譜預處理方法相同，采用一階導數預處理結合最小二乘支持向量機所建混合模型的性能最優。FD-LS-SVM模型對測試集的敏感性、特異性和識別準確率分別為99.50%，95.39%，97.72%。對比表3，該混合模型對SPF、鐵杉和云杉板材的預測結果與單一模型的預測結果一致，混合模型僅對北美黃杉板材的特異性（94.59%）略低于北美黃杉單一模型的同類指標（97.30%）。這表明混合樹種板材節子識別模型的適應性較強，更能適用于不同樹種板材的節子缺陷檢測。

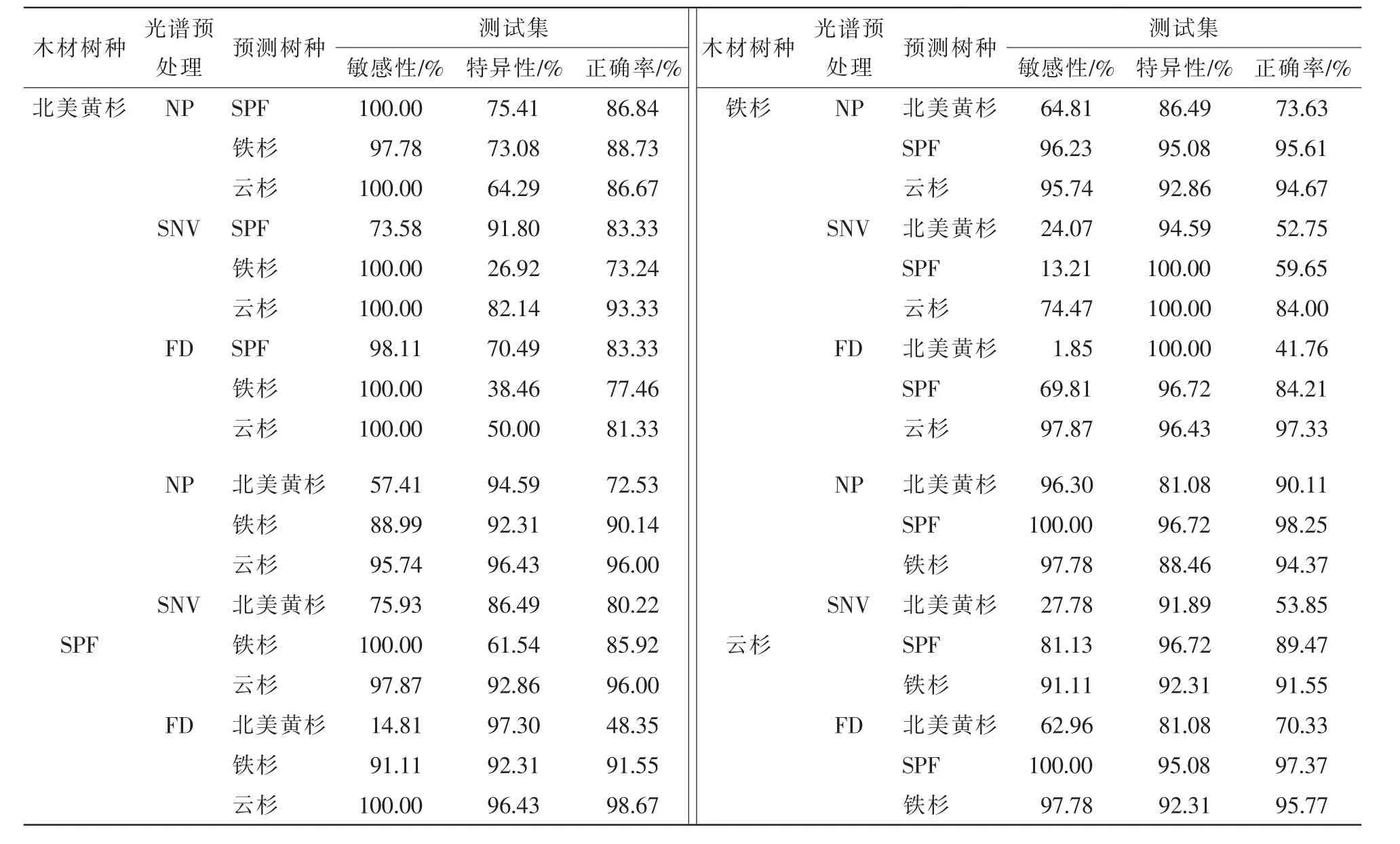
表3 單一樹種LS-SVM模型對其他樹種預測結果Table 3 Results of using a model built within one species to discriminate samples from other species

2.4 表面節子缺陷簡化模型的建立與分析

采用隨機青蛙算法（RF）對原始光譜的650個光譜變量進行特征變量選擇。將所有波長變量依RF算法運行100次后的平均被選概率進行排序，以0.72為閾值，選擇出概率最大的前8個變量作為特征波長，其結果分別為1 314，1 358，1 409，1 340，1 260，1 586，1 288和1 402 nm。其中，1 358 nm附近為木材中木質素，半纖維素和纖維素的C—H伸縮振動和變形振動的一級倍頻帶，1 409 nm附近為木質素及抽提物中C—H伸縮振動的一級倍頻帶，1 586 nm附近為木材纖維素中O—H伸縮振動的一級倍頻帶［24］。當木材表面存在節子缺陷時，其節子部位的主要化學成分如木質素、纖維素等的含量與正常部位存在差異［13］。因此，所選特征波長可以準確反映板材表面節子缺陷的化學特性。除此之外，板材的光譜數據矩陣從1 056×650降為1 056×8，可大大提高計算速度。

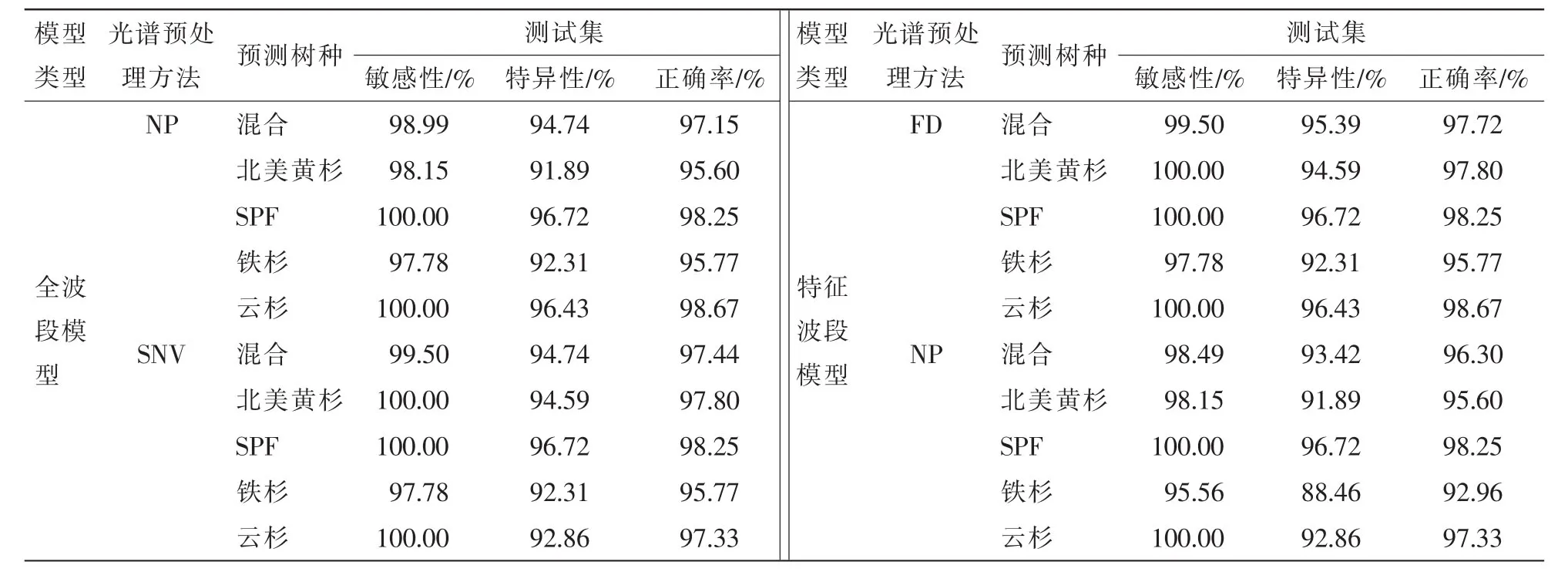
表4 全波段與特征波段下混合樹種板材LS-SVM模型結果Table 4 Results for full wavelengths models and effective wavelengths model

將8個特征波長（effective wavelengths,EWs）下的光譜數據作為輸入，采用LS-SVM建立混合板材表面節子缺陷特征波段識別模型（EWs-LS-SVM），并與原始光譜下全波段（full wavelengths,FWs）混合模型（FWs-LS-SVM）對比。結果如表4所示。

從表4中可以看出：EWs-LS-SVM模型測試集的敏感性、特異性和識別準確率分別為98.49%，93.42%，96.30%。與原始光譜下的FWs-LS-SVM模型相比，EWs-LS-SVM模型對測試集的特異性減小，表明EWs-LS-SVM模型對表面節子缺陷識別能力略有降低，這可能是由于EWs-LS-SVM模型只用了8個波長變量，從而導致有利于節子缺陷識別的部分信息丟失引起的。同時，對4個樹種板材進行具體分析發現：EWs-LS-SVM對測試集中北美黃杉和SPF板材的預測結果與FWs-LS-SVM模型結果相同，僅僅是鐵杉和云杉的預測結果有所降低。考慮到EWs-LS-SVM模型所用變量僅為FWs-LS-SVM模型的1.23%，該結果可以接受。

3 結論

采用近紅外光譜技術結合化學計量學方法研究了北美黃杉，SPF，鐵杉和云杉等4種針葉林板材表面節子缺陷的快速檢測方法。結果表明：一階導數光譜預處理結合最小二乘-支持向量機所建單一樹種板材節子識別模型以及混合樹種板材節子識別模型的性能最優；SPF，鐵杉和云杉板材中任一單一樹種板材的節子識別模型對其余2個樹種板材中的節子缺陷識別準確率較高，模型適應性較好，但北美黃杉板材節子識別模型不能用于其他3個樹種板材節子缺陷的識別，該模型適應性較差；采用隨機青蛙算法確定了8個特征波長變量（1 314，1 358，1 409，1 340，1 260，1 586，1 288和1 402 nm），能準確反映木材節子部位與非節子部位主要成分含量的差異；基于特征波長并采用最小二乘-支持向量建立的節子缺陷簡化模型性能較好，該模型對混合樹種板材測試集的敏感性、特異性和識別準確率分別為98.49%，93.42%，96.30%，雖然測試結果略低于全波段檢測模型，但考慮到所用波長變量僅占全波段變量的1.23%，所選特征波長可用于搭建板材節子缺陷檢測的快速分析系統。

［1］ 宋小燕，白福忠，武建新，等.應用灰度直方圖特征識別木材表面節子缺陷［J］.激光與光電子學進展，2015，52（3）：199-204.

SONG Xiaoyan,BAI Fuzhong,WU Jianxin,et al.Wood knot defects recognition with gray-scale histogram features［J］.Laser Optoelectron Prog,2015,52（3）：199-204.

［2］ KARSULOVIC J T,LEóN L A,GAETE L.Ultrasonic detection of knots and annual ring orientation in Pinus radiata lumber［J］.Wood Fiber Sci,2007,32（3）：278-286.

［3］ MACHADO J S,SARDINHA R A,CRUZ H P.Feasibility of automatic detection of knots in maritime pine timber by acousto-ultrasonic scanning［J］.Wood Sci Technol,2004,38（4）：277-284.

［4］ BARADIT E,AEDO R,CORREA J.Knots detection in wood using microwaves［J］.Wood Sci Technol,2006,40（2）：118-123.

［5］ CRISTHIAN A C,SANCHEZ R,BARADIT E.Detection of knots using x-ray tomographies and deformable contours with simulated annealing［J］.Wood Res,2008,53（2）：57-66.

［6］ LONGUETAUD F,MOTHE F,KERAUTRET B,et al.Automatic knot detection and measurements from X-ray CT images of wood：a review and validation of an improved algorithm on softwood samples［J］.Comput Electron Agric, 2012,85（5）：77-89.

［7］ CHEN Lijun,WANG Keqi,XIE Yonghua,et al.The segmentation of timber defects based on color and the mathematical morphology［J］.Optik-Int J Light Elect Opt,2014,125（3）：965-967.

［8］ XIE Yonghua,WANG Jingcong.Study on the identification of the wood surface defects based on texture features［J］. Optik-Int J Light Electr Opt,2015,126（19）：2231-2235.

［9］ POKE F S,RAYMOND C A.Predicting extractives,lignin,and cellulose contents using near infrared spectroscopy onsolid wood in Eucalyptus globules［J］.J Wood Chem Technol,2006,26（2）：187-199.

［10］ ANDRé N,LABBé N,RIALS T G,et al.Assessment of wood load condition by near infrared （NIR）spectroscopy［J］.J Mater Sci,2006,41（7）：1879-1886.

［11］ COGDILL R P,SCHIMLECK L R,JONES P D,et al.Estimation of the physical wood properties of Pinus taeda L. radial strips using least squares support vector machines［J］.J Near Infrared Spectrosc,2004,12（4）：263-270.

［12］ 楊忠，黃安民，江澤慧.近紅外光譜結合回歸分析預測法判別木材的生物腐朽［J］.林業科學，2012，48（10）：120-124.

YANG Zhong,HUANG Anmin,JIANG Zehui.Discrimination of wood biological decay by NIR coupled with regression analysis prediction method［J］.Sci Silv Sin,2012,48（10）：120-124.

［13］ FUJIMOTO T,TSUCHIKAWA S.Identification of dead and sound knots by near infrared spectroscopy［J］.J Near Infrared Spectrosc,2010,18（6）：473-479.

［14］ YANG Zhong,ZHANG Maomao,CHEN Ling,et al.Non-contact detection of surface quality of knot defects on eucalypt veneers by near infrared spectroscopy coupled with soft independent modeling of class analogy［J］.BioResources,2015,10（2）：3314-3325.

［15］ 楊忠，陳玲，付躍進，等.近紅外光譜結合SIMCA模式識別法檢測木材表面節子［J］.東北林業大學學報，2012，40（8）：70-72.

YANG Zhong,CHEN Ling,FU Yuejin,et al.Rapid detection of knot defect in wood surface by near infrared spectroscopy coupled with SIMCA pattern recognition［J］.J Northeast For Univ,2012,40（8）：70-72.

［16］ KENNARD R W,STONE L A.Computer aided design of experiments［J］.Technometrics,1969,11（1）：137-148.

［17］ 褚小立，袁洪福，陸婉珍.近紅外分析中光譜預處理及波長選擇方法進展與應用［J］.化學進展，2004，16（4）：528-542.

CHU Xiaoli,YUAN Hongfu,LU Wanzhen.Progress and application of spectral data pretreatment and wavelength selection methods in NIR analytical technique［J］.Prog Chem,2004,16（4）：528-542.

［18］ 鄭劍，周竹，仲山民，等.基于近紅外光譜與隨機青蛙算法的褐變板栗識別［J］.浙江農林大學學報，2016，33（2）：322-329.

ZHENG Jian,ZHOU Zhu,ZHONG Shanmin,et al.Chestnut browning detected with near-infrared spectroscopy and a random-frog algorithm［J］.J Zhejiang A&F Univ,2016,33（2）：322-329.

［19］ 鄭劍，周竹，仲山民，等.基于近紅外光譜的褐變板栗識別建模方法研究［J］.食品科技，2016，41（1）：285 -290.

ZHENG Jian,ZHOU Zhu,ZHONG Shanmin,et al.Detection of chestnut browning using different calibration methods based on near-infrared spectroscopy［J］.Food Sci Technol,2016,41（1）：285-290.

［20］ SUYKENS J A K,de BRABANTER J,LUKAS L,et al.Weighted least squares support vector machines：robustness and sparse approximation［J］.Neurocomputing,2002,48（1）：85-105.

［21］ LI Hongdong,XU Qingsong,LIANG Yizeng,et al.Random frog：an efficient reversible jump Markov Chain Monte Carlo-like approach for variable selection with applications to gene selection and disease classification［J］.Anal Chim Acta,2012,740：20-26.

［22］ 李洪東.廣義灰色分析體系建模的基本問題及其模型集群分析研究［D］.長沙：中南大學，2012.

LI Hongdong.Fundamental Problems of Generalized Grey Analytical Systems and Their Research of Model Population Analysis［D］.Changsha：Central South University,2012.

［23］ ALVES A,SANTOS A,ROZENBERG P,et al.A common near infrared-based partial least squares regression model for the prediction of wood density of Pinus pinaster and Larix×eurolepis［J］.Wood Sci Technol,2012,46（1）：157 -175.

［24］ SCHWANNINGER M,RODRIGUES J C,FACKLER K.A review of band assignments in near infrared spectra of wood and wood components［J］.J Near Infrared Spectrosc,2011,19（5）：287-308.

Knot detection on coniferous wood surfaces based on near infrared spectroscopy

ZHOU Zhu1,2,3,YIN Jianxin1,2,3,ZHOU Suyin1,2,3,ZHOU Houkui1,2,3
（1.School of Information Engineering,Zhejiang A&F University,Lin’an 311300,Zhejiang,China;2.Zhejiang Provincial Key Laboratory of Forestry Intelligent Monitoring and Information Technology,Zhejiang A&F University, Lin’an 311300,Zhejiang,China;3.Research Center for Smart Agriculture and Forestry,Zhejiang A&F University, Lin’an 311300,Zhejiang,China）

To develop a calibration model for rapid,accurate,and nondestructive grading of wood on the basis of knots,near infrared spectroscopy（NIRS）technology was used on coniferous boards from Douglas fir（Pseudotsuga menziesii）,Chinese hemlock （Tsuga chinensis）,Dragon spruce （Picea asperata）,and Spruce（Picea glauca and Picea engelmannii）-Pine（Pinus contorta）-Fir（Abies lasiocarpa）（SPF）.Altogether 1 056 spectrums of samples were obtained in the wavelength range of 1 000-1 650 nm by SmartEye1700.Spectral pretreatment methods,including standard normal variate （SNV）and first derivative （FD）as well as modelling methods such as principal component analysis-linear discriminant analysis （PCA-LDA）,partial least squareslinear discriminant analysis （PLS-LDA）,and least squares-support vector machine （LS-SVM）were used and compared.The experiments also explored the ability of using a model built for one species to predict samples from other species.Then,a random frog algorithm was applied to select effective wavelengths（EWs）.Finally,aLS-SVM model was established to detect knot defect on board surfaces based on eight effective wavelengths（EWs）or only 1.23%of the full wavelengths with results compared based on sensitivity,specificity,and accuracy.Results of the validation set of mixed boards were：sensitivity--98.49%,specificity--93.42%,and accuracy--96.30%.Thus,near infrared spectroscopy combined with chemometric methods could be used to detect surface knots on boards for different species of wood with the random frog algorithm being a powerful tool for selecting efficient variables to optimize the model and improve detection efficiency.［Ch,2 fig.4 tab.24 ref.］

wood science and technology;near infrared spectroscopy;coniferous wood;board;knot;random frog algorithm;least squares-support vector machines（LS-SVM）

S781.5;O657.3

A

2095-0756（2017）03-0520-08

浙 江 農 林 大 學 學 報，2017，34（3）：520-527

Journal of Zhejiang A＆F University

10.11833/j.issn.2095-0756.2017.03.018

2016-06-14；

2016-11-18

浙江省自然科學基金資助項目（LQ13F050006，LY15C140005）；浙江農林大學智慧農林業中心預研項目（2013ZHNL03）；浙江農林大學科研發展基金資助項目（2012FR085）

周竹，講師，博士，從事木材智能化檢測技術等研究。 E-mail：zhouzhu@zafu.edu.cn