基于點云數據的數字化比對檢測系統設計與實現

陳芷+吳捷+馬小虎

摘 要： 點云數據與CAD模型的坐標匹配和對應關系的建立是數字化比對檢測系統的關鍵技術。利用k?D樹空間快速搜索策略改進傳統ICP算法實現點云數據與CAD模型坐標精確匹配，采用半邊數據結構建立點云數據與CAD模型對應關系，利用點到邊和點到點的對應關系解決待測工件的邊緣和棱線以及特征明顯變化區域的偏差檢測問題。在此基礎上研制了數字化比對檢測系統。試驗結果表明該系統運算速度快、精度高，具有很好的應用效果。

關鍵詞： 坐標匹配； 點云數據； 對應關系建立； 對比檢測

中圖分類號： TN911.23?34； TP391.7 文獻標識碼： A 文章編號： 1004?373X（2017）12?0162?03

Abstract： The coordinate matching between point cloud data and CAD model and establishment of their corresponding relation are the key technologies of digital contrast detection system. The k?D tree space fast search strategy is used to improve the traditional ICP algorithm to achieve the coordinate accurate match between point cloud data and CAD model. The half edge data structure is adopted to build the corresponding relation between point cloud data and CAD model. The corresponding relation of point?to?edge and point?to?point is employed to solve the deviation detection problem of edge and ridge of UUT， and the region with obvious feature variation. On the above basis， a digital contrast detection system was developed. The test results indicate that the system has fast calculating speed and high precision and good application effect.

Keywords： coordinate matching； point cloud data； corresponding relation establishment； contrast detection

隨著制造業的發展，自由曲面等復雜型面已廣泛地應用于產品的設計和制造過程中。為了保證具有復雜型面工件的加工質量以及生產效率，需要對其進行快速精確的誤差檢測。而傳統模板檢測方法由于自身諸多不足已不能滿足實際生產要求[1]。數字化比對檢測技術的出現為解決這一難題提供了新的途徑[2]。目前在國外，許多著名的汽車制造廠商比如豐田、大眾、通用等均已將數字化比對檢測技術逐漸應用于實際生產過程中，大大降低了產品開發制造成本，縮短了產品開發制造周期[3]。而在國內，數字化比對檢測技術的應用幾乎還是空白，數字化比對檢測技術尚未成熟，其中主要的關鍵技術有待進一步的研究。因此，必須要對這些關鍵技術進行深入研究，讓數字化比對技術能夠真正地應用于實際，滿足生產要求。

1 坐標匹配

坐標匹配就是要計算得到點云數據與CAD模型之間的坐標變換矩陣，通過矩陣運算，使得點云數據與CAD模型處于同一個坐標空間下[4]。

1.1 ICP算法

ICP（Iterative Closest Points）算法通過搜索點云數據與CAD模型中的最近點點對，并利用這些最近點對間的距離構造目標函數，進行迭代運算最終求出坐標旋轉、平移矩陣，使得目標函數值最小[5]。通常原始ICP算法空間搜索的時間復雜度是，其中和表示點云數據和CAD模型頂點集中點的數目。如果點的數量很大，這個過程將非常耗時，因此最近點點對的搜索是ICP算法的瓶頸。本文利用k?D樹來進行最近點對的搜索，大大提高了搜索效率。

1.2 k?D樹空間搜索策略

k?D樹是一個針對K維度空間所設計的二元搜索樹，其本質是一個二叉樹[6]，其典型應用是求點的k個最近點。k?D樹的生成過程就是平面被軸和軸連續遞歸劃分的過程，直到最后分割的區域內只有一個點。這樣的分割過程就對應了一個完全二叉樹，二叉樹的分支節點對應一條分割線，而每個葉子節點就對應一個數據點。利用k?D樹進行最近點對搜索的時間復雜度為，遠小于傳統的遍歷算法。因此，運用k?D樹空間搜索策略可以在很大程度上提高ICP算法的計算效率。

2 對應關系

通常對于點云數據與CAD模型對應關系的建立主要是尋找各點所對應的CAD模型上的面片，利用點云各點與CAD模型面片之間的距離表示偏差[7]，然而這些方法不能保證在所有區域都能得到正確的計算結果。通過建立半邊數據結構表達CAD模型表面三角形面、邊、頂點的拓撲關系，增加點到邊的對應關系和點到點的對應關系，可以彌補傳統方法的不足。

2.1 半邊數據結構

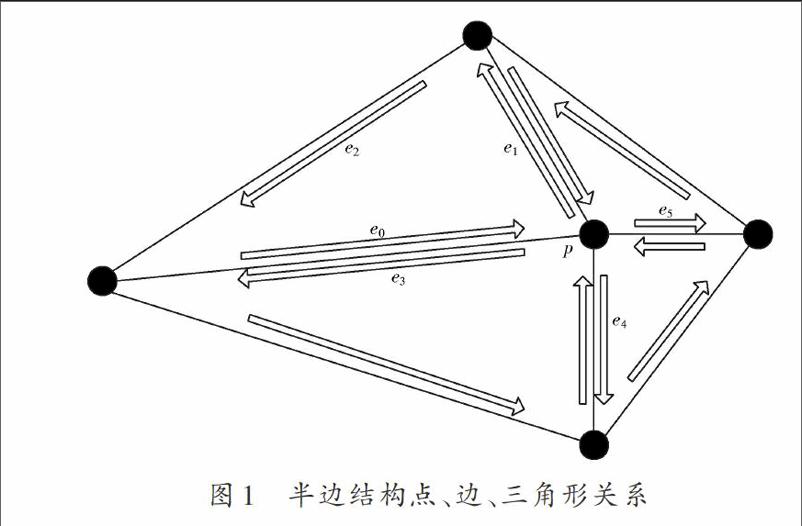
半邊數據結構是一種以界限為基礎的拓撲結構。其基本原理是把三角網格的每條連線分為兩個相等且方向相反的半邊（邊界除外）[8]，如圖1所示。圖1中有四條邊以點為起點，分別為：，，和。索引信息分別儲存在點的結構里，通過找到點，就可以遍歷其所連接邊的鄰邊、孿邊快速得到鄰近三角形的所有信息。

2.2 點對面的關系

建立點對面的對應關系是點云數據比對檢測的基礎。首先對于CAD模型中所有頂點的坐標信息建立k?D樹數據結構，快速搜索點云中各點所對應的CAD模型上的最近頂點。然后通過半邊結構從該對應點開始遍歷與該點相連的所有三角面片，根據判斷準則找出符合要求的三角面片。

2.3 點對邊的關系

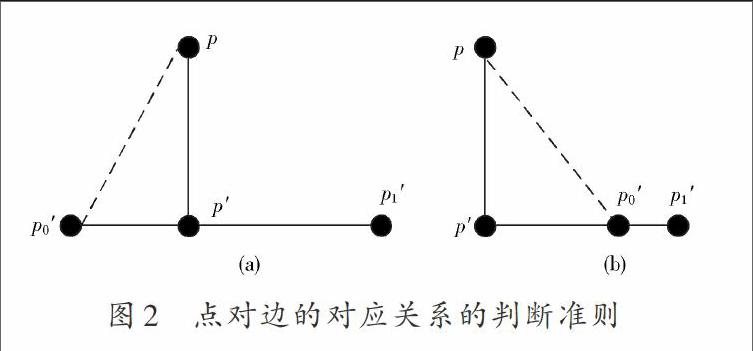
由于在待測工件的邊緣和棱線以及特征明顯變化的區域附近，點云數據中的點很難在CAD模型上找到滿足要求的對應三角面片。如果在這些地方依然采用點對面的對應關系來進行處理顯然是行不通的，必須尋找出滿足條件的對應邊來建立對應關系。其對應邊判斷準則如圖2所示。

首先，計算出點數據中點對于CAD模型中邊的投影點坐標；其次，通過計算投影點到邊的兩個端點的距離之和是否大于該邊的長度判斷投影點是否在邊上，若大于則說明投影點不在邊上。根據這個判斷條件，圖2（a）滿足條件，則可以確定該邊是點的對應邊，而圖2（b）則不滿足該判斷條件，則認為點與該邊沒有對應關系。

2.4 點對點的關系

如果經過上述兩個步驟，點云上的點依然沒能夠建立點對面或者點對邊的對應關系的話，那么將此點與其在CAD模型中的最近點組成點對點的對應關系，以這兩個點的距離來表示偏差。這種情況一般會出現在待測工件中的棱角和具有尖銳特征的地方。

3 系統實現

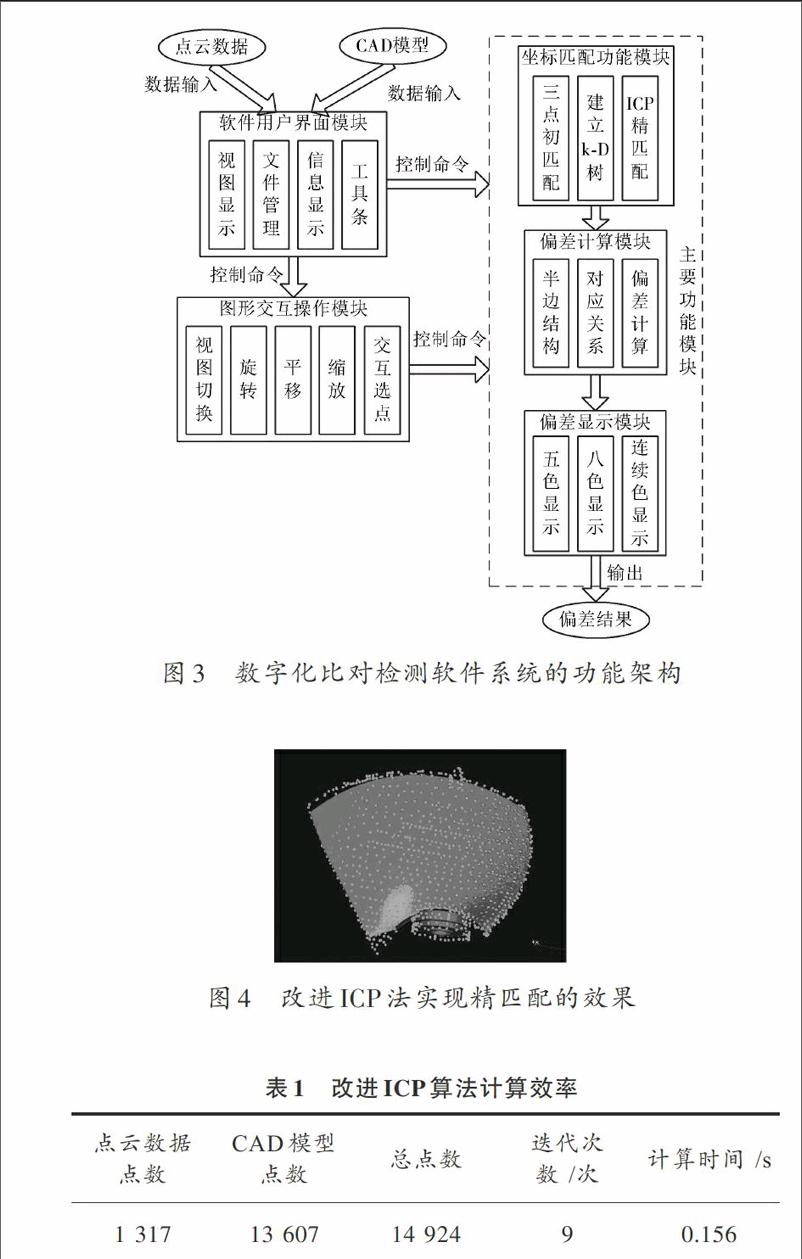
檢測系統主要功能包括：點云數據與CAD模型初步坐標匹配、坐標精匹配、點云數據各點偏差計算以及色斑圖顯示偏差結果等功能模塊。圖3表明了本文所開發的整個數字化比對檢測系統各個功能模塊的關系。

4 試驗分析

4.1 處理效率

對于改進ICP法的計算效率主要取決于收斂速度，即進行多少次的迭代運算。下面通過某水輪機葉片的點云數據與其CAD模型來對該系統的ICP坐標匹配模塊進行分析。利用改進ICP法進行坐標精匹配時，選擇最近點對距離的平均值作為目標函數，并設置ICP法的收斂條件為兩次迭代運算的目標函數值相差的絕對值小于作為收斂判斷條件，經過了9次迭代運算之后最終滿足收斂條件，完成匹配，效果如圖4所示。

根據測量，最終得到的改進ICP法的計算效率如表1所示。從上述試驗檢測結果來看，改進ICP算法實現點云數據與CAD模型坐標精匹配計算效率較快，能夠滿足實際使用需求。

4.2 偏差精度

本系統采用與德國GOM公司開發的TRITOP系統中的點云數據檢測模塊進行偏差計算結果比較分析來側面地反映系統的精度。兩個點云檢測模塊對葉片的檢測結果如圖5所示。可以看到兩者的處理結果在大體上是一致的。

然而由于TRITOP軟件的檢測原理是指用計算點云數據各點對CAD模型面片的最近距離來表示偏差，因此在邊緣棱角或者特征顯著變化的區域，其計算結果是不準確的，如圖6（a）所示，當偏差計算范圍是時發現TRITOP系統對于左側邊緣的部分點云數據由于與CAD模型上錯誤的面片建立了對應關系，導致偏差計算的失效。而本系統由于在邊緣等特定區域采取了建立點對邊和點對點的對應關系，很好地解決了這些特殊區域偏差的檢測問題，取得了很好的效果。如圖6（b）所示，在相同的偏差計算范圍下，可以看到在TRITOP系統中處理錯誤的點都得到了正確的偏差計算結果。

5 結 語

本文利用k?D樹空間快速搜索策略改進ICP算法，采用半邊結構來表達單元三角網格形式CAD模型的點、邊、面拓撲結構，以滿足在建立點云數據與CAD模型對應關系時要快速遍歷CAD模型中所有幾何元素的要求，并在此基礎上研制了數字化比對檢測系統。通過對某水輪機葉片檢測，結果表明該系統運行效率快、精度高，具有很好的應用效果。

參考文獻

[1] 高中亞，李振平，方海濱，等.二維復雜型面數字化比較技術的應用[J].工具技術，2015，49（5）：60?62.

[2] 陸峰，李寧，趙德宏.復雜曲面三維輪廓精度數字化比對檢測與誤差分析[J].制造業自動化，2014（18）：46?50.

[3] 陳勝利.快速成形技術及其發展趨勢[J].制造業自動化，2009，31（10）：24?26.

[4] MA Hongchao， SUN Jie. Intelligent optimization of seam?line finding for orthophoto mosaicking with LiDAR point clouds [J]. Journal of Zhejiang University： Science C， 2011， 12（5）： 417?429.

[5] LI Jianchuan， YU Jianfeng. A new posture evaluation method of wing based on iterative closest point algorithm [J]. Advanced materials research， 2013， 718/720： 1279?1285.

[6] 魏海濤，杜云艷，任浩瑋，等.基于N?KD樹的空間點數據分組算法[J].地球信息科學學報，2015（1）：1?7.

[7] 徐偉恒，馮仲科，蘇志芳，等.一種基于三維激光點云數據的單木樹冠投影面積和樹冠體積自動提取算法[J].光譜學與光譜分析，2014（2）：465?471.

[8] 王繼東，陳桂林.基于半邊數據結構的最短路徑算法及其實現[J].計算機工程與應用，2009（8）：118?120.