承壓舟浮橋結構強度直接計算研究

鄭培培 裴志勇 劉維勤 趙慶亮

(武漢理工大學交通學院1) 武漢 430063) (武漢理工大學高性能艦船技術教育部重點實驗室2) 武漢 430063)(山東省濟南船舶檢驗局3) 濟南 250014)

承壓舟浮橋結構強度直接計算研究

鄭培培1)裴志勇1,2)劉維勤1,2)趙慶亮3)

(武漢理工大學交通學院1)武漢 430063) (武漢理工大學高性能艦船技術教育部重點實驗室2)武漢 430063)(山東省濟南船舶檢驗局3)濟南 250014)

承壓舟浮橋以其建造成本低、周期短、經濟性好、通行能力強等優點在不通航水域獲得了較為廣泛的應用，目前為止尚沒有專門的技術規范可用.對承壓舟浮橋結構強度直接計算進行了研究，根據其結構形式和受力特點，考慮其所承受的極端載況，定義了5種典型計算工況.對橫艙壁設置、連接橋底封板對結構強度的影響進行了討論，還對該承壓舟浮橋進行了典型載況的動應力測試，將測試結果與計算結果進行了比較分析，驗證了計算工況的合理性和計算過程的可靠性.

承壓舟浮橋；計算工況；結構強度；強度衡準；動應力測試

0 引 言

承壓舟浮橋是我國首創的一種舟型，在黃河流域這類不通航水域獲得了較為廣泛的應用[1].其建造成本低，建造周期短，經濟性好，而且通行能力大，近些年設計建造的承壓舟浮橋允許通行的車輛載重量大多超過100 t，最大達到180 t，為兩岸經濟的發展做出了重大貢獻.黃河中下游蕩型河道地勢復雜，易形成淺灘，在這種情況下其他類型浮橋很難架設，而承壓舟浮橋能很好適應這種狀況，它既能在漂浮狀態又能在落灘及半落灘狀態下使用.隨著社會重載車輛通行需求的逐漸增加，承壓舟浮橋通行能力和安全保障能力也迫切需要提高，然而目前沒有相對完善的技術規范和檢驗法規，制約著其進一步發展[2].浮橋的安全性是浮橋搭建、運營的前提，其結構強度校核評估又是安全性的關鍵.目前有關承壓舟浮橋的研究以研究車輛移動載荷的動態響應居多，對其結構強度全面系統的研究較少[3-6].姜玥等[7]對承壓舟浮橋的屈服強度進行了評估，并對其進行了疲勞損傷和疲勞壽命計算.但他們研究的浮橋為單向通行的浮橋，且通行的車輛載重量較小，不適宜于現有承壓舟浮橋強度評估.王楠等[8]對高寒地區浮橋結構進行了結構-熱耦合分析，探討了一種冰高寒地區浮橋強度校核法，側重于研究網格尺寸、載荷加載方式及計算動載荷下浮橋動態放大系數.

文中對山東省第四代承壓舟浮橋結構強度直接計算進行了研究，結合實際使用情況，定義了5種典型工況，進行結構強度衡準，并對該承壓舟浮橋進行了典型工況下結構動應力測試[9]，以驗證所選取計算工況的合理性和計算方法的可靠性.

1 承壓舟浮橋發展

承壓舟浮橋由多艘承壓舟通過支耳鉸接而成，承壓舟為短而寬的雙體船，車道沿船寬方向布置.目前承壓舟浮橋的發展已歷經30余年，有三代成熟舟型.第一代舟型于1987年研制成功，適合輪式15 t、履帶式40 t車輛單向通行，儲備浮力很小(型深1.3 m，設計吃水1.0 m)，首尾為方形.第二代舟型于1995年開始設計研發，承載浮力均不超過100 t，基本在40～90 t，可滿足整車質量20 t以下車輛的雙向通行；舟型采用尖首以利于分水，船長多不超過20 m、寬不超過18 m，設計吃水均為1.0 m，型深多為1.5 m，儲備浮力有了較大提升，部分舟型專設了人行道以實現人車分流.第三代舟型的儲備浮力大大提高，可允許100 t以上重載車輛單向通行，整車質量低于50 t的車輛可雙向通行；結構強度較之前舟型有較大提高，局部設計有了改進，安全性能有了較大提升.第一代和第二代承壓舟由于通行車輛重量較小，并未考慮V形坡的影響，第三代承壓舟通行車輛重量超過100 t后，船體鉸接處易形成V形坡，為最大限度避免V形坡的不利影響，第三代舟型船寬大多不低于20 m.近年來隨著黃河兩岸經濟的快速發展，重載掛車通行需求越來越多，單向通行導致“壓車”非常嚴重，有時排隊2～3 km，通行時間超過1 h，與社會需求嚴重不符.研發的第四代舟型，船長和船寬均超過30 m，儲備浮力大大提高，設計為雙向四車道通行，中間車道可允許整車質量不超過147 t的載重掛車雙向通過.承壓舟浮橋會承受橫向彎矩、橫向轉矩和彎扭組合作用，尤其是落灘片體受力狀況惡劣，但是目前承壓舟在設計研發上尚無可供遵循的規范，因此需要通過結構強度直接計算的方法對其進行強度衡準.

2 結構強度直接計算

2.1 研究對象

文中研究對象是山東省胡家岸1 000 t級雙向四車道承壓舟浮橋，為研制的第四代承壓舟浮橋.設有四條行駛車道，車道沿船寬方向分布，車道總寬度19 m，約占總長48%.中間兩條車道均寬5.5 m，供重載車輛行駛，兩條邊車道均寬4 m，供小車行駛.該承壓舟浮橋由12艘雙體承壓舟鉸接而成，承壓舟為雙體船，每個片體單甲板，單舷側，承壓舟主尺度見表1.主車道甲板按舟橋設計，除船底中部為縱骨架式外，其余均為橫骨架式.車道下方橫向構件的間距設計時要保證重載掛車一側雙排車輪作用在不同板格上，單個重載車輪著地寬度為0.2～0.3 m，車道下方強框架間距為1 m，強框架之間設計有兩道普通構件以減小板格寬度至0.333 mm.

承壓舟浮橋由帶舷伸結構的雙體船鉸接而成，其結構強度計算大多是參考內河雙體船規范.但是承壓舟與常規雙體船相比有很大不同，當前船舶規范都是基于船體處于“浮態”的研究集成，計算考慮的外載荷主要是波浪載荷，而承壓舟由于工作環境的緣故，所受波浪載荷很小.此外，承壓舟工作時處于靜浮和落灘兩種狀態：承壓舟浮橋一端最靠近岸邊的片體落灘，另一端有兩個承壓舟落灘，其余大部分承壓舟浮在水中.靜浮狀態，船體主要承受車輛載荷和浮力；落灘狀態，船體主要承受車輛載荷和地基支持力.另外，承壓舟船體之間是通過支耳鉸接，多船體之間相互作用需要考慮.因此承壓舟浮橋結構強度需要通過結構強度直接計算的方法進行評估.

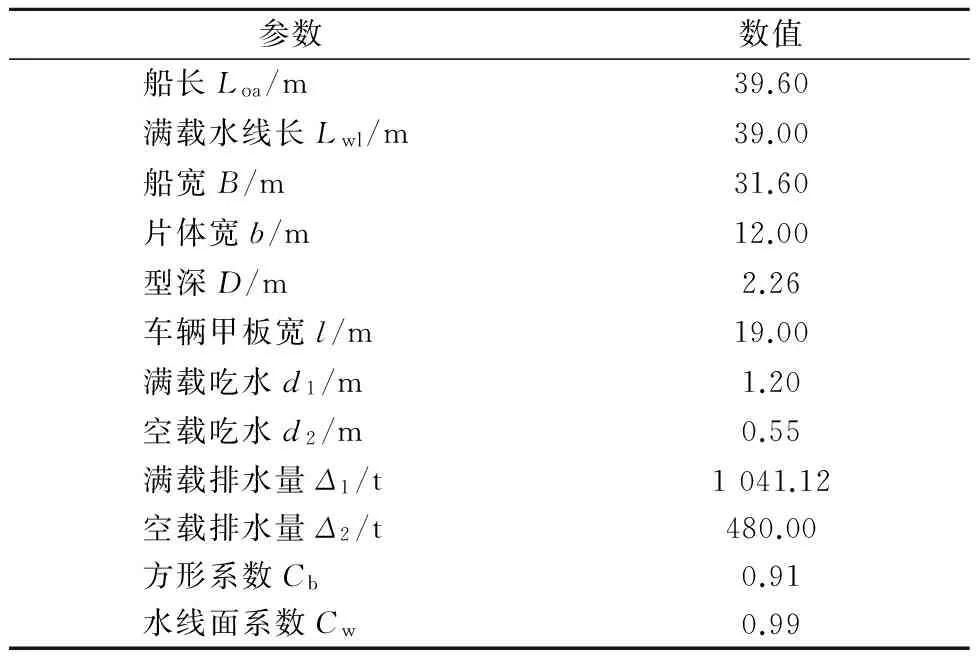
表1 承壓舟主尺度

2.2 計算模型

考慮到實際工作情況，浮橋是由多艘雙體船連接而成，單艘雙體船的計算狀態并不能很好的反映實際工作狀態，應考慮多艘雙體船連接而成的系統進行結構強度直接計算分析，所以建立了三船體有限元模型，有限元模型見圖1.各雙體船之間采用多點約束(multi point constraint，MPC)來模擬支耳的鉸接作用.耦合自由度除了放開繞船長方向的轉動外，其他方向自由度保持耦合，從而達到鉸接連接的作用.板殼和主要構件腹板用板單元模擬，主要構件面板和普通構件用梁單元模擬，一共115 108個節點，123 965個板單元，77 662個梁單元.單元尺寸上，沿船寬方向按縱骨間距劃分單元，網格大小為500 mm；沿船長方向按肋骨間距劃分單元，中部車輛通行區域網格大小為333.33 mm，其他區域網格大小為500 mm.強橫梁作為主要受力構件，沿其腹板高度方向劃分為6個單元，其他強構件沿腹板高度方向劃分為3個單元.

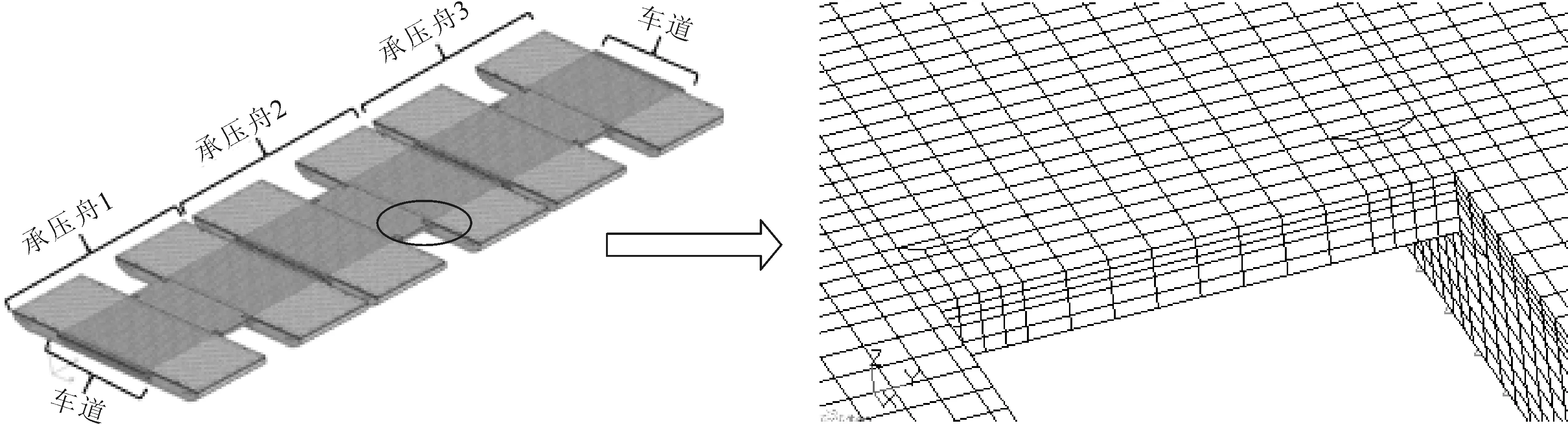
圖1 承壓舟浮橋三維有限元模型及連接橋局部放大圖

2.3 計算工況

承壓舟浮橋在使用時，主要承受甲板和連接橋上移動的車輛載荷及底部浮力作用(靜浮時)或支反力作用(落灘時).車輛通行方向是沿承壓舟寬度方向，車輛移動到不同位置時會導致承壓舟承受橫向彎矩、橫向轉矩及彎扭組合作用.尤其是連接橋較寬且為單層甲板，連接橋結構是船體結構強度最為薄弱部分.基于承壓舟浮橋受力特點，考慮連接橋承受極端橫彎、橫扭及彎扭組合作用，定義了5種典型工況，代表了承壓舟浮橋承受的最惡劣工況.

工況1，大車車輪和小車集中在承壓舟連接橋兩端的兩個片體上，評估連接橋橫彎和橫扭強度，工況1車輛位置示意圖見圖2.工況2，大車車輪和小車以中心對稱的方式集中在承壓舟兩個片體上，且大車后車輪作用在外伸舷處，評估連接橋橫扭強度.工況3，大車后車輪和小車集中在單個連接橋上，評估連接橋橫彎強度.工況4，大車重載車輪和小車集中在承壓舟一個片體上，且大車后車輪作用在外伸舷處，評估連接橋橫彎強度.工況5，承壓舟一個片體落灘，車輛載荷主要集中在與其相鄰的連接橋和另一個片體上，評估落灘片體的連接橋橫彎強度.

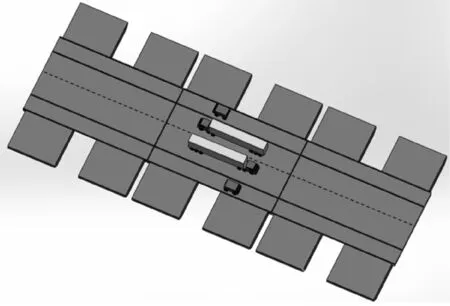
圖2 工況1車輛位置示意圖

參考現有通行車輛的軸重分布情況，中間兩個車道設計通行載重147 t的大載重掛車，外圍兩個車道設計通行10 t的小型農用貨車.147 t的大載重掛車參數見圖3.由于車輛載荷主要是通過車輪作用于甲板，作用面積相對甲板很小，計算時把車輛載荷考慮為節點力施加到甲板上，同時通過引入動載荷系數來考慮動載荷效應.車輛行駛時引起的浮力變化通過在船底施加線性彈簧單元來模擬.

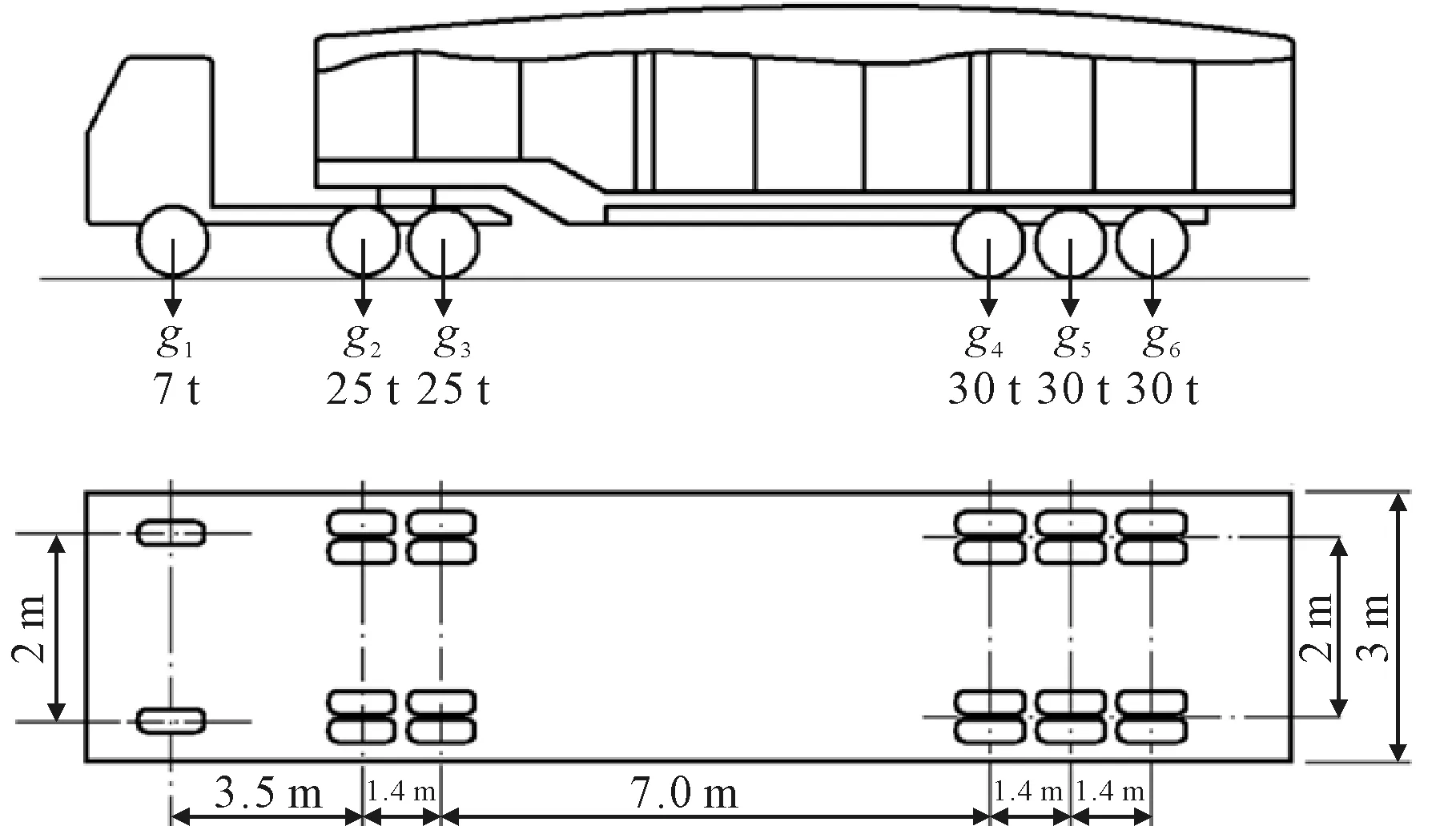
圖3 大載重掛車示意圖

2.4 計算結果及分析

工況1中，大車車輪和小車集中在承壓舟連接橋兩端的兩個片體上，此時連接橋承受彎扭組合作用，橫艙壁位于車道正下方, 上端與甲板強橫梁相連，橫艙壁上端靠近內舷側部位整體應力較大,最大應力為164 MPa.工況1計算結果見圖4.

圖4 工況1計算結果

工況2中，連接橋承受橫向轉矩，由于車道位于船體中部且承壓舟儲備浮力較大，車輛作用片體上時，引起的首尾吃水差較小，因此連接橋承受的轉矩相對較小，承壓舟整體應力較小，最大應力為98.6 MPa，最大應力位置位于中部橫艙壁上端靠近內舷側部位.

工況3中，車輛重載車輪均落在連接橋上，連接橋承受較大的橫向彎矩，連接橋上甲板強橫梁作為主要受力構件，整體應力較大，連接橋中部甲板強橫梁上最大應力達到153 MPa.

工況4中，車輛載荷大多作用在一個片體上，受車輛載荷作用的片體向下位移較大，受車輛載荷作用的片體和未受車輛載荷作用的片體之間產生位移差，連接橋承受彎矩作用，中部橫艙壁上端靠近內舷側部位整體應力較大，最大應力為164 MPa.

工況5中，承壓舟一個片體落灘，另一個片體浮在水中，車輛作用在靜浮的片體上，落灘片體位置固定，承受載荷片體產生較大的向下位移，連接橋與落灘片體交接處承受較大彎矩作用，此時連接橋上強橫梁與內舷板交接處應力較大.且承壓舟在使用過程中，由于落灘片體為不均勻落灘，連接橋承受轉矩作用，連接橋邊緣甲板強橫梁應力很大，最大應力為152 MPa.

承壓舟浮橋在營運時，連接橋會承受彎矩和轉矩作用，甲板強橫梁作為主要受力構件，整體應力較大.橫艙壁作為車道下方支撐結構，上端與甲板強橫梁相連，連接橋在承受彎矩或轉矩作用時，甲板強橫梁與片體交接部位應力較大，且會對橫艙壁形成擠壓，因此橫艙壁上端靠近內舷側部位應力較大.

3 結構布置優化

3.1 橫艙壁布置

承壓舟橫艙壁對保證船體的橫向強度和剛性起很大的作用，改變橫艙壁布置形式，研究橫艙壁的布置對結構強度的影響，找出合適的橫艙壁布置位置.將中間厚度為8 mm的橫艙壁改為兩塊橫艙壁，兩橫艙壁距離為一個強框架間距(1 m)，見圖5，另外改變橫艙壁的厚度分別為4，6和8 mm，探討橫艙壁厚度對結構強度的影響.

圖5 橫艙壁結構更改示意圖

當雙橫艙壁厚度均為6 mm時，承壓舟浮橋應力最小，計算結果見表2.單橫艙壁形式改成雙橫艙壁形式之后，當橫艙壁厚度為4 mm時，最大應力位置在橫艙壁上，隨著橫艙壁的厚度增加至6 mm，最大應力減小且最大應力位置轉移到連接橋甲板強橫梁上.隨著橫艙壁厚度繼續增加至8 mm時，連接橋甲板強橫梁上應力變大.橫艙壁可視為船底、舷側和甲板等結構的一個支座，參與船體各部位構件之間作用力的相互傳遞.雙橫艙壁厚度為4 mm時，橫艙壁整體結構較弱，與單艙壁厚度為8 mm時相比變形較大，因此最大應力位置在橫艙壁上，當橫艙壁厚度增加至6 mm時，橫艙壁整體結構變強，變形相對減小，最大應力位置轉移至甲板強橫梁上，隨著橫艙壁厚度繼續增加，橫艙壁整體變形越來越小，橫艙壁的應變能也越來越小，因此甲板強橫梁應力越來越大.

表2 不同橫艙壁布置形式計算結果

3.2 底封板布置

改變底封板的數目，研究底封板的布置對結構強度的影響.制定了四個方案：方案一不設置底封板，方案二設置4塊底封板，方案三設置6塊底封板，方案四設置10塊底封板.底封板為6 m×1 m×8 mm的鋼板，間隔著一個肋位布置在連接橋底部，四種方案的底封板由連接橋兩側逐漸向連接橋中部布置，底封板布置見圖6，方案四以間隔一個肋位的布置方式布滿連接橋.

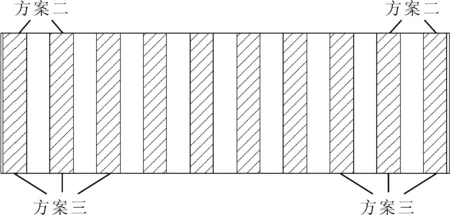
圖6 各方案底封板布置示意圖

四種方案均是車輛位置如工況1所示時承壓舟浮橋應力最大，且最大應力位置均在橫艙壁靠近內舷側部位，四種方案計算結果見表3.當底封板數目由0增加至6塊時，連接橋抗彎抗扭強度增加，中部橫艙壁應力因此減小，繼續增加底封板數目至10塊時，連接橋結構形式與無底封板時相比改變較大，連接橋上各部位結構均得到加強，此時承壓舟浮橋整體應力重新分布，橫艙壁結構較為薄弱，其應力急劇增大.

表3 四種方案計算結果

4 實橋測試

4.1 測試目的及方案

參考結構直接計算結果，在應力位置較大部位布置測點，測點布置在靠近岸邊的第七個靜浮片體上和一個最靠近岸邊的落灘片體上.靠近岸邊的第七個片體靜浮在水中，受彎矩和轉矩聯合作用時，連接橋應力水平較高；落灘的片體落灘狀態復雜，船底部分區域落灘，受力情況惡劣，連接橋與落灘片體交接處應力較大.測點布置一共78個通道，共計38個測點：其中靜浮片體上有54個通道，共計26個測點；落灘片體24個通道，共計12個測點.本次測試對胡家岸承壓舟浮橋首先進行了營運時各種載況的結構動應力測試，不同車輛的載重量不同且兩車道上車輛行駛狀況也不同，因此承壓舟受力狀況十分復雜，營運時會承受各種不同載荷工況.通行車輛較多時如通行車輛以車隊形式通過承壓舟時，前后車輛之間車距相對較小，且雙向車道車輛數都較多，此時測試片體中，不均勻落灘的片體會承受較大的轉矩和彎矩載荷作用，靜浮片體會承受彎矩和車輛重量引起的轉矩的作用；通行車輛較少時，前后車輛之間車距較大，且存在一側車道通行車輛比對象車道車輛多且重量要重得多的情況，承壓舟受力不均，此時轉矩較大，起主要作用.

落灘片體受力狀況較惡劣，選取應力水平較高的7處測點的測試結果與計算結果進行比較，測點布置見圖7.測得靠近Fr.21肋位一側車道180 t重載掛車通過，靠近Fr.40肋位一側車道120 t重載掛車通過時各測點應變，根據測試結果得到各測點最大應力值.

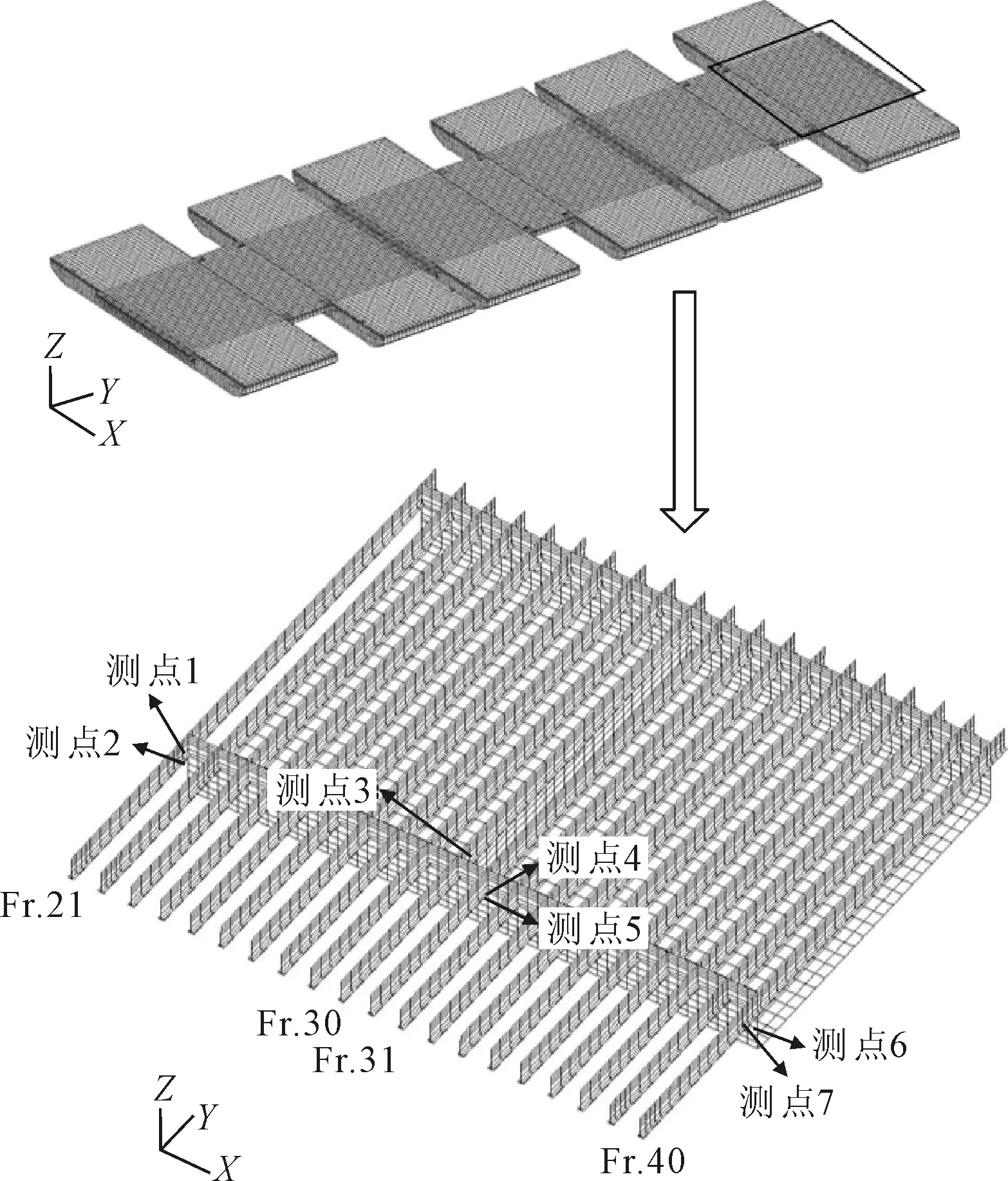
圖7 實橋測試時落灘片體測點布置示意圖

4.2 測試結果分析

測試結果表明，對于靜浮片體，除了欄桿應力較大之外，其他部位應力都較小.對于落灘片體，連接橋邊緣及中部強橫梁面板應力較大，且Fr.40肋位強橫梁面板應力遠大于Fr.21肋位強橫梁面板應力，這是由于落灘片體底部不均勻落灘，且兩車道上行駛車輛重量不同，Fr.40肋位強橫梁承受彎矩大于Fr.21肋位強橫梁承受的彎矩，此外橫艙壁靠近內舷側部位和片體與連接橋交接處的欄桿應力也較大.各測點最大應力值均小于許用應力值，滿足結構強度要求，可安全營運.

大部分測點計算結果與測試結果的相差不超過10%，實橋測試結果與計算結果基本吻合.選取落灘片體測點的測試結果與工況5有限元計算結果進行比較，具體結果見表5.

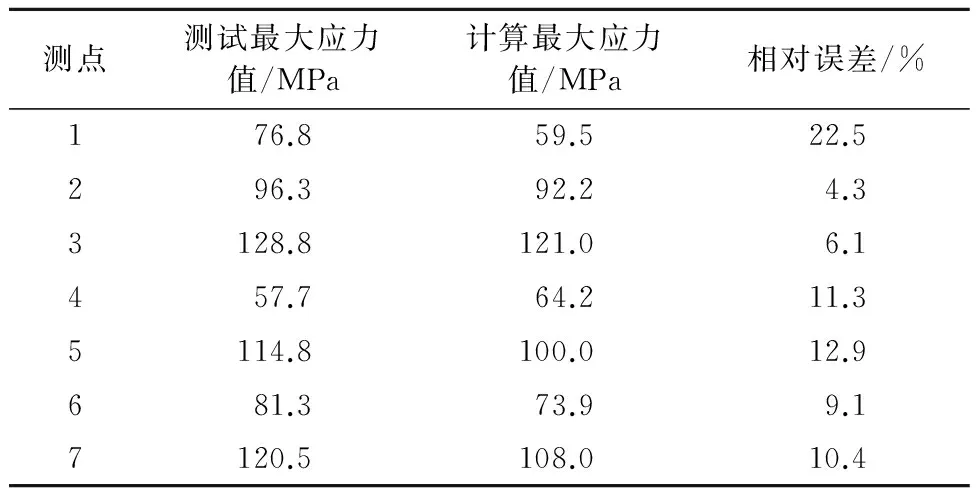
表5 落灘片體測試結果與計算結果比較

由表5可知，落灘片體上測點1的測試值與計算值比較相差較大，由于落灘片體的落灘狀況復雜，計算時考慮落灘片體底部全部落灘，而實際落灘片體為部分不均勻落灘，承壓舟首尾兩端落灘狀況不同，連接橋邊緣甲板強橫受力狀況惡劣.實際車輛的重量分布與計算時所取的車輛重量分布不同，以及計算所取掛車重量有誤差等各種因素，造成計算結果與測試結果有偏差.

5 結 論

1) 承壓舟浮橋在營運時，連接橋會承受較大的車輛載荷，車輛在不同位置時，連接器會承受橫彎、橫扭和彎扭組合作用，車道下方橫艙壁和連接橋上甲板強橫梁應力較大，根據計算結果合理改變橫艙壁厚度及甲板強橫梁尺寸，承壓舟滿足結構強度要求.

2) 承壓舟的連接橋底部設置的底封板的數目對結構強度影響較大，設置底封板能有效地增加連接橋結構強度，但當數目過多時，連接橋結構過強，車道下方的橫艙壁應力會變大.設計時應根據連接橋寬度合理選擇底封板數目.

3) 車道下方的單橫艙壁改為雙橫艙壁且厚度為6mm時能有效改善結構強度，但當繼續增加橫艙壁厚度時，橫艙壁隨著結構加強應力會減小，但相鄰的連接橋上強橫梁的應力會增加.

4) 計算結果和測試結果吻合較好，選取的典型計算工況能充分考慮承壓舟浮橋營運時連接橋承受的各種最惡劣狀況，選取的工況合理可靠.

5) 承壓舟浮橋在營運時，落灘片體實際可能為不均勻落灘，受力狀況較為復雜，計算時很難模擬實際落灘情況，這也是計算結果和測試結果相差原因之一.

[1]沈榮釗,周康錚.雙體承壓舟在經濟建設中的應用[J].山東交通科技,1993(3):168-175.

[2]中國船級社.鋼質內河船舶建造規范[S].北京:人民交通出版社,2016.

[3]ZHANG J, MIAO G P, ZHOU Z W. Simulink based simulation of the behavior of a ribbon pontoon bridge[J]. Journal of Marine Science & Application,2010,9(3):328-333.

[4]FU S X, CUI W C. Dynamic responses of a ribbon floating bridge under moving loads[J]. Marine Structures,2012,29:246-256.

[5]王丙,陳徐均,江召兵,等.帶式浮橋在不同移動荷載作用下的動力響應分析[J].應用力學學報,2013(1):43-48.

[6]孫奇,王丙,李聚軒,等.單個移動荷載作用下浮橋的動態響應[J].軍事交通學院學報,2016(5):80-84.

[7]姜玥,任慧龍.承壓舟結構強度計算方法研究[D].哈爾濱：哈爾濱工程大學,2010.

[8]王楠,任慧龍,王曉天.高寒地區浮橋環境載荷與強度評估[J]，武漢理工大學學報，2014，36(8)：589-596.

[9]裴志勇，鄭培培.千噸級雙向四車道承壓舟應力測試研究報告[R].武漢：武漢理工大學，2016.

Research on Structural Strength Direct Calculation of Pontoon Bridge

ZHENG Peipei1)PEI Zhiyong1,2)LIU Weiqin1,2)ZHAO Qinliang3)

(Key Laboratory of High Performance Ship Technology of Ministry of Education, Wuhan University of Technology, Wuhan 430063, China)1)(Departments of Naval Architecture, Ocean and Structural Engineering, School of Transportation, Wuhan University of Technology, Wuhan 430063, China)2)(Jinan Register of Shipping, Jinan 250014, China)3)

The pontoon bridge which has characteristics of lower cost, shorter construction, better economy and larger traffic flowing capacity has a wide application in un-navigable waters. However, there are no appropriate rules until now. Research on structural strength direct calculation of pontoon bridge is carried out. Five typical calculating cases are defined considering its structure form and actual loading conditions. The influence of transverse bulkhead arrangement and sealing plate at the bottom of the connection bridge on structural strength is discussed. Furthermore, dynamic test on the pontoon bridge is also performed. Calculation cases and calculation methods are validated by comparing the test results with the computational results.

pontoon bridge; calculation cases; structural strength; strength criteria; dynamic test

2017-03-13

U663.2

10.3963/j.issn.2095-3844.2017.03.032

鄭培培(1993—)：男，碩士生，主要研究領域為船體結構強度