對初中數學教學中教材使用的幾點思考
□胡方澤
(諸暨市趙家鎮初級中學,浙江諸暨 311819)
備課參考
對初中數學教學中教材使用的幾點思考
□胡方澤
(諸暨市趙家鎮初級中學,浙江諸暨 311819)
在新課程實踐中,廣大初中數學教師對教材使用進行了大膽的嘗試,積累了不少可貴的經驗.在新課程理念的引領下,教師們認真研讀教材,改變傳統的教學習慣,充分利用好教材例題,引導學生探索例題思路,加強對例題的探究與拓展,提高學生的數學能力.
初中數學;教材使用;數學能力
一、讀懂、悟透教材是構建高質量數學課堂的本原
1.確定教材的地位和作用.教材是教與學的依據,不以教材為基礎的數學課堂會失去方向,教學質量也沒有保障.要確定某節或某課時教材的地位和作用,教師須先確定整章內容在教材體系中所處的地位和作用,梳理整個教材體系,將教材內容分類歸納,把握整體的知識體系.再了解單元內課時與課時之間的聯系,對一節課在整章、整個教材體系中的位置和作用都做到心中有數.此外教師在關注教材的知識體系以外,還要從教材文本的表象信息中找出無形的數學思想方法這條暗線,細心體會編者的意圖.
2.讀懂教材所涉及的相關知識與教學要求.教師在領會課標理念與要求的基礎上研讀教材,在熟悉整個教材體系后,鉆研本節內容相關知識結構與聯系,同時還要關注知識背后的思想方法.例如《代數式的值》是浙教版數學教材七年級上冊第4章《代數式》中的第3節,是學生會列代數式后,經歷給定一個數求代數式的值的過程,它是后續學習方程、函數的重要基礎.教材以2001年中國申奧成功時莫斯科和北京的時間作為問題背景,引出“代數式的值”的概念.緊接著“做一做”這個欄目給出了類似的問題——倫敦和北京的時間差問題,最后給出了以下例題.
例 圓柱的體積等于底面積乘高,若用h表示圓柱的高,r表示底面半徑(如圖1),V表示圓柱的體積.
(1)請 用 字母 h,r,V 寫 出圓柱的體積公式.
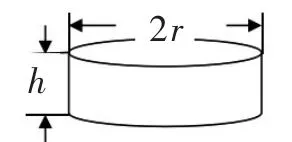
圖1
(2)求底面積半徑為 50cm,高為 20cm 的圓柱的體積.
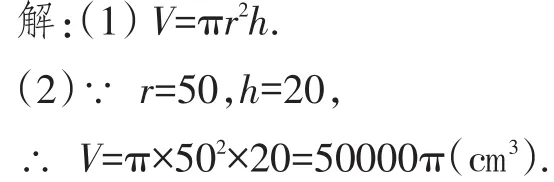
答:所求圓柱的體積為50000πcm3.
課程標準關于“代數式的值”的要求為:會求代數式的值;能根據特定的問題查閱資料,找到所需要的公式,并會代入具體的值進行計算.例1對應了課程標準中要求的內容.
二、重視教材中的概念引入 讓學生經歷對概念由感性到理性的認識
1.以生活素材為背景引入.在數學概念教學時,教師要恰當地選取生活素材,呈現給學生熟悉且與概念密切聯系的問題情境,讓學生從對具體問題的體驗中感知概念,形成感性認識,再通過對感性材料的觀察、分析,歸納和抽象出概念的特征,完成從具體到抽象的認知過程.
2.以原有概念為模型引入.數學中有許多概念存在著密切的聯系,它們不僅具有相似的特點,而且表述方式也類似,教師在新概念教學時可引導學生依據已有概念為模型,分析它們的結構特征,再引入新概念.如全等三角形的定義與相似三角形的定義,一元一次方程的定義與一元一次不等式的定義等.因此,在分式的概念引入時可類比分數的概念,同樣,對不等式性質的研究也可類比等式的性質引入.
三、充分利用教材例題 提高學生的數學能力
1.利用教材例題,引導學生反思感悟思想方法.浙教版數學教科書八年級下冊“6.3反比例函數的應用”,有以下例題.
例 設△ABC 中 BC 邊的長為 x(cm),BC 上的高線 AD 為 y(cm),△ABC 的面積為常數,已知y關于x的函數圖象過點(3,4).
(1)求y關于 x的函數表達式和△ABC的面積.
(2)畫出函數的圖象,并利用圖象,求當2<x<8時y的取值范圍.
本例第(2)題的解決中蘊含數形結合的基本思想和借助幾何直觀解決函數問題的常用方法,因此在例題解決后,可設如下問題引導學生思考,加深理解并拓展:第(1)題中得出函數解析式的依據是什么?第(2)題中根據給定的自變量的范圍求函數的范圍有哪幾個步驟?第(2)題中求 y的取值范圍,除了教科書上的方法外,還有別的方法嗎?如果已知函數的取值范圍,怎樣求相應的自變量的范圍?請結合本例中的函數,舉個具體的例子試一試.
通過上述第一問,讓學生掌握:依據實際問題中變量之間的數量關系可以求函數解析式、建立數學模型的方法.通過第二問,提煉和掌握用數形結合、借助幾何直觀求函數取值范圍的常用方法.通過第三、第四問,幫助學生在教科書的基礎上獲得進一步的提高,為高中的函數學習打下扎實的基礎.
2.利用教材例題,提高學生思維的品質.浙教版數學教科書八年級下冊“4.5 三角形的中線”有如下例題.
已知:如圖2,在四邊形ABCD中,E,F,G, H分別是AB,BC,CD,DA的中點.求 證 :四 邊 形 EFGH 是 平行四邊形.
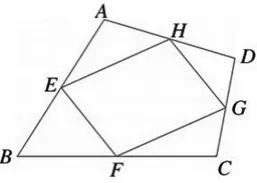
圖2
這是“中點四邊形”的問題,當學習了矩形、菱形、正方形后,可對這道例題作如下拓展和延伸.
(1)平行四邊形、矩形、菱形、正方形的中點四邊形分別是什么四邊形?
(2)當原四邊形具備什么條件時,中點四邊形會變成矩形,菱形,正方形?
(3)中點四邊形的周長、面積與原四邊形有何關系?
教師對上面的拓展和延伸,能使學生對特殊四邊形的判定方法有進一步深入的認識,對矩形、菱形、正方形這些特殊四邊形之間的區別和聯系更加清楚,幫助學生形成良好的網絡知識,以提高學生思維的品質,從而提高教學效率.這種從不同概念之間的異同和聯系入手進行拓展也是例題拓展的一個設計方向.
3.利用教材例、習題,讓問題解決的過程成為學生探究的過程.對于浙教版數學教科書九年級上冊“4.5 相似三角形的性質及其應用(2)”的作業題“5.有一塊三角形余料 ABC,它的邊BC=120cm,高線AD=80cm.要把它加工成正方形零件,使正方形的一邊在BC上,其余兩個頂點分別在AB,AC上.求加工成的正方形零件的邊長”.通過對問題的進一步研究,發現此題在解題方法和問題的拓展方面都有新的發現,教師應繼續引導學生進行探究和拓展.
探究1.若并排放置的兩個相等的小正方形組成的一個矩形,內接于△ABC(如圖3),則小正方形的邊長為多少?并排放置3個小正方形呢?如圖4,若并排放置的小正方形有n個,則這時小正方形的邊長又為多少?
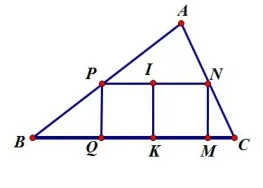
圖3
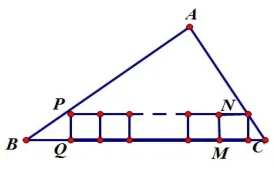
圖4
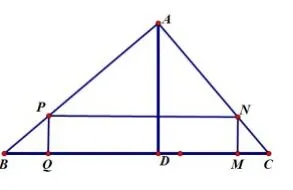
圖5
探究2.如圖5,若四邊形PQMN為△ABC的內接矩形.
(1)設 PQ=x,你能求出 PN 的長嗎?(用含x的代數式表示)
(2)記矩形PQMN的面積為S,求S的最大面積.
例題教學后,教師應經常提醒學生“是否還有別的更簡單的方法解決這個問題”“是否可以優化這個問題的解決過程”“你能應用這種解法解決類似的問題嗎”等類似問題,激發學生思考、創新的積極性.在教學方法上,教師可適當創設情境,結合動手操作的探究題,留給學生更多思考的時間和空間,讓學生自由地發表觀點,充分調動學生參與學習的積極性,在交流中發現學生的思維火花.

