某型高速飛行器非定常氣動力模擬研究
李智勞 李曉東 劉 凡
中國飛機強度研究所
某型高速飛行器非定常氣動力模擬研究
李智勞 李曉東 劉 凡
中國飛機強度研究所
湍流中充斥著大大小小的渦旋,湍流是以高頻擾動渦為特征的有旋的三維(有時是準二維)運動。湍流運動還由于分子粘性作用要耗散能量,只有不斷從外部供給能量,湍流才能維持,因此湍流還具有耗散性。一般認為,無論湍流運動多么復雜,非穩態的N-S(納維-斯托克斯)方程對于湍流的瞬時運動仍然是適用的。高速流動下的流場必須視為可壓縮流體,本文對其進行了計算,得到了流場的分布。本文的方法對后續研究超高速飛行器的非定常氣動力及由此所帶來的其它力學問題有很大的幫助。
湍流;可壓縮;非定常氣動力
1 引言
流體力學和其他學科一樣,是通過理論研究和實驗分析兩種基本手段發展起來的。很早就已經有理論流體力學和實驗流體力學兩大分支。理論分析是用數學的方法來求出問題結果。但能用數學方法求出結果的問題畢竟很少,計算流體力學正是為彌補分析方法的不足而發展起來的。
2 流體運動理論
2.1 流體運動的基本方程
在流體力學中可以將流體視為連續介質。對于牛頓流體其控制方程分別為
質量方程:

動量方程:

能量守恒控制方程為:

其中,ρ為流體密度;t為時間;u為流體速度矢量; 為Hamilton算子;

x1,x2,x3分別為笛卡爾坐標系下三個坐標變量;i,j,k分別為三個方向的單位矢量;f為作用在流體上的體積力;p為壓力;τ為流體的應力張量;

λ為流體第二粘度;μ為流體動力粘度;
δij為單位張量,i≠j時,δij= 0;i= j時,δij=1;
e為流體的內能,

對于理想氣體有,

CP為定壓比熱;T為溫度;q為熱通向量;

K為導熱系數;Wv為粘性動力做功項,

Ek為動能,定義為,


Qv為單位流體熱量的增加量;
氣體狀態方程為

理想氣體的狀態方程為:對于一般流體可以得到

其中R為氣體常數;
設流體靜止時,任意一點的壓強是p0,平均壓強是
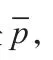
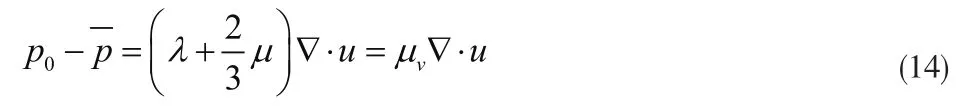

其中,μv為容積粘度采用斯托克斯假設μv=0,則有

將式(15)代入(2)得到
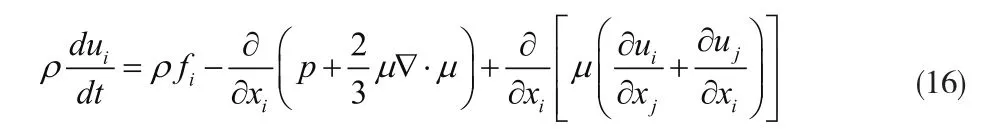
式(16)即為N-S(納維-斯托克斯)方程。
2.2 湍流流動的模擬
湍流是一種復雜的非穩態流動,在湍流中,流體的各種物理參數,如速度、壓力、溫度等都隨時間與空間發生隨機的變化,但這些量的統計平均值卻是有規律的。由于湍流的復雜性,目前還無法對其給出一個嚴格的定義,一般認為湍流有以下幾個特征:不規則性或隨機性,擴散性,大雷諾數性質。湍流中充斥著大大小小的渦旋,湍流是以高頻擾動渦為特征的有旋的三維(有時是準二維)運動。湍流運動還由于分子粘性作用要耗散能量,只有不斷從外部供給能量,湍流才能維持,因此湍流還具有耗散性。一般認為,無論湍流運動多么復雜,非穩態的N-S(納維-斯托克斯)方程對于湍流的瞬時運動仍然是適用的。
3 算例
3.1 建立模型及計算域
飛行器的尺寸如圖1所示;模型如圖2所示;計算域模型如圖3所示,將計算域建為柱形,以適應高速流動情況下的壓力遠場邊界條件。計算域的長度為33m,直徑為0.6m。圖4為計算域的網格劃分,單元仍然采用六面體單元。
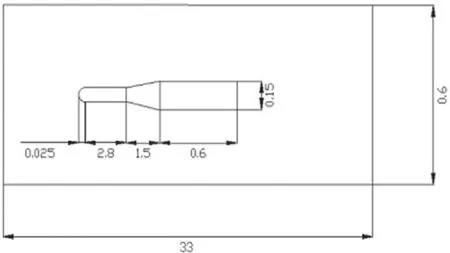
圖1 模型尺寸圖(單位:m)

圖2 飛行器模型圖
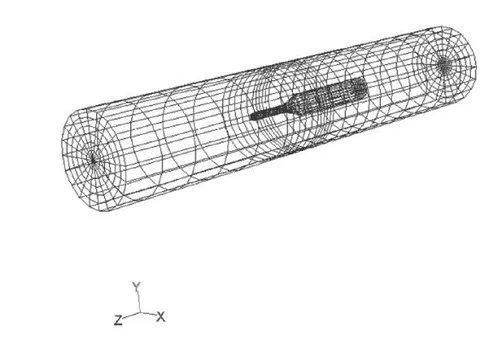
圖4 網格圖
3.2 流場計算及結果分析
FLUENT軟件穩態計算的相關設置如表1所示,瞬態計算的相關設置如表2所示。高馬赫數的流動應視為可壓縮流動,氣體視為理想氣體,密度按照氣體狀態方程求解。邊界條件采用壓力遠場邊界條件(Pressure-Far-Field),遠場來流馬赫數為1馬赫。
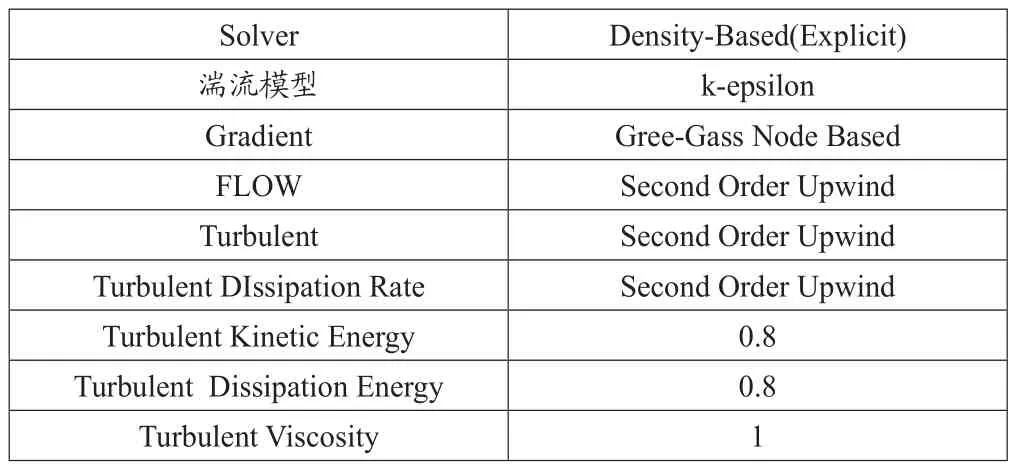
表1 穩態計算的相關設置

表2 瞬態計算的相關設置
流場計算的結果如圖5,6所示,圖5為飛行器表面的靜壓分布圖,最大值為7.60×104MPa,圖6為流場各節點的流速分布圖,流速的最大值為493m/s。

圖5 飛行器表面靜壓分布圖

圖6 飛行器表面及流體域速度矢量分布圖
4 結論
FLUENT對流場的求解主要有三種方法,分別為密度基-顯式,密度基-隱式,壓力基-隱式。其中密度基解法主要用來求解高馬赫數的可壓縮流動。密度基求解器是從原來的耦合求解器發展而來,它是同時求解連續性方程,動量方程以及能量組分方程,然后按順序求解其它標量方程。本文運用FLUENT軟件提供的密度基-顯式計算了來流速度為1馬赫時的飛行器流場,給出了流場分布,對后續研究超音速,高超音速的流場問題具有重要的指導意義。
[1]張俊明 姜連田.FLUENT入門與進階教程[M].北京:北京理工大學出版社,2008.
[2]邢靜忠 王永崗 陳曉霞.ANSYS7.0分析實例與工程應用[M].北京:機械工業出版社,2004.
[3]肖紅林.槽道湍流的大渦模擬[D].天津大學,2004.
[4]H.-J.Kim,S.Lee,N.Fujisawa.Computation of unsteady flow and aerodynamic noise of NACA0018 airfoil using large-eddy simulation,International Journal of Heat and Fluid Flow,27(2006):229-242.
[5]Philip J M,Lyle N L,AshokB,Wang Q.A parallel three-dimentional computional aeroacoustics method using nonlinear disturbance equations.J Computional Physics,1997,133:56-74.
[6]Goldstein M E.Aeroacoustics of Turbulent Shear Flows[J].Annu Review Fluid Mechanics,1984,16:263-285.

