考慮非線性油膜力的裂紋轉子動力學特性仿真

向 玲， 高雪媛

(華北電力大學 機械工程系，河北保定 071003)

?

考慮非線性油膜力的裂紋轉子動力學特性仿真

向 玲， 高雪媛

(華北電力大學 機械工程系，河北保定 071003)

在考慮裂紋軸時變剛度和非線性油膜力的基礎上，建立了含裂紋故障的雙盤轉子-軸承系統的動力學模型，采用數值積分方法對其求解，結合分岔圖、軸心軌跡圖、Poincaré截面圖和三維譜圖等，分析了轉速、裂紋深度和不平衡對系統響應、分岔情況以及穩定性的影響.結果表明：該類系統出現了多周期、擬周期、混沌等豐富的非線性動力學行為；在裂紋較深的情況下，在較低轉速便會發生倍周期分岔和多周期運動，系統的非線性和不穩定性增強；不平衡力的增大簡化了系統的動力學行為，使系統失穩滯后，但不影響油膜振蕩.

轉子動力學； 裂紋； 非線性油膜力； 分岔； 混沌

由于轉子材料本身的缺陷和長時間的工作，會逐漸產生疲勞裂紋，進而擴展，導致轉軸剛度降低，從而引起其橫向振動變大，影響機組的正常工作與安全.近年來，國內外學者對含有裂紋故障的轉子進行了一系列研究[1-5].甕雷等[6]研究了含汽輪機非線性間隙氣流激振力的裂紋轉子，討論了該激振力和裂紋深度對轉子-軸承系統振動響應特性的影響.何成兵等[7]建立了剛性支承的純彎曲振動、彎扭耦合振動和軸承支承的彎扭耦合振動3種裂紋轉子模型，對比分析了系統響應的分岔、混沌特性.Ricci等[8]提出了一種新的多自由度裂紋轉子模型，采用Floquet理論討論了各向異性和裂紋位置對系統穩定性的影響.秦衛陽等[9-10]以雙盤懸臂裂紋轉子為模型，主要分析了不同參數對系統進入混沌道路的影響.筆者主要以對稱布置的雙盤轉子為模型，更為全面地分析了參數變化對系統運動形式、頻率特征的影響.劉長利等[11]采用有限元方法建立了雙盤雙呼吸裂紋轉子系統的動力學模型，給出了不同裂紋深度和裂紋夾角對轉子振動響應的影響.于海等[12]通過改進的正交模態分解技術(POD)將26自由度的含有裂紋故障的高維系統降為具有2個自由度含有裂紋故障的低維模型，并利用C-L方法對其進行了分岔分析.

已有的關于含裂紋故障的雙盤轉子-軸承系統的文獻較少，大部分又是用有限元法而非數值方法.因此，筆者建立了油膜支承下含裂紋故障的雙盤轉子系統的動力學模型，考慮轉軸的裂紋時變剛度，采用Runge-Kutta法進行求解，討論轉速、裂紋深度以及偏心量變化對系統動力學特性的影響，為實際中轉子-軸承系統的振動特性分析提供了一定的理論依據.

1 含裂紋故障的轉子系統模型

所研究的含裂紋故障的雙盤轉子-軸承系統，轉子兩端采用對稱結構的滑動軸承支承，如圖1所示.Oi(i=1,4)為軸端軸承內瓦幾何中心，Oi(i=2,3)為轉子幾何中心；轉子在軸承處的集中質量為m1和m4，轉軸中央圓盤等效質量為m2和m3，并在靠近左端圓盤處有一橫向弓形裂紋，如圖1所示；k為無裂紋時轉軸剛度，ci(i=1,4)為轉子在軸承處的結構阻尼，ci(i=2,3)為轉子圓盤處的結構阻尼.Fxi(i=1,4)和Fyi(i=1,4)為滑動軸承作用在轉軸上的非線性油膜力，軸承半徑為R，長度為L，軸承間隙為c.

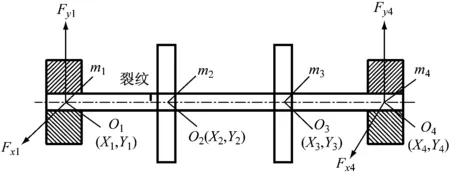
圖1 含裂紋故障的雙盤轉子-軸承系統

1.1 裂紋模型

圖2所示為轉軸裂紋處橫截面，其中xoy為絕對坐標系，ξo′η為固定在圓盤上并隨圓盤轉動的坐標系，o′ξ為裂紋擴展方向，o′η為裂紋擴展垂直方向.ψ為轉子的渦動角，θ=ωt為自轉角，其中，ω為轉動角頻率，φ=θ-ψ為轉渦差角，e為質量偏心，β為裂紋方向與不平衡方向之間的夾角.則在考慮呼吸裂紋后的轉軸剛度矩陣[13]可表示為

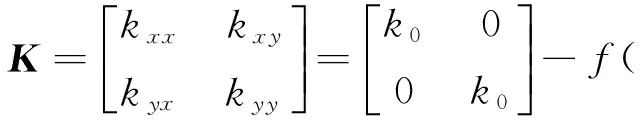
(1)

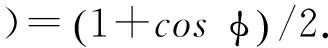
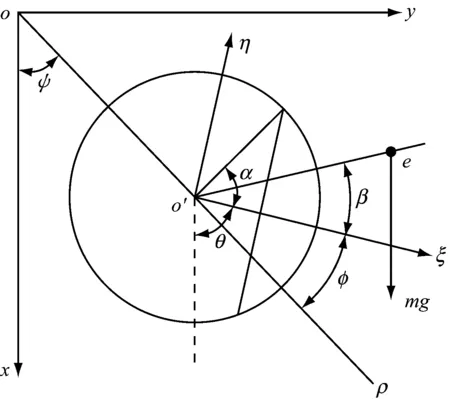
圖2 開閉裂紋模型示意圖

1.2 油膜力模型

本文滑動軸承處所產生的油膜力具有強非線性，理論分析中采用經典的Capone圓軸承理論[14]，該模型精度較高，具體表達式如下：

(2)

式中：fx、fy分別為無量綱非線性油膜力在x與y方向上的分量；σ為Sommerfeld修正數.

(3)

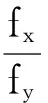
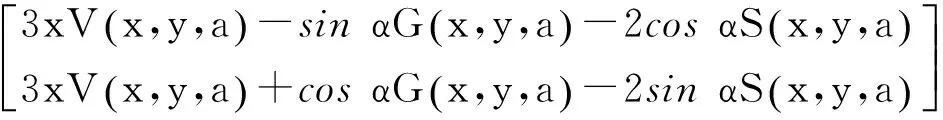
(4)

其中，

式中:x，y為軸承位移；μ為潤滑油黏度.

1.3 轉子系統運動微分方程

假設含裂紋故障的雙盤轉子-軸承系統兩端軸頸的徑向位移為x1、y1、x4和y4，中央圓盤處的徑向位移為x2、y2、x3和y3，忽略陀螺力矩和扭轉振動，只考慮系統的橫向振動，則系統的運動微分方程如式(6)所示.

2 系統運動微分方程求解

2.1 系統運動微分方程的無量綱處理

式(6)中給出了含裂紋故障的雙盤轉子-軸承系統的運動微分方程，綜合考慮了剛度的變化和非線性油膜力的影響，將式(1)中的剛度模型和式(4)中的油膜力代入式(6)中，同時引入無量綱變換：

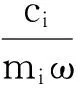
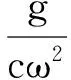
則無量綱后的運動微分方程如式(7)所示.

(6)

(7a)

(7b)

2.2 參數設置

表1給出了含裂紋故障的雙盤轉子-軸承系統的主要參數.由于式(7)(包括式(7a)和式(7b))表示一個強非線性系統，采用四階Runge-Kutta法對其進行數值積分求解，并舍去前300個周期的結果以消除瞬態響應，進而得到系統的分岔圖等.

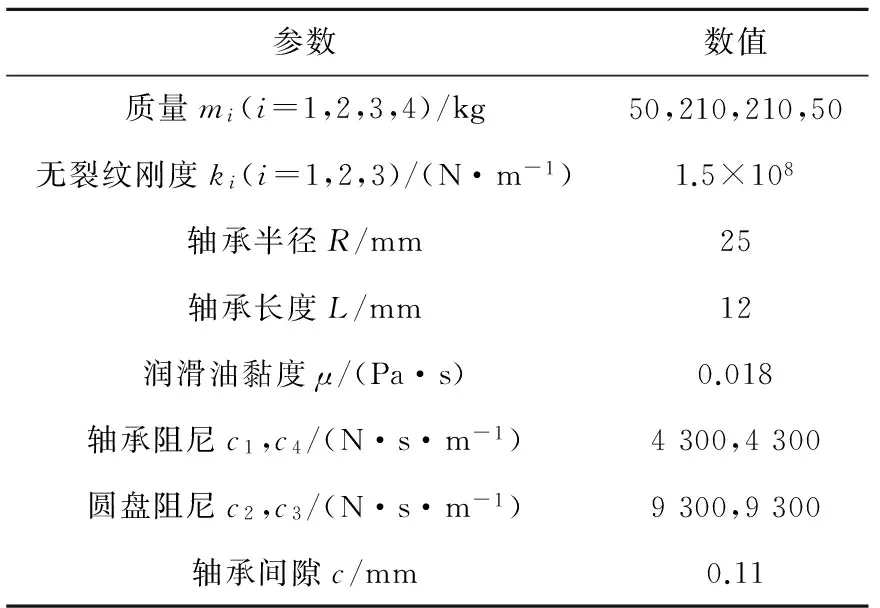
表1 系統主要參數

3 仿真與分析

3.1 轉速對系統響應的影響

圖3給出了系統響應隨轉速變化的分岔圖，此時裂紋剛度變化比Δkζ=0.1，偏心量取0.1 mm，其他參數如表1所示.由圖3可知，系統歷經P-1→ P-2→P-4→混沌→P-8→P-4→P-2→多周期→混沌.系統發生倍周期分岔的分岔點轉速為ω=390 rad/s，開始出現油膜渦動，從單周期運動進入到雙周期P-2運動，如圖4(a)所示，ω=400 rad/s時，時域波形為周期信號，軸心軌跡為兩圓疊交，頻譜圖上存在油膜失穩頻率、基頻以及倍頻nX/2(n=3,4,5…)，且油膜失穩頻率為基頻的0.5倍，Poincaré截面圖上存在2個孤立的相點.

而在轉速ω=855 rad/s時，系統發生Hopf分岔進入擬周期運動，如圖4(c)所示，當ω=1 000 rad/s時，軸心軌跡呈花環狀，頻譜圖上存在油膜失穩頻率、基頻、基頻的分數階和高階倍頻，油膜失穩頻率約為基頻的0.38倍，Poincaré截面圖上出現“鎖相”現象，此時油膜渦動發展成為油膜振蕩，故障加重，系統進行擬周期運動.在轉速范圍1 660～1 705 rad/s內，系統出現短暫的P-3運動，圖4(d)中ω=1 670 rad/s時，時域圖規則，頻譜圖上主要是油膜振蕩頻率和基頻，油膜振蕩頻率為基頻的0.33倍，Poincaré截面圖鎖相為3個相點.

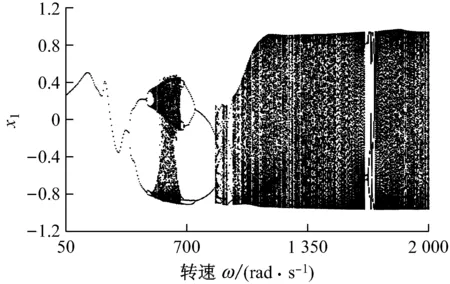
圖3 系統響應隨轉速變化的分岔圖

3.2 裂紋深度對系統響應的影響

圖5、圖6分別為Δkζ=0.5和0.9時系統響應隨轉速變化的分岔圖.由圖5和圖6可知，系統首次分岔點分別變為ω=455 rad/s和ω=340 rad/s，結合圖3可知系統首次分岔點的轉速先增大后減小，說明裂紋從輕度發展到中度過程中，裂紋的存在會干擾油膜渦動的形成，而在裂紋進行到重度情況時，系統不穩定性增強，在較低轉速時便會發生倍周期分岔和多周期運動.另外，裂紋深度的增加對系統響應的影響還表現在中高速區域.對比圖3、圖5和圖6可以看出，隨著裂紋深度的增加，系統中速區發展為更明顯的多周期、擬周期交替運動；高速區的P-3運動窗口不僅變寬，而且有所前移.這些現象均說明裂紋的發展會導致系統的非線性和不穩定性增強.

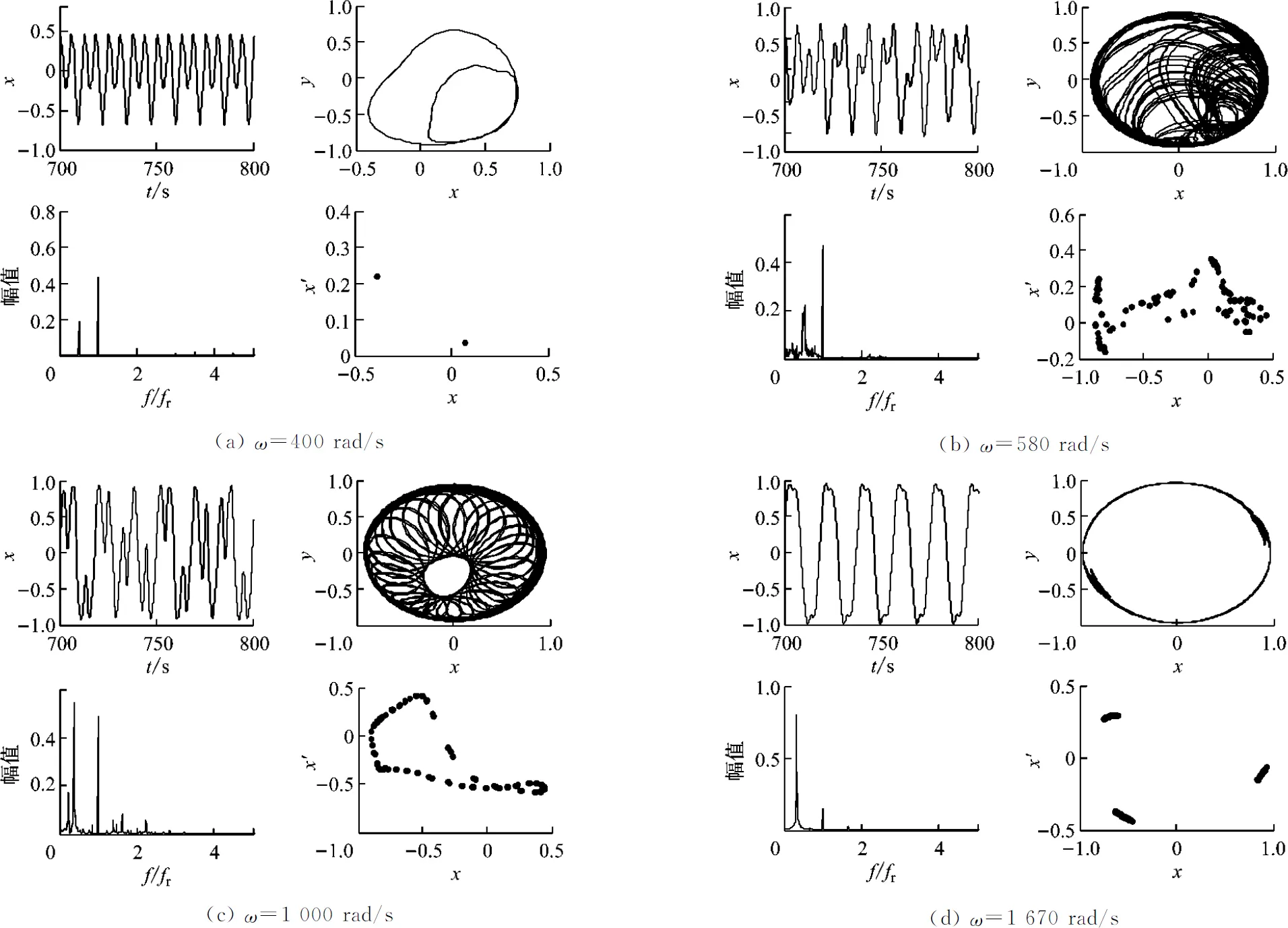
圖4 不同轉速下的系統響應

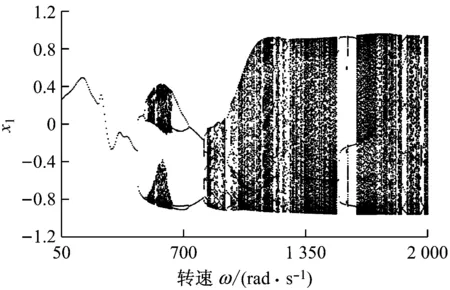
圖5 Δkζ=0.5時系統響應隨轉速變化的分岔圖

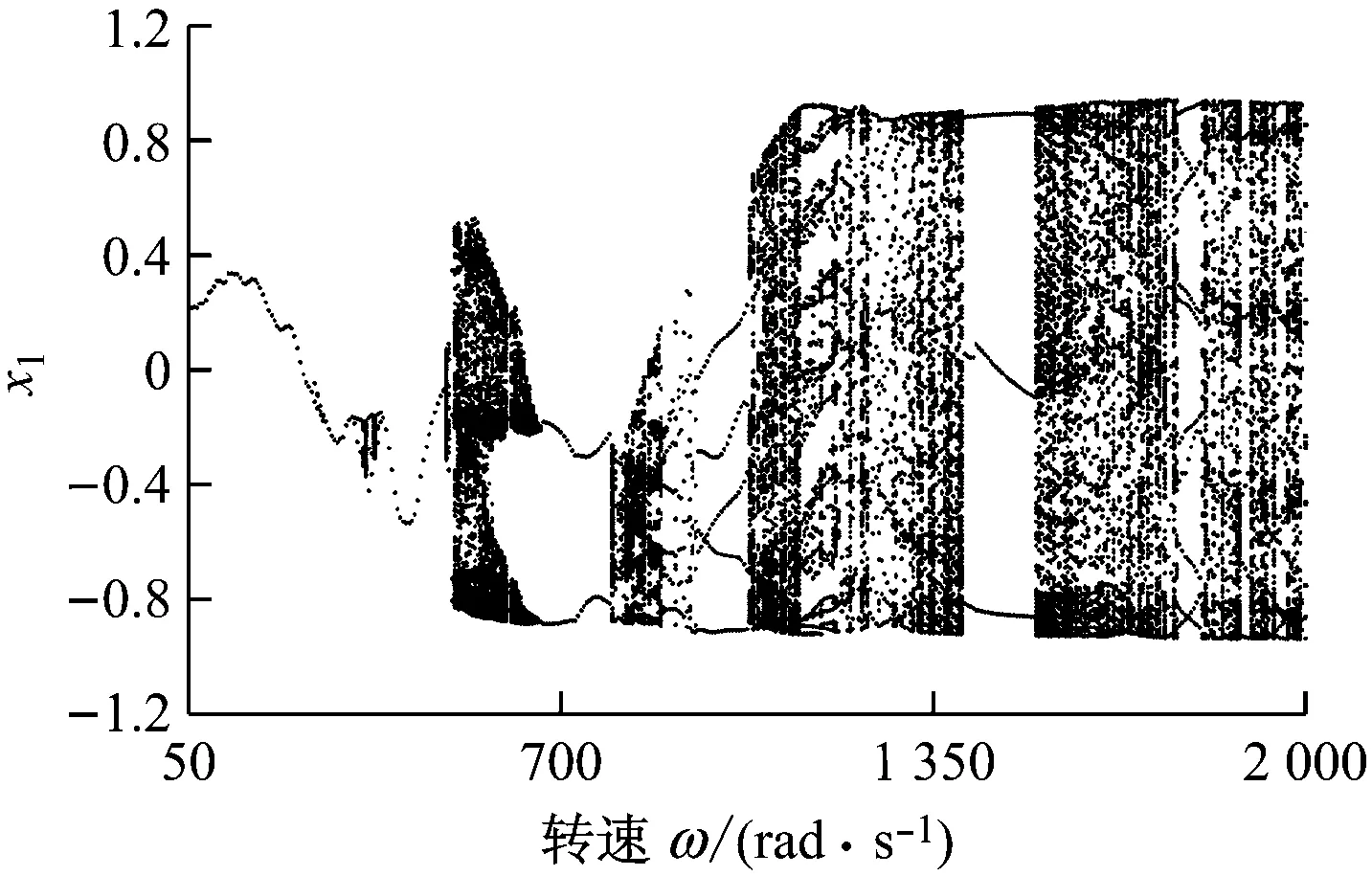
圖6 Δkζ=0.9時系統響應隨轉速變化的分岔圖

3.3 不平衡對系統響應的影響

在實際轉子系統中，由于轉子本身加工誤差導致的質量不均勻、安裝偏心等原因，不可避免的存在轉子不平衡情況，此處將分析不平衡力對含裂紋故障的雙盤轉子-軸承系統振動響應的影響，而在一定轉速下，偏心量的大小決定了不平衡力的大小.

圖7和圖8為裂紋剛度變化比Δkζ=0.1，偏心量e=0.2 mm和0.3 mm時的系統分岔圖.對比圖3、圖7和圖8可知，隨偏心量的增大，不平衡力也會增大，較大的不平衡力會簡化系統的運動形式，系統的分岔情況相對變得簡單.從圖3、圖7和圖8可以看出，系統首次分岔點的轉速發生后移，從圖3中的ω=390 rad/s變為ω=850 rad/s和ω=1 030 rad/s，說明偏心量的增大會使系統失穩滯后.其次，原中速區的混沌窗口縮小并且后移，高速區的P-3運動窗口也發生后移.圖9給出了偏心量取0.1 mm、0.2 mm和0.3 mm時系統的三維譜圖，圖中可觀察到油膜失穩頻率f0、基頻fr以及基頻的多個高階倍頻(fr+f0,2fr).此外，偏心量的增大使出現油膜渦動頻率的轉速增大，但并沒有影響油膜振蕩，這一點與圖7和圖8的結果相符.

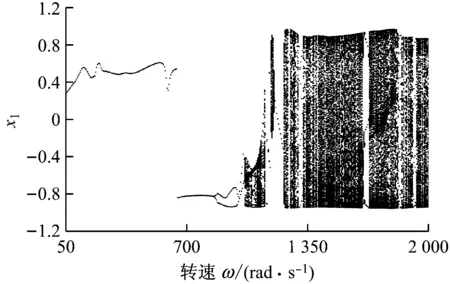
圖7 e=0.2 mm時系統響應隨轉速變化的分岔圖

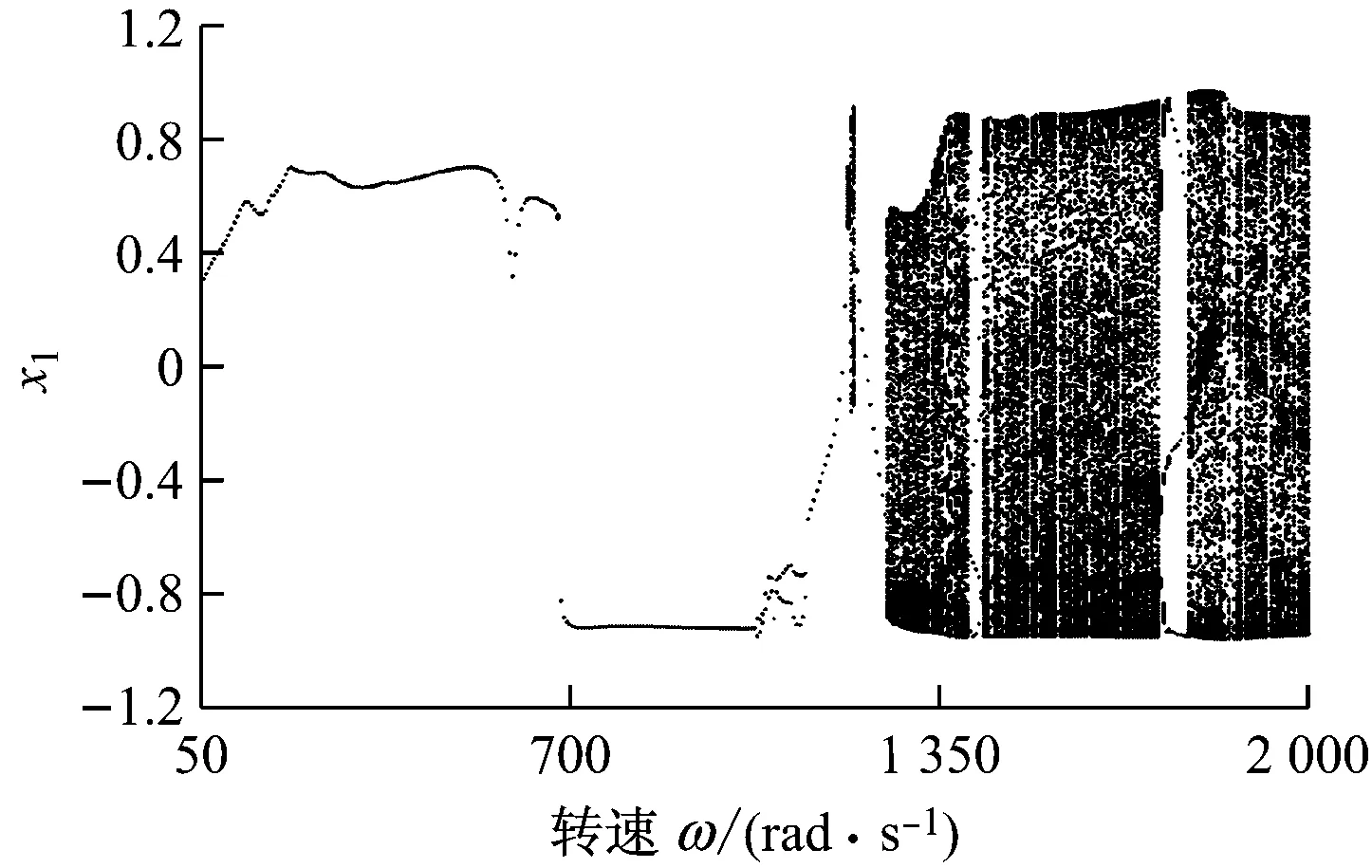
圖8 e=0.3 mm時系統響應隨轉速變化的分岔圖

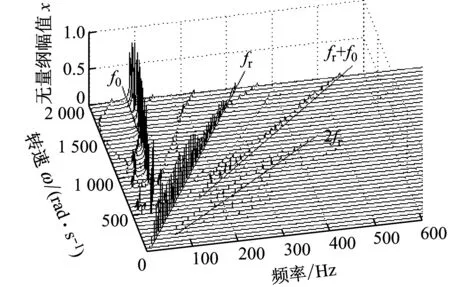
(a) e=0.1 mm

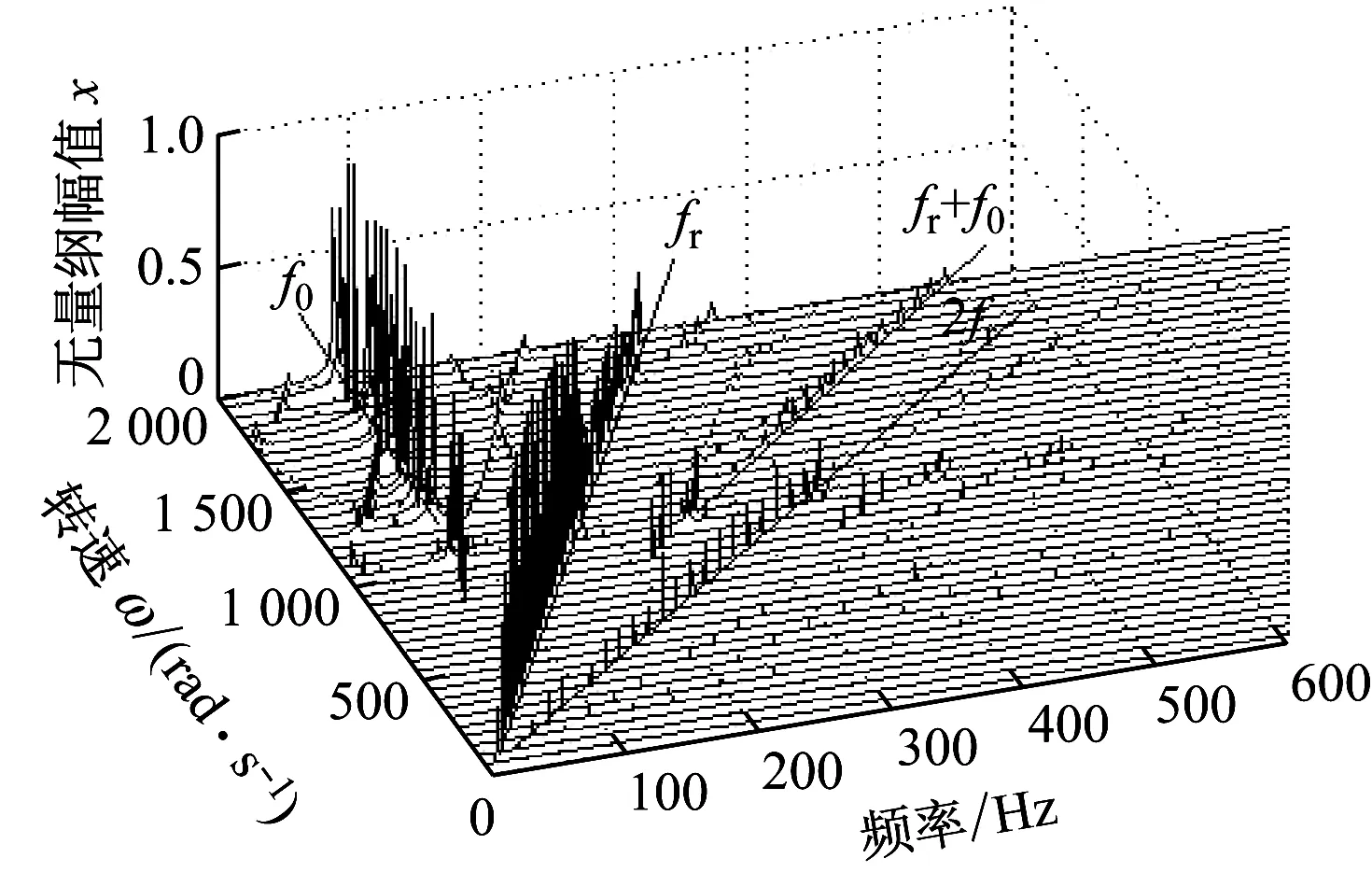
(b) e=0.2 mm

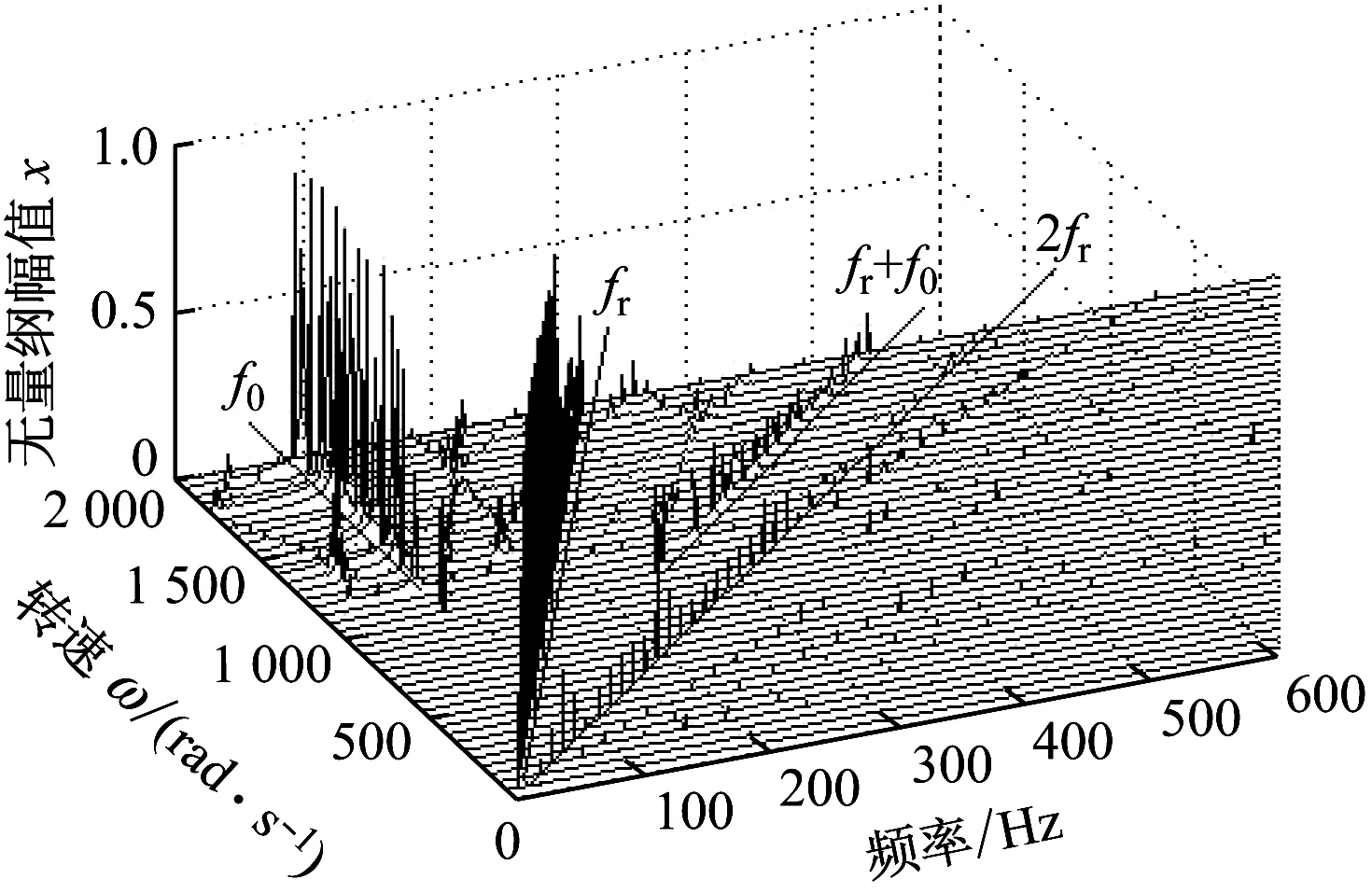
(c) e=0.3 mm

4 結 論

(1) 在轉速的影響下，系統出現了多周期、擬周期、混沌等豐富的動力學行為，并歷經多次倍周期分岔進入混沌運動和Hopf分岔進入擬周期運動.

(2) 隨著裂紋深度的增加，裂紋干擾了油膜渦動的形成，使系統首次分岔點的轉速增大，但在裂紋較深的情況下，在較低轉速便會發生倍周期分岔和多周期運動，并且在中速區發生更加明顯的多周期、擬周期交替運動，系統的非線性和不穩定性增強.

(3) 不平衡力的增加會簡化系統的非線性動力學行為，使系統失穩滯后，且原中速區的混沌窗口會縮小、后移.后續將在轉子試驗臺上進行相關試驗，研究各參數變化對系統響應的影響，以對比、驗證該模型下的數值計算結果.

[1] DIMAROGONAS A D. Vibration of cracked structures: a state of the art review[J]. Engineering Fracture Mechanics, 1996, 55(5): 831-857.

[2] SINOU J J, LEES A W. The influence of cracks in rotating shafts[J]. Journal of Sound and Vibration, 2005, 285(4/5): 1015-1037.

[3] 朱厚軍, 趙玫, 王德洋. Jeffcott裂紋轉子動力特性的研究[J]. 振動與沖擊, 2001, 20(1): 1-4.

ZHU Houjun, ZHAO Mei, WANG Deyang. A study on the dynamics of a cracked Jeffcott rotor[J]. Journal of Vibration and Shock, 2001, 20(1): 1-4.

[4] 史進淵. 核電汽輪機轉子在低周疲勞與高周疲勞交互作用下裂紋擴展壽命的研究[J]. 機械工程學報, 2015, 51(22): 152-158.

SHI Jinyuan. Study on crack propagation life under low cycle fatigue and high cycle fatigue of nuclear steam turbine rotors[J]. Journal of Mechanical Engineering, 2015, 51(22): 152-158.

[5] 宋光雄, 陳松平, 宋君輝, 等. 汽輪發電機組轉子裂紋故障研究及分析[J]. 動力工程學報, 2012, 32(4): 289-295.

SONG Guangxiong, CHEN Songping, SONG Junhui, et al. Cause analysis of rotor cracks in turbine-generator units[J]. Journal of Chinese Society of Power Engineering, 2012, 32(4): 289-295.

[6] 甕雷, 楊自春, 曹躍云. 汽輪機非線性間隙氣流激振力作用下含裂紋轉子的振動特性研究[J]. 振動與沖擊, 2016, 35(5): 89-95.

WENG Lei, YANG Zichun, CAO Yueyun. Bifurcation characteristic of a cracked rotor-bearing system under air-exciting forces of steam turbine[J]. Journal of Vibration and Shock, 2016, 35(5): 89-95.

[7] 何成兵, 顧煜炯, 宋光雄. 裂紋轉子彎扭耦合振動非線性特性分析[J]. 振動與沖擊, 2012, 31(9): 33-38.

HE Chengbing, GU Yujiong, SONG Guangxiong. Nonlinear analysis on coupled flexural and torsional vibrations of cracked rotor[J]. Journal of Vibration and Shock, 2012, 31(9): 33-38.

[8] RICCI R, PENNACCHI P. Discussion of the dynamic stability of a multi-degree-of-freedom rotor system affected by a transverse crack[J]. Mechanism and Machine Theory, 2012, 58: 82-100.

[9] 秦衛陽, 孟光, 任興民. 雙盤裂紋轉子的非線性動態響應與混沌[J]. 西北工業大學學報, 2002, 20(3): 378-382.

QIN Weiyang, MENG Guang, REN Xingmin. On nonlinear response of a cracked rotor with two disks[J]. Journal of Northwestern Polytechnical University, 2002, 20(3): 378-382.

[10] 陳宏, 李鶴, 張曉偉, 等. 雙盤懸臂裂紋轉子-軸承系統的動力學分析[J]. 振動工程學報, 2005, 18(1): 113-117.

CHEN Hong, LI He, ZHANG Xiaowei, et al. Dynamics analysis of a dual-disk over-hung rotor-bearing system with crack[J]. Journal of Vibration Engineering, 2005, 18(1): 113-117.

[11] 劉長利, 周邵萍, 江君, 等. 雙盤雙呼吸型裂紋轉子的非線性動力學特性[J]. 振動: 測試與診斷, 2012, 32(S1): 136-140.

LIU Changli, ZHOU Shaoping, JIANG Jun, et al. Nonlinear dynamics analysis of double-disc rotor with two breathing cracks[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(S1): 136-140.

[12] 于海, 陳予恕, 曹慶杰. 多自由度裂紋轉子系統非線性動力學特性分析[J]. 振動與沖擊, 2014, 33(7): 92-98.

YU Hai, CHEN Yushu, CAO Qingjie. Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system[J]. Journal of Vibration and Shock, 2014, 33(7): 92-98.

[13] 劉元峰, 趙玫, 朱厚軍. 考慮碰摩的裂紋轉子非線性特性研究[J]. 振動工程學報, 2003, 16(2): 203-206.

LIU Yuanfeng, ZHAO Mei, ZHU Houjun. Nonlinear characteristics of a cracked rotor with rub-impact[J]. Journal of Vibration Engineering, 2003, 16(2): 203-206.

[14] DING Q, COOPER J E, LEUNG A Y T. Hopf bifurcation analysis of a rotor/seal system[J]. Journal of Sound and Vibration, 2002, 252(5): 817-833.

Simulation on Dynamic Characteristics of a Cracked Rotor Considering Nonlinear Oil Film Force

XIANG Ling, GAO Xueyuan

(Department of Mechanical Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)

Considering the time varying stiffness and nonlinear oil film force, a dynamic model was established for the double disc rotor-bearing system with crack faults, and subsequently numerical integration method was used to solve the model, so as to study the effects of rotating speed, crack depth and unbalance force on the response, instability and bifurcation of the system by using bifurcation diagram, axis orbits, Poincaré maps and cascade spectrum. Results show that when the rotating speed changes, rich nonlinear dynamic behaviors would occur to the system, such as multiple periodic, quasi-periodic and chaotic motions. Under deep crack conditions, double period bifurcation and multi period motion would appear at a lower speed, when the system nonlinearity and instability tend to be enhanced. The increase of unbalance force simplifies the dynamic behavior of the system, makes the appearance of system instability lag behind, but does not affect the oil-whip.

rotor dynamics; crack; nonlinear oil film force; bifurcation; chaos

2016-06-20

2016-07-19

國家自然科學基金資助項目(51675178)

向 玲(1971-),女,湖北隨州人,教授,博士,研究方向為非線性動力學和故障診斷.電話(Tel.)：15032496266; E-mail：ncepuxl@163.com.

1674-7607(2017)06-0454-07

TH113

A

470.30