基于反向學習的跨種群差分進化算法

張 斌，李延暉，郭 昊

華中師范大學 信息管理學院，武漢 430079)(*通信作者電子郵箱hbguohao@163.com)

基于反向學習的跨種群差分進化算法

張 斌，李延暉，郭 昊*

華中師范大學 信息管理學院，武漢 430079)(*通信作者電子郵箱hbguohao@163.com)

針對差分進化(DE)算法存在的尋優精度低、收斂速度慢等問題，借鑒混沌分散策略、反向學習策略(OBL)以及跨種群并行機制，提出一種基于反向學習的跨種群差分進化算法(OLCPDE)。采用混沌分散策略進行種群初始化，將種群劃分為精英種群和普通種群，對兩個子種群分別采用標準的差分進化策略和基于反向學習的差分進化策略；同時，為進一步提高算法對單峰函數的求解精度和穩定性，采用了一種跨種群的差分進化策略，運用三種策略對子種群進行操作，達到共同進化的目的。實驗獨立運行30次，OLCPDE在12個標準的測試函數中，有11個函數都能穩定地收斂到全局最優解，優于對比算法。實驗結果表明，OLCPDE收斂精度高，能有效避免陷入局部最優點。

差分進化；反向學習；跨種群；混沌搜索；函數優化

0 引言

差分進化(Differential Evolution, DE)算法[1]是基于群體差異的啟發式優化算法，其原理簡單、受控參數少、魯棒性強，易于理解和實現[2]。DE算法作為一種簡單實用的全局搜索算法，已被證明是求解非線性、不可微和超高維等復雜函數的有效手段[3]，在科學研究與實際工程領域都得到了廣泛的應用[4]。

類似于其他的進化算法，DE算法也存在著早熟和收斂速度過慢的現象，為了解決這些問題，國內外很多學者對DE算法進行了大量的改進，算法的改進主要聚焦在三個方面，一是對參數的選取機制的研究，如Brest等[5]引入自適應縮放因子(Factor, F)和交叉概率(Crossover Rate, CR)，提出一種參數自適應的差分進化算法;汪慎文等[6]通過改變變異算子的學習方式，提出樸素差分進化算法。二是對差分變異策略的研究，如呂銘晟等[7]將標準差分進化算法的兩種變異策略串行組合，提出多變異策略差分進化算法。三是DE與其他具有某種優良特性的策略的集成，如王叢佼等[8]采用DE標準框架，當群體適應值方差小于一定閾值時，引入極值優化算法，提出基于極值優化的混合差分進化算法；匡芳君等[9]設置初始種群為隨機雙種群，分別采用混沌差分進化算法和混沌粒子群優化算法協同尋優，提出混沌差分進化粒子群協同優化算法；張大斌等[10]在魚群算法快速收斂的基礎上引入差分進化算法，提出基于差分進化的魚群算法。學者們的改進不同程度地提升了DE的收斂性能，然而DE及其改進算法依然存在收斂精度不高、對不同特征的基準測試函數魯棒性不好等問題，例如文獻[5-8]的算法在病態的Rosenbrock函數上均表現不佳。

本文將混沌分散策略和反向學習機制引入差分進化算法中，設計了一種基于反向學習的跨種群差分進化算法 (Cross-Population Differential Evolution algorithm based on Opposition-based Learning, OLCPDE)。該算法通過混沌分散策略產生初始種群，按適應度值大小將種群劃分為精英種群和普通種群，對精英種群采用標準的DE/best/1/bin差分進化策略，對普通種群采用反向學習改進的DE/rand/2/bin差分進化策略；為了增加算法的魯棒性，提高算法對單峰函數的求解精度和穩定性，同時采用了跨種群的DE/best/1/bin差分進化策略，借助種群間的并行機制和多種策略，以達到提高收斂速度，增強全局搜索能力的目的。通過選取測試函數進行尋優仿真驗證了算法具有較高的收斂速度和全局搜索能力。

1 標準差分進化算法

DE算法是一種基于實數編碼的群體優化算法，與其他進化算法類似，首先需要將種群初始化，然后對種群個體進行交叉、變異和選擇操作，通過多次迭代，最終使種群個體趨于全局最優解。差分進化算法的主要操作如下：

1)種群初始化。令Xi(t)=(xi1,xi2,…,xiD)為第t代種群的第i個個體，根據式(1)在可行域內隨機產生種群規模為NP，個體分量為D的初始種群X(0)。

i=1,2,…,NP,j=1,2,…,D

(1)

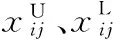
2)變異操作。變異操作為差分進化算法的核心，從種群中隨機選擇一個個體Xr1，作為待變異個體，再隨機選擇兩個個體Xr2，Xr3(NP≥4)作為擾動個體，根據式(2)，將這兩個個體的向量差縮放后與待變異個體進行向量合成，得到變異后的個體Ui。

uij(t+1)=xr1j(t)+F·(xr2j(t)-xr3j(t));

r1≠r2≠r3

(2)

其中：F為縮放比例因子，通常取值為[0.5,1]。

3)交叉操作。依式(3)，將變異后的個體和當前的演化個體以離散交叉的方式進行交叉操作生成中間個體Ci(t+1)，以提高種群多樣性。

cij(t+1)=

(3)

其中：rand(D)是區間[1,D]的隨機整數，CR∈[0,1]是交叉概率。

4)選擇操作。根據式(4)，對中間個體和當前個體之間進行貪婪選擇，通過計算個體目標函數值，將其進行比較，選擇適應度大的作為下代種群個體。

(4)

此外，DE算法還有多種差分策略，以上的基本差分算法實質上采用的是DE/rand/1/bin策略，除此之外，還有很多常用和經典的差分策略，如本文后續部分使用到的差分策略是DE/best/1/bin和DE/rand/2/bin，如式(5)和式(6)。

uij(t+1)=xbestj(t)+F·(xr2j(t)-xr3j(t));r2≠r3

(5)

uij(t+1)=xr1j(t)+F·(xr2j(t)+xr3j(t)-xr4j(t)-xr5j(t));r1≠r2≠r3≠r4≠r5

(6)

2 基于反向學習的跨種群差分進化算法

DE算法在進化過程中，個體間差異性逐漸變小，種群多樣性降低，算法探索能力下降，容易陷入局部最優，出現早熟等問題，為此學者們從不同的角度對算法進行了改進。標準DE算法在尋優過程中的控制參數保持不變，無法較好地滿足進化各階段算法對參數的特殊要求，基于此學者們提出了參數自適應的DE算法；由于初始種群隨機產生，初始解的質量無法保證，因此一些學者對初始化進行了改進；差分策略是DE算法的標志性特征，影響著算法收斂速度和尋優精度，因此學者們提出了多種不同的差分進化策略；DE算法的貪婪選擇策略在提高算法收斂速度的同時降低了種群的多樣性，為避免早熟，學者們改進了選擇策略；考慮到單個種群在進化過程中容易喪失多樣性，學者們提出了多個子種群進化模式，通過種群間的信息共享和交換，保證算法繼續進化。在學習總結學者們的改進策略的基礎之上，本文同時對種群初始化、選擇策略和單種群進化模式等三個方面進行了改進，提出了基于反向學習的跨種群差分進化算法。

2.1 基于混沌分散策略的種群初始化

標準DE算法的初始種群是隨機產生的，用這種方式產生的初始種群，可能會使一些種群個體集中在某一區域或者遠離最優解，無法保證初始解的質量，因此，限制了算法的求解效率。而混沌是非線性動力學系統中特有的一種現象，具有內在的隨機性和遍歷性等特點，它能彌補隨機產生種群的缺點，提高初始種群的質量，為后續的差分操作找到最優解提供了保證。常用的混沌模型是一維Logistic映射[11]，其迭代公式為:

yk+1=μyk(1-yk);k=0,1,…

(7)

其中：k為迭代次數，μ為控制系統混沌行為的參數。當μ值確定后，由任意初值y0∈[0,1],可以迭代出一個確定的時間序列y1,y2, …,yk。當μ=4時，系統沒有穩定解，是[0,1]區間的滿映射，呈現出完全混沌狀態。

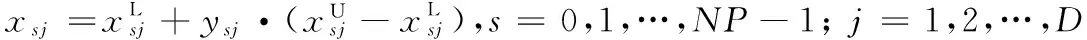
2.2 反向學習精英選擇策略

反向學習策略(Opposition-BasedLearning,OBL)是近年來計算智能領域中出現的一種新技術，已應用到多種優化算法中[12-15]。它的主要思想是：對一個可行解，同時計算并評估其反向解，從中選擇較優的解作為下一代種群。反向學習機制通過搜索更多有效區域來提高群體的多樣性，增強算法的全局搜索能力。本文將其應用在對普通種群的選擇策略上，具體步驟如下：

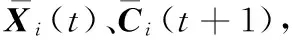
其中:

i=1,2,…,NP-「NP/2?;j=1,2,…,D

將反向學習精英選擇策略用于對普通種群變異交叉后進行選擇操作，能夠有效地提升普通種群進化后的個體的質量，縮小與精英種群個體之間的差距，促進種群之間的交流。反向學習策略通過變換算法的搜索空間，對當前及反向空間進行搜索，使算法避免陷入局部最優，有效提高算法尋優概率[16]。3.3節的實驗結果驗證了該策略的有效性。

2.3 子種群的并行差分進化策略

OLCPDE算法是一種并行的差分進化算法，進化示意圖如圖1所示。該算法根據適應度，將種群劃分2個子種群：精英種群和普通種群。適應度好的前「NP/2?個個體組成精英種群，適應度差的后NP-「NP/2?個個體組成普通種群。對精英種群選用DE/best/1/bin策略進行差分操作，該策略以當前種群最好的個體為基準個體，再加上一個隨機擾動向量，在當前最好的個體周圍進行搜索，具有很好的局部搜索能力。對普通種群選用DE/rand/2/bin策略進行差分操作，該策略在當前種群中隨機選取個體為基準個體，再加上兩個隨機擾動向量進行變異和交叉，選擇操作上采用了反向學習精英選擇策略，不僅擴大了普通種群的搜索范圍，提高了全局搜索能力，而且增加了普通種群產生優質解的概率，有利于種群間的交流。

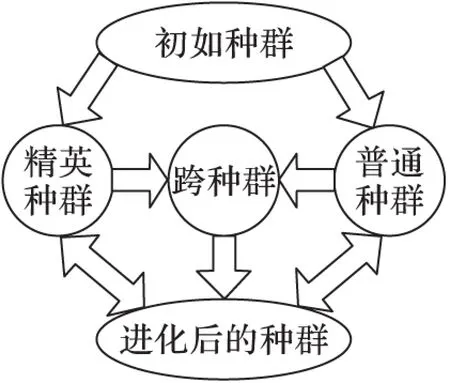
圖1 并行進化示意圖

為了增加算法的魯棒性，提高算法的收斂精度和穩定性，以期能獲得穩定的最優解，本文提出了一種跨種群的DE/best/1/bin策略進行差分進化。該策略生成種群規模為「NP/2?，以精英種群中當前最好的個體為基準個體，隨機選取普通種群中的兩個個體組成擾動向量進行差分進化，在當前最優點的附近進一步搜索，防止了算法的早熟，增加了搜索的精細性。3.3節的實驗結果驗證該策略的有效性。

2.4 算法的實現過程

步驟1 種群初始化。利用混沌分散種群初始化策略產生規模為NP的初始種群，計算個體適應度，并將其按適應度值大小進行排序，選取前「NP/2?個個體組成初始精英種群，剩余NP-「NP/2?個個體組成初始普通種群。

步驟2 對精英種群采用DE/best/1/bin差分策略進行差分進化，得到個體數為「NP/2?的進化后種群。

步驟3 對普通種群采用DE/rand/2/bin差分策略進行變異和交叉，采用2.2節的反向學習精英選擇策略進行選擇，得到個體數為NP-「NP/2?的進化后種群。

步驟4 選取精英種群中的當前最優個體為待變異個體，從普通種群中隨機選擇兩個個體組成擾動向量，采用跨種群的DE/best/1/bin策略進行交叉、變異和選擇，得到個體數為「NP/2?的進化后種群。

步驟5 將三種策略進化后的NP+「NP/2?個個體按適應度值大小排序，選取適應度大的前「NP/2?個個體作為子代精英種群，選取適應度小的后NP-「NP/2?個個體作為子代普通種群。

步驟6 判斷是否滿足算法終止的條件，若當前迭代次數小于最大迭代次數并且沒有尋到最優值則轉向步驟2，否則轉步驟7。

步驟7 結束尋優，輸出結果。

3 函數仿真與分析

3.1 測試函數與參數設置

為了測試OLCPDE算法的性能，本文選取了12個具有不同特點的基準Benchmark函數進行測試，其中f1至f6為單峰函數，f7至f12為多峰函數，測試函數的特征描述如表1所示。

表1 測試函數

選取4種典型算法與OLCPDE算法進行比較，分別是策略為DE/rand/1/bin和DE/rand/2/bin的標準差分進化算法、被廣泛認可的jDE[5]和RMDE[17]。本文選取種群規模NP=80，問題維度n=10。差分進化算法的參數設置主要涉及縮放因子F和交叉概率CR兩個參數，OLCPDE、DE/rand/1/bin、DE/rand/2/bin取F=0.5，CR=0.8；jDE的F和CR是自適應的，參照文獻[5]的設置；RMDE參照文獻[16]的設置F=0.5，CR=0.9，調和參數Mr=0.99。設置f2最大迭代次數設為4 000，f10最大迭代次數為2 000，f11、f12最大迭代次數為1 000，其余的函數最大迭代次數設為300。

3.2 實驗結果及分析

3.2.1 算法收斂的性能

采用上述5種算法對表1中12個測試函數進行尋優，每種算法的每個函數獨立運行30次，尋優結果見表2，收斂曲線如圖2所示(除圖2(g)、(h)、(j)外，其他子圖的縱軸均為對數坐標軸)。

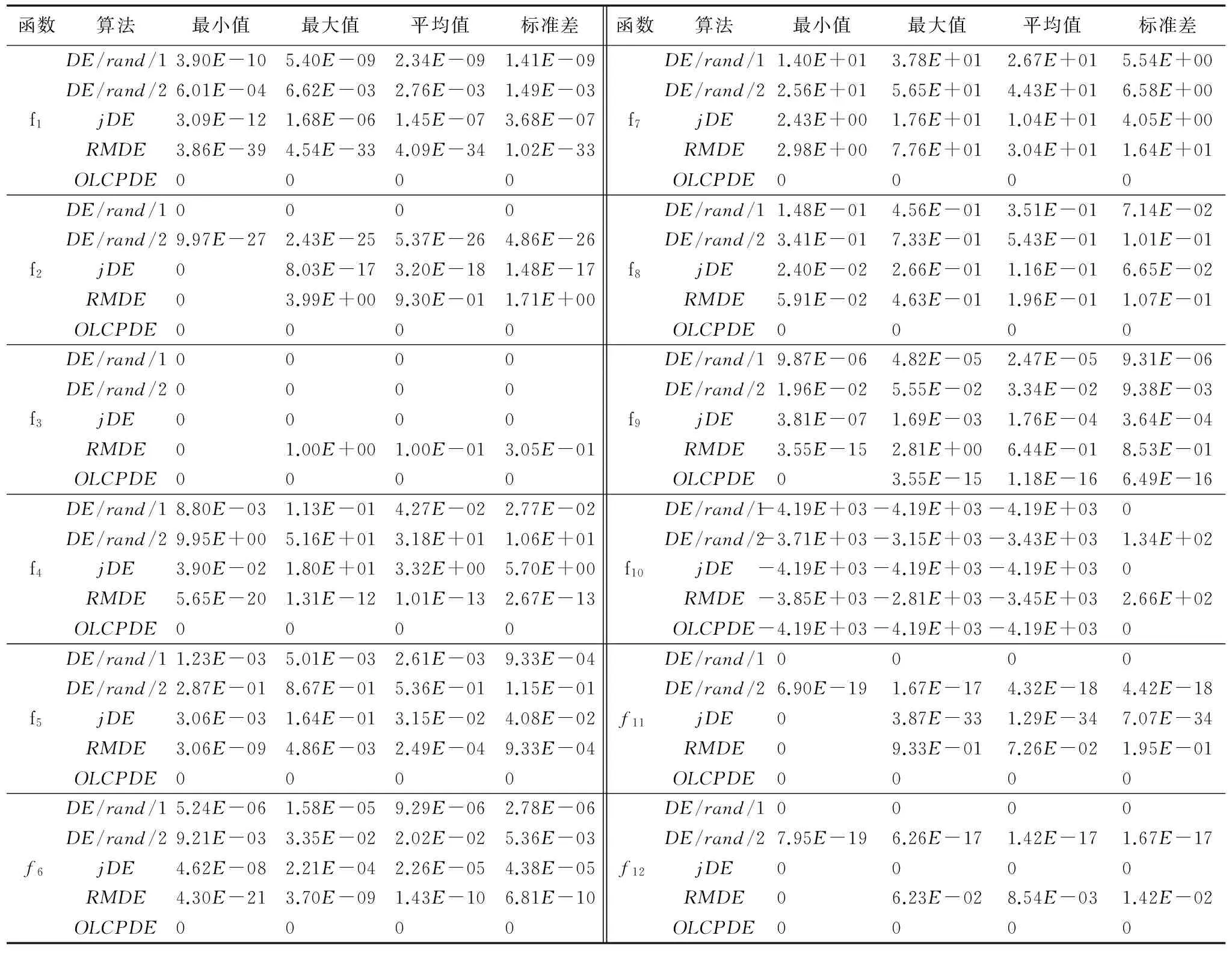
表2 OLCPDE與4種經典算法的收斂性能對比

根據表2和圖2，對算法性能從收斂速度、求解精度以及穩定性等多角度進行對比分析。

對于f1、f4、f5、f6函數，OLCPDE算法在較少的迭代次數下，能夠穩定地收斂到全局最優解，而其他4種算法無論是收斂速度還是求解精度都要差于OLCPDE算法。對于非凸、病態單峰函數f2，OLCPDE算法、DE/rand/1/bin算法、jDE算法和RMDE算法均有可能求解到最優解，但只有前兩種算法最穩定。對于步長函數f6，除RMDE算法，其余四種算法均能穩定求解到全局最優解，其中OLCPDE算法的收斂速度最快。綜合f1～f6函數的求解結果，在求解單峰函數方面，OLCPDE算法具有較快的收斂速度、較強的全局搜索能力和穩定性。

對于f7、f8、f9函數，OLCPDE算法的收斂速度、求解精度和穩定性都要好于其他算法，雖然在對f9函數求解時發生了1次早熟，但求解的精度仍好于其他4種算法；對于f10、f11、f12函數，OLCPDE算法、DE/rand/1/bin算法和jDE算法表現得十分出色，都能穩定地求解到全局最優解，且這三種算法的求解速度差別不大。綜合f7～f12函數的求解結果，求解多峰復雜函數時，OLCPDE算法同樣具有較好的收斂速度、求解精度以及魯棒性。

綜上所述，無論單峰函數或多峰函數，OLCPDE算法均可快速獲取最優值，實驗結果明顯優于其他算法，說明OLCPDE算法具有更好的尋優性能。

3.2.2 算法復雜度分析

由表3可以看出，在最大迭代次數相同的情況下，對于f1～f9函數OLCPDE算法的平均耗時最短，DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法次之，RMDE算法的耗時最長。對于f10～f12函數，OLCPDE函數平均耗時大于DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法，約是它們耗時的1.5倍。分析算法可知，DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法和RMDE算法的時間復雜度相同，均為O(NP*D)，其中RMDE算法的過程更為復雜，所以耗時較多。雖然，OLCPDE算法的時間復雜度為O(3NP*D/2)，但是由于算法的收斂速度較快，在最大迭代次數之內搜索到全局最優點，停止搜索，因此對f1～f9函數搜索的時間消耗小于其他算法。

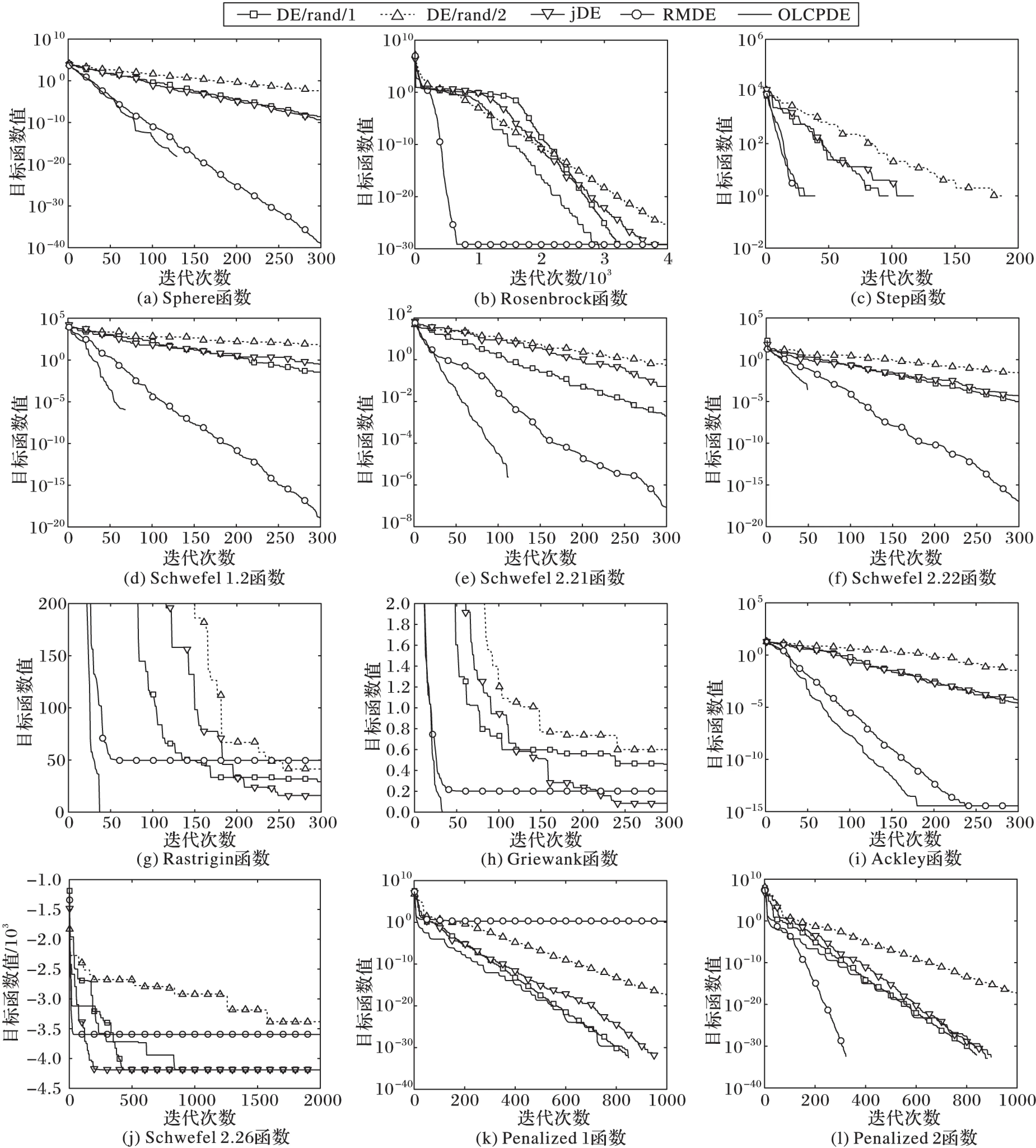
圖2 OLCPDE與4種經典算法的收斂曲線

s

3.3OLCPDE算法策略分析

3.3.1 普通種群選用反向學習精英選擇策略的有效性分析

為了測試反向學習精英選擇策略在算法中的有效性，按照對照實驗的原則，設置3個參照算法，分別是：普通種群使用1對1貪婪選擇的OLCPDE算法(記作CPDE)、精英種群使用了反向學習精英選擇策略的OLCPDE算法(記作EOLCDE)和跨種群策略使用反向學習精英選擇的OLCPDE算法(記作COLCDE)與OLCPDE算法進行比較，參數設置與3.1節相同，尋優結果見表4。

根據表4可以看出，對于上述12種函數，除了f3函數，不使用反向學習精英選擇策略的CPDE算法均無法快速穩定地收斂到全局最優點，說明了使用反向學習精英選擇策略能有效加快算法的收斂；將反向學習精英選擇策略分別用于對精英種群和對跨種群進行選擇的EOLCDE算法和COLCDE算法，能夠尋找到一部分函數的最優值，但是對于其他函數，則容易陷入局部最優。因此，引入反向學習精英選擇策略能夠提高算法的收斂精度和速度，將反向學習精英選擇用作普通種群的選擇策略，才能夠最有效地提升算法的全局尋優能力。

3.3.2 跨種群策略對函數尋優的有效性分析

為了測試跨種群策略在算法中的有效性，設置了取消跨種群策略的OLCPDE算法(記作OLDE)與OLCPDE算法分別對6個單峰函數和6個多峰函數進行對比測試，參數設置與3.1節相同，尋找到最優解的次數統計結果見表5。

根據表5可以看出雖然跨種群策略對多峰函數的尋優的影響性不顯著，但是它能有效提升單峰函數尋優的成功次數，使用跨種群策略的OLCPDE算法能夠防止單峰函數早熟，增加算法的穩定性。

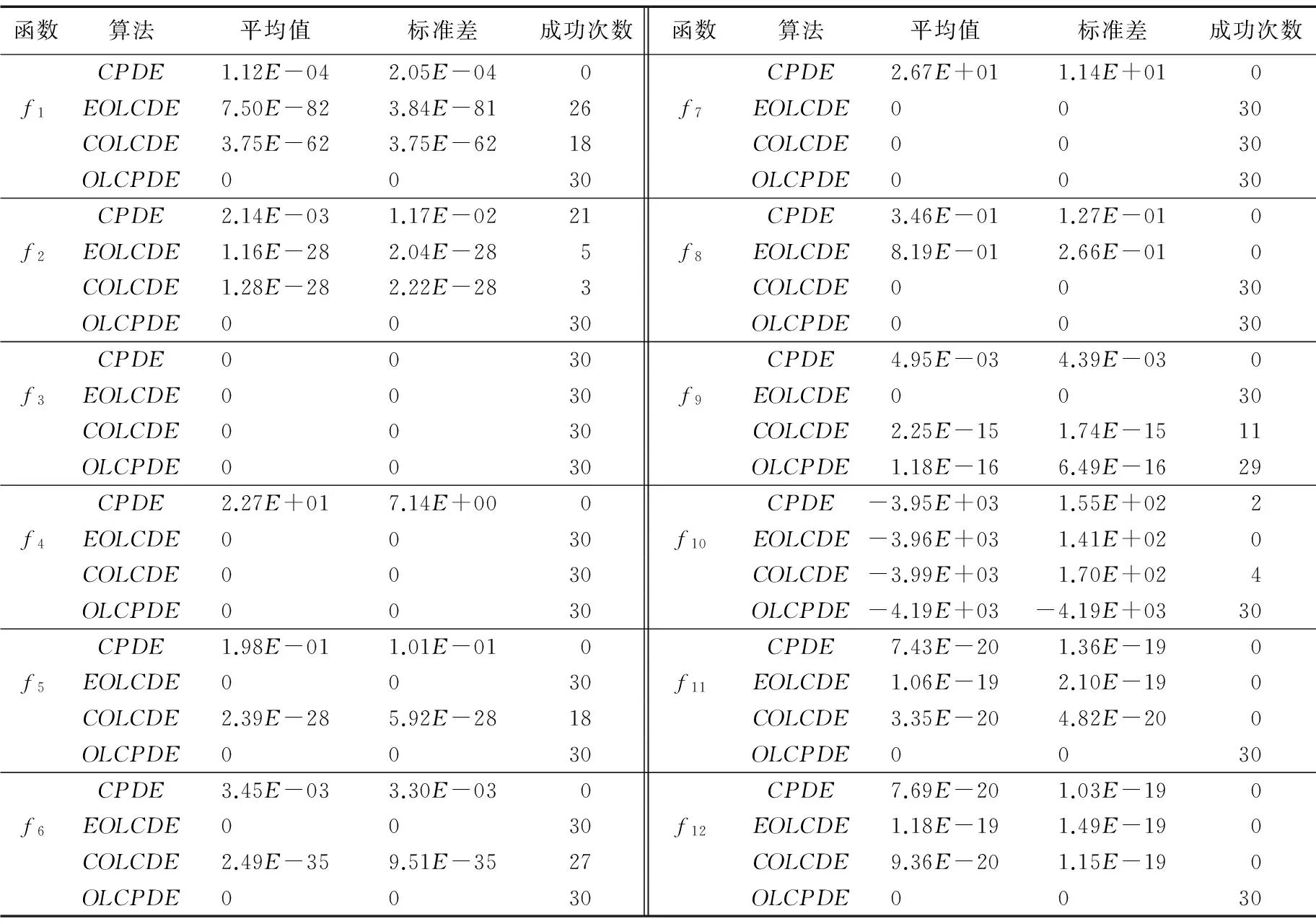
表4 OLCPDE與3個參照算法的收斂性能和尋到最優值的成功次數對比

表5 OLCPDE與OLDE對單峰和多峰函數尋優成功次數比較

3.4OLCPDE算法分析

根據上述圖表可以看出，除個別多峰函數外，OLCPDE算法均能夠穩定地收斂到全局最優解。通過對本文算法策略性能的進行分析，結論如下：

1)通過對反向學習精英選擇策略的性能進行分析，證明該策略有效提升DE算法的尋優精度；同時，將該策略用于普通種群，能最大限度地提高算法的尋優精度，大幅提升尋到最優解的概率。若取消該策略，使用標準DE算法的選擇策略，除個別單峰函數，均無法達到最優解。

2)通過分析跨種群策略對算法的影響，證明運用該策略能有效提升單峰函數尋優成功的次數，進一步提升算法尋優的穩定性。

3)本文算法采用多個子種群進化模式，提高種群多樣性，有效彌補單種群進化過程中種群多樣性不足的缺陷，防止算法早熟。

綜上所述，本文算法策略的使用能有效提升算法性能，無論單峰函數還是多峰函數，OLCPDE算法均能高效、穩定地尋到最優解。

4 結語

針對差分進化算法尋優精度低、收斂速度慢等缺陷，本文提出了一種基于反向學習的跨種群差分進化算法(OLCPDE)，引入混沌分散策略來種群初始化能有效提升初始種群的質量，對普通子種群應用反向學習精英選擇策略，擴大種群的搜索范圍，提升算法的全局搜索能力，采用跨種群的差分進化策略，進一步增強了算法尋優的穩定性。通過對12個標準測試函數的實驗，說明了OLCPDE算法能有效地避免早熟，具有較好的收斂速度、優化精度和魯棒性。將改進的算法應用到實際的工程中，進一步檢驗算法的性能，是下一步將要研究的內容。

)

[1]STORNR,PRICEK.Differentialevolution—asimpleandefficientheuristicforglobaloptimizationovercontinuousspaces[J].JournalofGlobalOptimization, 1997, 11(4): 341-359.

[2]VESTERSTROMJ,THOMSENR.Acomparativestudyofdifferentialevolution,particleswarmoptimization,andevolutionaryalgorithmsonnumericalbenchmarkproblems[C]//Proceedingsofthe2004IEEECongressonEvolutionaryComputation.Piscataway,NJ:IEEE, 2004:267-282.

[3]PRICEK,STORNRM,LAMPINENJA.Differentialevolution:apracticalapproachtoglobaloptimization(naturalcomputingseries) [J].NaturalComputing, 2005, 141(2): 1-24.

[4]VARADARAJANM,SWARUPKS.Networklossminimizationwithvoltagesecurityusingdifferentialevolution[J].ElectricPowerSystemsResearch, 2008, 78(5): 815-823.

[5]BRESTJ,GREINERS,BOSKOVICB,etal.Self-adaptingcontrolparametersindifferentialevolution:acomparativestudyonnumericalbenchmarkproblems[J].IEEETransactionsonEvolutionaryComputation, 2006, 10(6): 646-657.

[6] 汪慎文, 張文生, 秦進, 等.樸素差分進化算法[J]. 計算機應用, 2015, 35(5): 1333-1335.(WANGSW,ZHANGWS,QINJ,etal.Naivedifferentialevolutionalgorithm[J].JournalofComputerApplications, 2015, 35(5): 1333-1335.)

[7] 呂銘晟, 沈洪遠, 李志高, 等.多變異策略差分進化算法的研究與應用[J]. 計算機工程, 2014, 40(12): 146-150.(LYUMS,SHENHY,LIZG,etal.Researchandapplicationofdifferentialevolutionalgorithmundermultiplemutationstrategy[J].ComputerEngineering, 2014, 40(12): 146-150.)

[8] 王叢佼, 王錫淮, 肖建梅.基于極值優化的混合差分進化算法[J]. 計算機科學, 2013, 40(5): 257-260.(WANGCJ,WANGXH,XIAOJM.Hybriddifferentialevolutionaryalgorithmbasedonextremaloptimization[J].ComputerScience, 2013, 40(5): 257-260.)

[9] 匡芳君, 張思揚, 金忠, 等.混沌差分進化粒子群協同優化算法[J]. 微電子學與計算機, 2014, 31(8): 29-33, 39.(KUANGFJ,ZHANGSY,JINZ,etal.Chaoticdifferentialevolutionparticleswarmcooperativeoptimizationalgorithm[J].Microelectronics&Computer, 2014, 31(8): 29-33, 39.)

[10] 張大斌, 楊添柔, 溫梅,等.基于差分進化的魚群算法及其函數優化應用[J]. 計算機工程, 2013, 39(5): 18-22, 27.(ZHANGDB,YANGTR,WENM,etal.Fishwarmalgorithmbasedondifferentialevolutionanditsfunctionoptimizationapplication[J].ComputerEngineering, 2013, 39(5): 18-22, 27.)

[11]OUCM.Designofblockciphersbysimplechaoticfunctions[J].IEEEComputationalIntelligenceMagazine, 2008, 3(2): 54-59.

[12] 周新宇, 吳志健, 王暉.一種精英反向學習的差分演化算法[J]. 小型微型計算機系統, 2013, 34(9):1647-1652.(ZHOUXY,WUZJ,WANGH.Adifferentialevolutionalgorithmusingeliteopposition-basedlearning[J].JournalofChineseComputerSystems, 2013, 34(9): 1647-1652.)

[13]WANGH,WUZ,RAHNAMAYANS.Enhancedopposition-baseddifferentialevolutionforsolvinghigh-dimensionalcontinuousoptimizationproblems[J].SoftComputing, 2011, 15(11): 2127-2140.

[14]WANGH,WUZ,RAHNAMAYANS,etal.Enhancingparticleswarmoptimizationusinggeneralizedopposition-basedlearning[J].InformationSciences, 2011, 181(20): 4699-4714.

[15]AHANDANIMA,ALAVI-RADH.Opposition-basedlearningintheshuffleddifferentialevolutionalgorithm[J].SoftComputing, 2012, 16(8): 1303-1337.

[16] 董小剛, 鄧長壽, 譚毓澄, 等.求解大規模優化問題的正交反向混合差分進化算法[J]. 計算機應用研究, 2016, 33(6): 1656-1661.(DONGXG,DENGCS,TANYC,etal.Hybridizationdifferentialevolutionalgorithmoforthogonalcrossoverandopposition-basedlearningforlarge-scaleoptimizationproblem[J].ApplicationResearchofComputers, 2016, 33(6): 1656-1661.)

[17] 歐陽海濱, 高立群, 孔祥勇.隨機變異差分進化算法[J]. 東北大學學報(自然科學版), 2013, 34(3): 330-334.(OUYANGHB,GAOLQ,KONGXY,Randommutationdifferentialevolutionalgorithm[J].JournalofNortheasternUniversity(NaturalScience), 2013, 34(3): 330-334.)

ThisworkispartiallysupportedbytheNationalNaturalScienceFoundationofChina(71471073, 71171093),theFundamentalResearchFundsfortheCentralUniversities(CCNU14Z02016).

ZHANG Bin, born in 1993, M. S. candidate. His research interests include logistics system optimization, intelligent optimization.

LI Yanhui, born in 1974, Ph. D., professor. His research interests include logistics and supply chain management, management information system.

GUO Hao, born 1987, Ph. D. candidate. His research interests include logistics system optimization.

Cross-population differential evolution algorithm based on opposition-based learning

ZHANG Bin, LI Yanhui, GUO Hao*

(School of Information Management, Central China Normal University, Wuhan Hubei 430079, China)

Aiming at the deficiencies of traditional Differential Evolution (DE) algorithm, low optimization accuracy and low convergence speed, a Cross-Population Differential Evolution algorithm based on Opposition-based Learning (OLCPDE) was proposed by using chaos dispersion strategy, opposition-based optimization strategy and multigroup parallel mechanism. The chaos dispersion strategy was used to generate the initial population, then the population was divided into sub-groups of the elite and the general, and a standard differential evolution strategy and a differential evolution strategy of Opposition-Based Learning (OBL) were applied to the two sub-groups respectively. Meanwhile, a cross-population differential evolution strategy was applied to further improve the accuracy and enhance population diversity for unimodal function. The sub-groups were handled through these three strategies to achieve co-evolution. After the experiments are totally run for 30 times independently, it is proven that the proposed algorithm can stably converge to the global optimal solution in 11 functions among 12 standard test functions, which is superior to other comparison algorithms. The results indicate that the proposed algorithm not only has high convergence precision but also effectively avoid trapping in local optimum.

Differential Evolution (DE); Opposition-Based Learning (OBL); cross-population; chaos search; function optimization

2016- 08- 02;

2016- 09- 28。

國家自然科學基金資助項目(71471073,71171093);中央高校基本科研業務費專項資金資助項目(CCNU14Z02016)。

張斌(1993—),男,湖北襄陽人,碩士研究生,主要研究方向：物流系統優化、智能計算; 李延暉(1974—),男,湖南衡陽人,教授,博士,主要研究方向：物流與供應鏈管理、管理信息系統; 郭昊(1987—),男,湖北荊州人,博士研究生,主要研究方向：物流系統優化。

1001- 9081(2017)04- 1093- 07

10.11772/j.issn.1001- 9081.2017.04.1093

TP301.6;TP18

A