均質黏土滑坡的運動特性研究
儲 浩,孫樹林,2,張 磊,丁 偉
均質黏土滑坡的運動特性研究
儲 浩1,孫樹林1,2,張 磊1,丁 偉1
(1.河海大學 地球科學與工程學院,江蘇 南京 211100;2.河海大學 水文水資源與水利工程科學國家重點實驗室,江蘇 南京 210098)
為研究均質黏土滑坡的運動特性,根據黏土滑坡特性定義圓弧形滑動面為最危險滑移面,基于質心法的運動假設,建立失穩后滑坡的物理運動模型,依據滑坡運動過程中功能轉換關系,推導出滑坡滑動距離的預測公式,通過計算獲取其運動加速度、速度、滑動距離等動力學參數,并將該方法計算得到的結果與雪橇模型結果對比。結果表明:均質黏土滑坡運動加速度在極短的時間內達到最大,而后逐漸降低;滑坡的運動速度在最初階段增加較快,此后逐漸減小直至滑坡停止;該方法得到的最終水平滑動距離與雪橇模型計算結果基本一致,相對誤差較小,僅為1.2 %。關鍵詞:滑坡;均質黏土滑坡;圓弧滑動;能量守恒
滑坡是一種常見的地質災害,中國是亞洲乃至世界上滑坡災害最為嚴重的地區之一,嚴重的滑坡災害不僅給當地居民的生命財產造成極大損失,也嚴重影響鐵路、公路、水運及水電站等基礎設施的安全運營[1-3]。在滑坡穩定性分析研究方面,國內外學者做了大量研究工作,形成諸多科學分析理論和方法[4-6]。但由于滑坡災變的復雜性、作用因素的隨機性、可變性和不確定性[7],滑坡失穩后的運動特征研究廣受限制,滑坡預測的研究尚存諸多問題。許多學者基于滑坡體質心運動和能量轉換的方法對失穩后滑坡的運動規律展開研究[8-10]。然而這些研究并未深入考慮每一微小時間段內滑坡功能轉換關系,也忽略了對某一不確定階段滑面坡角的準確計算,故其只能應用于滑坡運動的整體過程的分析。對于滑坡防災減災工作,預測潛在滑坡的危害范圍是亟待解決的關鍵性問題,準確快捷地計算滑坡體每一運動階段的速度和滑動距離對于災害評估與規避具有重要意義。為此,本文以均質黏土滑坡為研究對象,選取圓弧形滑動面為最危險滑移面,基于質心法的運動假設,建立失穩后滑坡的物理運動模型,從而進行黏土滑坡的運動速度、滑動距離的預測,為滑坡災害的危險評估和科學減災提供理論支持。
1 滑坡運動物理模型的建立
Heim于1932年提出“雪橇模型”來解釋滑坡運動過程中的功能轉換關系,該模型基于能量線的概念來計算滑坡速度和滑動距離[11]。雪橇模型簡單合理,但只是粗略地考慮滑坡體整個滑動過程中的能量守恒,并未對每一微小階段間的功能轉換情況深入研究。本文建立的運動模型在“雪橇模型”的基礎上,考慮圓弧形滑動面上的質心運動方程,對每一微小滑動階段進行功能轉換關系分析。將每一階段的滑動距離進行疊加,直至滑坡運動停止,最終得到均質黏土滑坡的滑動總距離。
考慮二維平面問題,對潛在的黏土滑坡進行穩定性分析,確定其最危險滑移面分布。圖1所示為運動分析的雪橇模型,假定滑坡運動期間所有的能量損失均起因于摩擦做功,能量線代表著滑坡運動過程的動能與勢能之和,動能由能量線與運動塊體重心間的高差表示。
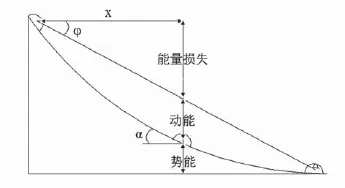
圖1 滑坡運動的雪橇模型Fig.1 Sled model of landslide
根據極限平衡原理,建立公式:
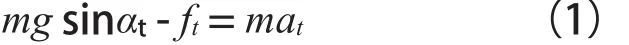
式中,at為t時刻滑坡體的運動加速度;αt為t時刻滑坡質心所在圓弧面的切線坡角;?t為t時刻的摩擦力,由公式(2)所確定。
滑坡體沿著滑動面運動,其與滑動面之間的滑動摩擦力為:
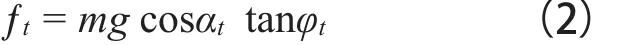
式中,φt為滑坡體與滑動面之間的動摩擦角,假定滑坡體在任意時刻與滑動面間的動摩擦角不變,即都為φ。
對滑坡在t~t+Δt時段分析,t時刻速度為vt,加速度at可由(1)式計算,即:
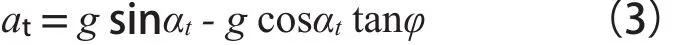
當時間間隔Δt很小,則可以事先假設在t~t+Δt時段內,滑坡的運動加速度不變,即t+Δt時刻滑坡體的速度為:

t~t+Δt時段內,滑坡運動過程的勢能變化為:

同時因摩擦力做功造成的能量損失表達式如下:
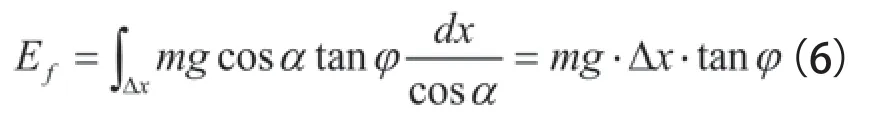
根據t~t+Δt時段內,滑坡運動過程能量守恒,即:
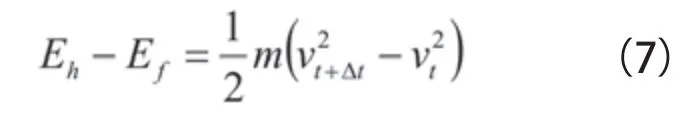
將(5)式和(6)式代入(7)式中,可求出Δx,即:
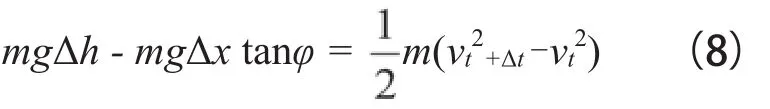
圖2展示了t~t+Δt時段內質點在圓弧面上運動的幾何關系,O為圓弧的圓心,B點為t時刻質點所在的位置,C點為t+Δt時刻質點所在的位置,BE長為Δx,EC長為Δh。
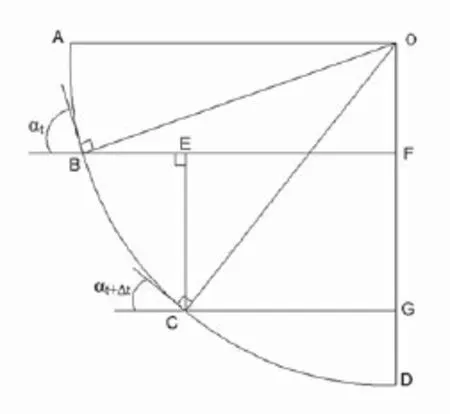
圖2 t~t+Δt時段內質點運動幾何關系圖Fig.2 Geometric diagram of mass point in t~t+Δt
由圖2可得:
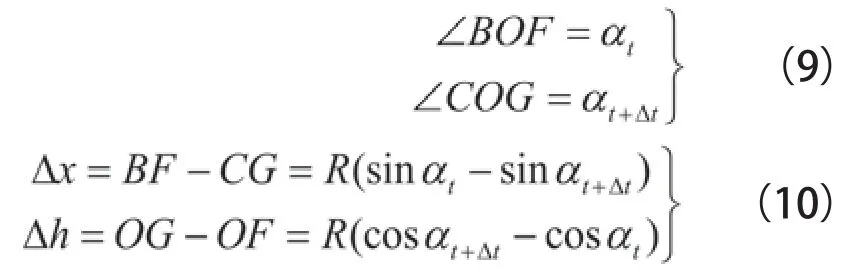
整理(10)式,可得Δh與Δx關系如下:
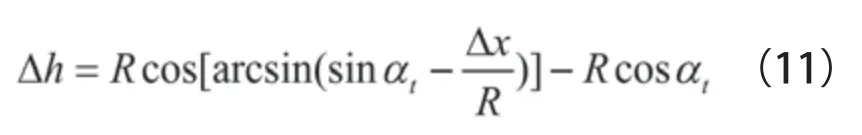
將(4)式與(11)式代入(8)式,即可求出t~t+Δt時段內滑坡滑移的水平距離Δx和垂直距離Δh。
得到水平距離Δx之后,t+Δt時刻圓弧面切線坡角可由下式求得:
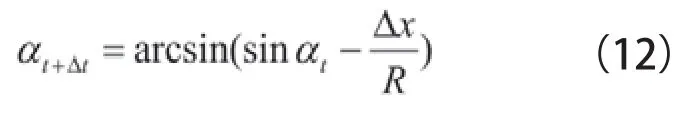
同時,由圖2幾何關系可知,圓弧面切線坡角的變化與圓心角的變化同步,即在t~t+Δt時段內,圓心角的變化關系如下式:
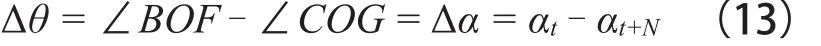
進而,t~t+Δt時段內,滑坡運動的弧長,即滑距為:
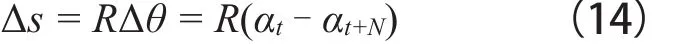
以上表達式可以計算一個時間步長Δt內滑坡運動的速度、滑動距離等動力學參數,并且由(12)式可計算出t+Δt時刻滑坡體所在位置的圓弧面切線坡角,從而進入下一個時間步的計算,依據(1)式確定出下一時間步的加速度。當αt等于0時,可以計算滑坡體滑出圓弧滑面時的速度。以此計算,直到滑坡體速度為0,則運動停止,每一時間步的Δs累計相加,即為該滑坡運動總的滑距。
2 案例分析
2.1 滑坡模型
以某高速公路旁黏土滑坡為例,圖3為該邊坡滑移面示意圖。A-B-C-D-A為滑坡體,A-D-C為最危險滑移面,C-E為邊坡旁高速公路。假定土質均勻,最危險圓弧形滑移面半徑為R=100 m,土體容重γ =17.5 kN/m3,內聚力c =63 kPa,假定滑動摩擦角φ=21?,運動加速度取g =9.8 m/s2。
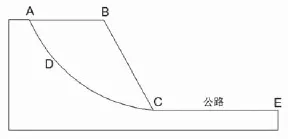
圖3 邊坡滑移面示意圖Fig.3 Slip surface of slope
2.2 計算分析
滑坡啟動時刻滑坡體質心底面與水平面的夾角α0=76?,應用所建立的物理運動模型,對該黏土滑坡運動分析,計算出該滑坡的最大運動速度和運動距離,計算結果見圖4和圖5。
由圖4可知:黏土滑坡運動加速度在極短時間內達到最大,加速度最大值為9.527 m/s2,此后依次減小,在大約4.5 s時加速度下降至0,之后呈負增長。說明4.5 s左右滑坡由加速階段轉至減速階段,相對于加速階段而言,該減速階段滑坡體因克服摩擦阻力而消耗的能量大于重力勢能降低轉化的能量。從圖5可以看出:滑坡運動速度呈現先增大后減小的趨勢,滑坡體運動速度增長較快,在極短時間內達到最大速度,此后運動速度開始減小直至運動停止,其中速度最大值為30.214 m/s。
同時,滑坡體在6.5~7.0 s時間段到達圓弧滑動面的最低點,在最低點的速度為27.825 m/s,此后沿水平路面滑動,根據運動學公式計算出該階段滑坡體滑行102.905 m后停止。累計每一時間段滑坡體的水平位移,可以得出最終滑坡體最大水平位移約199.893 m。
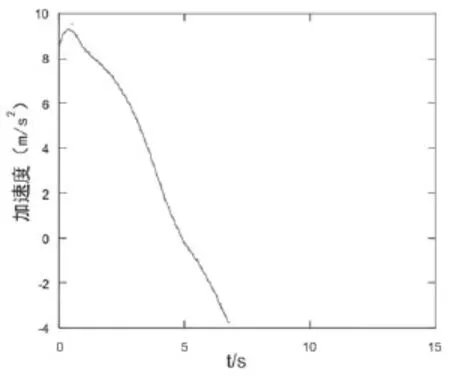
圖4 滑坡加速度與運動時間關系圖Fig.4 Relationship between the accelerated velocity and time
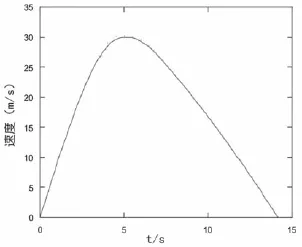
圖5 滑坡速度與運動時間關 系圖Fig.5 Relationship between the velocity and time
2.3 結果對比
應用Heim雪橇模型計算該案例,對比二者結果,對所提方法的準確性進行分析。
根據上述案例條件,可知滑坡體失穩前后質心的高度差為:
H = 100 - 100sin76°/tan76°=75.808 m (15)
將前后高度差H及案例參數代入Heim雪橇模型計算公式中,計算得到最終的水平位移為197.486 m。本文所提模型的計算結果相對于雪橇模型得出的結果的絕對誤差為2.407 m,相對誤差為1.2 %,相對誤差較小,證明本文所建模型可行性和合理性。
3 結論
1)以黏土滑坡運動為研究對象,以圓弧面為最危險滑移面,在雪橇模型的基礎上對每一微小滑動階段進行功能轉換關系分析,建立黏土滑坡的物理運動模型,提出均質黏土滑坡運動特性研究的一種新方法。
2)黏土滑坡的運動加速度在啟動時刻極短時間內達到最大,而后依次減緩,在某一時刻減至0后滑坡體呈減速運動;滑坡體速度總體呈現先增大后減小的趨勢,直至速度為0則滑坡體停止運動。同時對比雪橇模型的計算結果,二者相對誤差僅為1.2 %,證明了所述方法對于均質黏土滑坡運動參數的計算是可行的。
3)應用所述方法能夠計算黏土滑坡體在圓弧滑面上最低點的運動速度,進而可計算出該點處滑坡體動量等物理量,為抗滑樁、擋土墻等工程提供數據支持。
[1]黃潤秋. 20世紀以來中國的大型滑坡及其發生機制[J]. 巖石力學與工程學報,2007,26(3):433-454.
[2]王思敬. 工程地質學的任務與未來[J]. 工程地質學報,1999(3):195-199.
[3]張倬元. 滑坡防治工程的現狀與發展展望[J]. 地質災害與環境保護,2000,11 (2):89-97.
[4]李世海,劉天蘋,劉曉宇,等. 論滑坡穩定性分析方法[J]. 巖石力學與工程學報,2009,28(Z):3309-3334.
[5]孫樹林,秦鮮瑋,朱明杰,等. 均質土坡穩定性分析的圖解法研究[J]. 科學技術與工程,2015,15(8):214-218.
[6]毛 碩,王運生. 雅礱江中游某滑坡形成機制及穩定分析[J].河北工程大學學報:自然科學版,2016,33(1):91-95.
[7]王念秦,王永鋒,羅東海,等. 中國滑坡預測預報研究綜述[J]. 地質評論,2008,54(3):355-361.
[8]王家鼎,黃海國,阮愛國,等. 滑坡體滑動軌跡的研究[J]. 地質災害與防治,1991,2 (2):1-10.
[9]谷天峰,王家鼎,梁 輝,等. 均質土體滑坡運動規律分析[J]. 西北大學學報:自然科學版,2006,36 (3):437-441.
[10]董孝壁,王蘭生. 斜坡破壞后滑體的運動學研究[J]. 地質災害與環境保護,2000,11(1):31-37.
[11]HEIM A. Bergsturz and Menschenleben[M]. Zutich:Naturfor-schenden Geology,1932:218.
(責任編輯 王利君)
Study on the motion characteristic of clay landslide
CHU Hao1,SUN Shulin1,2,ZHANG Lei1,DING Wei1
(1.School of Earth Science and Engineering, Hohai University, Jiangsu Nanjing, 211100; 2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Jiangsu Nanjing, 210098)
In order to analyze the motion characteristic of clay landslide, the circular sliding surface is defined as the most dangerous slip plane according to clay landslide characteristic. Base on the assumption that landslide moves as a group of particles motion, the physical motion model of landslide failure is established. Base on function transformation relations, in the process of landslide movement the forecast formula of landslide distance is deduced. Kinetic parameters such as motion acceleration velocity, sliding distance are obtained by calculation. Compared with the sled model, this method can be used for landslide case. The case results show that the motion acceleration of homogeneous clay landslide approaches to its maximum immediately in a very short time, and then reduces gradually. Landslide movement speed increases rapidly in the initial stage, then slows down gradually until the landslide movement stops. The final horizontal sliding distance of this method is equal to the result calculated by the sled model approximately, and the relative error is only 1.2 %, which is very small.
landslide; homogeneous clay landslide; sliding along circular surface; energy conservation
P642.22
A
1673-9469(2017)02-0070-04
10.3969/j.issn.1673-9469.2017.02.014
2017-04-10
國家重點實驗室開放研究基金資助項目(2005408911);留學回國人員科研基金資助項目(20071108);江蘇省環境保護廳項目(201029)
儲浩(1993-),男,安徽安慶人,碩士,從事地質環境保護與地質災害防治方面的研究工作。

