關于一道北京大學自主招生(2009年)試題的探討
孫望濤 胡曉雄
(浙江省長興中學,浙江 湖州 313100)
?
關于一道北京大學自主招生(2009年)試題的探討
孫望濤 胡曉雄
(浙江省長興中學,浙江 湖州 313100)
1 問題的提出
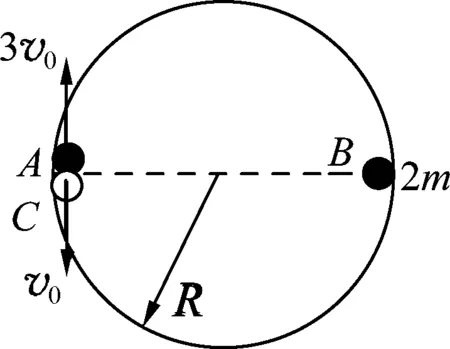
圖1
原題.(2009年北大自主招生試題)如圖1所示,光滑的水平桌面上平放著一個半徑為R,內壁光滑的固定圓環,質量分別為m、2m、m的小球A、B、C在圓環內側的位置和速度大小、方向均在圖中標出,初始B小球靜止,已知所有碰撞為彈性碰撞,試問,經過多長時間,A、B、C3個小球又第1次恢復到原來位置.
此題也出現在文獻[1]中,試題和文獻[1]中給出的參考答案如下.
參考答案:首先推導兩個物體發生彈性碰撞后的通解公式.由系統動量守恒定律得
m1v10+m2v20=m1v1+m2v2,
由碰撞前后動能之和保持不變,有
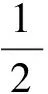
聯立解得
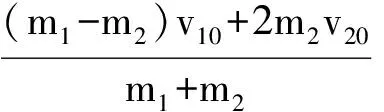
(1)
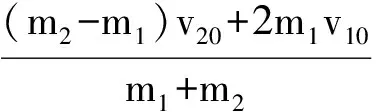
(2)
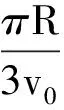
②B與C經歷時間t2后發生碰撞,B、C碰后速度通過公式(1)、(2)計算得vB2=v0,vC2=-3v0.
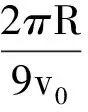
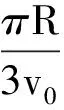
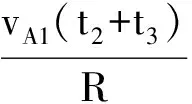
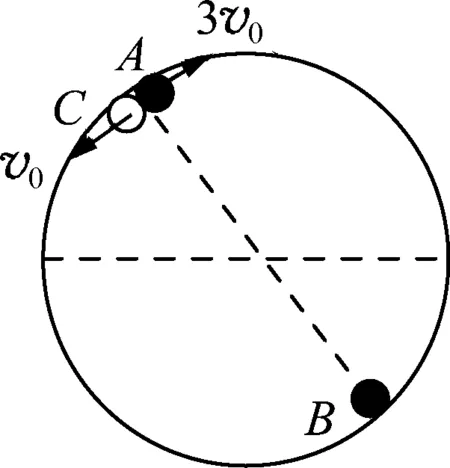
圖2
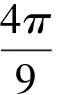
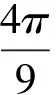
上述解答中每一次碰撞都需將兩小球質量、碰前速度代入碰撞通解公式(1)、(2)進行運算,計算量較大,十分繁瑣.
2 轉換參考系簡化解題過程
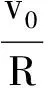
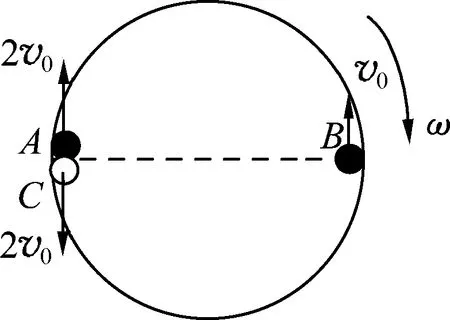
圖3
在此參考系中,vA=2v0,vB=-v0,vC=-2v0,我們驚訝地發現,PA=2mv0,PB=2m(-v0)=-2mv0,PC=m(-2v0)=-2mv0,即A、B、C3小球動量大小相等.我們知道,當兩個動量大小相等,方向相反的小球發生對心彈性碰撞時,小球碰后反向運動,且速度大小與原速度相等.
于是,本題變得異常簡單,我們記碰撞發生的位置相對于A、C起點轉過θ.
①A與B相碰.如圖4所示,有
②B與C相碰.如圖5所示,有
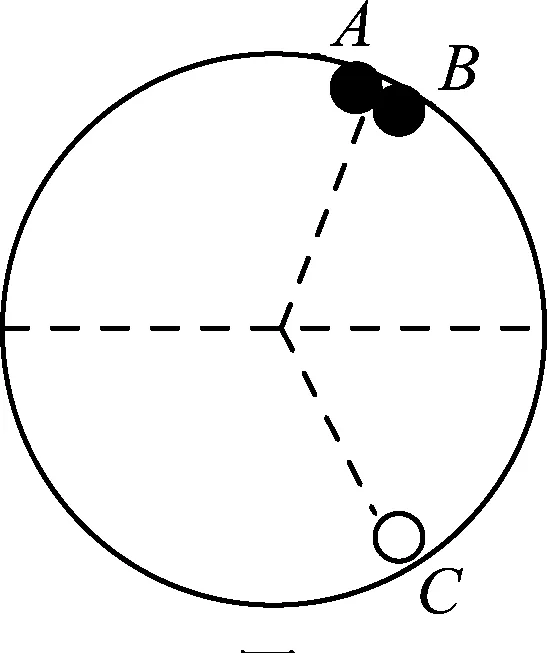
圖4
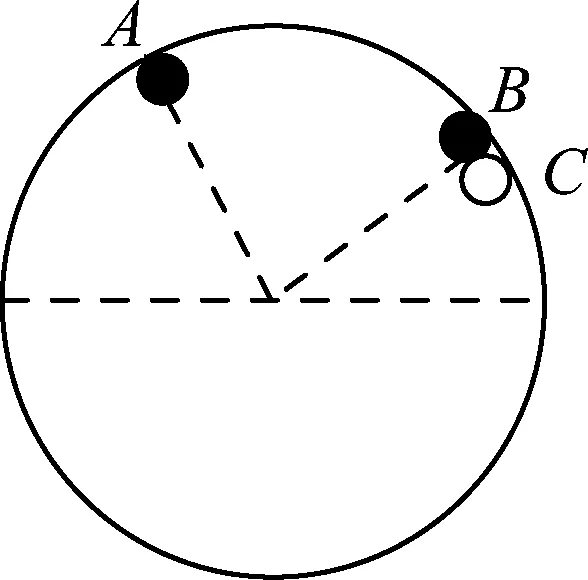
圖5

圖6
③C與A相碰.如圖6所示,有
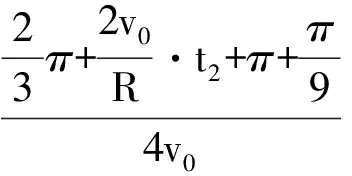
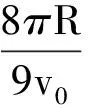
3 關于問題的進一步探討

圖7
我們再來探討3球在動量相等的前提下需滿足何種條件才能使運動具有周期性.如圖7所示,設3小球速率為v1、v2、v3(已滿足p1=p2=p3),用θ表示相碰兩球相對x軸順時針轉過的角度,θ′表示兩球相碰時第3球相對x軸順時針轉過的角度,以下省略大量計算過程.
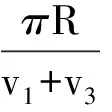
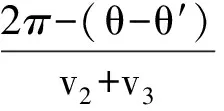
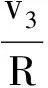
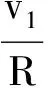
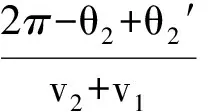
要使3球相對位置回到初態,則θ3=θ3′+π,解得v1=v2.
由此得出結論:如圖8所示,任意3個動量大小相等的小球在圓環內發生碰撞,只要初態A、C兩球速度大小相等,方向相反,它們的運動具有周期性.
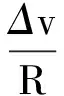

圖8 圖9
1 江四喜.重點大學自主招生物理培訓講義[M].第3版.合肥:中國科學技術大學出版社,2016:92-93.
2 胡曉雄.對教輔中一道結構不良習題的分析與反思[J].物理通報,2015(6):45-46.
2017-01-21)

