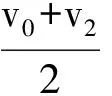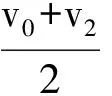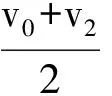例談物理解題中似是而非的“平均值”

彭立君

(湖南省岳陽市第一中學，湖南 岳陽 414000)

?

例談物理解題中似是而非的“平均值”

彭立君

(湖南省岳陽市第一中學，湖南 岳陽 414000)

本文通過解析兩例采用平均值求解物理問題的過程,分析說明平均值求解問題的非一般性,當命題中的物理量處于變化狀態時應采用微元分析，化變化量為不變量進行處理求解．

平均值； 均勻變化； 非一般性； 微元分析

當量值處于變化狀態時,“平均值”是一種習慣的思維方式．當物理量處于均勻變化時,采用平均值處理問題也是物理解題中的一種常用方法．同樣,命題者在命題時也往往在問題情景中設置均勻變化的物理量,促成解題時能夠使用平均值處理．但是平均值求解并非十分嚴謹的科學方法,有時簡單采用平均值處理可能會得到正確的答案,卻不一定正確理解了物理情景,有時不經深思采用平均值進行問題的求解,則會造成問題的錯解．下面,從兩例問題來思考如何正確看待物理解題中的“平均值”．

1 “平均值”帶來的解題失誤

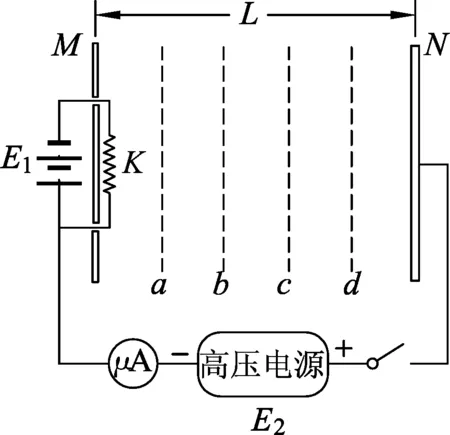
圖1

例1.當金屬的溫度升高到一定程度時就會向四周發射電子,這種電子叫熱電子,通常情況下,熱電子的初始速度可以忽略不計．如圖1所示,相距為L的兩塊平行金屬板M、N接在輸出電壓恒為U的高壓電源E2上,M、N之間的電場近似為勻強電場,a、b、c、d是勻強電場中4個均勻分布的等勢面,K是與M板距離很近的燈絲,電源E1給K加熱從而產生熱電子．電源接通后,電流表的示數穩定為I,已知電子的質量為m、電荷量為e．求:

(1) 電子達到N板瞬間的速度;

(2) 電子從燈絲K出發達到N板所經歷的時間;

(3) 電路穩定的某時刻,M、N之間運動的熱電子的總動能．

本例題流轉于網絡、復習資料,甚至出現在大型考試中,無論是網絡、復習資料還是考試中的參考答案一律采用平均值求解,恰恰本例雖是一種均勻變化，卻不能采用平均值求解．

參考答案(第3問為典型錯解):

(1) 電場中加速,由動能定理得

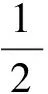
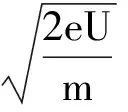
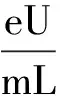
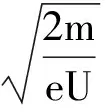
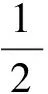
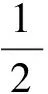
有沒有更讓人信服的方法求解呢?

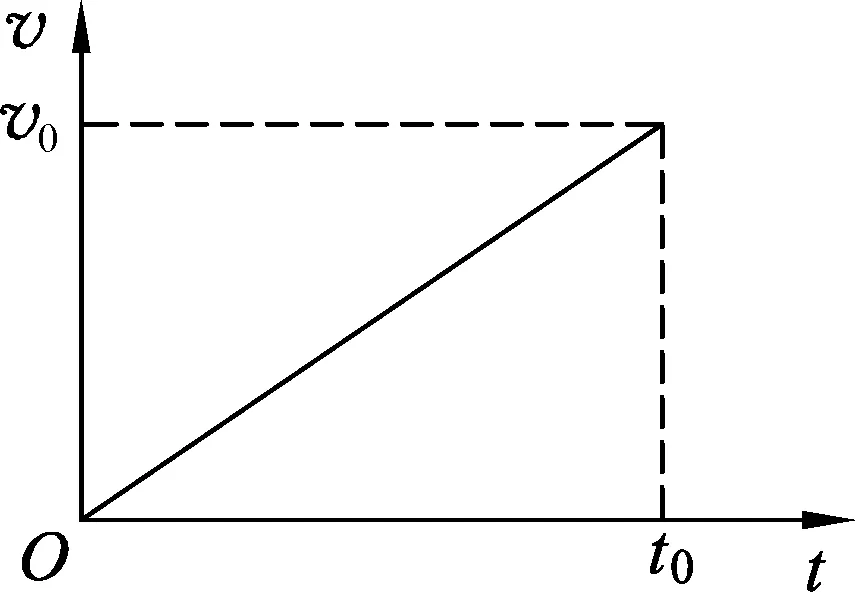
圖2

不妨作出t0時間內的帶電粒子的v-t圖像,如圖2所示．設t0為帶電粒子在電場中運動的時間,則v0為帶電粒子到達右極板時的速度．同樣也可以把圖像看作是極板間所有粒子速度隨時間的分布．由于電流穩定為I,在相等時間間隔內通過截面的電荷量相等,故圖中取相等的時間間隔分析,其對應的電荷數相等．

設板間電荷總量為Q,則Q=It．

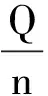
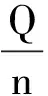
板間粒子總動能為

Ek總=∑Eki，

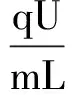
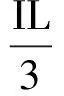
本例也可以直接從電場力做功等于動能的增量的角度來處理．

設板間電荷總量為Q,把電荷量按時間順序均分為n等份，第n等份恰好到達N板,有

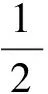
則第i等份到達的位置距離M板為

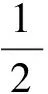
由動能定理知,第i等份電荷量所具有的動能為

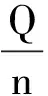
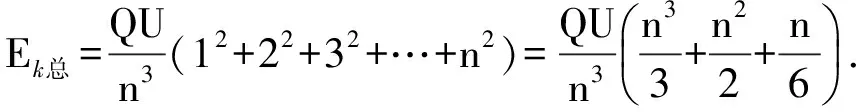
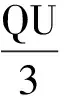
2 “平均值”似是而非的巧合

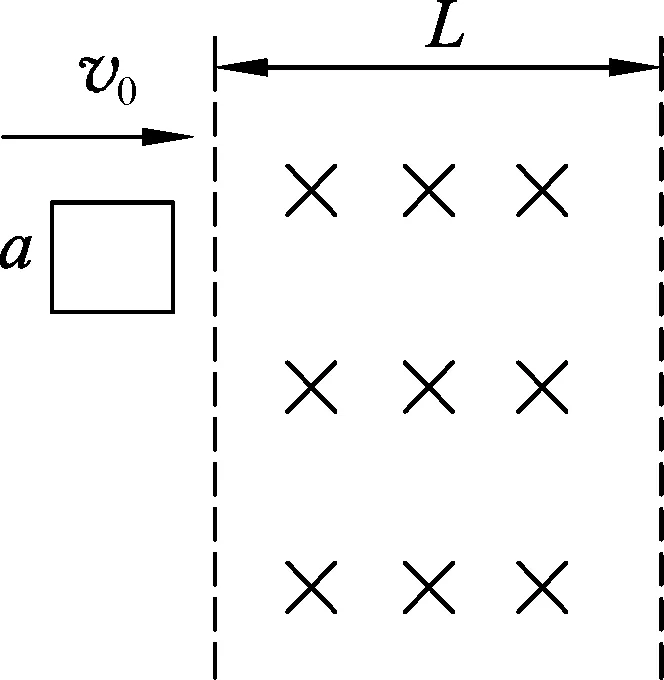
圖3

例2.一有界勻強磁場區域的寬度為L,磁場方向豎直向下,在光滑的水平面上,一個邊長為a(a

本例題也是常見于各種復習資料、網絡中,看似一種不均勻變化,但又似乎能用平均值進行處理．最簡單的想法,當然是相加除2．這是沒有情景思考的一個想法,也巧合了本題的答案．

本題常采用動量定理求解．

對線框進入磁場過程分析,由動量定理可知

對線框穿出磁場過程分析,由動量定理可知

任取很短的一段時間Δti分析,由于時間很短電流可以看作不變量．

兩邊同乘以Δti，得

則這段時間內流過導線截面得電荷量為

由此可知

從以上兩例的解析過程可知,“平均值”未經嚴謹的推理驗證,并不能只根據想象就可以采用,它不是一種十分嚴謹的科學方法,是一種經驗后的非一般性處理問題方法．當處理物理量發生變化的問題時,若未經嚴謹的邏輯推理,不應該采用“平均值”的方式處理,應采用微元分析把變量轉換為不變量進行問題的分析．

本文系湖南省教育規劃課題“數學模型在中學物理教學中的建構與應用研究”(批準號： XJK014CZXX077)的階段性成果.

2017-02-12)