基于高頻數據的統計套利組合策略研究

周明華，周婷婷，張敏凱

(1.浙江工業大學 健行學院，浙江 杭州 310023；2.浙江工業大學 理學院，浙江 杭州 310023)

基于高頻數據的統計套利組合策略研究

周明華1，周婷婷2，張敏凱2

(1.浙江工業大學 健行學院，浙江 杭州 310023；2.浙江工業大學 理學院，浙江 杭州 310023)

采用滬深300股指期貨當月連續合約與次月連續合約的1min高頻數據，借鑒組合思想，引入伯努利隨機變量，將GARCH(廣義自回歸條件異方差模型)模型與Ornstein-Uhlenbeck模型進行組合，設計出新的統計套利組合策略，并在改進的統計套利策略的基礎上進行套利.我們采用動態交易的方式對改進后的交易策略的實際交易效果和模型的有效性進行檢驗，實證檢驗結果表明：對單一套利模型進行組合是必要的，組合后的整體套利收益水平相較單一模型套利收益來說明顯提高了.

高頻數據；GARCH；Ornstein-Uhlenbeck；組合策略；伯努利變量

目前，國內外針對統計套利的很多研究是結合一些人工智能方法與統計套利模型.Nikos等[1-2]將神經網絡算法與GARCH模型結合設計了一個新的統計套利模型.Triantafyllopoulos等[3]將時變狀態空間模型、貝葉斯方法兩者組合，構建了時變貝葉斯自回歸模型來模擬了價差的均值回復過程.伍娟[4]，楊懷東[5]將卡爾曼濾波模型、協整模型相結合，提出新的統計套利模型來解決協整系數的時變性問題.王紅麗[6]基于對單一波動預測模型的優勢和不足進行比較分析，同時考慮時變性情況，對單一模型配置變權重，構建提出了時變組合預測模型，并將其應用于滬深300股指期貨波動的預測中，取得了較好的擬合和預測效果.張福余[7]將傳統協整模型和狀態空間模型結合，來達到時變參數的要求，并利用卡爾曼濾波算法估計參數，然后用時變的協整模型來擬合價差序列，尋找套利機會.雖然國內外一些學者也利用了組合思想，將一些人工智能算法引入到統計套利模型中，但很少有學者對單一統計套利模型的組合方法進行研究.

針對某一問題，從不同的角度和建模方式考慮，可以有不一樣的預測方法.但單一套利模型并不在每一時段都有最優的預測效果.為此，選取了幾種套利模型，對期貨的當月合約和次月合約在2014年到2015年的1 min高頻數據進行驗證分析，發現各模型在各個時間段套利的套利次數、套利成功次數、累積收益率、平均單次收益率等都不存在一致變動現象，套利結果在某一時段效果好，另一時段效果并不一定好.因此可以考慮各模型的優點，將模型組合進行套利.在這里選取基于GARCH的統計套利方法和基于Ornstein-Uhlenbeck的統計套利方法，利用伯努利隨機變量，將兩種模型策略有效組合起來，然后在改進的統計套利策略的基礎上進行套利，并與僅使用基于GARCH模型的套利結果和僅使用基于Ornstein-Uhlenbeck模型的套利結果相比較，發現采用組合策略進行統計套利時，其累計收益率均大于采取單一模型進行套利時的累計收益率，達到了增加收益的目的，表明組合策略是有效的.

1 統計套利模型

1.1 價差序列的計算

選取滬深300股指期貨合約的當月合約IFL0和次月合約IFL1，設兩合約在t時刻的價格分別為Ft和FT，則價差為

spreadt=FT-Ft

(1)

為了更方便地查看價差波動情況，對價差序列去中心化操作(價差與價差平均值的差)，所得殘差序列為

Mspreadt=spreadt-mean(spreadt)

(2)

1.2 基于GARCH模型

對每一期的滬深300股指期貨去中心化殘差序列Mspreadt進行自相關和偏相關分析，得出Mspreadt～AR(p1)，即

Mspreadt=α1Mspreadt-1+α2Mspreadt-2+…+αp1Mspreadt-p1+residualt

(3)

再建立條件異方差函數為

residualt～σtet

(4)

ω>0,ηi≥0,λj≥0

式中et～N(0,1).

由式(3)可知：下一期的殘差residualt+l為

residualt+l=Mspreadt+l-α1Mspreadt+l-1-α2Mspreadt+l-2-…-αp1Msrpeadt+l-p1

(5)

同樣，可以通過式(4)得出下一期的方差σt+l.

1.3 基于Ornstein-Uhlenbeck模型

Ornstein-Uhlenbeck[8-10]是一類隨機過程，它是平穩的，且具有馬爾科夫性質和均值回復性質，服從正態分布.而統計套利的本質就是利用價差序列的均值回復特性進行對沖交易而獲利，因此Ornstein-Uhlenbeck過程可以用來刻畫期貨價差時間序列的均值回復特征.假設每一期的殘差序列Mspreadt服從Ornstein-Uhlenbeck過程，即

d(Mspreadt)=(-ρ·Mspreadt)dt+σdWt

(6)

式中：Wt為標準布朗運動；ρ，σ分別為常數.

對式(6)兩邊同乘以eρt并整理得

d(eρtMspreadt)=σeρtdW

(7)

對式(7)在區間[t,t+Δt]上積分并整理得

(8)

因為研究的數據為1 min高頻數據，故取Δt=1，則由式(8)可得

Mspreadt+1=b·Mspreadt+ξt

(9)

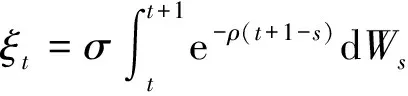
把式(9)看作是Mspreadt的自回歸過程，則可以通過對Mspreadt做一階自回歸得到b和Var(ξt)，由此得

b=-ln(ρ)

(10)

因此，可以通過Ornstein-Uhlenbeck模型來刻畫殘差序列的均值回復過程，并設計套利交易信號點.

1.4 動態套利交易策略

由于股指期貨數據不是一成不變的，隨著套利交易的不斷進行，當歷史數據離當前的時刻越久，它對于套利預測的影響就越低，其對于當前時刻的預測價值的影響效果超過處理數據的技術成本.靜態的統計套利策略很難滿足現實交易環境的需求.為此，采用滾動交易的方式[11]，即根據選定的窗口L，以前L個數據作為第一期，對其進行建模來預測第L+1個數據的殘差和方差，然后對第L+1個數據進行交易.再刪除第一個數據，以第2～(L+1)個數據作為第二期，對其進行建模來預測第L+2個數據的殘差和方差，然后對第L+2個數據進行交易，以此類推.

2 交易信號的設計

2.1 原始統計套利模型的交易信號設計

通過上述模型計算得到殘差residualt+1與下一期的方差σt+1，假設統計套利的開倉交易閥值λ1，平倉交易閥值λ2，止損交易閥值λ3，其中λ3>λ1>λ2.則在residualt+1≥|λ1σt+1|時開倉.在residualt+1≤|λ2σt+1|時平倉，當|residualt+1|≥λ3σt+1時強制平倉.

2.2 改進的統計套利模型的交易信號設計

楊立勇[12]提出了一種統計套利策略，其原理為當價差超越上邊界時建立買賣頭寸，待到將來序列波動至反向下界以下時平倉，同時再建立下一輪套利的頭寸，再到下一個時刻序列波動至上邊界以上時，進行平倉，同時再建立下一輪操作的頭寸，以此不斷的持續下去.該策略的上下邊界的取值只考慮了關于均衡價差的對稱性，在該策略基礎上，提出了改進的統計套利模型交易策略.

圖1 改進的統計套利策略交易信號示意圖Fig.1 Schematic diagram of trading signals for improved statistical arbitrage strategy

假設統計套利的上界閥值λ1，下界閥值λ2，止損交易閥值λ3，其中λ3>λ1>0>λ2.當所選的近月遠月合約的價差residualt+1>λ1σt+1或(residualt+1<λ2σt+1)時，可采用買入近月合約賣出遠月合約(或買入遠月合約賣出近月合約)的套利策略.當實施跨期套利后，如果發現residualt+1<λ2σt+1或(residualt+1>λ1σt+1)時，就將兩份合約同時平倉，套利終止.同時在合約平倉時刻的價位再次開倉，采取買入遠月合約賣出近月合約(或買入近月合約賣出遠月合約)的套利策略.直到遠近合約組合的最后一個數據.另外，為了避免較大虧損，設置止損信號，當|residualt+1|≥λ3σt+1時強制平倉.

2.3 計算最優閥值

依據總收益率最大的原則，建立以總收益率為目標函數的閥值優化模型為

s.t.λ3>λ1>λ2

其中：N為交易次數；Ri為第i次交易所得收益率.該最優化問題通過遺傳算法求解.

3 組合套利策略

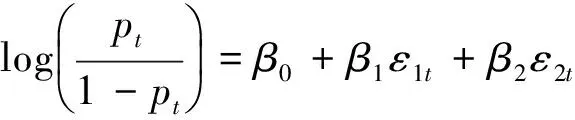
(11)

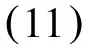
定義組合策略選擇函數為

f(yt)=ytM1+(1-yt)M2

(12)

于是，y1,y2,…,yn的似然函數為

4 實證分析

考慮股指期貨的單邊交易成本為0.000 04，保證金比率13%，合約乘數300.因為在套利交易過程中只涉及2張合約，故不考慮隱形成本[14-16].

實證數據采用2013年12月23日到2014年12月19日期間的滬深300股指期貨的當月合約和次月合約的1min數據.由于篇幅限制關系，就考慮股指期貨當月合約IF1412和下月合約IF1501的1min數據，時間段為2014年11月24日到2014年12月19日，合計20d和5 440個數據.

4.1 協整檢驗

首先，選取IF1412和IF1501的1min高頻數據序列進行平穩性分析.采用ADF(單位根)檢驗的方法，對兩序列及其一階差分序列進行平穩性檢驗，檢驗結果如表1所示.

表1 序列平穩性的檢驗結果

由表1可知：IF1412和IF1501的一階差分序列不存在單位根，為平穩序列，利用Johansen檢驗確定序列IF1412和IF1501之間的協整關系.Johansen檢驗結果表明序列IF1412和IF1501是協整的，可以進一步進行套利研究.

4.2 套利交易結果

為了檢驗策略的交易效果，從套利次數，套利成功率，累計盈利，累積收益率，年化收益率這幾個指標考察策略效果.

首先，為了比較改進后的策略和原始的套利策略的優劣，先采用原始的套利策略進行套利，選取2014年11月24日到2014年12月19日時間段的當月合約IF1412、次月合約IF1501的1 min收盤價數據為研究對象，共20 d，數據總數5 440個.通過遺傳算法得出GARCH模型的最優交易閥值為[1.333 5,-0.741 3,2.752 6]，Ornstein-Uhlenbeck模型的最優交易閥值為[0.701 9,-0.145 5,2.988 1]，套利的結果見表2.

表2 原始策略的套利結果

接著，對相同時間段數據，采用改進的統計套利策略進行套利，通過遺傳算法得出GARCH模型的最優交易閥值為[1.407 5,-0.832 9,2.998 3]，Ornstein-Uhlenbeck模型的最優交易閥值為[0.701 9,-0.145 5,2.988 1]，套利結果見表3.

表3 改進策略的套利結果

由表2，3結果可知：相比較于原始的套利策略結果，除了套利成功率這一指標外，改進后的套利策略在套利次數，套利成功次數，累積盈利等方面都比它要好很多.

4.3 組合策略實證檢驗

4.3.1 組合策略的必要性分析

從表4可以看出：采用基于GARCH的套利模型與基于Ornstein-Uhlenbeck的套利模型進行套利，各個時間段套利的套利次數、套利成功次數、累積收益率和平均單次收益率等都不存在一致變動現象，累計收益率方面，這兩種模型運用各頻率數據進行套利時，兩模型效果存在時優時劣現象.

表4 三種套利方案的月套利結果

結合GARCH模型和Ornstein-Uhlenbeck模型在統計套利的各自優勢，引入單一模型組合思想.由于單一套利模型并不在每一時段都有最優的預測效果，故有必要進行組合策略.

4.3.2 組合策略的交易規則

為了盡可能多地捕捉到套利機會，在目前倉位為空的情況下，只要基于GARCH模型和基于Ornstein-Uhlenbeck模型中的一個套利滿足開倉條件，即進行建倉，當兩模型進行套利時同時滿足各自的開倉條件時，則根據式(12)進行策略選擇.

策略平倉規則為：當目前倉位非空時，先判斷是通過哪個模型進行建倉的，然后判斷下一時刻的殘差是否滿足該模型的平倉條件.止損規則也是如此.

4.3.3 組合策略套利結果

對組合套利策略有效性進行分析，將GARCH模型套利結果、Ornstein-Uhlenbeck模型套利結果與組合策略的套利結果相比較，使用相同時間段的當月合約、次月合約的1 min歷史數據，通過遺傳算法得出，當GARCH模型的交易閥值為[1.593 0,-0.842 9,2.994 4],Ornstein-Uhlenbeck模型的交易閥值為組合策略最優閥值為[0.512 4,-0.215 4,2.941 5]，組合策略收益達到最優，其套利結果見表5.

表5 三種統計套利策略的套利結果

由表5可知：采取組合策略進行套利時，各時段的累計收益率均大于僅采取單一模型套利的累計收益率，可見該策略達到了提高整體收益率的目的，組合策略是有效的.

2014年1月—12月時間段，三種套利方案的統計套利結果如表4所示.由表4可知：2014年1月—12月時間段，采用組合策略進行統計套利時，其累計收益率均大于采取單一模型進行套利時的累計收益率，組合策略具有普遍適用性.

5 結 論

在改進的統計套利策略的基礎上，將組合思想引入到統計套利策略中，并利用1min的高頻數據進行實證分析.采用滬深300股指期貨近月遠月合約的1 min真實數據，用動態的交易方式對改進的套利交易策略和模型進行檢驗分析.與原始的統計策略相比較，改進的套利策略從套利次數、套利成功次數、累計盈利和年化收益率等方面都比它要好很多.在改進的統計套利策略基礎上，結合GARCH模型和Ornstein-Uhlenbeck模型在統計套利的各自優勢，引入伯努利隨機變量將兩模型進行組合，并進行實證檢驗.通過將GARCH模型套利結果、Ornstein-Uhlenbeck模型套利結果與組合策略的套利結果進行比較分析，發現總體收益均提高了，采用組合策略進行統計套利顯著優于采取單一模型的策略.

[1] NIKOS S T, NICK K, GEORGE D D. An intelligent statistical arbitrage trading system[C]//Hellenic Conference on Advances in Artificial Intelligence. Greece: Springer-Verlag,2006:596-599.

[2] THOMAIDIS N S. Efficient statistical analysis of financial time-series using neural networks and garch models[J]. Social science electronic publishing,2007,92(6):253-262.

[3] TRIANTAFYLLOPOULOS K, MONTANA G. Dynamic modeling of mean-reverting spreads for statistical arbitrage[J]. Computational management science,2008,8(1):23-49.

[4] 伍娟.高頻數據下基于成對交易的統計套利策略研究[D].長沙：中南大學,2010.

[5] 楊懷東.高頻數據下基于組合預測思想的統計套利策略創新設計與實證研究[J].財務與金融，2012(4):80-87.

[6] 王紅麗.基于狀態轉移的股指期貨波動時變組合預測研究[D].重慶：重慶師范大學，2011.

[7] 張福余.基于狀態空間模型的高頻數據統計套利研究[D].桂林：廣西師范大學,2014.

[8] 顏涵.基于股指期貨高頻數據的統計套利研究[D].長沙：湖南大學，2012.

[9] 李靜.基于GARCH和Ornstein-Uhlenbeck模型的統計套利策略實證分析——以天膠期貨跨期套利為例[D].大連：東北財經大學，2013.

[10] UHLENBECK G E, ORNSTEIN L S. On the theory of Brownian motion[J]. Physical review，1930，36(3)：823-841.

[11] 丁鵬.量化投資—策略與技術[M].北京：電子工業出版社，2012.

[12] 楊立勇.基于統計套利理論的股指期貨跨期套利研究[D].上海：東華大學，2012.

[13] WONG C S, LI W K. On a logistic mixture autoregressive model[J]. Biometrika,2001,88(3):833-846.

[14] 周明華，孫長啟，陳淑敏，等.基于動態均衡價差的股指期貨的跨期套利研究[J].浙江工業大學學報,2016,44(1):111-118.

[15] 原俊青，張振宇，王理同，等.基于極值理論的VaR度量模型及實證研究[J].浙江工業大學學報，2013,41(5)：578-582.

[16] 周明華，俞偉，陸川，等.動態網絡中行業因素與股市波動性研究[J].浙江工業大學學報，2015,43(3)：350-354.

(責任編輯：劉 巖)

Research on the combination strategy of statistical arbitrage based on high-frequency data

ZHOU Minghua1, ZHOU Tingting2, ZHANG Minkai2

(1.Jianxing Honors College, Zhejiang University of Technology, Hangzhou 310023, China; 2.College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

On the basis of the thought of combination strategy, a new combination strategy of statistical arbitrage which combine GARCH(generalized autoregressive conditional heteroskedastic) model and Ornstein-Uhlenbeck model by introducing into Bernoulli random variable is developed, then we arbitrage on the basis of the improved statistical arbitrage strategy. The validity of the model and the actual trading effects has been tested by the dynamic methods. The results of empirical test show that it is necessary to combine the single arbitrage models, and the overall income level of the combination strategy compared to that of single strategy is significantly improved.

high-frequency data; GARCH; Ornstein-Uhlenbeck; combination strategy; Bernoulli variable

2016-10-13

周明華(1959—)，男，浙江紹興人，教授，研究方向為金融數學，E-mail：mhzhou@zjut.edu.cn.

F832.48

A

1006-4303(2017)03-0336-06