單盤式浮頂油罐內(nèi)含蠟原油溫降規(guī)律數(shù)值計(jì)算研究

王敏，李敬法，張欣雨，宇波

1 油氣管道輸送安全國(guó)家工程實(shí)驗(yàn)室/城市油氣輸配技術(shù)北京市重點(diǎn)實(shí)驗(yàn)室/中國(guó)石油大學(xué)(北京)，北京 102249 2 中國(guó)石油化工集團(tuán)國(guó)際石油勘探開(kāi)發(fā)公司，北京 100029 3 機(jī)械工程學(xué)院，北京石油化工學(xué)院，北京 102617

單盤式浮頂油罐內(nèi)含蠟原油溫降規(guī)律數(shù)值計(jì)算研究

王敏1，李敬法1，張欣雨2，宇波3*

1 油氣管道輸送安全國(guó)家工程實(shí)驗(yàn)室/城市油氣輸配技術(shù)北京市重點(diǎn)實(shí)驗(yàn)室/中國(guó)石油大學(xué)(北京)，北京 102249 2 中國(guó)石油化工集團(tuán)國(guó)際石油勘探開(kāi)發(fā)公司，北京 100029 3 機(jī)械工程學(xué)院，北京石油化工學(xué)院，北京 102617

建立了考慮含蠟原油非牛頓性和析蠟相變過(guò)程的單盤式浮頂油罐內(nèi)含蠟原油溫降物理數(shù)學(xué)模型，并發(fā)展了一體化耦合求解方法。模型中，采用冪律方程描述罐內(nèi)含蠟原油的非牛頓特性；采用湍流大渦模擬方法計(jì)算罐內(nèi)含蠟原油的湍流流動(dòng)過(guò)程；采用焓多孔介質(zhì)理論計(jì)算罐內(nèi)含蠟原油的析蠟相變過(guò)程，并跟蹤罐內(nèi)含蠟原油的相變界面。利用文獻(xiàn)中的結(jié)果對(duì)本文模型進(jìn)行驗(yàn)證。基于驗(yàn)證的程序，對(duì)實(shí)際單盤式浮頂油罐內(nèi)含蠟原油溫降過(guò)程進(jìn)行計(jì)算，研究罐內(nèi)含蠟原油溫降過(guò)程的演化規(guī)律，并對(duì)罐頂、罐底凝油層的增長(zhǎng)以及罐頂、罐底和罐壁處傳熱量的變化規(guī)律進(jìn)行研究。研究結(jié)果可為單盤式浮頂油罐的設(shè)計(jì)和生產(chǎn)方案的制定提供一定的指導(dǎo)。

單盤式浮頂油罐；溫降規(guī)律；非牛頓性；析蠟相變；大渦模擬

0 背景

中國(guó)所產(chǎn)原油大多為含蠟原油。含蠟原油具有易凝、高黏、流變性復(fù)雜等特點(diǎn)，在實(shí)際生產(chǎn)儲(chǔ)存中通常需要加熱處理。單盤式浮頂油罐是常用的含蠟原油儲(chǔ)罐之一[1]。含蠟原油在罐內(nèi)儲(chǔ)存時(shí)會(huì)向外界環(huán)境放熱而被冷卻。當(dāng)油溫降低到含蠟原油析蠟點(diǎn)時(shí)，含蠟原油開(kāi)始析蠟；當(dāng)析蠟分?jǐn)?shù)達(dá)到原油總質(zhì)量的2%～3%時(shí)，含蠟原油將會(huì)膠凝[2]，嚴(yán)重影響實(shí)際生產(chǎn)，甚至造成生產(chǎn)事故。研究單盤式浮頂油罐內(nèi)含蠟原油的溫降過(guò)程，準(zhǔn)確把握罐內(nèi)含蠟原油的溫降規(guī)律，對(duì)科學(xué)設(shè)計(jì)浮頂油罐的保溫結(jié)構(gòu)、合理制定浮頂油罐的周轉(zhuǎn)方案具有重要意義。

目前，研究油罐內(nèi)含蠟原油溫降規(guī)律的方法主要有兩種：實(shí)驗(yàn)研究[3-5]和數(shù)值模擬研究[6-9]，其中數(shù)值模擬因?yàn)橥顿Y小、研究周期短以及研究結(jié)果全面等優(yōu)點(diǎn)成為近年來(lái)最主要的研究手段。在數(shù)值模擬研究方面，Lin等[6]采用數(shù)值計(jì)算方法對(duì)高徑比為1/3～1，Pr數(shù)為1～1 000、Ra數(shù)為6×106～6×1010的油罐內(nèi)溫降規(guī)律進(jìn)行研究。在此基礎(chǔ)上，采用尺度分析方法擬合了無(wú)量綱溫度與時(shí)間、儲(chǔ)罐高徑比、Pa數(shù)和Ra數(shù)的關(guān)系式。Oliveski等[7]采用實(shí)驗(yàn)方法和數(shù)值計(jì)算方法對(duì)Ra數(shù)分別為3.1×109和4.3×109的實(shí)驗(yàn)油罐內(nèi)原油溫降15 h的原油溫度場(chǎng)和速度場(chǎng)進(jìn)行計(jì)算，給出了不同溫降時(shí)間下，油罐豎直中心線上的油溫分布以及罐頂和罐壁處原油的速度矢量場(chǎng)分布。Oliveski[8]采用有限容積法對(duì)不同容積的實(shí)驗(yàn)罐內(nèi)原油的溫降過(guò)程展開(kāi)研究，并采用量綱分析法回歸了油罐的平均Nu數(shù)與儲(chǔ)罐無(wú)量綱高徑比、無(wú)量綱總傳熱系數(shù)以及Ra數(shù)和Pr數(shù)的換熱關(guān)聯(lián)式。李旺[9]采用大渦模擬方法對(duì)10萬(wàn)方雙盤式浮頂油罐內(nèi)原油溫降過(guò)程進(jìn)行計(jì)算，并分析了浮盤類型、保溫層厚度、液位、油品物性、太陽(yáng)輻射以及風(fēng)速對(duì)罐內(nèi)原油溫降過(guò)程的影響。研究發(fā)現(xiàn)，浮盤類型、保溫層厚度、液位和太陽(yáng)輻射對(duì)油罐溫降過(guò)程具有較大影響，而風(fēng)速和油品物性對(duì)油罐溫降過(guò)程影響較小。

雖然國(guó)內(nèi)外學(xué)者已經(jīng)對(duì)單盤式浮頂油罐內(nèi)原油的溫降規(guī)律開(kāi)展了一定的研究，但這些研究通常將原油簡(jiǎn)化為牛頓流體，沒(méi)有考慮含蠟原油的析蠟相變過(guò)程。而且研究中往往只給出油罐內(nèi)某些特定位置處油溫隨溫降時(shí)間的變化。就作者查閱的文獻(xiàn)而言，目前還沒(méi)有見(jiàn)到全面研究罐內(nèi)含蠟原油溫降演化規(guī)律以及罐內(nèi)含蠟原油湍流流動(dòng)與傳熱特性的研究成果。基于此，本文建立了考慮含蠟原油非牛頓性和析蠟相變過(guò)程的單盤式浮頂油罐內(nèi)含蠟原油湍流溫降物理數(shù)學(xué)模型，并發(fā)展了一體化耦合求解技術(shù)。通過(guò)對(duì)實(shí)際單盤式浮頂油罐內(nèi)原油溫降過(guò)程進(jìn)行計(jì)算，研究罐內(nèi)含蠟原油溫度場(chǎng)及流場(chǎng)的演化規(guī)律，并對(duì)凝油層增長(zhǎng)以及傳熱量變化進(jìn)行分析。

1 物理數(shù)學(xué)模型及定解條件

1.1 物理模型

單盤式浮頂油罐包括：鋼板層、保溫層和含蠟原油，其傳熱過(guò)程包括液固(含蠟原油與鋼板層)，固固(鋼板層和保溫層)耦合傳熱以及罐體與外界大氣之間強(qiáng)制對(duì)流換熱和油罐與罐底土壤層之間的導(dǎo)熱。因此，單盤式浮頂油罐的傳熱過(guò)程非常復(fù)雜，計(jì)算難度較大。

對(duì)含蠟原油溫降過(guò)程分析發(fā)現(xiàn)，初始時(shí)刻含蠟原油溫度較高，含蠟原油以純液態(tài)形式存在，且表現(xiàn)出牛頓流體特性；當(dāng)油溫開(kāi)始降低到含蠟原油析蠟點(diǎn)Tw(含蠟原油中開(kāi)始有蠟晶析出時(shí)的溫度)以下時(shí)，含蠟原油中開(kāi)始有蠟晶析出，固液分散體系開(kāi)始形成。此時(shí)含蠟原油仍然表現(xiàn)出牛頓流體特性；當(dāng)油溫降低到含蠟原油反常點(diǎn)Ta(牛頓流體與非牛頓流體的轉(zhuǎn)換溫度)以下時(shí)，含蠟原油開(kāi)始表現(xiàn)出非牛頓流體特性，此時(shí)含蠟原油仍以固液分散體系形式存在；當(dāng)油溫繼續(xù)降低到含蠟原油顯觸點(diǎn)Tt(含蠟原油顯現(xiàn)觸變性的最高溫度)以下時(shí)，含蠟原油中析出的蠟晶開(kāi)始發(fā)生交聯(lián)，形成蠟晶多孔介質(zhì)結(jié)構(gòu)[2]。表1給出了溫降過(guò)程中含蠟原油的狀態(tài)以及流變性的變化過(guò)程。

由于實(shí)際單盤式浮頂油罐的尺寸較大，罐內(nèi)含蠟原油傳熱方式為湍流自然對(duì)流(實(shí)際1 000方單盤式浮頂油罐半徑為6 m，當(dāng)溫差為30 ℃時(shí)，罐內(nèi)含蠟原油Ra數(shù)高達(dá)2.0×1013)，因此要對(duì)這樣的三維實(shí)際油罐進(jìn)行數(shù)值計(jì)算，其計(jì)算難度和計(jì)算量都將非常大，計(jì)算非常耗時(shí)。考慮到單盤式浮頂油罐的對(duì)稱性，本文將三維油罐簡(jiǎn)化為二維油罐，如圖1所示。采用湍流大渦模擬方法對(duì)考慮含蠟原油的非牛頓性和析蠟相變過(guò)程的單盤式浮頂油罐內(nèi)含蠟原油湍流溫降過(guò)程進(jìn)行計(jì)算，研究罐內(nèi)含蠟原油的溫降規(guī)律。

表1 溫降過(guò)程中含蠟原油的狀態(tài)和流變性變化Table 1 The state and rheological behavior of waxy crude oil in temperature drop process

圖1 二維單盤式浮頂油罐物理模型Fig. 1 Sketch map of single-plate fl oating roof oil tank

1.2 數(shù)學(xué)模型

對(duì)浮頂油罐內(nèi)含蠟原油溫降過(guò)程分析發(fā)現(xiàn)，其本質(zhì)是一個(gè)非穩(wěn)態(tài)自然對(duì)流過(guò)程，其中涉及相變、固液相作用、非牛頓性、流固耦合以及湍流。結(jié)合1.1節(jié)建立的單盤式浮頂油罐溫降物理模型，建立考慮含蠟原油非牛頓性[2,10-11]和析蠟相變過(guò)程[12-14]的單盤式浮頂油罐內(nèi)含蠟原油湍流溫降數(shù)學(xué)模型。考慮到物理模型中涉及到流固耦合，為了實(shí)現(xiàn)一體化耦合求解，將固體(鋼板層和保溫層)區(qū)域設(shè)定為黏度為無(wú)窮大的流體，其余參數(shù)按照實(shí)際參數(shù)取值。此外，本文采用大渦模擬方法[15]計(jì)算罐內(nèi)含蠟原油的湍流過(guò)程。二維圓柱坐標(biāo)系下單盤式浮頂油罐溫降控制方程如式(1)～(4)所示：

其中，ρ、β和cp分別為密度、體積膨脹系數(shù)和定壓熱容。和分別為采用大渦模擬方法過(guò)濾后x方向和r方向的速度分量、壓力和溫度。sux和sur為蠟晶多孔介質(zhì)對(duì)含蠟原油的束縛作用，本文稱之為達(dá)西源項(xiàng)。sh為含蠟原油析蠟潛熱項(xiàng)。含蠟原油的析蠟相變處理方法將在下文中詳細(xì)介紹。μeff和λeff分別為有效黏度和有效導(dǎo)熱系數(shù)，本文中將分別由式(5)和式(6)計(jì)算：

其中，μt和αt分別為亞格子渦黏系數(shù)和亞格子渦擴(kuò)散系數(shù)。亞格子渦黏系數(shù)的構(gòu)造是大渦模擬方法的關(guān)鍵，本文中將采用Smagorinshy-Lilly模型[16]構(gòu)造，具體表達(dá)式如式(7)所示：

式中，Ls為亞格子混合長(zhǎng)度，其定義式為L(zhǎng)s=min(κd, CsΔ)[16]。混合長(zhǎng)度的計(jì)算中考慮了邊界效應(yīng)，對(duì)近壁區(qū)做了壁面修正；κ為馮卡門常數(shù)，本文中取0.41；d為計(jì)算位置距最近邊界的距離；Cs為模型常數(shù)，本文中取0.1；Δ為過(guò)濾尺寸。

對(duì)于亞格子渦擴(kuò)散系數(shù)，本文中采用式(8)計(jì)算。其中，Prt取0.87[16]。

1.2.1 非牛頓性

當(dāng)油溫降低到含蠟原油的反常點(diǎn)以下時(shí)，含蠟原油為假塑性流體，其剪應(yīng)力與剪切率的關(guān)系可由冪律方程很好地描述。此外，當(dāng)油溫繼續(xù)降低到含蠟原油顯觸點(diǎn)以下一定范圍內(nèi)時(shí)，冪律方程仍能很好的描述觸變性含蠟原油的剪應(yīng)力與剪切率的關(guān)系[2]，因此選擇冪律方程描述含蠟原油的非牛頓性。式(9)給出了含蠟原油的表觀黏度μa與剪切率˙之間的關(guān)系式。

其中，K為稠度系數(shù)，單位為Pa·sn；n為流動(dòng)特性指數(shù)。K和n與油溫T的關(guān)系由實(shí)驗(yàn)數(shù)據(jù)擬合得到。為罐內(nèi)含蠟原油的剪切率，由式(10)計(jì)算[17]。

1.2.2 析蠟相變過(guò)程

當(dāng)油溫降低到含蠟原油析蠟點(diǎn)以下時(shí)，含蠟原油開(kāi)始析蠟。此時(shí)，析出的蠟晶漂浮在含蠟原油中，隨著含蠟原油一起流動(dòng)。當(dāng)油溫降低到含蠟原油顯觸點(diǎn)以下時(shí)，析出的蠟晶開(kāi)始相互交聯(lián)，形成蠟晶多孔介質(zhì)結(jié)構(gòu)，并對(duì)包裹在其孔隙中的含蠟原油產(chǎn)生束縛。隨著油溫的繼續(xù)降低，蠟晶多孔介質(zhì)孔隙度逐漸減小，束縛作用逐漸增強(qiáng)。本文采用達(dá)西定律描述這種束縛作用，達(dá)西源項(xiàng)的表達(dá)式如式(11)和式(12)所示。

其中，K0為滲透率常數(shù)，本文中取10-7[14,18]。gs為析蠟分?jǐn)?shù)，即某一溫度下，含蠟原油中析出的蠟晶質(zhì)量占原油總質(zhì)量的比例，由DSC實(shí)驗(yàn)確定。

含蠟原油在析蠟相變過(guò)程中還將釋放相變潛熱，相變潛熱表現(xiàn)為能量方程中的源項(xiàng)sh，如式(14)所示：

式中，ΔH為相變潛熱。本文中ΔH=(1-gs)L，L為含蠟原油的析蠟相變總潛熱。

1.3 邊界條件和初始條件

1.3.1 邊界條件

單盤式浮頂油罐罐頂、罐壁以及浮頂油罐右側(cè)土壤表層均為第三類邊界條件，其對(duì)流換熱系數(shù)為25.63 W/(m2·℃)[2]。油罐中心軸為對(duì)稱邊界，土壤層右邊界為絕熱邊界，下邊界為恒溫邊界，溫度取10 ℃。此外，在油罐邊界條件設(shè)定中，包含了外界氣溫，本文以中國(guó)某地區(qū)11月到12月的實(shí)測(cè)氣溫為基礎(chǔ)數(shù)據(jù)來(lái)計(jì)算。

1.3.2 初始條件

本文中規(guī)定初始時(shí)刻罐內(nèi)含蠟原油、空氣層、鋼板層和保溫層的溫度均為30 ℃。地表溫度為初始時(shí)刻的外界氣溫，為1 ℃。不同深度處的土壤溫度由土壤恒溫層和地表溫度線性插值得到。

2 數(shù)值計(jì)算方法及模型驗(yàn)證

2.1 數(shù)值計(jì)算方法

本文采用有限容積法對(duì)控制方程進(jìn)行離散，其中對(duì)流項(xiàng)采用GAMMA格式[19]離散，擴(kuò)散項(xiàng)采用中心差分格式離散，時(shí)間項(xiàng)采用一階全隱格式離散。采用基于非均分同位網(wǎng)格的SIMPLE算法耦合壓力和速度，求解器選用強(qiáng)隱方法[20]。為提高計(jì)算速度，本文采用多重網(wǎng)格方法求解罐底土壤溫度場(chǎng)，采用一體化求解方法對(duì)油罐部分(包括罐頂空氣層和鋼板層、罐底鋼板層和罐壁保溫層)溫度場(chǎng)和流場(chǎng)等進(jìn)行計(jì)算，再與罐底土壤溫度場(chǎng)進(jìn)行耦合。如此反復(fù)，直至兩部分均達(dá)到收斂標(biāo)準(zhǔn)為止。本文中時(shí)間步長(zhǎng)取5 s。此時(shí)收斂標(biāo)準(zhǔn)為：油罐部分質(zhì)量不平衡量小于10-4，罐底土壤層導(dǎo)熱方程余量小于10-6。

另一個(gè)關(guān)鍵問(wèn)題是相變潛熱ΔH的更新。在數(shù)值計(jì)算中，每個(gè)時(shí)層內(nèi)相變潛熱根據(jù)各時(shí)層內(nèi)油溫進(jìn)行更新，相變潛熱能否正確更新會(huì)直接影響計(jì)算過(guò)程的穩(wěn)定性和收斂性。本文采用式(15)更新相變潛熱[12]。

其中，α為亞松弛因子，本文中取0.2；m和m-1分別為當(dāng)前迭代步和上一迭代步；為相變潛熱的反函數(shù)[12]，即含蠟原油溫度。根據(jù)前面的分析可知，當(dāng)油溫低于含蠟原油析蠟點(diǎn)時(shí)，ΔH=(1.0-gs)L，析蠟分?jǐn)?shù)gs與油溫之間的關(guān)系可以由DSC實(shí)驗(yàn)測(cè)得，由此，可以得到的計(jì)算式。

根據(jù)建立的單盤式浮頂油罐溫降物理數(shù)學(xué)模型，本文采用Fortran語(yǔ)言編寫了計(jì)算程序，相應(yīng)的程序設(shè)計(jì)流程圖如圖2所示。

以實(shí)際1 000方的單盤式浮頂油罐為例，對(duì)其溫降規(guī)律展開(kāi)研究。其中1 000方單盤式浮頂油罐的尺寸x1、x2、x3、x4、r1、r2和r3分別為-5.0 m、0.01 m、8.01 m、8.02 m、6.0 m、6.11 m和11.11 m[1]。罐內(nèi)含蠟原油、空氣層、鋼板層、土壤層和保溫層的物性如表2。

考慮非牛頓性和析蠟相變過(guò)程的含蠟原油黏度由式(16)計(jì)算。

含蠟原油的表觀黏度μa由式(9)計(jì)算得到。其中，稠度系數(shù)K和流動(dòng)特性指數(shù)n由實(shí)驗(yàn)數(shù)據(jù)擬合得到，本文中的計(jì)算式見(jiàn)式(17)和(18)。

對(duì)含蠟原油進(jìn)行DSC實(shí)驗(yàn)，擬合得到析蠟分?jǐn)?shù)gs與油溫T的關(guān)系見(jiàn)式(19)。

根據(jù)析蠟潛熱ΔH、析蠟分?jǐn)?shù)gs及油溫的關(guān)系，可以推導(dǎo)出f-1(ΔH)的表達(dá)式如式(20)。

其中，含蠟原油的析蠟點(diǎn)Tw、反常點(diǎn)Ta和顯觸點(diǎn)Tt分別為27 ℃、25 ℃和23 ℃。

圖2 程序設(shè)計(jì)流程圖Fig. 2 Flow chart of the calculation program

2.2 大渦模擬方法驗(yàn)證

為了驗(yàn)證大渦模擬方法的準(zhǔn)確性，本文在102×102的非均分網(wǎng)格上對(duì)直角坐標(biāo)系方腔內(nèi)Pr數(shù)和Ra數(shù)分別為0.71和1.58×109的湍流自然對(duì)流過(guò)程進(jìn)行計(jì)算，將計(jì)算結(jié)果與文獻(xiàn)中的實(shí)驗(yàn)結(jié)果[21]進(jìn)行比較。圖3給出了由本文大渦模擬方法計(jì)算的方腔水平中心線上無(wú)量綱溫度Θ和無(wú)量綱速度Uy與文獻(xiàn)結(jié)果的比較，從圖中可以看出，本文計(jì)算結(jié)果與文獻(xiàn)中的實(shí)驗(yàn)結(jié)果吻合良好。

2.3 非牛頓流體模型驗(yàn)證

為了驗(yàn)證非牛頓流體模型的準(zhǔn)確性，在102×102的均分網(wǎng)格上，對(duì)Pr數(shù)為100，Ra數(shù)分別為104和105的方腔非牛頓流體穩(wěn)態(tài)自然對(duì)流過(guò)程進(jìn)行計(jì)算，并將計(jì)算得到的熱邊界平均Nu數(shù)與文獻(xiàn)中的結(jié)果[10,11]進(jìn)行比較，結(jié)果如表3所示。從表中可以看出，本文計(jì)算結(jié)果與文獻(xiàn)結(jié)果吻合良好。

2.4 相變模型驗(yàn)證

為了驗(yàn)證相變模型的正確性，本文采用流固耦合方法對(duì)半徑為31.9 mm，高為59.8 mm，壁面和底部包裹有厚度分別為2.85 mm的聚碳酸酯和5.97 mm聚丙烯酸固體保溫材料的圓柱形區(qū)域內(nèi)正二十烷的融化過(guò)程進(jìn)行計(jì)算。計(jì)算中，正二十烷的初始溫度為23 ℃，相變溫度為36.4 ℃，頂部絕熱，壁面和底部溫度分別為45 ℃和32 ℃，物性等其他數(shù)據(jù)參見(jiàn)Jones等文獻(xiàn)[13]。圖4(a)給出了融化9601.6 s后區(qū)域內(nèi)正二十烷的融化界面位置以及液態(tài)正二十烷中的溫度場(chǎng)和速度矢量場(chǎng)分布。圖4(b)給出了不同融化時(shí)間下，區(qū)域內(nèi)正二十烷融化界面位置與實(shí)驗(yàn)結(jié)果的對(duì)比，從圖中可以看出，本文計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果[13]吻合良好。

表2 含蠟原油、空氣層、鋼板層、土壤層和保溫層的物性Table 2 Thermo-physical properties of different materials

3 單盤式浮頂油罐內(nèi)含蠟原油溫降規(guī)律研究

3.1 單盤式浮頂油罐溫度場(chǎng)演化

圖5給出了不同溫降時(shí)刻，1000 m3單盤式浮頂油罐內(nèi)含蠟原油溫度場(chǎng)和速度矢量場(chǎng)分布。對(duì)圖5進(jìn)行分析可知，初始時(shí)刻，罐底部含蠟原油溫度為30 ℃，土壤表層溫度僅為1 ℃，熱量快速?gòu)墓迌?nèi)含蠟原油傳入罐底土壤層，罐底含蠟原油中形成了層狀分布的溫度場(chǎng)，如圖5(a)。而且，在這一階段，罐頂部含蠟原油將通過(guò)灌頂鋼板層向外界大氣傳熱，同時(shí)罐頂部含蠟原油損失的熱量將通過(guò)浮升力，以自然對(duì)流方式從油罐中部獲得補(bǔ)充，湍流自然對(duì)流過(guò)程開(kāi)始形成。此時(shí)，流動(dòng)過(guò)程僅限于油罐右上部，如圖6(a)。隨著溫降過(guò)程的繼續(xù)進(jìn)行，罐內(nèi)含蠟原油湍流流動(dòng)區(qū)域逐漸擴(kuò)展，溫降100 h時(shí)，湍流自然對(duì)流區(qū)域逐漸擴(kuò)展整個(gè)油罐區(qū)域，罐內(nèi)x方向最大流速達(dá)到0.03 m/s，如圖5(b)，罐底部層狀分布的溫度場(chǎng)消失，罐內(nèi)油溫近似均勻，且整體發(fā)生溫降，如圖5(b)～圖5(c)。當(dāng)罐內(nèi)油溫降低到含蠟原油顯觸點(diǎn)(23 ℃)以下時(shí)，罐內(nèi)含蠟原油中析出的蠟晶開(kāi)始相互交聯(lián)，形成蠟晶多孔介質(zhì)結(jié)構(gòu)，并對(duì)包裹在其孔隙中的含蠟原油產(chǎn)生束縛，傳熱方式由固液分散體系自然對(duì)流轉(zhuǎn)變?yōu)橄灳Ф嗫捉橘|(zhì)傳熱，類似于導(dǎo)熱，此時(shí)，罐內(nèi)含蠟原油流動(dòng)過(guò)程明顯減弱。溫降300 h時(shí)，罐內(nèi)x方向最大流速僅約為4.0×10-4m/s，如圖5(d)。而且在罐頂、罐底和罐壁冷量的共同作用下，罐內(nèi)出現(xiàn)了明顯的冷熱油界面，如圖5(d)～圖5(f)。

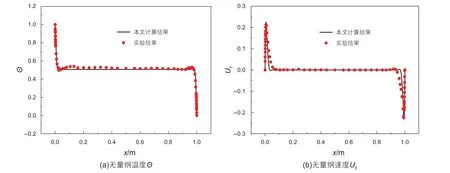
圖3 大渦模擬方法驗(yàn)證Fig. 3 Validation of LES method

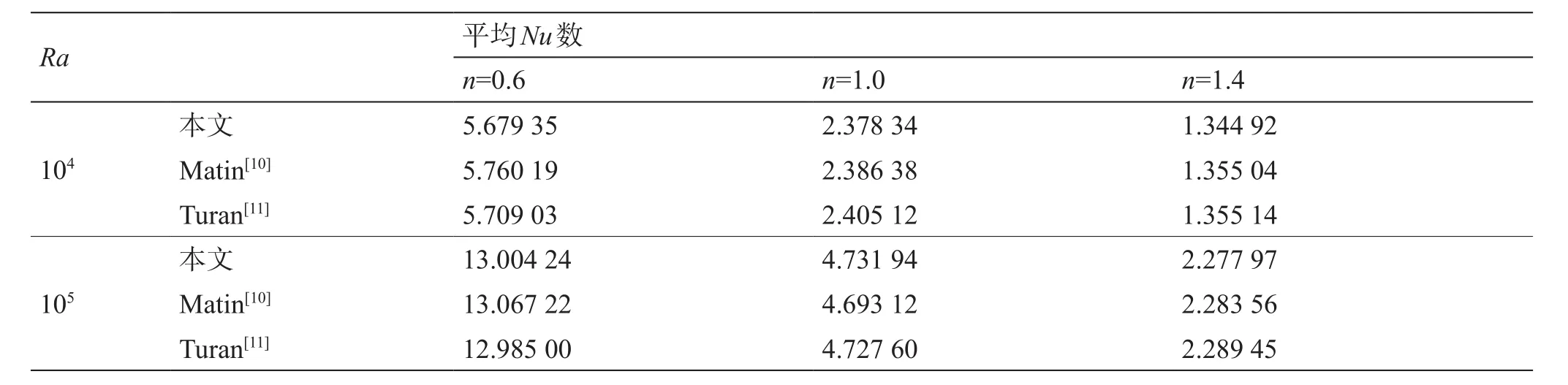
表3 Pr=100時(shí)，本文計(jì)算的方腔熱邊界平均Nu數(shù)與文獻(xiàn)結(jié)果的對(duì)比Table 3 Comparison of Nu at the high temperature boundary with the numerical results obtained by this paper, Matin[10]and Turan[11]when Pr=100

圖6給出了不同溫降時(shí)刻，1 000方單盤式浮頂油罐內(nèi)含蠟原油流函數(shù)的分布。值得指出的是，流函數(shù)的分布反映了罐內(nèi)含蠟原油的流動(dòng)情況。從圖中可以看出，罐內(nèi)流函數(shù)演化過(guò)程可以分為兩個(gè)階段：(1)溫降時(shí)間小于200 h。在這一階段，罐內(nèi)核心區(qū)油溫高于含蠟原油的顯觸點(diǎn)，核心區(qū)含蠟原油以純液態(tài)或固液分散體系形式存在，流動(dòng)性較好。而且隨外界氣溫的劇烈波動(dòng)，罐內(nèi)流函數(shù)處于瞬態(tài)變化之中。此外，在外界大氣冷量以及罐內(nèi)湍流自然對(duì)流作用下，罐內(nèi)含蠟原油的流動(dòng)在整個(gè)油罐區(qū)域內(nèi)進(jìn)行。(2)溫降300～600 h。在這一階段，罐內(nèi)核心區(qū)油溫已經(jīng)降低到含蠟原油顯觸點(diǎn)以下，蠟晶多孔介質(zhì)結(jié)構(gòu)已經(jīng)形成，含蠟原油的流動(dòng)性明顯減弱，表現(xiàn)為流函數(shù)值僅約為溫降200 h的1%。隨著油溫繼續(xù)降低，析蠟量繼續(xù)增大，蠟晶多孔介質(zhì)孔隙度繼續(xù)減小，流動(dòng)性繼續(xù)減弱。在外界大氣冷量作用下，罐內(nèi)含蠟原油的流動(dòng)僅限于油罐右上部。

圖4 正二十烷融化過(guò)程中不同時(shí)刻融化界面位置與實(shí)驗(yàn)數(shù)據(jù)對(duì)比Fig. 4 The comparison between calculated values and experimental results

當(dāng)罐內(nèi)含蠟原油還未完全膠凝時(shí)，單盤式浮頂油罐內(nèi)油溫近似均勻，且整體發(fā)生溫降，本文稱之為油罐核心區(qū)。本文通過(guò)考察罐內(nèi)x=6.16 m，r=4.18 m處的油溫變化來(lái)研究核心區(qū)含蠟原油溫降情況，通過(guò)考察罐內(nèi)平均油溫來(lái)研究油罐整體溫降情況，計(jì)算結(jié)果如圖7所示。其中，平均油溫＜T＞由式(21)計(jì)算。式中，為罐內(nèi)第i、j控制容積的油溫，ΔVij為第i、j控制容積的體積。

圖7給出了單盤式浮頂油罐核心區(qū)油溫和平均油溫隨溫降時(shí)間的變化曲線。從圖中可以看出，核心區(qū)溫降曲線存在兩個(gè)轉(zhuǎn)折點(diǎn)：含蠟原油的析蠟點(diǎn)(27 ℃)和顯觸點(diǎn)(23 ℃)。具體分析可知，當(dāng)油溫降低到含蠟原油析蠟點(diǎn)以下時(shí)，含蠟原油中開(kāi)始有蠟晶析出，并釋放析蠟潛熱。而析蠟潛熱的釋放會(huì)對(duì)罐內(nèi)含蠟原油溫降過(guò)程起到緩沖作用。當(dāng)油溫繼續(xù)降低到含蠟原油顯觸點(diǎn)以下時(shí)，罐內(nèi)已經(jīng)析出的蠟晶開(kāi)始相互交聯(lián)，形成蠟晶多孔介質(zhì)結(jié)構(gòu)，造成罐內(nèi)含蠟原油的傳熱方式從自然對(duì)流轉(zhuǎn)變?yōu)橄灳Ф嗫捉橘|(zhì)傳熱，類似于導(dǎo)熱，從而使得罐內(nèi)含蠟原油的傳熱過(guò)程明顯變慢。此外，當(dāng)油溫降低到含蠟原油顯觸點(diǎn)以下時(shí)，析蠟潛熱的傳遞，以及油溫降低后從核心區(qū)獲得的熱量補(bǔ)償均變慢，在二者的共同作用下，罐內(nèi)溫降過(guò)程出現(xiàn)了階梯狀下降的特點(diǎn)，這與文獻(xiàn)中水冷凝的實(shí)驗(yàn)結(jié)果[22]類似。

此外，從圖7中還可以看出，當(dāng)油溫高于含蠟原油顯觸點(diǎn)時(shí)，罐內(nèi)核心區(qū)油溫與平均油溫近似相等，而當(dāng)油溫降低到顯觸點(diǎn)以下時(shí)，核心區(qū)油溫與平均油溫的差異逐漸顯現(xiàn)。這是因?yàn)椋?dāng)罐內(nèi)油溫高于含蠟原油顯觸點(diǎn)時(shí)，罐內(nèi)含蠟原油傳熱方式為湍流自然對(duì)流，在湍流自然對(duì)流過(guò)程的攪動(dòng)下，罐內(nèi)油溫近似均勻，核心區(qū)油溫與平均油溫近似相等。當(dāng)油溫降低到含蠟原油顯觸點(diǎn)以下時(shí)，罐內(nèi)含蠟原油已經(jīng)膠凝，從罐頂、罐底和罐壁處傳入的冷量開(kāi)始冷卻罐內(nèi)含蠟原油，罐內(nèi)出現(xiàn)了明顯的溫度梯度，如圖5(d)～圖5(f)，核心區(qū)油溫將明顯高于平均油溫。

3.2 單盤式浮頂油罐罐底和罐頂凝油層的增長(zhǎng)

當(dāng)油溫降低到含蠟原油顯觸點(diǎn)以下時(shí)，罐內(nèi)含蠟原油中析出的蠟晶開(kāi)始相互交聯(lián)，逐漸形成蠟晶多孔介質(zhì)結(jié)構(gòu)。該結(jié)構(gòu)一旦形成就會(huì)嚴(yán)重束縛含蠟原油，造成含蠟原油流動(dòng)性顯著變差。因此，含蠟原油的顯觸點(diǎn)可看成凝油層開(kāi)始形成的臨界溫度。

圖5 不同溫降時(shí)刻，罐內(nèi)含蠟原油溫度場(chǎng)和速度矢量場(chǎng)分布Fig. 5 Oil temperature and velocity vector distributions in the tank at different moments

圖8給出了單盤式浮頂油罐內(nèi)r=5.52 m處罐頂和罐底凝油層隨溫降時(shí)間的增長(zhǎng)。從圖中可以看出，隨著溫降過(guò)程的進(jìn)行，罐頂和罐底凝油層均表現(xiàn)出指數(shù)增長(zhǎng)的特點(diǎn)。當(dāng)罐內(nèi)含蠟原油完全膠凝后，罐頂和罐底凝油層厚度達(dá)到最大，均為油罐液高。具體分析可知，初始時(shí)刻，罐底部將形成層狀的油溫分布，如圖5(a)，凝油層出現(xiàn)。隨著罐內(nèi)湍流自然對(duì)流的形成，罐底凝油層將受到來(lái)自核心區(qū)含蠟原油的加熱和沖刷，凝油層緩慢融化，溫降45 h后，罐底凝油層消失。隨著溫降過(guò)程的繼續(xù)進(jìn)行，罐內(nèi)油溫逐漸降低，罐底和罐頂凝油層又相繼出現(xiàn)，且快速增長(zhǎng)。其中，罐底是罐內(nèi)油溫最低的區(qū)域，且傳熱方式以導(dǎo)熱為主，因此罐底部凝油層出現(xiàn)相對(duì)較早，且增長(zhǎng)緩慢。而罐頂部湍流自然對(duì)流過(guò)程比較劇烈，含蠟原油損失的熱量能快速?gòu)挠凸藓诵膮^(qū)得到補(bǔ)充。因此，罐頂部凝油層出現(xiàn)相對(duì)較晚，且隨著罐內(nèi)油溫的降低，凝油層將快速增長(zhǎng)，如圖8所示。

3.3 單盤式浮頂油罐罐頂、罐底和罐壁處的傳熱特性

3.1節(jié)和3.2節(jié)分別研究了單盤式浮頂油罐內(nèi)含蠟原油的溫降規(guī)律和凝油層增長(zhǎng)規(guī)律，本節(jié)主要研究單盤式浮頂油罐內(nèi)含蠟原油與罐頂、罐底和罐壁鋼板層之間的傳熱特性，其中，傳熱量由式(22)計(jì)算。

方程中，i代表計(jì)算位置編號(hào)；N代表計(jì)算邊界網(wǎng)格總數(shù)；is代表傳熱面積；代表法向溫度梯度。

圖9給出了單盤式浮頂油罐罐頂、罐底和罐壁處傳熱量隨溫降時(shí)間的變化曲線。從圖中可以看出，初始時(shí)刻，單盤式浮頂油罐內(nèi)含蠟原油與外界環(huán)境之間的熱交換主要發(fā)生在罐底部，其中，最大傳熱量達(dá)到約5.5 kW。隨著罐底溫度梯度的形成，罐底傳熱量快速減小。當(dāng)溫降時(shí)間超過(guò)220 h后，罐底部出現(xiàn)了凝油層，傳熱方式由自然對(duì)流轉(zhuǎn)變?yōu)橄灳Ф嗫捉橘|(zhì)傳熱，類似于導(dǎo)熱，傳熱量小于0.2 kW。對(duì)于罐頂部，當(dāng)溫降時(shí)間小于220 h時(shí)，罐頂部以湍流自然對(duì)流形式向外傳熱，且隨著湍流強(qiáng)度的增大，傳熱量緩慢增大，最大傳熱量超過(guò)2.0 kW。隨著溫降過(guò)程的進(jìn)行，罐頂部開(kāi)始出現(xiàn)凝油層，傳熱方式轉(zhuǎn)變?yōu)橄灳Ф嗫捉橘|(zhì)傳熱，傳熱量逐漸減小，最終穩(wěn)定在0.8 kW左右。此外，由于罐壁處包裹有0.1 m厚的保溫層，在整個(gè)溫降過(guò)程中，罐壁處的傳熱量相對(duì)穩(wěn)定，不超過(guò)0.3 kW。

圖6 不同溫降時(shí)刻，罐內(nèi)含蠟原油流場(chǎng)分布Fig. 6 Stream function distribution in the tank at different moments

圖7 罐內(nèi)核心區(qū)油溫和平均油溫變化曲線Fig. 7 The core region temperature and average temperature in the tank

綜上所述，對(duì)于單盤式浮頂油罐，在罐壁保溫層作用下，罐壁處傳熱過(guò)程相對(duì)穩(wěn)定，傳熱量較小。相對(duì)而言，罐頂和罐底傳熱量較大，且變化過(guò)程比較復(fù)雜。在短期儲(chǔ)存時(shí)，罐頂和罐底部是主要的傳熱區(qū)域；而在長(zhǎng)期儲(chǔ)存時(shí)，罐頂是最主要的傳熱區(qū)域。因此，在單盤式浮頂油罐保溫設(shè)計(jì)中，要重點(diǎn)關(guān)注罐頂和罐底部。

圖8 罐頂和罐底凝油層的增長(zhǎng)Fig. 8 Growth of gel oil at the bottom and top of the tank

4 結(jié)論

基于大渦模擬方法，本文建立了考慮含蠟原油非牛頓性和析蠟相變過(guò)程的單盤式浮頂油罐內(nèi)含蠟原油湍流溫降物理數(shù)學(xué)模型，并發(fā)展了一體化耦合求解技術(shù)。采用該模型，本文對(duì)實(shí)際1 000方單盤式浮頂油罐內(nèi)含蠟原油溫降過(guò)程進(jìn)行計(jì)算，研究罐內(nèi)含蠟原油溫度場(chǎng)和流場(chǎng)的演化、凝油層增長(zhǎng)以及傳熱規(guī)律，得到以下結(jié)論：

(1)當(dāng)罐內(nèi)含蠟原油還沒(méi)完全膠凝時(shí)，在湍流自然對(duì)流作用下，罐內(nèi)油溫近似均勻，且整體發(fā)生溫降。當(dāng)罐內(nèi)含蠟原油膠凝后，罐內(nèi)傳熱過(guò)程為蠟晶多孔介質(zhì)傳熱，類似于導(dǎo)熱。此時(shí)，從罐頂、罐底和罐壁處傳入油罐的冷量開(kāi)始向油罐核心區(qū)推進(jìn)，油罐中出現(xiàn)了明顯的冷熱油界面。

(2)就凝油層增長(zhǎng)而言，對(duì)于本文算例，溫降初期，罐底部出現(xiàn)了凝油層。然而，隨著罐內(nèi)湍流過(guò)程的形成，凝油層逐漸被加熱和沖刷，最終完全融化。到溫降后期，隨著罐內(nèi)油溫的進(jìn)一步降低，罐頂和罐底再次出現(xiàn)凝油層，且凝油層表現(xiàn)出指數(shù)的、波動(dòng)式增長(zhǎng)的特點(diǎn)。

(3)通過(guò)對(duì)罐內(nèi)傳熱過(guò)程的研究發(fā)現(xiàn)，在罐壁保溫層作用下，罐壁處傳熱過(guò)程相對(duì)穩(wěn)定，傳熱量較小，而罐頂和罐底傳熱量相對(duì)較大，且變化過(guò)程更加復(fù)雜。就短期儲(chǔ)存而言，罐頂和罐底是主要的傳熱區(qū)域；而就長(zhǎng)期儲(chǔ)存而言，罐頂是最主要的傳熱區(qū)域。因此，在單盤式浮頂油罐保溫設(shè)計(jì)中，要重點(diǎn)關(guān)注罐頂和罐底部。

[1] 郭光臣, 董文蘭, 張志廉. 油庫(kù)設(shè)計(jì)與管理[M]. 東營(yíng)： 中國(guó)石油大學(xué)出版社, 2006. [GUO G C, DONG W L, ZHANG Z L. The design and management of tank farm[M]. Dongying： China University of Petroleum Press, 2006.]

[2] 楊筱蘅. 輸油管道設(shè)計(jì)與管理[M]. 東營(yíng)： 中國(guó)石油大學(xué)出版社, 2006. [YANG X H. Oil pipeline design and management[M]. Dongying： China University of Petroleum Press, 2006.]

[3] 于達(dá). 大型浮頂油罐測(cè)溫系統(tǒng)的研發(fā)[J]. 油氣儲(chǔ)運(yùn), 2005, 24(8)： 41-43. [YU D. The development of the oil temperature measured system in large fl oating roof oil tank[J]. Oil and Gas Storage and Transportation, 2005, 24(8)： 41-43.]

[4] 趙志明. 大慶北油庫(kù)浮頂儲(chǔ)油罐非穩(wěn)態(tài)傳熱問(wèn)題的數(shù)值計(jì)算[D]. 大慶： 大慶石油學(xué)院, 2009. [ZHAO Z M. The numerical computation of transient heat transfer problems of the fl oating-roof tank in Daqing N. Tank farm[D]. Daqing： Daqing Petroleum Institute, 2009.]

[5] 李超, 劉人瑋, 李旺等. 大型浮頂儲(chǔ)罐原油溫度場(chǎng)實(shí)驗(yàn)測(cè)試研究[J]. 工程熱物理學(xué)報(bào), 2013, 34(12)： 2 332-2 334. [LI C, LIU R W, LI W, et al. Crude oil temperature measurement in a large-scale fl oating roof tank[J]. Journal of Engineering Thermophysics, 2013, 34(12)： 2 332-2 334.]

[6] LIN W X, ARMFIELD S W. Long-term behavior of cooling fluid in a vertical cylinder[J]. International Journal of Heat and Mass Transfer, 2005, 48： 53-66.

[7] OLIVESKI R D C. Correlation for the cooling process of vertical storage tanks under natural convection for high Prandtl number[J]. International Journal of Heat and Mass Transfer, 2013, 57(1)： 292-298.

[8] OLIVESKI R D C, MACAGNAN M H, COPETTI J B, et al. Natural convection in a tank of oil： Experimental validation of a numerical code with prescribed boundary condition[J]. Experimental Thermal and Fluid Science, 2005, 29(6)： 671-680.

[9] 李旺. 大型浮頂油罐溫度場(chǎng)數(shù)值模擬方法及規(guī)律研究[D]. 北京： 中國(guó)石油大學(xué)(北京), 2013. [LI W. Study on numerical simulation methods and regularities for temperature fi eld of large fl oating roof oil tank[D]. Beijing： China University of Petroleum (Beijing), 2013.]

[10] MATIN M H, POP I, KHANCHEZAR S. Natural convection of power-law fl uid between two-square eccentric duct annuli[J]. Journal of Non-Newtonian Fluid, 2013, 197： 11-23.

[11] TURAN O, SACHDEVA A, CHAKRABORTY N, et al. Laminar natural convection of power-law fl uids in a square enclosure with differentially heated side walls subjected to constant temperatures[J]. Journal of Non-Newtonian Fluid, 2011, 166： 1 049-1 063.

[12] VOLLER V R, PRAKASH C. A fi xed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems[J]. International Journal of Heat and Mass Transfer. 1987, 30(8)： 1 709-1 719.

[13] JONES B J, SUN D, KRISHNAN S, et al. Experimental and numerical study of melting in a cylinder[J]. International Journal of Heat and Mass Transfer. 2006, 49(15-16)： 2 724-2 738.

[14] OMARI K E, KOUSKSOU T, GUER Y L. Impact of shape of container on natural convection and melting inside enclosures used for passive cooling of electronic devices[J]. Applied Thermal Engineering. 2011, 31(14-15)： 3 022-3 035.

[15] 張兆順, 崔貴香, 徐春曉. 湍流大渦數(shù)值模擬的理論與應(yīng)用[M]. 北京： 清華大學(xué)出版社, 2008. [ZHANG Z S, CUI G X, XU C X. Theory and application of Large Eddy Simulation[M]. Beijing： Tsinghua University Press, 2008.]

[16] ANSYS FLUENT Theory Guide[M]. ANSYS Inc., 2011.

[17] 袁世偉. 冪律非牛頓流體流動(dòng)的數(shù)值計(jì)算與實(shí)驗(yàn)研究[D]. 上海： 華東理工大學(xué), 2014. [YUAN S W. Numerical simulation andexperimental study of power-law fl uid[D]. Shanghai： East China University of Science and Technology, 2014.]

[18] WANG M, YU G J, ZHANG X Y, et al. Numerical investigation of melting of the waxy crude oil in an oil tank[J]. Applied Thermal Engineering. 2017, 115： 81-90.

[19] JASAK H, WELLER H G, GOSMAN A D. High resolution NVD differencing scheme for arbitrarily unstructured meshes[J]. International Journal for Numerical Methods in Fluids. 1998, 31(2)： 431-449.

[20] 陶文銓. 計(jì)算傳熱學(xué)的近代進(jìn)展[M]. 北京： 科學(xué)出版社, 2001. [TAO W Q. Recent advances in computational heat transfer[M]. Beijing： Science Press, 2001.]

[21] AMPOFO F, KARAYIANNIS T G. Experimental benchmark data for turbulent natural convection in an air filled square cavity[J]. International Journal of Heat and Mass Transfer. 2003, 46(19)： 3 551-3 572.

[22] KOWALCZYK W, HARTMANN C, DELGADO A. Modeling and numerical simulation of convection driven high pressure induced phase change[J]. International Journal of Heat and Mass Transfer. 2004, 47(5)： 1 079-1 089.

Numerical study on the temperature drop characteristics of waxy crude oil in a single-plate fl oating roof oil tank

WANG Min1, LI Jingfa1, ZHANG Xinyu2, YU Bo3
1 National Engineering Laboratory for Pipeline Safety/Beijing Key Laboratory of Urban Oil and Gas Distribution Technology/ China University of Petroleum-Beijing, Beijing 102249, China 2 Sinopec International Petroleum Exploration and Production Corporation, Beijing, 100029 China 3 School of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China

Physical and mathematical models for the temperature drop process of the waxy crude oil in the single-plate fl oating roof oil tank are established with the consideration of non-Newtonian behavior and wax precipitation, and a coupled integrative numerical procedure is developed. In this research, the non-Newtonian behavior is described by the power-law equation. The turbulent fl ow is calculated by Large Eddy Simulation (LES) method. Wax precipitation of the waxy crude oil in the tank is simulated by the enthalpy-porous media theory, in which the gel oil interface is tracked. The numerical program is validated by the results obtained from the literatures. Based on the verif i ed program, temperature drop process in a single-plate fl oating roof oil tank is calculated, and the evolution characteristics of the waxy crude oil in the tank are studied. Furthermore, gel oil growth on the tank top and tank bottom and heat fl ux on tank top, tank bottom and tank wall are also investigated in this research. The research results provide guidance for the scientif i c designing of the single-plate fl oating roof oil tank and making schedule of waxy crude oil turnover reasonably.

single-plate fl oating roof oil tank; temperature drop characteristics; non-newtonian behavior; phase change; LES

10.3969/j.issn.2096-1693.2017.02.025

(編輯 馬桂霞)

王敏, 李敬法, 張欣雨, 宇波. 單盤式浮頂油罐內(nèi)含蠟原油溫降規(guī)律數(shù)值計(jì)算研究. 石油科學(xué)通報(bào), 2017, 02： 267-278

WANG Min, LI Jingfa, ZHANG Xinyu, YU Bo. Numerical study on the temperature drop characteristics of waxy crude oil in a single-plate fl oating roof oil tank. Petroleum Science Bulletin, 2017, 02： 267-278. doi： 10.3969/j.issn.2096-1693.2017.02.025

*通信作者, yubobox@vip.163.com

2017-03-15

國(guó)家自然科學(xué)基金(No. 51325603)資助