基于概率有限元的氣缸蓋疲勞可靠性分析

吳波， 秦新鋒， 賈曉亮， 鄧雅沖

(1. 中國北方發(fā)動機研究所(天津)， 天津 300400； 2. 北京理工大學機械與車輛學院， 北京 100081;3. 中國人民解放軍駐616廠軍事代表室， 山西 大同 037036； 4. 中國人民解放軍陸軍裝甲軍代局駐天津軍代室， 天津 300400)

?

基于概率有限元的氣缸蓋疲勞可靠性分析

吳波1，2， 秦新鋒3， 賈曉亮3， 鄧雅沖4

(1. 中國北方發(fā)動機研究所(天津)， 天津 300400； 2. 北京理工大學機械與車輛學院， 北京 100081;3. 中國人民解放軍駐616廠軍事代表室， 山西 大同 037036； 4. 中國人民解放軍陸軍裝甲軍代局駐天津軍代室， 天津 300400)

提出了一種基于均勻試驗設計和BP神經(jīng)網(wǎng)絡模型構建隨機參數(shù)與結構響應之間的近似非線性關系的概率有限元方法，該方法較直接Monte-Carlo法需要的樣本數(shù)據(jù)大幅減少，更適合大規(guī)模計算的結構概率有限元分析。采用該方法以某型柴油機氣缸蓋結構疲勞失效分析為算例，進行了可靠度期望壽命計算，并通過對影響氣缸蓋應力的燃燒壓力、各螺栓預緊力和噴油器壓緊力等22個載荷參數(shù)的均值和標準差的敏感性分析，初步確定了造成氣缸蓋本體結構疲勞開裂的主要影響因素。

概率有限元； 柴油機； 氣缸蓋； 結構疲勞； 可靠性

發(fā)動機氣缸蓋的主要作用是密封氣缸，一方面通過火焰板與氣缸套和活塞構成燃燒室，承受高溫高壓的燃氣作用，另一方面通過進排氣道和氣門組織新鮮空氣進入燃燒室并將廢氣排出燃燒室。同時為了保證缸蓋和氣缸套之間的密封，氣缸蓋還要受到很大的螺栓預緊力的作用[1]。發(fā)動機是熱動力機械，在其運行過程中，氣缸蓋受到熱負荷和機械載荷的雙重作用，各部分的溫度分布很不均勻且溫差很大，本體結構承受著很大的熱-機耦合應力，是發(fā)動機中最易發(fā)生故障的部件之一[2-3]。當前為了滿足世界各國越來越嚴格的排放法規(guī)，實現(xiàn)節(jié)能、減排和輕量化設計目標，高強化燃燒、渦輪增壓和高承載鋁質(zhì)氣缸蓋等技術在現(xiàn)代發(fā)動機設計中被廣泛采用，發(fā)動機的強化程度越來越高[4]。在強化程度較低的情況下，可以采用較大的安全系數(shù)來保證氣缸蓋的可靠性，但是隨著發(fā)動機強化程度的不斷提高，氣缸蓋的熱機負荷已經(jīng)接近常規(guī)設計結構的使用極限，結構設計的安全裕度不可避免地越來越低。若再不考慮載荷、機械性能和結構幾何尺寸等分散性的影響，對氣缸蓋在各種使用工況下的疲勞壽命進行精確評估和設計，將無法保證高強化發(fā)動機氣缸蓋的疲勞耐久性和可靠性。

概率有限元法的最初思路是Monte-Carlo法與有限元法直接結合，可稱為直接Monte-Carlo法[5]。由于常規(guī)的直接Monte-Carlo法是建立在大量確定性有限元計算的基礎上，一般至少需要幾千個樣本點，特別是對于發(fā)動機氣缸蓋這種單元數(shù)量規(guī)模較大，且需要進行熱機耦合計算的結構其計算量極大，在現(xiàn)有計算技術條件下采用直接Monte-Carlo法無法滿足工程需求。因此，本研究以某型柴油機氣缸蓋為范例，提出了一種基于均勻試驗設計的概率有限元氣缸蓋疲勞可靠性分析方法，首先在設計區(qū)域內(nèi)對影響氣缸應力的各變量(材料、載荷等)進行均勻試驗設計，通過Abaqus確定性仿真得到各組均勻試驗設計參數(shù)的響應值，采用Matlab中的BP神經(jīng)網(wǎng)絡對均勻試驗設計的樣本與響應值進行非線性回歸分析；再利用Nessus可靠性分析軟件按解析法、近似模型法或抽樣法產(chǎn)生隨機模型需要的材料、載荷、邊界條件等隨機變量的樣本值，并將這些隨機變量值映射到Matlab的腳本文件中，通過非線性插值的方法獲取各隨機變量在其他組合形式下結構的動態(tài)響應值，進而通過S-N曲線計算氣缸蓋結構的疲勞可靠度期望壽命，并對影響氣缸蓋可靠度期望壽命的主要參數(shù)開展靈敏度分析。

1 引入隨機性影響的氣缸蓋應力響應計算

1.1 氣缸蓋關鍵部位應力影響因素及其隨機性分析

在機械可靠性設計中，影響結構件應力分布的物理參數(shù)、幾何參數(shù)等設計變量較多。一般認為，在機械可靠性設計中，所有這些設計參數(shù)都是隨機變量，它們應該是經(jīng)過多次試驗測定的實際數(shù)據(jù)并經(jīng)過統(tǒng)計檢驗后得到的統(tǒng)計量。而目前關于這些設計參數(shù)的統(tǒng)計數(shù)據(jù)、分布形式等資料很缺乏，特別是與溫度相關的設計參數(shù)統(tǒng)計數(shù)據(jù)更是匱乏，而且如果引入熱機耦合疲勞分析，概率有限元可靠性分析的計算量也將非常巨大。因此在本次案例分析中，僅以某三缸一蓋整體式柴油機氣缸蓋在試驗載荷作用下的結構可靠性分析作為一個范例，根據(jù)影響氣缸蓋機械應力設計參數(shù)的實測值和設計公差分布情況，作適當?shù)募僭O和簡化處理，暫沒有考慮溫度相關的計算參數(shù)的分散性。建立的有限元計算模型見圖1。

重點引入了對氣缸蓋水腔壁、中隔板和進排氣道等關鍵部位應力響應影響顯著的幾個因素的隨機分布特性，即燃燒壓力和各螺栓的預緊力等22個參數(shù)，計算該型氣缸蓋在350h考核工況僅機械載荷作用下的疲勞壽命的累積分布和可靠期望壽命。

a) 作用于氣缸蓋火力面的燃燒壓力P=12.8 MPa，其波動范圍在(12.8±0.85) MPa之間；

b) 氣缸蓋螺栓預緊力，其中強力絲對螺栓8個，縫合絲對螺栓12個，二者螺栓預緊力分別為T=107.2 kN和TT=49 kN，預緊力波動范圍分別為(107.2±4.2) kN和(49±0.65) kN；

c) 噴油器安裝預緊力YT波動范圍在(16±0.13) kN。

圖1 氣缸蓋有限元計算模型

考慮各參數(shù)在制造裝配和工作過程中的隨機性，假設都是服從截尾正態(tài)分布的隨機變量，其分布類型和參數(shù)見表1。

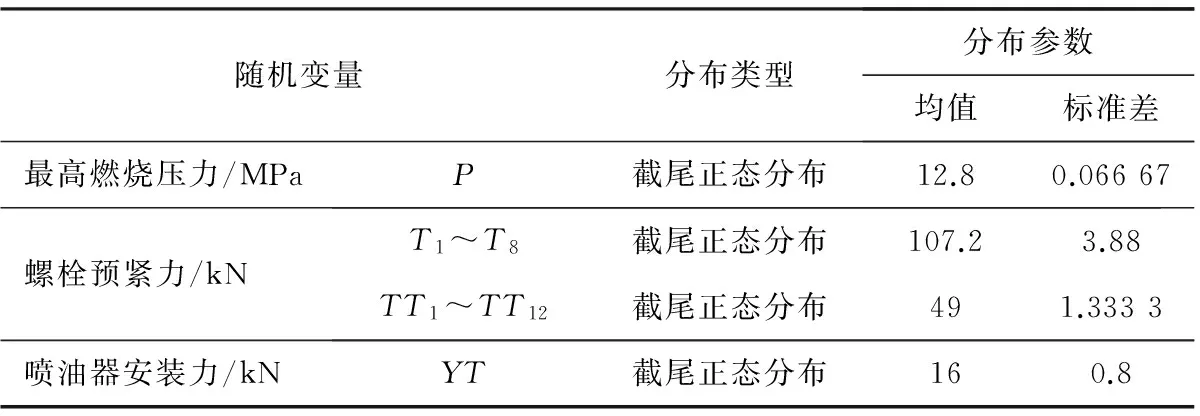
表1 各隨機變量分布類型與參數(shù)

1.2 引入隨機性影響的缸蓋關鍵部位應力響應計算

由于氣缸蓋熱機耦合應力的有限元計算十分耗時，完成一次完整的計算過程需要2.5～4 h，因此在進行結構可靠性分析計算時，若采用概率有限元中常規(guī)的蒙特卡洛(Monte-Carlo)抽樣模擬方法，其時間成本是不可估量和難以承受的。因此,本實例提出了采用均勻試驗設計的方法和BP神經(jīng)網(wǎng)絡模型來構建氣缸蓋有限元模型中隨機參數(shù)與結構響應之間的近似模型。均勻試驗設計是為了樣本點在試驗設計空間充分均勻分布，BP神經(jīng)網(wǎng)絡模型是為了構建隨機參數(shù)與結構響應之間的近似非線性關系。這樣做的另外一個好處是，按照均勻試驗設計做的試驗，其樣本在空間中充分均勻分散，且仿真結果保存在本地硬盤中，可提取的結果較豐富，不僅僅用于疲勞分析，還可用于變形、斷裂、熱力學的可靠性分析，可有效減少仿真所需要的時間。

1.2.1 氣缸蓋隨機參數(shù)的均勻試驗設計

均勻試驗設計的基本想法是要使試驗點在因子空間中具有較好的均勻分散性，其本質(zhì)內(nèi)容是從少量試驗結果中獲取帶規(guī)律性的結果，也可進行回歸分析。求均勻設計是一個優(yōu)化問題，由于求解是在一個離散的空間上，目標函數(shù)的連續(xù)性和可微性已失去意義，從而傳統(tǒng)的各種優(yōu)化方法失去了效力。本研究采用好格子點法(good lattice point)構造均勻設計表，其方法如下[6]：

1) 給定試驗數(shù)n，尋找比n小的整數(shù)h，且使n和h的最大公約數(shù)為1。符合這些條件的正整數(shù)組成向量h=(h1，h2，…h(huán)m)，其中m由歐拉函數(shù)φ(n)決定。

2) 均勻設計表的第j列按照下法生成

uij=ihj[modn]。

(1)

這里[modn]表示同余運算，若ihj超過n，則用它減去n的一個適當倍數(shù)，使差落在[1，n]之中。uij可以遞推來生成(其中i=1，…n-1)，

u1,j=hj，

(2)

(3)

1.2.2 氣缸蓋應力響應的BP神經(jīng)網(wǎng)絡模型

本實例的復雜程度使得必須要借助有限元方法的數(shù)值方法來解決問題，因得不到響應的顯示表達式，所以在求解可靠性靈敏度時比采用一般方法要困難許多，不僅耗時，而且還不容易得到滿意的結果。為此，可利用BP神經(jīng)網(wǎng)絡模型來建立隨機響應和隨機變量之間的非線性映射關系(見圖2)。

圖2 BP網(wǎng)絡結構示意

利用BP神經(jīng)網(wǎng)絡模型來建立隨機響應u和隨機變量B={bi}T={b1，b2，…bn}T之間的非線性映射關系，將有限元分析計算得到的樣本作為BP神經(jīng)網(wǎng)絡的訓練樣本。采用包含一個隱含層的BP神經(jīng)網(wǎng)絡模型，隱含層采用log-sigmoid的S型傳遞函數(shù)，輸出層采用purelin的線性傳遞函數(shù)，BP神經(jīng)網(wǎng)絡的數(shù)學模型為[7]

(4)

式中：n為輸入層節(jié)點數(shù);ωji為輸入層與隱含層之間的權值；θj為輸入層與隱含層的閾值；m為隱含層的節(jié)點數(shù)；ωkj為隱含層與輸出層之間的權值；θk為隱含層與輸出層之間的閾值。隱含層的傳遞函數(shù)δ(·)一般采用logsig函數(shù)，輸出層采用purelin的線性傳遞函數(shù)，訓練函數(shù)可選用BP動量算法traingdm函數(shù)，這種方法所加入的動量項實質(zhì)上相當于阻尼項，它減少了學習過程的振蕩趨勢，從而改善了網(wǎng)絡擬合的收斂性。

1.2.3 氣缸蓋疲勞開裂危險部位應力響應計算

柴油機試驗現(xiàn)場測試結果顯示，在標定功率條件下氣缸蓋承受的最高燃燒壓力基本在12.8MPa附近，沒有發(fā)生較大的波動，因此在計算中氣缸蓋載荷簡化為均值12.8MPa，標準差為0.066 67MPa。氣缸蓋溫度場則按照標定功率下的計算參數(shù)進行擬合計算，并通過單缸機測溫試驗結果進行修正，本算例中暫不考慮溫度場計算參數(shù)的隨機性影響。要獲得上述工況的氣缸蓋開裂危險部位應力響應，首先采用式(1)至式(3)給出的均勻化試驗設計方法對柴油機標定工況的燃燒壓力和各螺栓的預緊力等22個參數(shù)進行均勻化試驗設計，本例中共設計了50組參數(shù)，并作為有限元計算的輸入值進行確定性的氣缸蓋應力響應計算。從得到的50組氣缸蓋應力響應計算結果中分別提取氣缸蓋本體開裂危險部位(見圖3中1，2位置處)的應力值，50組應力響應結果尚不能完整反映表1中22個隨機變量的影響，還需要結合Matlab中的BP神經(jīng)網(wǎng)絡，即式(4)對均勻試驗設計的樣本與危險部位應力響應值進行非線性回歸分析，再利用Nessus軟件按解析法、近似模型法或抽樣法產(chǎn)生本算例隨機模型需要的材料、載荷、邊界條件等隨機變量的樣本值，并將這些隨機變量值映射到Matlab的腳本文件中，通過非線性插值的方法獲取各隨機變量(材料特性、載荷特性等)在其他組合形式下的氣缸蓋疲勞失效薄弱部位第一主應力的動態(tài)響應值。

圖3 氣缸蓋本體開裂危險部位示意

2 氣缸蓋可靠壽命及敏感性分析

Nessus支持的響應模型可以是數(shù)值模型、回歸模型或預定義的模型，支持的數(shù)值模型可以是通用有限元軟件模型，如Ansys，Abaqus，MSCNastran等，或自定義模型。本案例采用自定義響應模型[8]，將采用Matlab中的BP神經(jīng)網(wǎng)絡計算的每一組氣缸蓋疲勞失效薄弱部位(考察點)的第一主應力循環(huán)響應值進行提取，并進行最大應力和最小應力計算，采用公式(5)進行平均應力修正，最后結合氣缸蓋材料屬性利用公式(6)進行疲勞壽命計算。

(5)

(6)

式中：σa0為修正后平均應力為0的應力幅值；σa為考察點應力幅值計算值；σm為考察點平均應力計算值；Nf為疲勞壽命值。結合氣缸蓋本體解剖材料的測試數(shù)據(jù)得出抗拉強度σb=254 MPa，疲勞強度指數(shù)b=-0.124，疲勞強度系數(shù)σf'=359.05。

指定Nessus的概率分析類型為“累積概率分布分析(Full cumulative distribution)”，即結構疲勞壽命的累積分布，分析方法選擇全局高效算法(EGRA)[9]。計算獲得的12.8 MPa工況下氣缸蓋本體疲勞開裂最危險部位(圖3中1點)的疲勞壽命累積分布見圖4。在可靠度為90%時，經(jīng)計算得出氣缸蓋疲勞危險部位1點的可靠期望壽命為8.378 44×106次載荷循環(huán)，按照該機型標定功率轉(zhuǎn)速2 200 r/min計算約為127 h。

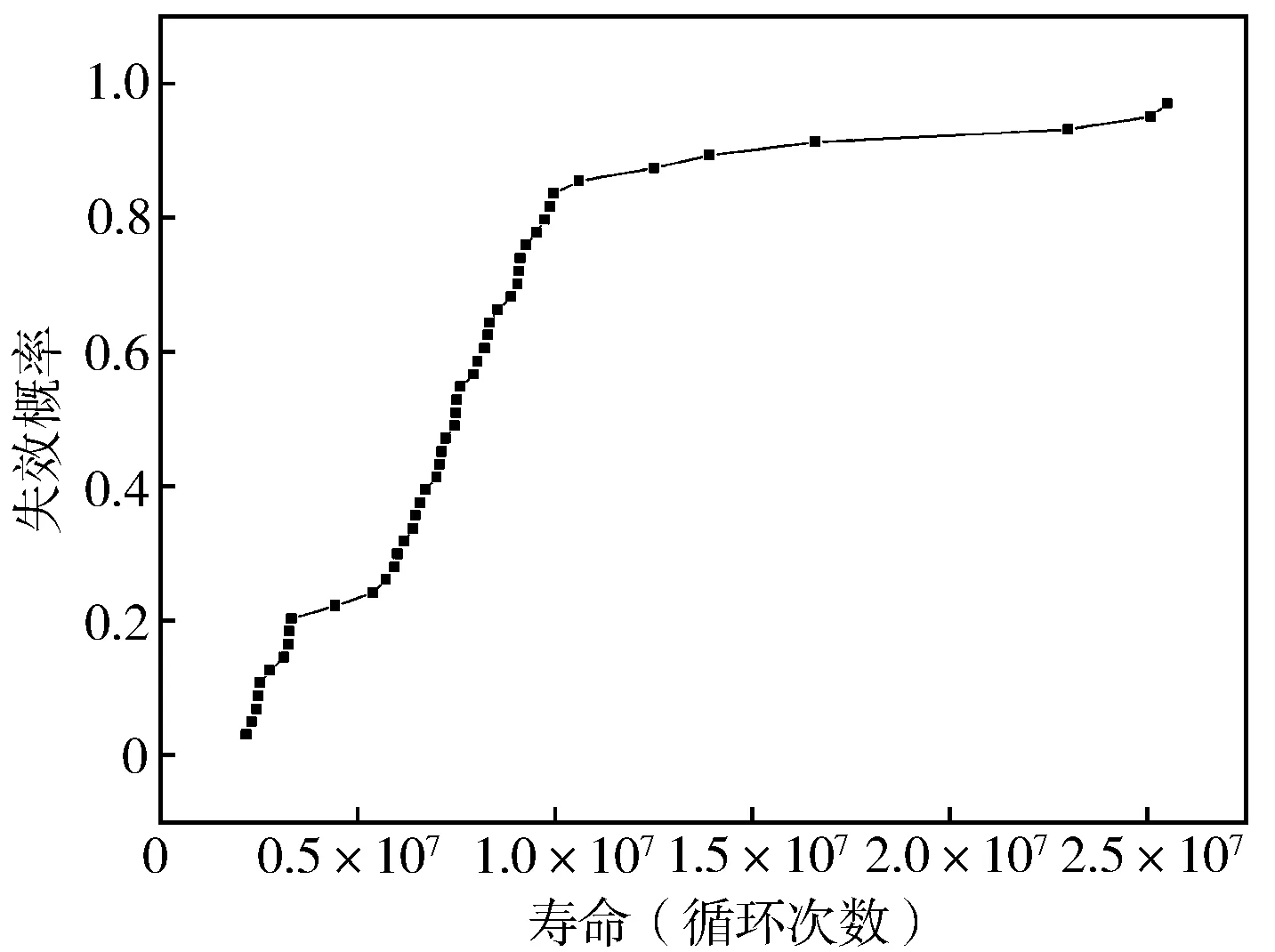
圖4 氣缸蓋本體開裂危險部位疲勞壽命累積分布

本次評估的氣缸蓋兩個疲勞危險部位壽命期望值處失效概率主要影響因素的靈敏度分析見圖5和圖6。

由圖5可見，在期望壽命處，在影響氣缸蓋考察點1處失效概率的22個載荷參數(shù)中，最高燃燒壓力P的均值，噴油器襯套安裝預緊力YT的均值，以及1點所處氣缸的強力絲對螺栓T5～T8預緊力均值，縫合絲對螺栓TT9～TT12預緊力均值對考察點1處的失效影響較大。特別是靠近考察點1的縫合絲對螺栓TT12的預緊力均值影響最為顯著，其次是其對角布置的縫合絲對螺栓TT9預緊力均值。從代表載荷參數(shù)分散性的標準差靈敏度結果來看，噴油器襯套安裝預緊力YT、強力絲對T4、縫合絲對TT4和TT11的影響較強。因此，想要減小考察點1處的失效概率，要盡量降低螺栓的預緊力、最高燃燒壓力和噴油器襯套安裝預緊力均值，并對噴油器襯套安裝預緊力和相關螺栓預緊力的分散性進行嚴格控制。

由圖6可見，在期望壽命處，噴油器襯套安裝預緊力均值對氣缸蓋考察點2處的失效影響非常顯著，強力絲對螺栓T8和縫合絲對螺栓TT7預緊力均值也有較大影響。同時分析結果顯示適當增加縫合絲對螺栓TT9和TT11的預緊力均值則會降低考察點2處的失效概率。

圖5 考察點1失效概率靈敏度分析

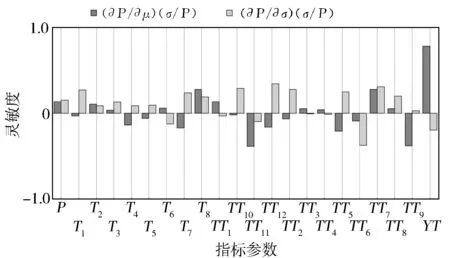
圖6 考察點2失效概率靈敏度分析

3 結束語

本研究提出了一種基于均勻試驗設計的概率有限元疲勞可靠性分析方法，通過BP神經(jīng)網(wǎng)絡模型來構建結構有限元模型中隨機參數(shù)與結構響應之間的近似模型，較直接Monte-Carlo法可大幅減少計算規(guī)模，為采用概率有限元法解決實際工程問題提出了新思路。

采用該方法進行的某型柴油機氣缸蓋可靠壽命分析案例顯示，該方法能夠?qū)α悴考谑У谋姸嗖淮_定性因素進行定量的敏感性分析，確定主要的影響因素，并能夠指出各影響因素的均值和分散性對結構失效的影響關系。

由于影響氣缸蓋疲勞失效的因素眾多，本研究算例僅對影響其疲勞失效的載荷因素隨機性進行了概率有限元計算分析，其他影響因素進行了確定性假設。進一步還需要涵蓋更多影響因素，如溫度場相關參數(shù)和材料性能相關參數(shù)的隨機性等。

[1]WhitelawJH,PayfiF,DesantesJM．Thermo-andfluid-dynamicprocessesindieselengines[M]．Berlin：Springer-Verlag，2002.

[2] 吳波，王增全，解志民，等. 高強化蠕鐵氣缸蓋熱強度的分析與評價[J].汽車工程，2016,38(5):646-651.

[3] 郭良平,張衛(wèi)正,王長園,等.柴油機氣缸蓋傳熱規(guī)律研究[J].北京理工大學學報,2011,31(3):277-282.

[4] 王宇,白敏麗,呂繼組,等.利用部件整體耦合法分析柴油機氣缸蓋熱機械強度[J].內(nèi)燃機工程，2007,28(6):41-48.

[5] 徐鐘濟.蒙特卡羅法[M].上海:上海科學技術出版社,1985:326-332.

[6] 王繼勇,李助軍,劉曉婧,等.均勻試驗設計方法在柴油機多變量優(yōu)化中的應用[J].裝備制造技術,2006(1):6-8.

[7] 鄒亮,汪國強.均勻試驗設計在遺傳算法中的應用[J].華南理工大學學報(自然科學版),2003,31(5):90-92.

[8]NESSUSTheoreticalManual[M].[S.l.]：SouthwestResearchInstitute,2013.

[9]RackwitzR,FiesslerB.Structuralreliabilityundercom-binedloadsequences[J].JournalofComputersandStructures,1978(9):484-494.

[編輯： 潘麗麗]

FatigueReliabilityAnalysisofCylinderHeadBasedonProbabilityFiniteElementMethod

WUBo1,2,QINXinfeng3,JIAXiaoliang3,DENGYachong4

(1.ChinaNorthEngineResearchInstitute(Tianjin),Tianjin300400,China；2.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081,China; 3.MilitaryRepresentativeofficeoftheChinesePeople’sLiberationArmyin616Factory,Datong037036,China;4.MilitaryRepresentativeofficeoftheChinesePeople’sLiberationArmyArmoredTroops,Tianjin300400,China)

A probability finite element method used to construct the approximate nonlinear relation between random parameters and structure responds was supposed based on uniform design and BP neural network. Compared with direct Monte-Carlo method, this method reduced sampled data greatly and was better to apply to the large-scale engineering structure probability finite element calculation. Fatigue failure case of diesel engine cylinder head was carried out by this method. The fatigue reliability life was calculated and the sensitivity analysis of 22 loading parameters such as burning pressure, bolts pre-loading and fuel injector pre-loading was performed too. The main influencing parameters which caused cylinder head structure fatigue failure were determined preliminarily in the end.

probability finite element; diesel engine; cylinder head; structure fatigue； reliability

2017-02-12；

2017-04-10

天津市企業(yè)博士后創(chuàng)新項目擇優(yōu)資助計劃資助項目

吳波(1978—)，男，研究員，博士，主要研究方向為發(fā)動機結構疲勞與可靠性；wubo-cneri@163.com。

10.3969/j.issn.1001-2222.2017.03.006

TK423.32

B

1001-2222(2017)03-0033-05