基于材料循環RVE的I型橢圓裂紋疲勞擴展理論模型研究

石凱凱， 鄭斌

(中國核動力研究設計院核反應堆系統設計技術重點實驗室， 成都610213)

基于材料循環RVE的I型橢圓裂紋疲勞擴展理論模型研究

石凱凱， 鄭斌

(中國核動力研究設計院核反應堆系統設計技術重點實驗室， 成都610213)

基于材料循環RVE和平面應力裂紋尖端循環塑性區內的塑性應變能，建立了I型穿透裂紋的疲勞擴展速率SHI-CAI模型。結合7075-T6材料和結構裂紋前緣疲勞擴展最小壽命假定，研究遠端拉伸板中半橢圓表面裂紋的疲勞擴展規律，并進行了試驗驗證。結果表明，結構裂紋前緣疲勞擴展最小壽命假定可用于描述了I型穿透裂紋和結構裂紋疲勞擴展之間的聯系。最后結合所提出的結構裂紋疲勞擴展理論模型，研究了遠端拉伸板中半橢圓裂紋和橢圓嵌入裂紋的疲勞擴展規律。

循環RVE;I型橢圓裂紋;疲勞裂紋擴展;塑性應變能;理論模型;7075-T6鋁合金

引言

在航空、高鐵等行業，結構裂紋的疲勞擴展直接影響到部件的剩余壽命和剩余強度，因此一直是安全部門關注的要點。眾所周知，含缺陷構件在往復載荷作用下，其裂紋尖端受尖端驅動力的作用，裂紋將發生疲勞擴展。線彈性斷裂力學認為，致使裂紋尖端疲勞擴展的驅動力即為應力強度因子[1]，目前均是通過建立裂紋尖端應力強度因子與裂紋擴展速率之間的聯系來定量描述裂紋的疲勞擴展規律的，如Paris律[2]。

SHI-CAI模型[3]是基于材料裂紋尖端循環RVE和塑性應變能耗散，用來建立材料低周疲勞和I型裂紋擴展速率之間的聯系，同時描述了平面應力條件下I型貫穿裂紋的疲勞裂紋擴展速率。為避免I型裂紋尖端的奇異場，SHI-CAI模型首先在裂紋尖端引入了鈍化方程；其次考慮平面應力裂紋尖端循環塑性區內彈性應變遠小于塑性應變，因此忽略裂紋尖端的彈性應變；然后考慮裂紋尖端循環塑性區范圍內的塑性應變能耗散，并基于材料循環RVE建立了材料低周疲勞(LCF)與I型貫穿裂紋疲勞擴展(FCG)之間的聯系。從安全和經濟的角度，已對SHI-CAI模型結合多種金屬材料進行了有效性驗證。

本文結合航空材料7075-T6鋁合金[4]進一步對SHI-CAI模型預測I型貫穿裂紋疲勞擴展速率的有效性進行驗證；之后，以SHI-CAI模型為基礎，結合針對結構裂紋疲勞擴展所提出的裂紋前緣疲勞擴展最小壽命假定，從理論上建立了用于分析結構裂紋疲勞擴展剩余壽命和擴展規律的理論模型；然后并通過7075-T6鋁合金遠端拉伸板中半橢圓表面裂紋擴展試驗數據[5]進行了驗證。結果表明，結構裂紋前緣疲勞擴展最小壽命假定可用于描述了I型穿透裂紋和I型結構裂紋疲勞擴展之間的聯系。最后基于所提出的結構裂紋疲勞擴展理論模型，以7075-T6鋁合金材料的材料數據分別分析了半橢圓表面裂紋和嵌入橢圓裂紋在循環載荷作用下的裂紋擴展規律。

1結構裂紋前緣疲勞擴展最小壽命假定的疲勞擴展理論模型

工程中通常基于探傷等技術手段，獲得在役結構的缺陷尺寸[6]。然而探傷獲得的實際缺陷尺寸并不是規則的幾何構形，理論分析中通常將其處理為規則的幾何構形，如橢圓等。結構裂紋在循環載荷作用下，其裂紋前緣各點在各自位置處的裂紋疲勞擴展驅動力(應力強度因子幅ΔK)控制下發生擴展。

在結構裂紋疲勞擴展理論模型中，由于裂紋前緣擴展的復雜性，故而只分析能表征結構裂紋前緣形貌的特征角度范圍，通常為0°～90°。

結構裂紋前緣疲勞擴展最小壽命假定：在特征角度范圍內，基于SHI-CAI模型和裂紋前緣驅動力分析裂紋前緣各點擴展一步所需要的各自循環壽命，其中分析得到的最小循環壽命即為結構裂紋前緣擴展最小壽命。繼而，在特征角度范圍內控制裂紋前緣各點擴展的控制點擴展步長可通過SHI-CAI模型和結構裂紋前緣擴展最小壽命假定計算得到。最后得到特征角度范圍內發生一步擴展后的裂紋前緣形貌。

基于SHI-CAI模型可得到結構裂紋特征角度范圍內的疲勞裂紋擴展速率表達式為：

(1)

式中，dl為裂紋前緣擴展步長，rc為裂紋尖端循環塑性區尺寸，ρc為裂紋尖端鈍化區尺寸，N*為發生一次擴展所需要的循環壽命。

(2)

(3)

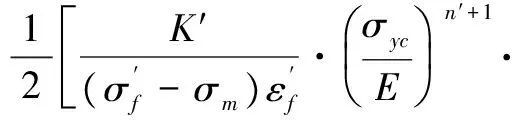
(4)

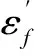
結合SHI-CAI模型和結構裂紋前緣疲勞擴展最小壽命假定，在特征角度范圍內依據控制點擴展量，即可分析I型結構裂紋疲勞擴展規律。

2半橢圓表面裂紋疲勞擴展規律的驗證

在進行結構裂紋疲勞擴展模型建立之前，先結合7075-T6鋁合金的低周疲勞參量，驗證SHI-CAI模型在預測I型貫穿裂紋疲勞擴展速率的有效性。SHI-CAI模型預測結果與試驗數據如圖1所示。表1給出了SHI-CAI模型在分析中所使用到的7075-T6鋁合金相關的半橢圓表面裂紋的幾何尺寸及材料低周疲勞參量。由圖1可知，SHI-CAI模型在分析7075-T6鋁合金的I型貫穿疲勞裂紋擴展穩定階段速率時，其預測結果與實驗結果吻合良好。這為預測I型結構裂紋疲勞擴展提供了必要的基礎數據，同時也驗證了SHI-CAI模型在預測7075-T6鋁合金的裂紋疲勞擴展的有效性。考慮結構裂紋前緣疲勞擴展最小壽命假定，依據SHI-CAI模型的材料循環RVE理論，即可進行I型結構裂紋疲勞擴展規律的研究，繼而分析含缺陷構件的剩余壽命和剩余強度。

圖1I型貫穿疲勞裂紋擴展速率試驗與SHI-CAI模型

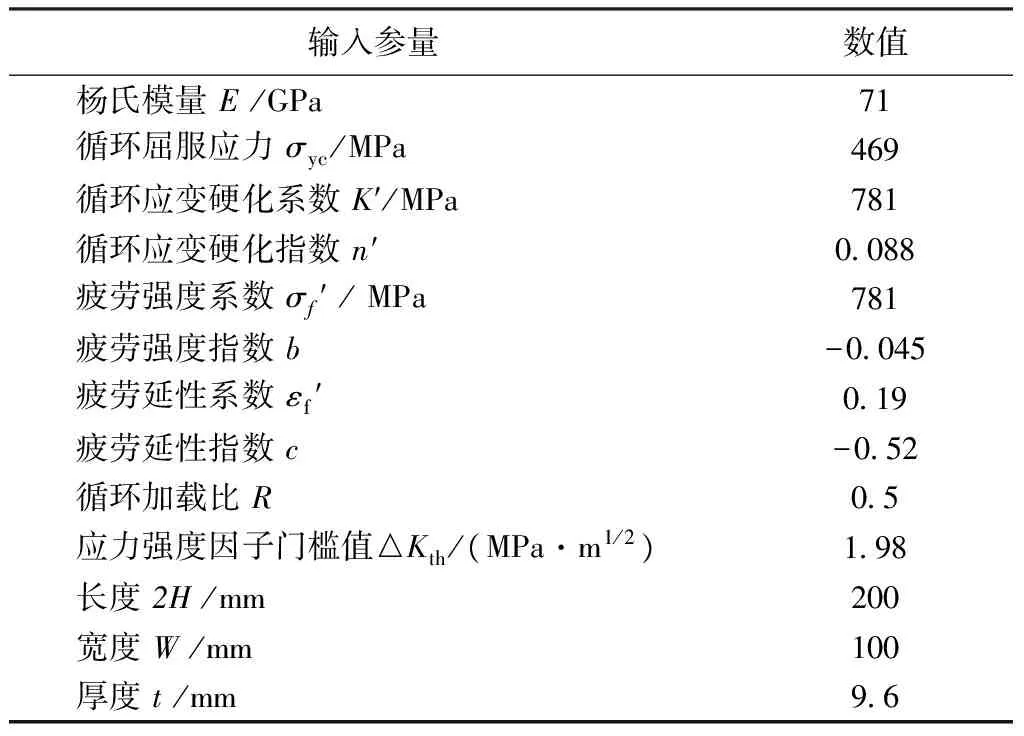
輸入參量數值楊氏模量E/GPa71循環屈服應力σyc/MPa469循環應變硬化系數K′/MPa781循環應變硬化指數n′0 088疲勞強度系數σf′/MPa781疲勞強度指數b-0 045疲勞延性系數εf′0 19疲勞延性指數c-0 52循環加載比R0 5應力強度因子門檻值△Kth/(MPa·m1/2)1 98長度2H/mm200寬度W/mm100厚度t/mm9 6

考慮Newman的遠端拉伸板中半橢圓表面裂紋應力強度因子[7-8]或Hosseini的遠端拉伸板中半橢圓表面裂紋應力強度因子[9]，依據上述理論研究該裂紋疲勞擴展的規律。圖2給出了SHI-CAI模型分析不同初始半橢圓表面裂紋的深度a和表面半長度c之比(α=a/c)隨著半橢圓表面裂紋深度a和板厚度t之比(β=a/t)的形貌變化規律。

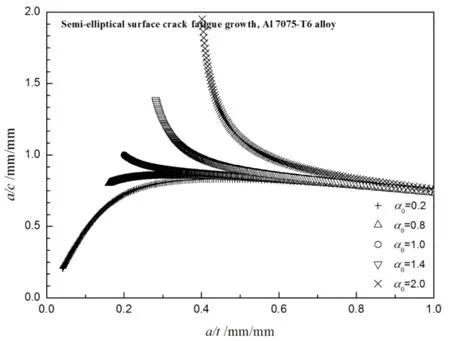
圖2表面半橢圓裂紋形貌變化

YU等[10-11]在考慮等效厚度概念情況下通過有限元研究了半橢圓表面裂紋疲勞擴展壽命和形貌演化，但沒有脫離有限元形成完全的結構裂紋疲勞擴展理論模型。由圖2可知，遠端拉伸板中半橢圓表面裂紋的形貌在遠端循環載荷作用下的曲線變化(即α～β)。當初始形貌為圓形時(即α=1)，其隨著裂紋深度逐漸在板厚度方向上疲勞擴展，裂紋的形貌不在保持圓形，而是趨于一個恒定的α比值，其α約為0.8。

為驗證結構裂紋疲勞擴展最小壽命假定的合理性，需將結構裂紋疲勞擴展理論分析結果與試驗數據進行對比。圖3給出了遠端拉伸板中半橢圓表面裂紋擴展的預測形貌和試驗數據的對比。由圖3可知，基于結構裂紋疲勞擴展最小壽命假定和SHI-CAI模型所建立的預測I型半橢圓表面裂紋疲勞擴展模型，有良好的預測結果，因此可將所提出的結構裂紋疲勞擴展理論模型用于其他I型結構裂紋疲勞擴展的分析中。

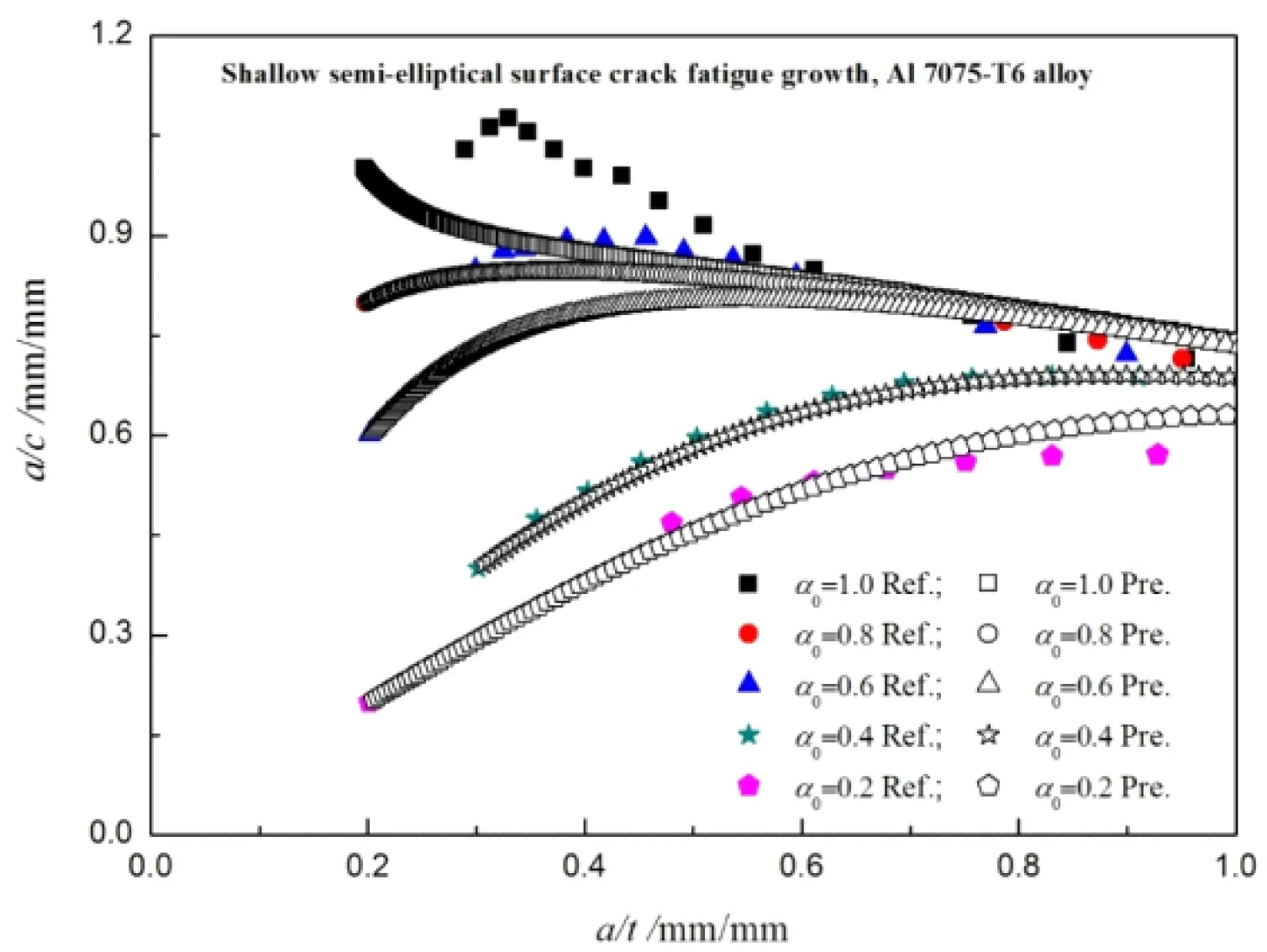
圖3半橢圓表面裂紋疲勞擴展預測結果與試驗對比

3橢圓嵌入裂紋疲勞擴展規律的分析

針對工程中橢圓嵌入裂紋，依據所提出的結構裂紋前緣疲勞擴展最小壽命假定，結合結構裂紋疲勞擴展模型和Newman的遠端拉伸板中橢圓嵌入裂紋應力強度因子[8]，分析了7075-T6鋁合金遠端拉伸板中不同初始形貌的橢圓嵌入裂紋疲勞擴展規律，如圖4所示。

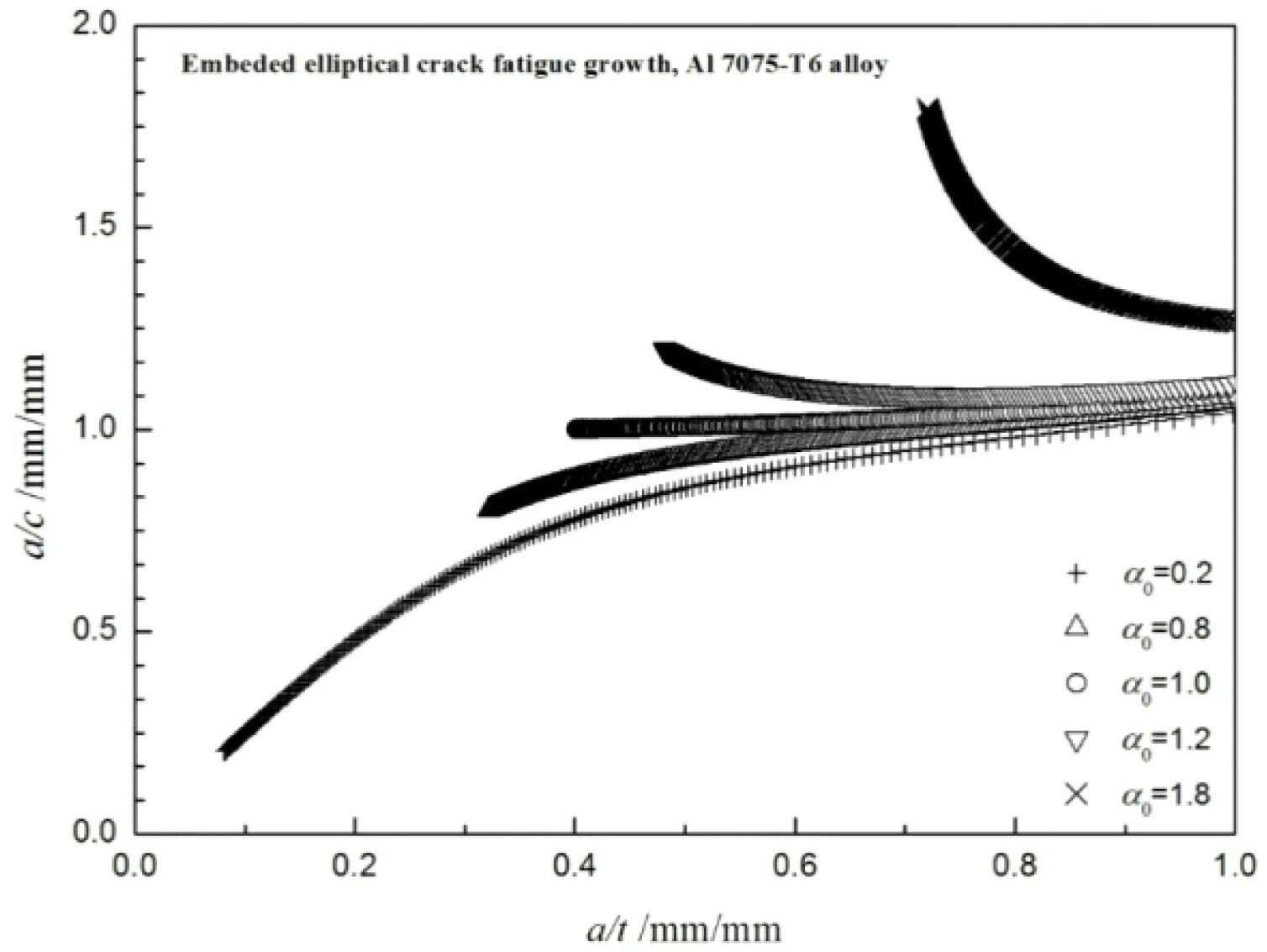
圖4橢圓嵌入裂紋疲勞擴展規律

由圖4可知，當橢圓嵌入裂紋初始形貌是圓形時(即α=1)，在遠端循環載荷作用下發生疲勞擴展。更新后的嵌入裂紋形貌變化不是初始圓形尺寸，而是其α值會變，直至橢圓裂紋穿透板的厚度t。

4結論與展望

結合I型貫穿裂紋疲勞擴展的SHI-CAI模型和結構裂紋疲勞擴展最小壽命假定，建立了預測結構裂紋疲勞擴展的理論模型。通過對7075-T6鋁合金的裂紋疲勞擴展研究，可以得到：

(1) 考慮材料循環RVE的SHI-CAI模型，可用于預測7075-T6鋁合金材料I型裂紋穩定階段的疲勞擴展速率。通過對比試驗數據，可知SHI-CAI模型具有良好的預測效果。

(2) 針對結構裂紋，提出了可用于分析其裂紋疲勞擴展的最小壽命假定。并結合SHI-CAI模型中的循環RVE理論，提出了用于預測I型結構裂紋疲勞擴展的理論模型。

(3) 結合7075-T6鋁合金材料，通過對比遠端拉伸板中半橢圓表面裂紋疲勞擴展試驗數據和結構裂紋疲勞擴展理論模型預測結果，驗證了所提出的預測結構裂紋疲勞擴展理論模型的有效性。

(4) 基于結構裂紋疲勞擴展理論模型，分析分析了遠端拉伸板中半橢圓表面裂紋和橢圓嵌入裂紋疲勞擴展規律。

進一步工作中，可針對工程中其他I型規則結構裂紋或不規則結構裂紋[12]，利用所提出的結構裂紋疲勞擴展理論模型進行剩余壽命和剩余強度的分析；同時結合多種材料試驗數據對結構裂紋疲勞擴展最小壽命假定的合理性進行驗證；或是通過擴展有限元技術[13]分析結構裂紋疲勞擴展，驗證理論模型假定的有效性。

[1] KUJAWSKI D.A new (ΔK+Kmax)0.5 driving force parameter for crack growth in aluminum alloys[J].International Journal of Fatigue,2001,23(8):733-740.

[2] PARIS P,ERDOGAN F.A critical analysis of crack propagation laws[J].Journal of Basic Engineering,1963,85(4):528-533.

[3] SHI K,CAI L,CHEN L,et al.Prediction of fatigue crack growth based on low cycle fatigue properties[J].International Journal of Fatigue,2014,61:220-225.

[4] NOROOZI A,GLINKA G,LAMBERT S.A two parameter driving force for fatigue crack growth analysis[J].International Journal of Fatigue,2005,27(10):1277-1296.

[5] PUTRA I S,SCHIJVE J.Crack opening stress measurements of surface cracks in 7075-T6 aluminium alloy plate specimen through electron fractography[J].Fatigue & Fracture of Engineering Materials & Structures,1992,15(4):323-338.

[6] SHAHJAHAN S,AUBRY A,RUPIN F,et al.Flaw detection on Inconel600? using separation of single and multiple scattering contributions[J].Cancer Imaging the Official Publication of the International Cancer Imaging Society,2012,14(S1):1-2.

[7] NEWMAN J J,RAJU I.An empirical stress-intensity factor equation for the surface crack[J].Engineering Fracture Mechanics,1981,15(1):185-192.

[8] NEWMAN J J,RAJU I.Stress intensity factor equations for cracks in three-dimensional finite bodies[J].ASTM STP,1983,791:238-265.

[9] HOSSEINI A,MAHMOUD M.Evaluation of stress intensity factor and fatigue growth of surface cracks in tension plates[J].Engineering Fracture Mechanics,1985,22(6):957-974.

[10] YU P,GUO W.An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution[J].Engineering Fracture Mechanics,2012,93:65-74.

[11] YU P, SHE C,GUO W.Equivalent thickness conception for corner cracks[J].International Journal of Solids & Structures,2010,47(16):2123-2130.

[12] OORE M,BURNS D.Estimation of stress intensity factors for embedded irregular cracks subjected to arbitrary normal stress fields[J].Journal of Pressure Vessel Technology,1980,102(2):202-211.

[13] PATHAK H,SINGH A,SINGH I V.Fatigue crack growth simulations of 3-D problems using XFEM[J].International Journal of Mechanical Sciences,2013,76(11):112-131.

Theory Model Using Material Cycle RVE for Mode-I Elliptical Crack Fatigue Growth

SHIKaikai,ZHENGBin

(Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute ofChina, Chengdu 610213, China)

Considering the material cycle RVE and the plastic strain energy within the cycle plastic zone near crack tip, the SHI-CAI Model used to analyze the fatigue crack growth rate for mode-I crack is developed. Based on the 7075-T6 alloy and the minimum life of fatigue crack for structural crack front, the semi-elliptical surface crack in a finite plate subjected the remote cycle tension load is studied. At the same time, the theory results are compared with the experiments results for 7075-T6 alloy. The results show that the assumption, the minimum life of fatigue crack growth (MLOFCG) for structural crack front, can be used to describe the relationship between the mode-I crack fatigue growth and the structural crack fatigue growth. At last, the semi-elliptical surface crack and the embedded elliptical crack in a finite plate subjected to the remote cycle tension load are researched based on the fatigue cracking theory model for structural crack.

cycle RVE; mode-I elliptical crack; fatigue crack growth; plastic strain energy; theory model; 7075-T6 Al alloy

2016-12-22

石凱凱(1987-),男,山西曲沃人,博士,主要從事疲勞、損傷和斷裂方面的研究,(E-mail)shikai1000@163.com

1673-1549(2017)03-0041-04

10.11863/j.suse.2017.03.09

TB115

A