BP網(wǎng)絡在進給系統(tǒng)定位誤差預測中的運用

鄧 超， 錢有勝， 吳 軍， 熊 堯， 段超群

(1.華中科技大學機械學院制造裝備數(shù)字化國家工程中心 武漢, 430074)(2.華中科技大學船舶與海洋工程學院 武漢,430074) (3.武漢第二船舶設計研究所 武漢,430070)

?

BP網(wǎng)絡在進給系統(tǒng)定位誤差預測中的運用

鄧 超1， 錢有勝1， 吳 軍2， 熊 堯3， 段超群1

(1.華中科技大學機械學院制造裝備數(shù)字化國家工程中心 武漢, 430074)(2.華中科技大學船舶與海洋工程學院 武漢,430074) (3.武漢第二船舶設計研究所 武漢,430070)

針對機床進給伺服系統(tǒng)定位精度預測的難點，分析了進給伺服系統(tǒng)機械傳動系統(tǒng)定位誤差增長的原因，提出了一種定位誤差預測的方法。在Adams中建立進給伺服系統(tǒng)動力學仿真模型,得到不同初始狀態(tài)下的定位誤差值，基于BP神經(jīng)網(wǎng)絡建立工作臺與螺母座間隙、滾珠絲杠傾斜度、工件負載與定位誤差之間的映射模型，根據(jù)映射模型提出對定位誤差預測的方法。利用所建立的精密運動可靠性試驗平臺進行驗證，證明了該方法的正確性和有效性。

進給伺服系統(tǒng)； BP神經(jīng)網(wǎng)絡； 映射模型； Adams；定位誤差預測

引 言

定位精度是衡量數(shù)控機床性能的重要指標，根據(jù)定位精度可以判斷出機床自動加工過程中能達到的最好的工件加工精度。對機床定位精度預測的研究一直受到眾多學者的關注[1-4]，但是從定位精度退化原因的角度對其進行分析預測的研究較少。定位精度表示理想位置與真實位置的接近程度，能夠通過定位誤差計算得出。定位誤差表示理想位置與真實位置的差值，能夠很好地反映定位精度，易于測量，不需要復雜的數(shù)據(jù)處理過程。筆者在分析定位誤差增長機理的基礎上對其進行預測。

進給伺服系統(tǒng)定位誤差主要取決于性能的優(yōu)劣，受到電氣伺服系統(tǒng)與機械特性參數(shù)的影響，其誤差源包含伺服控制系統(tǒng)、機械傳動系統(tǒng)、環(huán)境負載和加工載荷等。進給伺服系統(tǒng)定位誤差檢測項有軸線定位誤差和機械傳動系統(tǒng)定位誤差，其中軸線定位誤差包括電氣伺服誤差和機械傳動系統(tǒng)誤差。進給伺服系統(tǒng)定位誤差衰退的原因可以分為3類：a.滾珠絲杠材料及尺寸、傳動系統(tǒng)剛度、系統(tǒng)阻尼、工作臺與螺母座間隙、滾珠絲杠傾斜度及工件負載等，稱為結構與工藝參數(shù)；b.各個零部件的磨損、老化、疲勞及彎曲等，稱為故障模式參數(shù)；c.位置環(huán)增益、電流環(huán)增益、速度環(huán)增益及進給率等，稱為控制參數(shù)。滾珠絲杠的磨損會導致工作臺與螺母座間隙增大，滾珠絲杠的彎曲會導致滾珠絲杠傾斜度增大，所以故障模式參數(shù)是通過引起結構與工藝參數(shù)變化而影響定位誤差。結構與工藝參數(shù)中的系統(tǒng)剛度等不會有太大變化，控制參數(shù)主要對電氣伺服誤差產(chǎn)生影響，因而筆者選取結構與工藝參數(shù)中工作臺與螺母座間隙、滾珠絲杠傾斜度及工件負載等，分析這些參數(shù)的變化對進給伺服系統(tǒng)機械傳動系統(tǒng)定位誤差的影響。

機床進給伺服系統(tǒng)結構與工藝參數(shù)的變化一般不容易測得，而現(xiàn)場數(shù)據(jù)收集環(huán)境比較復雜，受到現(xiàn)場加工作業(yè)狀況、場地、操作條件和其他人為因素等方面的影響，因此筆者通過虛擬樣機的方式對結構與工藝參數(shù)、工作臺的輸出進行采樣，并預測定位誤差。

1 機械傳動系統(tǒng)定位誤差增長機理分析

進給伺服系統(tǒng)機械傳動系統(tǒng)是一個二階系統(tǒng)，在擾動輸入為0時，定位誤差不會發(fā)生變化[5],但長時間的磨損會導致機械傳動系統(tǒng)零部件出現(xiàn)間隙、傾斜和彎曲，從而引起定位誤差的增大。因振動、沖擊及工件負載變化對機械傳動系統(tǒng)產(chǎn)生的擾動輸入，也會導致定位誤差的增大。假設聯(lián)軸器之間的間隙、滾珠絲杠與支撐軸承之間的間隙、軸承本身間隙、滾珠絲杠與螺母座之間的間隙等均以工作臺與螺母座間隙α表示，導軌的傾斜度、滾珠絲杠的彎曲度及軸承座的傾斜度等均以滾珠絲杠傾斜度β表示，因振動、沖擊及工件負載變化等引起的擾動輸入以工件負載F表示。機械傳動系統(tǒng)部件與定位誤差之間存在內(nèi)在關系，如圖1所示。

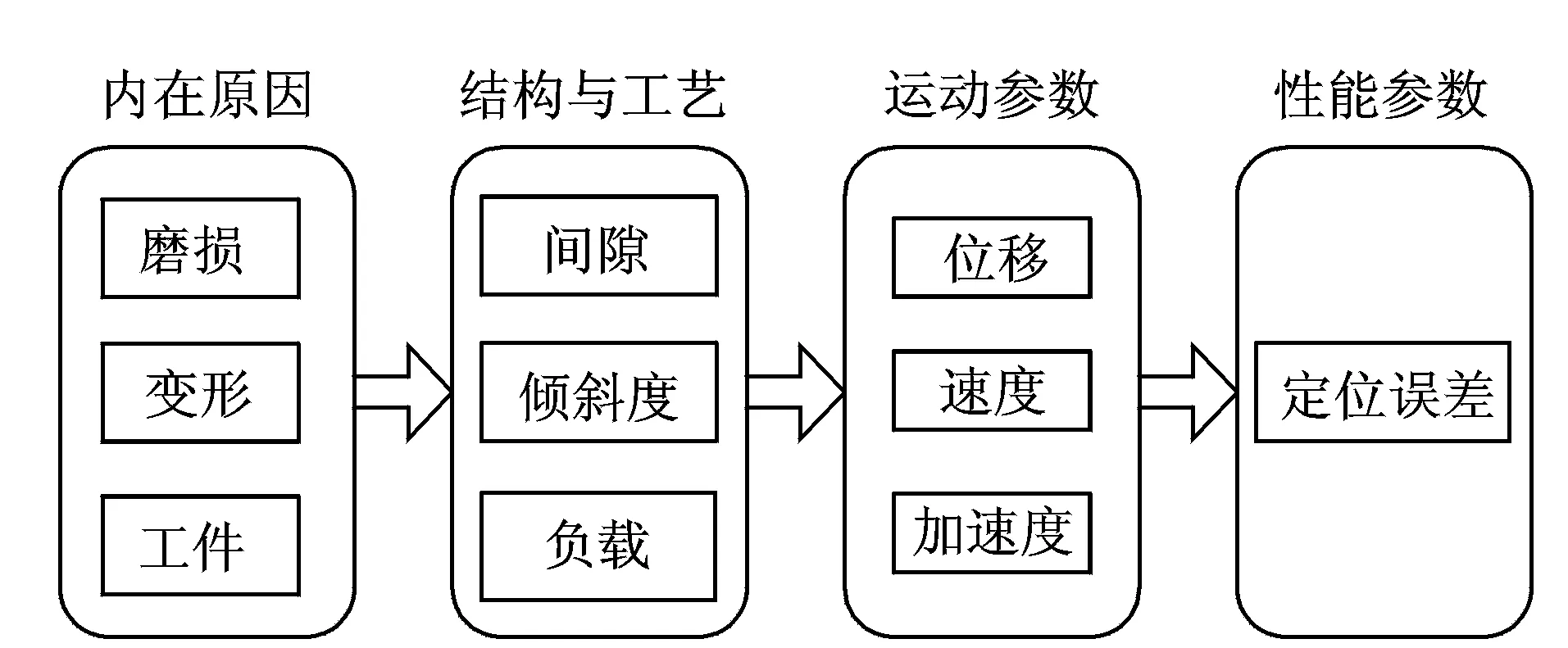
圖1 機械傳動系統(tǒng)部件與定位誤差內(nèi)在關系Fig.1 The intrinsic relationship between component of mechanical transmission system and positioning accuracy

設由于α,β,F而引起的定位誤差為g(α,β,F)，其他因素等引起的定位誤差為A0。在不考慮因腐蝕、熱變形等因素導致的定位誤差A增大的情況下，A的增大主要是由α,β,F的增大引起的。設A0保持不變，則機械傳動系統(tǒng)定位誤差A可以表示為

A=g1(α，β，F(xiàn))=g(α，β，F(xiàn))+A0

(1)

對于大多數(shù)數(shù)控機床而言，在其壽命時間里，極限加工是很少的，大部分都具有較為固定的加工零部件和工藝范圍，中等工況居多?；诖?，在一種工況下假設工件負載F保持不變。進給伺服系統(tǒng)磨損過程包括磨合階段、穩(wěn)定磨損階段和急劇磨損階段。在急劇磨損階段，因磨損而引起的α，β的增大滿足一定規(guī)律。β的增大主要是由于導軌副的磨損而引起的，β與直線度誤差B之間滿足β=arctanB。根據(jù)等價無窮小替換，當B→0時，β～B。進給伺服系統(tǒng)實際工作中，B與β都是在非常小的范圍內(nèi)變化，所以β～B。根據(jù)文獻[2]，導軌副的體積磨損與滑動行程呈正比，導軌直線度B隨時間t的衰減是線性的，所以β隨時間t衰減也為線性關系，設為

β=f(t)=kt+b

(2)

工作臺與螺母座間隙α是進給系統(tǒng)重要的非線性環(huán)節(jié)，α的增大主要是由于傳動部件磨損而引起的[5-6]，α增大會導致反向間隙誤差C增大，α與C之間近似滿足α=C。假設α=h(t)，指數(shù)函數(shù)對設備的退化規(guī)律有良好的表征，因而筆者用指數(shù)函數(shù)表征α的衰減，設為

α=h(t)=a+bexp(ct)

(3)

2 進給伺服系統(tǒng)建模仿真

2.1 進給伺服系統(tǒng)建模

通過Proe(Pro/Engineer)建立數(shù)控機床進給伺服系統(tǒng)三維模型，如圖2所示。各零件的材料、尺寸等屬性均按照所建立的精密運動可靠性試驗平臺實際參數(shù)進行設置。

圖2 進給伺服系統(tǒng)三維模型Fig.2 The 3D model of feed system

將模型導入Adams(automaticdynamicanalysisofmechanicalsystems,簡稱Adams)中，添加運動副、摩擦力和驅(qū)動力矩，具體如下:

1) 對虛擬樣機添加運動副；

2) 對虛擬樣機添加摩擦力以及驅(qū)動力矩，設置導軌處移動副摩擦因數(shù)為0.003，重力加速度為9 800mm/s2，x和y軸添加恒定的驅(qū)動力矩為8和45 Nmm;

3) 設置進給伺服系統(tǒng)x軸的間隙αx和傾斜度βx，y軸的間隙αy和傾斜度βy的初始值，用工作臺垂直方向負載F表示擾動輸入;

4) 添加運動副、驅(qū)動力及負載完成后，驗證模型自由度個數(shù)，確保正確性。

得到進給伺服系統(tǒng)動力學模型如圖 3所示。

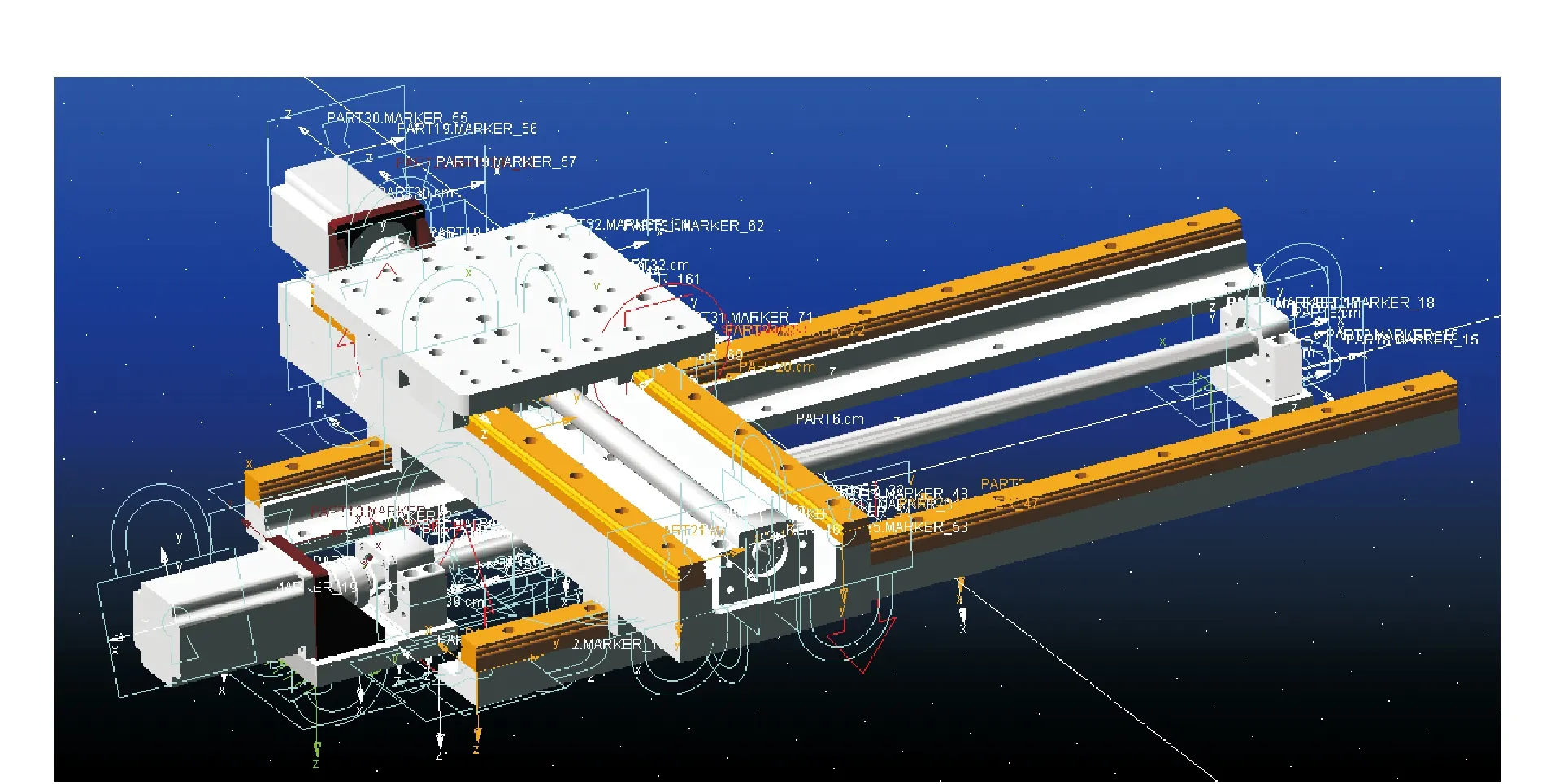
圖3 進給伺服系統(tǒng)Adams仿真模型Fig.3 The Adams simulation model of feed system

2.2 數(shù)值仿真

設αx,αy,βx及βy為不同值， 采用控制變量法分析αx,αy,βx,βy以及F對工作臺輸出的影響。保持恒定的驅(qū)動力距，仿真時間為2s，步距為0.001s。設置α，β及F均為0，然后進行仿真，運動過程如圖 4(a)所示，工作臺位移、速度和加速度輸出如圖 4(b)所示。將αx,αy,βx,βy及F均為0時位移數(shù)據(jù)設為工作臺第0組輸出。改變αx，αy，βx，βy及F，

得到不同初始狀態(tài)下的位移數(shù)據(jù)，然后與第0組輸出相比較，獲得x軸定位誤差Ax及y軸定位誤差Ay。

αx,αy,βx,βy及F取值見圖4，獲得55=3 125組仿真數(shù)據(jù)。

對工作臺位移輸出數(shù)據(jù)進行處理得到Ax和Ay，部分數(shù)據(jù)如表 1所示。

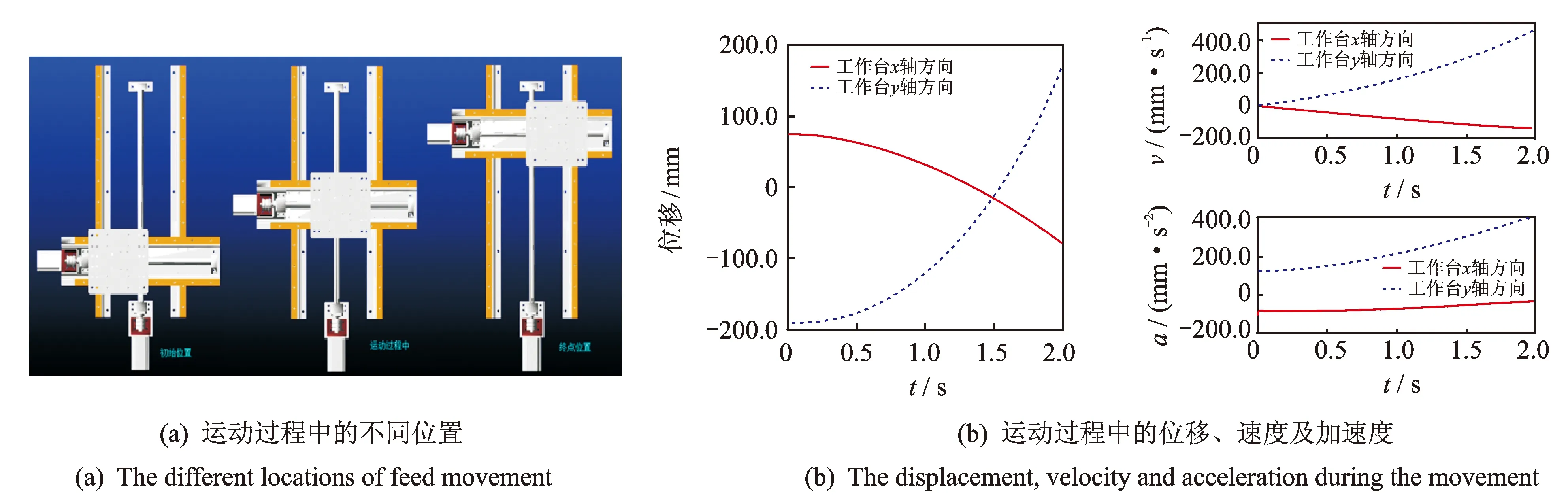
圖4 運動過程的仿真Fig.4 The simulation of the movement

組號初始狀態(tài)Ay/μmAx/μm0F=0N,βx=0°,βy=0°,αx=0mm,αy=0mm001F=0N,βx=0°,βy=0°,αx=0mm,αy=0.001mm0.601.12????3123F=0.004N,βx=0.0004°,βy=0.0004°,αx=0.004mm,αy=0.003mm10.7021.003124F=0.004N,βx=0.0004°,βy=0.0004°,αx=0.004mm,αy=0.004mm11.1121.91

3 基于BP神經(jīng)網(wǎng)絡的映射模型

3.1 BP神經(jīng)網(wǎng)絡模型設計

設置F不變，α和β分別增加時，定位誤差A成單調(diào)遞增的趨勢，但α，β與A之間的經(jīng)驗公式(1)難以確定。一個精煉的BP神經(jīng)網(wǎng)絡不需要任何先驗公式，就能自動歸納已有數(shù)據(jù)的規(guī)則，獲得這些數(shù)據(jù)的內(nèi)在規(guī)律。神經(jīng)網(wǎng)絡被廣泛應用于故障診斷、性能退化及預測[7-8]。 筆者采用BP神經(jīng)網(wǎng)絡建立α，β，F(xiàn)與定位誤差A的映射模型，代替經(jīng)驗公式(1)。

BP網(wǎng)絡的輸入輸出層以及隱層的確定較為關鍵[9]。選擇αx，αy，βx，βy及F作為輸入量，機械傳動系統(tǒng)定位誤差Ax，Ay作為目標輸出。對于隱含層的神經(jīng)元個數(shù)，不能通過理想的公式來獲得，一般根據(jù)經(jīng)驗和多次試驗來確定[10-11]。經(jīng)過多次試驗、調(diào)整，選擇隱含層神經(jīng)元個數(shù)為7個，BP網(wǎng)絡映射模型如圖 5所示。S型函數(shù)可以很好地處理和逼近非線性的輸入/輸出關系，所以選取S型雙曲正切函數(shù)為隱含層神經(jīng)元傳遞函數(shù)，S型對數(shù)函數(shù)為輸出層神經(jīng)元傳遞函數(shù)[12]。

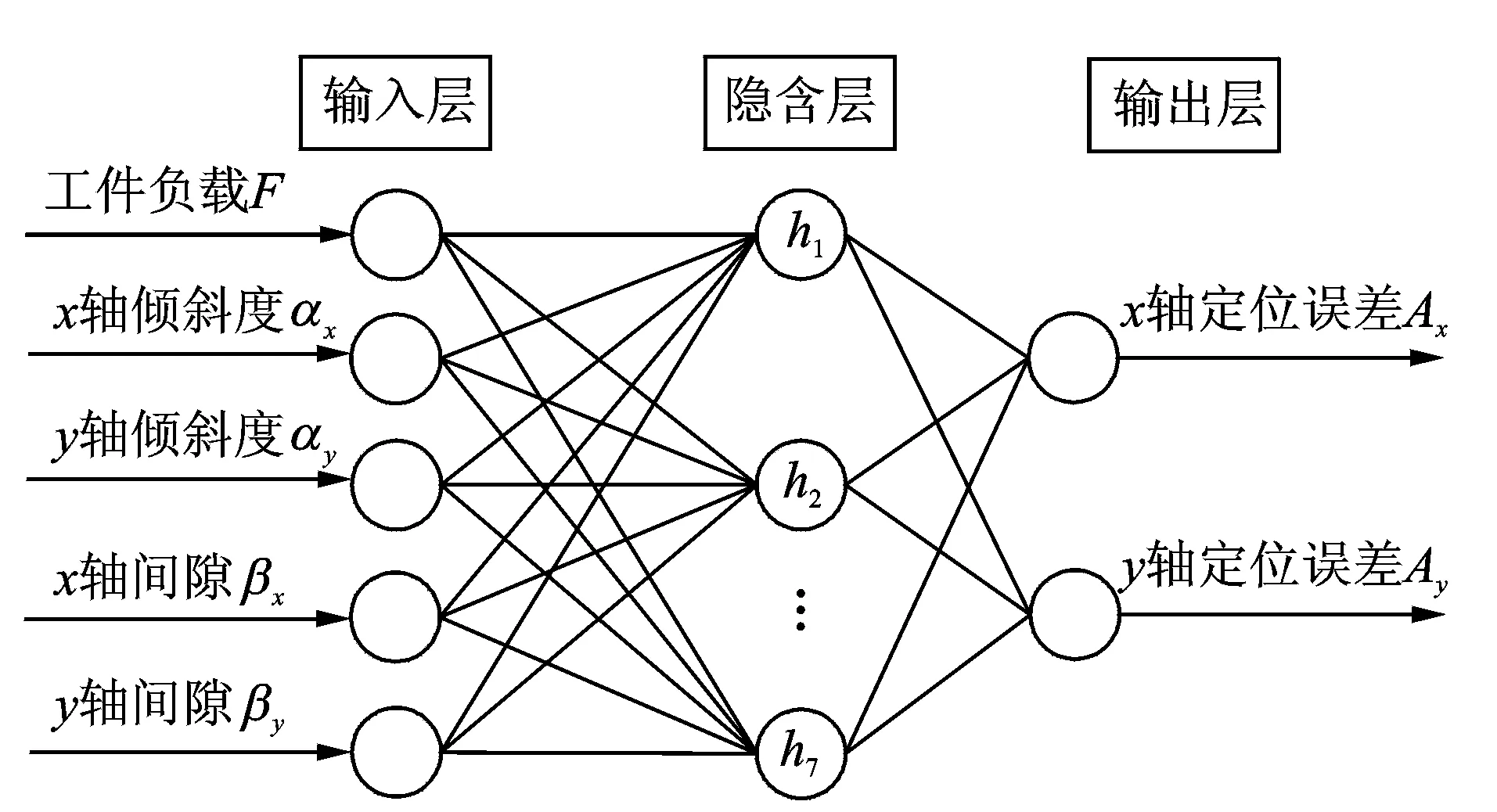
圖5 BP網(wǎng)絡映射模型Fig.5 The BP network mapping model

3.2 網(wǎng)絡訓練及預測

以Adams仿真獲得的前3 100組數(shù)據(jù)作為訓練樣本，后25組數(shù)據(jù)作為預測樣本。在進行網(wǎng)絡訓練之前，利用premnmx函數(shù)對數(shù)據(jù)進行歸一化處理，讓輸入樣本和輸出樣本數(shù)據(jù)都處在[-1,1]或[0,1]之間[13]。樣本數(shù)據(jù)歸一化完成后，通過設計的模型完成對網(wǎng)絡的訓練。設定其學習訓練速率η=0.025，初始權值的收斂因子ξ=1.5×10-4，并對初始權值和閾值進行修正，使所創(chuàng)建網(wǎng)絡的誤差平方和降到最小。

本研究規(guī)定如果訓練計算50 000次仍然沒有收斂時，將對BP神經(jīng)網(wǎng)絡重新調(diào)整其始值的大小，而后再進行訓練。

BP網(wǎng)絡學習曲線如圖 6所示，可以看出網(wǎng)絡訓練得出的誤差小于1μm，達到目標值。在35 647次訓練時達到目標值1.5×10-5。

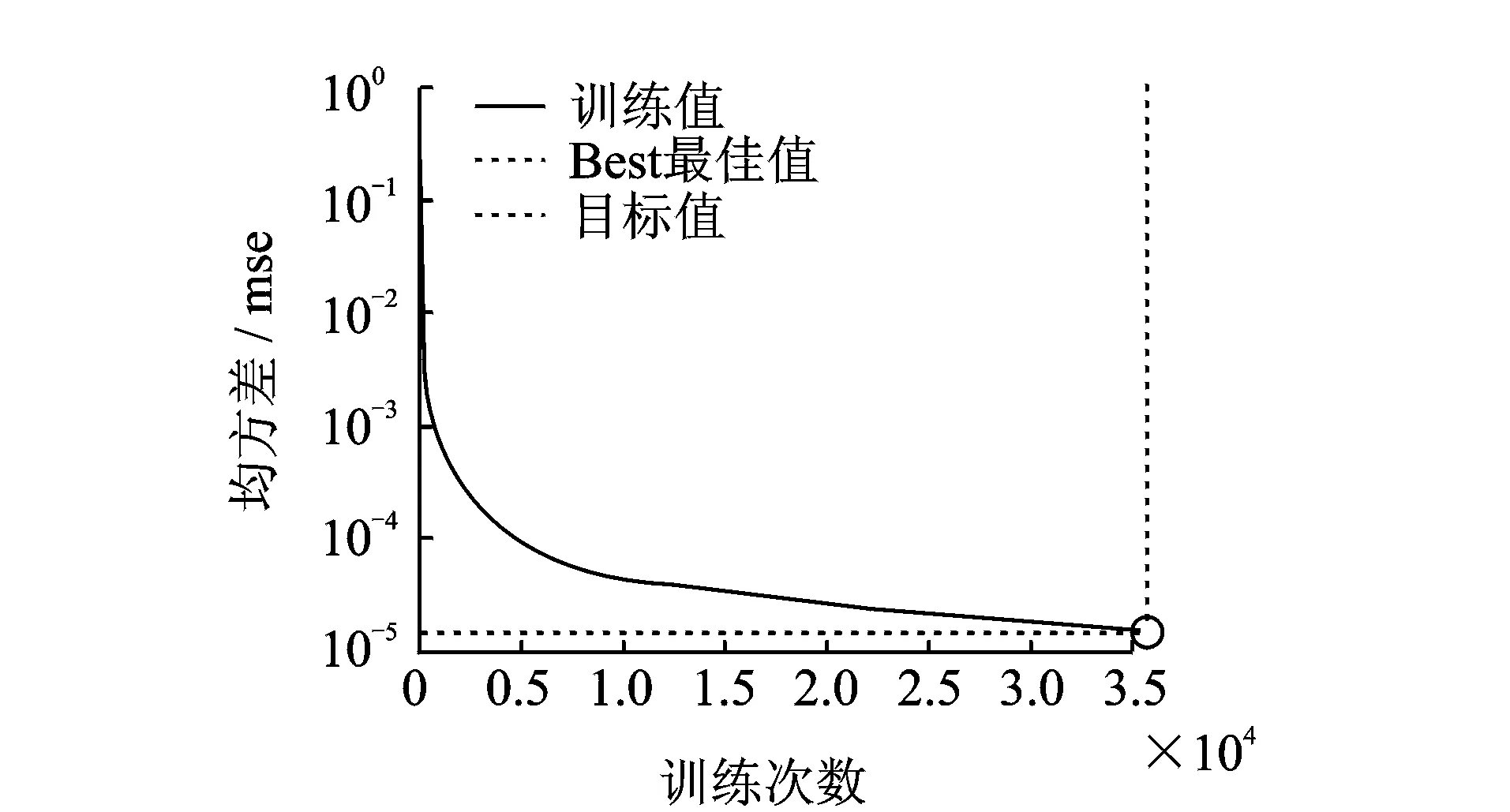
圖6 BP網(wǎng)絡學習曲線Fig.6 The learning curve of BP network

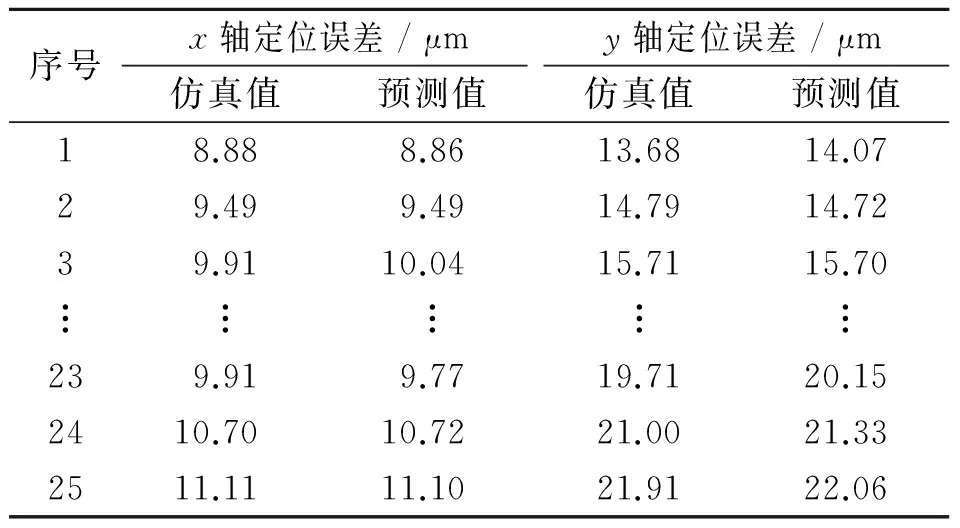
根據(jù)訓練的BP網(wǎng)絡對預測樣本中的仿真數(shù)據(jù)進行預測，得到x軸和y軸定位誤差的預測值。表 2列出了預測樣本的仿真值和預測值。

預測樣本中x軸和y軸定位誤差仿真值和預測值的變化趨勢如圖 7所示。根據(jù)表2能夠計算出平均相對預測誤差為2%，說明BP網(wǎng)絡映射模型是有效的。

表2 定位誤差的仿真值和預測值

Tab.2 The simulation values and predicted values of positioning error

序號x軸定位誤差/μmy軸定位誤差/μm仿真值預測值仿真值預測值18.888.8613.6814.0729.499.4914.7914.7239.9110.0415.7115.70?????239.919.7719.7120.152410.7010.7221.0021.332511.1111.1021.9122.06

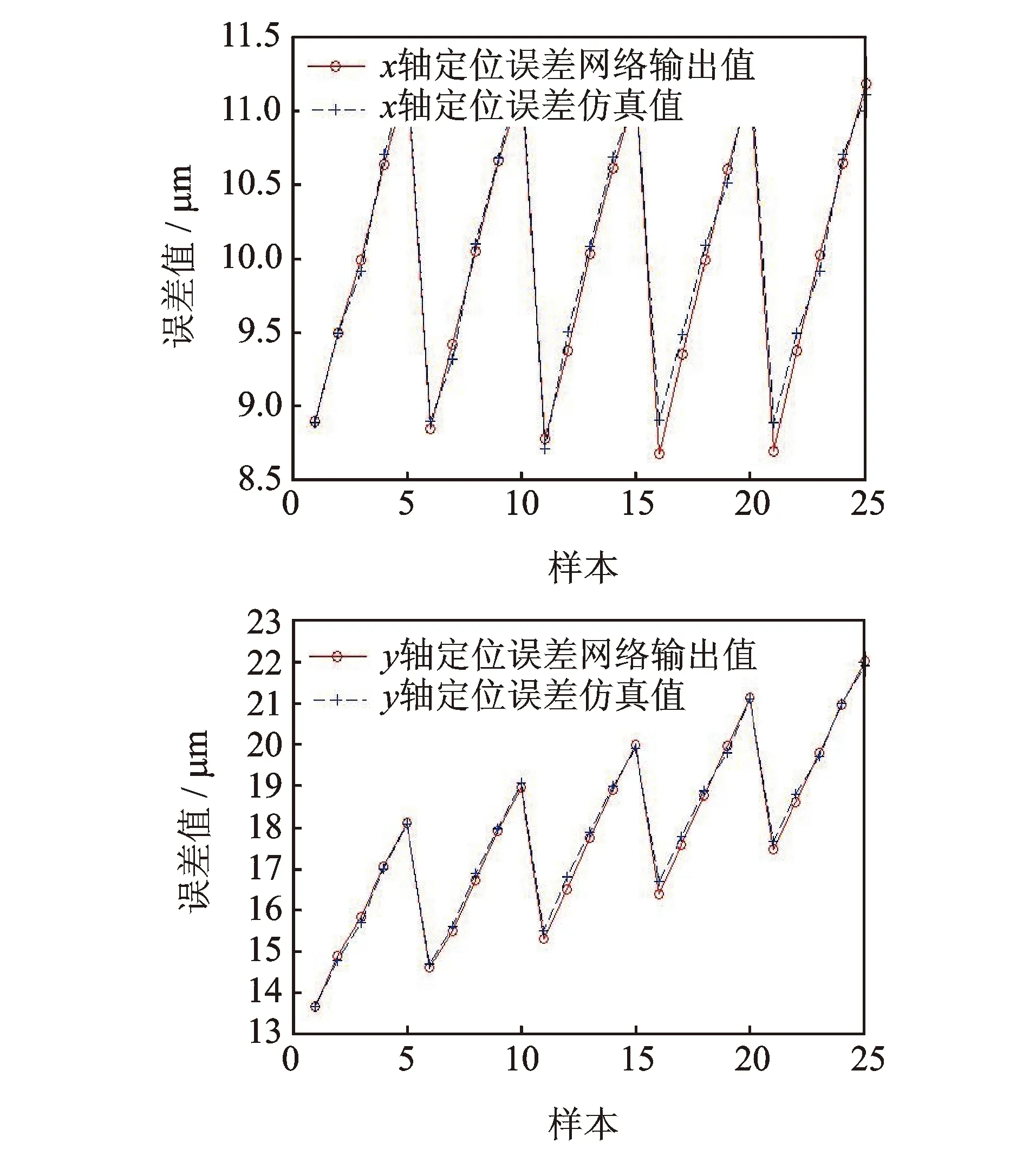
圖7 定位誤差仿真值和預測值變化趨勢Fig.7 The trend of the simulation values and predicted values of positioning error

4 定位誤差的預測

設工件負載F為定值，根據(jù)試驗測得的直線度誤差、反向間隙誤差以及訓練好的BP網(wǎng)絡映射模型能夠?qū)崿F(xiàn)對進給伺服系統(tǒng)機械傳動系統(tǒng)定位誤差的預測，如圖8所示。

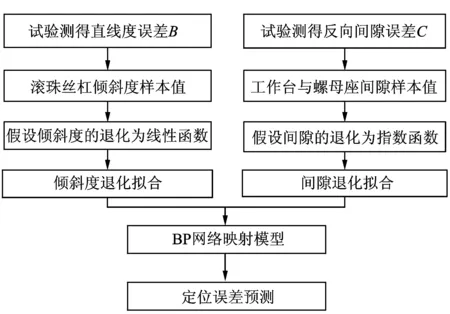
圖8 基于BP網(wǎng)絡的定位誤差預測流程圖Fig.8 The prediction method of positioning accuracy based on BP network

滾珠絲杠傾斜度β的擬合方法、工作臺與螺母座間隙α的擬合方法及定位誤差的預測方法如下。

4.1 滾珠絲杠傾斜度β的擬合

設進給伺服系統(tǒng)x軸滾珠絲杠傾斜度βx和y軸滾珠絲杠傾斜度βy的退化規(guī)律分別為

βx=k1t1+b1

(4)

βy=k2t2+b2

(5)

設試驗測得進給伺服系統(tǒng)工作臺運動的x軸直線度誤差為Bx，y軸直線度誤差為By，由前文分析βx～Bx和βy～By，通過弧度轉(zhuǎn)換角度公式，計算出βx和βy的樣本值。根據(jù)式(4)、式(5)，通過最小二乘法對βx，βy進行擬合。

4.2 工作臺與螺母座間隙α的擬合

設進給伺服系統(tǒng)x軸工作臺與螺母座間隙αx，y軸工作臺與螺母座間隙的退化規(guī)律分別為

αx=a1+b1exp(c1t)

(6)

αy=a2+b2exp(c2t)

(7)

設試驗測得進給伺服系統(tǒng)工作臺運動的x軸反向間隙誤差為Cx，y軸反向間隙誤差為Cy，αx與Cx之間近似滿足αx=Cx，αy與Cy之間近似滿足αy=Cy，能夠得到αx和αy的樣本值。根據(jù)式(6)、式(7)，通過最小二乘法對αx和αy進行擬合。

4.3 基于BP網(wǎng)絡的定位誤差的預測

設定不同的工件負載F，根據(jù)擬合的αx，αy，βx及βy的退化規(guī)律以及BP網(wǎng)絡映射模型對x軸定位誤差Ax及y軸定位誤差Ay進行預測，并計算相應的預測誤差。預測誤差最小時，工件負載F與實際最為接近，這一狀態(tài)下Ax和Ay即為定位誤差的預測值。

5 實例驗證

5.1 試 驗

根據(jù)建立的精密運動可靠性試驗平臺對定位誤差預測方法進行驗證。試驗平臺如圖 9所示，基本設計參數(shù)如表 3所示。試驗平臺具有x,y兩個方向的運動，采用半閉環(huán)伺服運動控制，通過光柵尺測試工作臺實際位置，能動態(tài)實時獲取各軸運動到設定位置時旋轉(zhuǎn)編碼器和光柵尺位置的差值，每隔一段時間獲取并保存一組測量數(shù)據(jù)。

圖9 精密運動可靠性試驗平臺Fig.9 The test platform of precision motion reliability

參數(shù) 參數(shù)值x方向工作行程/mm500y方向工作行程/mm300重復定位精度/μm5數(shù)據(jù)采集最小周期/ms0.5長×寬×高/mm1000×750×1000插補計時器脈沖/ms2

5.2 驗 證

通過數(shù)控編程使工作臺在xOy平面內(nèi)運動，軌跡為450 mm×250 mm的矩形，工作臺每天24 h運行，每天導出1次數(shù)據(jù)，每相隔30 d處理1次數(shù)據(jù)。根據(jù)導出的數(shù)據(jù)計算出試驗臺機械傳動系統(tǒng)定位誤差Ax和Ay、直線度誤差Bx和By、反向間隙誤差Cx和Cy。表 4列出了每相隔30d測得的試驗臺誤差數(shù)據(jù)。

由滾珠絲杠傾斜度β的擬合方法，得到x軸滾珠絲杠傾斜度βx和y軸滾珠絲杠傾斜度βy的退化規(guī)律分別為

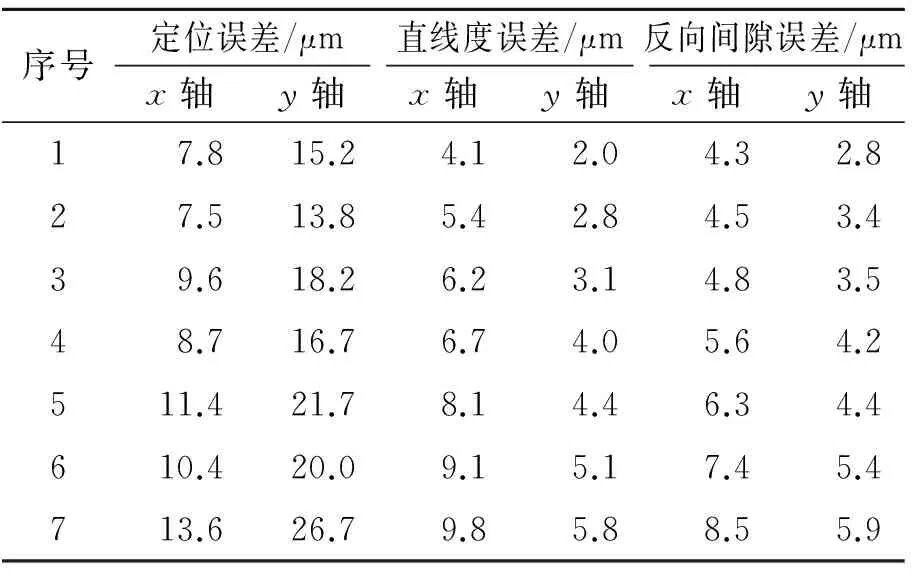
表4 精密運動可靠性試驗平臺試驗數(shù)據(jù)

由工作臺與螺母座間隙α的擬合方法，得到x軸工作臺與螺母座間隙αx及y軸工作臺與螺母座間隙αy的退化規(guī)律分別為

αx=(2.963 1+0.951 7exp(0.251 0t))×10-3

αy=(0.662 5+1.918 0exp(0.144 7t))×10-3

設定工件負載F，根據(jù)擬合的βx，βy，αx，αy以及BP網(wǎng)絡映射模型對x軸、y軸定位誤差Ax，Ay進行預測。經(jīng)過反復驗算，當擾動輸入F=0.001N時，定位誤差預測值和實際值最為接近。表 5列出了x軸和y軸定位誤差的實際值和預測值。

表5 定位誤差的實際值和預測值

Tab.1 The actual values and predicted values of positioning error

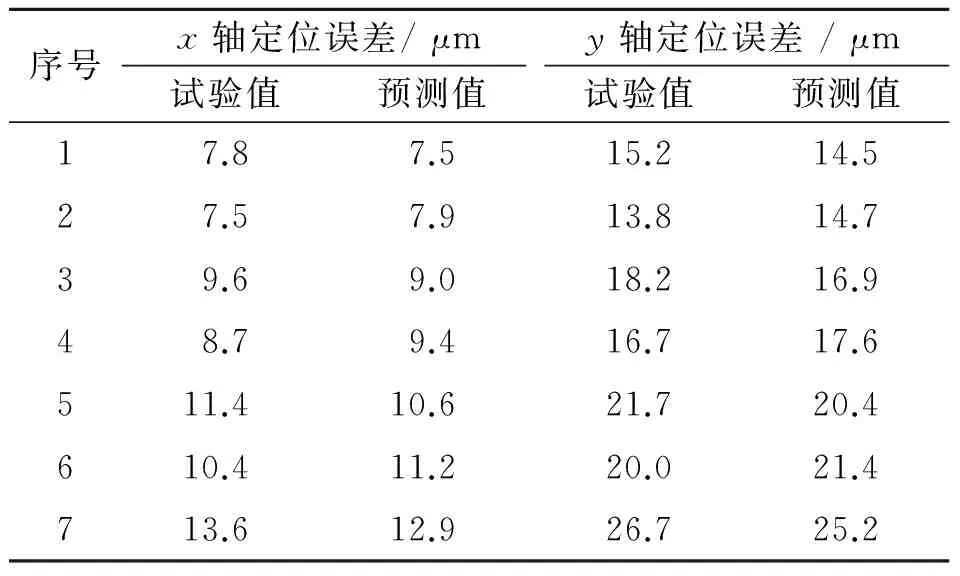
序號x軸定位誤差/μmy軸定位誤差/μm試驗值預測值試驗值預測值17.87.515.214.527.57.913.814.739.69.018.216.948.79.416.717.6511.410.621.720.4610.411.220.021.4713.612.926.725.2

根據(jù)表 5能夠計算出x軸和y軸定位誤差預測值和試驗值的平均相對誤差為6.4%，造成預測誤差的原因有:a.試驗的測量誤差;b.BP網(wǎng)絡本身的訓練誤差;c.計算誤差，即通過BP網(wǎng)絡映射模型采樣以及函數(shù)參數(shù)擬合產(chǎn)生的誤差?？朔斐蛇@3種誤差的因素，可以使預測結果更為精確。與之相比較，對試驗平臺x軸和y軸定位誤差試驗數(shù)據(jù)直接進行指數(shù)函數(shù)擬合，平均相對誤差為8.1%，說明筆者所提出的預測方法具有良好的預測性能。

6 結 論

1) 建立了進給伺服系統(tǒng)工作臺與螺母座間隙、滾珠絲杠傾斜度、工件負載等與定位誤差之間的BP網(wǎng)絡映射模型。在對定位誤差增長機理分析的基礎上，利用所建立的BP網(wǎng)絡映射模型對定位誤差進行預測。以所建立的精密運動可靠性試驗平臺進行實例驗證，預測值與實際值之間的誤差較小，預測精度較高。通過與對定位誤差試驗數(shù)據(jù)直接進行指數(shù)函數(shù)擬合的對比，該方法表現(xiàn)出了良好的預測性能。

2) 在以后的研究中，將建立精密運動可靠性試驗平臺性能參數(shù)體系，進一步分析機床進給系統(tǒng)的多性能退化的內(nèi)在規(guī)律，建立結構工藝變化與多性能之間的映射模型，這對數(shù)控裝備維修決策和壽命預測技術具有重要的意義。

[1] 王勝,劉宏昭.基于神經(jīng)網(wǎng)絡的重型數(shù)控車床定位精度測量與預測[J].機械科學與技術,2011,31(4):604-608.

Wang Sheng , Liu Hongzhao. Laser measurement and prediction of position accuracy for CNC heacy-duty lathe based on netural network[J]. Mechanical and Technology for Aerospace Engineering,2011,31(4):604-608.(in Chinese)

[2] 譚雁清,張連洪,王凱峰,等.基于表面磨損的機床導軌副精度保持性模型[J].農(nóng)業(yè)機械學報,2015,46(2):351-356.

Tan Yanqing , Zhang Lianhong , Wang Kaifeng,et al. Modeling of precision retaining ability for slide guide of machine tool based on wear analysis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(2):351-356.(in Chinese)

[3] 張立新,黃玉美,喬雁龍.混聯(lián)機床并聯(lián)軸定位精度的激光測量與誤差補償[J].農(nóng)業(yè)機械學報,2008,39(2):163-166.

Zhang Lixin , Huang Yumei , Qiao Yanlong . Laser measurement and errors compensation of position accuracy for parallel axis on hybrid NC machine tools[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008,39(2):163-166.(in Chinese)

[4] Wang Yuanhang, Deng Chao, Wu Jun, et al. Failure time prediction for mechanical device based on the degradation sequence[J]. Journal of Intelligent Manufacturing, 2013,12(5):1-19.

[5] 李斌,李曦.數(shù)控技術[M].武漢:華中科技大學出版社, 2010: 224-225.

[6] 李正守, 郭立新, 樸慧日,等. 活塞氣缸拍擊特性及其磨損間隙變化關系[J]. 振動、測試與診斷, 2014,34(5):838-843.

Li Zhengshou, Guo Lixin, Piao Huiri , et al. Piston slap characteristics and clearance variation of piston and cylinder[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(5):838-843.(in Chinese)

[7] 陳樹越,余紅英,劉廣璞.BP網(wǎng)絡算法及其在故障診斷中的應用述評[J].振動、測試與診斷,2001,21(2):100-107.

Chen Shuyue , Yu Hongying , Liu Guangpu. A review of back-propagation algorithm and its application to fault diagnosis[J].Journal of Vibration, Measurement & Diagnosis , 2001,21(2):100-107.(in Chinese)

[8] 時建峰,程珩,許征程,等. 小波包與改進BP神經(jīng)網(wǎng)絡相結合的齒輪箱故障識別[J]. 振動、測試與診斷,2009,29(3):321-324.

Shi Jianfeng, Cheng Hang, Xu Zhengcheng, et al. Fault diagnosis of gearbox using wavelet package and improved BP neural network[J].Journal of Vibration, Measurement & Diagnosis, 2009,29(3):321-324.(in Chinese)

[9] 孫春華,朱荻,李志永.基于BP神經(jīng)網(wǎng)絡的電解加工精度預測模型[J].華南理工大學學報:自然科學版,2004,32(10):24-27.

Sun Chunhua , Zhu Di , Li Zhiyong . Prediction of the workpiece accuracy during the electrochemical machini-ng based on BP neural network[J]. Journal of South China University of Technology:Natural Science Edition, 2004,32(10):24-27.(in Chinese)

[10]Dong Jingwei, Sun Meiting, Liang Gengrui, et al. The improved neural network algorithm of license plate recognition[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2015,8(5):49-54.

[11]Ding Shifei, Su Chunyang, Yu Junzhao. An optimizing BP neural net-work algorithm based on genetic algorithm[J]. Artificial Intelligence Review, 2011, 36(2): 153-162.

[12]Cooper G R. Spinning projectile with an inviscid liquid payload impregnating porous media[J]. Amer Inst Aeronaut Astronaut Journal, 2008,46(3):783-787.

[13]韓慶楠,郝燕玲,劉志平,等.基于BP神經(jīng)網(wǎng)絡的GFSINS角速度預測[J].華中科技大學學報:自然科學版,2011,39(3):115-119.

Han Qingnan , Hao Yanling , Liu Zhiping, et al . Prediction of the angular velocity of GESINS by BP netural network[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2011,39(3):115-119.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.005

國家自然科學基金資助項目(51375181,51475189);國家重點研發(fā)計劃政府間專項資助項目(2016YFE0121700)

2015-05-19；

2015-07-13

TH17； TP306

鄧超，女，1970年5月生，教授、博士生導師。主要研究方向為質(zhì)量管理與可靠性工程。曾發(fā)表《基于隱Markov模型的重型數(shù)控機床健康狀態(tài)評估》 (《計算機集成制造系統(tǒng)-CIMS》 2013年第119卷第3期)等論文。

E-mail: dengchao@hust.edu.cn