基于KPCA和WPHM的滾動(dòng)軸承可靠性評(píng)估與壽命預(yù)測(cè)
王奉濤, 陳旭濤, 柳晨曦, 李宏坤, 韓清凱, 朱 泓
(大連理工大學(xué)機(jī)械工程學(xué)院 大連, 116024)
?
基于KPCA和WPHM的滾動(dòng)軸承可靠性評(píng)估與壽命預(yù)測(cè)
王奉濤, 陳旭濤, 柳晨曦, 李宏坤, 韓清凱, 朱 泓
(大連理工大學(xué)機(jī)械工程學(xué)院 大連, 116024)
為了評(píng)估滾動(dòng)軸承的可靠性和預(yù)測(cè)剩余使用壽命,選取能夠反映性能退化過程的特征參數(shù)作為壽命預(yù)測(cè)模型的輸入?yún)?shù),提出一種基于核主元分析(kernel principal component analysis,簡(jiǎn)稱KPCA)和威布爾比例故障率模型(Weibull proportional hazards model, 簡(jiǎn)稱WPHM)的方法。首先,提取滾動(dòng)軸承全壽命周期的時(shí)域、頻域及時(shí)頻域等多特征參數(shù),從中篩選出有效的特征參數(shù),構(gòu)建高維相對(duì)特征集;其次,進(jìn)行核主元分析,選取能夠反映軸承全壽命周期性能退化過程的核主元,進(jìn)而作為WPHM的協(xié)變量來進(jìn)行可靠性評(píng)估和剩余壽命預(yù)測(cè)。通過滾動(dòng)軸承全壽命試驗(yàn),驗(yàn)證了該方法能夠?qū)S承進(jìn)行準(zhǔn)確的可靠性評(píng)估和剩余壽命預(yù)測(cè),以提供及時(shí)的維修決策。同時(shí),由于提取的是相對(duì)特征,降低了同種軸承間在制造、安裝及工況的差異,增強(qiáng)了該方法的適用性和穩(wěn)定性。
滾動(dòng)軸承;壽命預(yù)測(cè);核主元分析;威布爾比例故障率模型;相對(duì)特征
引 言
滾動(dòng)軸承是旋轉(zhuǎn)機(jī)械的關(guān)鍵組成部件之一,其性能的好壞直接影響整臺(tái)機(jī)器能否正常運(yùn)轉(zhuǎn)。在滾動(dòng)軸承發(fā)生損毀之前,對(duì)軸承進(jìn)行主動(dòng)維修保養(yǎng)可以有效避免惡性事故的發(fā)生,最大程度地減少生命財(cái)產(chǎn)損失[1]。有效的維修策略不僅可以減少停機(jī)次數(shù)和降低維修成本,而且可以保障整個(gè)設(shè)備的正常運(yùn)行[2-3]。若要根據(jù)設(shè)備的實(shí)時(shí)狀態(tài)做出正確的維修決策,準(zhǔn)確壽命預(yù)測(cè)所提供的依據(jù)不可或缺。
對(duì)設(shè)備進(jìn)行準(zhǔn)確的壽命預(yù)測(cè)主要面臨兩個(gè)關(guān)鍵問題:a.建立合適的壽命預(yù)測(cè)模型;b.選取能夠準(zhǔn)確反映性能退化過程的特征參數(shù)作為模型輸入?yún)?shù)。隨著信息新技術(shù)的發(fā)展,基于狀態(tài)監(jiān)測(cè)的軸承壽命預(yù)測(cè)方法成為國內(nèi)外研究的熱點(diǎn)[4]。其中比例故障率模型(proportional hazards model, 簡(jiǎn)稱PHM)[5]是一種適用性很強(qiáng)的壽命數(shù)據(jù)統(tǒng)計(jì)分析方法。它對(duì)數(shù)據(jù)分布、殘差分布均無特殊要求,且可以對(duì)截尾數(shù)據(jù)進(jìn)行分析,屬于一種根據(jù)設(shè)備狀態(tài)監(jiān)測(cè)和歷史壽命等數(shù)據(jù)信息建立失效模型的建模方法,在設(shè)備壽命預(yù)測(cè)領(lǐng)域有強(qiáng)大的發(fā)展。丁峰等[6]將基于設(shè)備振動(dòng)信號(hào)的均方根值(root mean square, 簡(jiǎn)稱RMS)和峭度作為協(xié)變量,利用布爾比例故障模型(Weibull proportional hazards,簡(jiǎn)稱WPHM)實(shí)現(xiàn)了對(duì)鐵路機(jī)車輪滾動(dòng)軸承的可靠性評(píng)估。Zhang等[7]基于依賴分析和比例故障率模型,對(duì)固體潤(rùn)滑軸承建立有效的加速壽命試驗(yàn)?zāi)P汀hang等[8]通過混合威布爾比例故障率模型,來預(yù)測(cè)含有多個(gè)失效形式的機(jī)械系統(tǒng)的剩余使用壽命(remaining useful life, 簡(jiǎn)稱RUL)。
以往的研究大多是針對(duì)運(yùn)行狀態(tài)信息直接進(jìn)行時(shí)域統(tǒng)計(jì)分析,然后從中選擇一個(gè)或多個(gè)時(shí)域特征建模。然而單個(gè)特征或單域特征存在評(píng)估能力不足的問題,無法準(zhǔn)確表征軸承性能退化全周期過程,嚴(yán)重影響可靠性評(píng)估和壽命預(yù)測(cè)的準(zhǔn)確性。而時(shí)域、頻域、時(shí)頻域等多域特征雖然能夠綜合地表征全周期軸承的性能退化過程,但特征過多時(shí)存在冗余性,而WPHM的協(xié)變量越多,模型的參數(shù)估計(jì)越困難,因此直接代入多域特征作為WPHM協(xié)變量進(jìn)行壽命預(yù)測(cè)不太現(xiàn)實(shí)。因此,有效剔除對(duì)反映故障特性貢獻(xiàn)不大、甚至不敏感的特征,并降低特征間的相關(guān)性,減少信息冗余,選取準(zhǔn)確表征軸承性能退化過程的特征作為協(xié)變量對(duì)軸承壽命預(yù)測(cè)至關(guān)重要。
主元分析(principal component analysis, 簡(jiǎn)稱PCA),作為一種線性降維方法,廣泛應(yīng)用于提取特征集的主要信息,但復(fù)雜工況下故障機(jī)械的振動(dòng)信號(hào)是非平穩(wěn)和非線性的[9]。Scholkopf等[10]提出的KPCA作為一種非線性分析方法,通過非線性映射將原始數(shù)據(jù)投影到一個(gè)特征空間,然后進(jìn)行主元分析,從而得到具有更好可分性的非線性主元[11],該方法目前已在過程監(jiān)控和故障診斷中得到越來越多的關(guān)注和成功的應(yīng)用。李巍華等[12]提出基于核函數(shù)主元分析的齒輪故障診斷方法,將非線性主元作為特征子空間對(duì)齒輪工作狀態(tài)進(jìn)行分類識(shí)別。Lee等[13]基于KPCA提出了一種新的非線性過程監(jiān)測(cè)技術(shù)。He等[14]從測(cè)量信號(hào)的統(tǒng)計(jì)特征中提取低維主元來表征和監(jiān)測(cè)齒輪箱的狀態(tài)。
針對(duì)WPHM在選取協(xié)變量方面的不足,筆者選取降維后能充分表征軸承性能退化全周期過程的前3個(gè)核主元作為WPHM的協(xié)變量,來進(jìn)行可靠性評(píng)估和剩余壽命預(yù)測(cè)。通過滾動(dòng)軸承全壽命試驗(yàn),驗(yàn)證了該方法能夠?qū)L動(dòng)軸承進(jìn)行準(zhǔn)確的可靠度評(píng)估和剩余壽命預(yù)測(cè),為設(shè)備主動(dòng)維修提供重要的依據(jù)。由于提取的是相對(duì)特征,降低了同種軸承間在制造、安裝及工況的差異,增強(qiáng)了該方法的適用性和穩(wěn)定性。
1 理論基礎(chǔ)
1.1 核主元分析
KPCA的基本思想是利用映射函數(shù)將原始數(shù)據(jù)空間投影到特征空間,再進(jìn)行線性運(yùn)算。具體算法如下。

(1)
2) 矩陣ST對(duì)應(yīng)的特征方程為
λV=STV
(2)
其中:λ為特征值;V為特征向量。
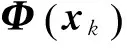
(3)

(4)
其中:aj為相關(guān)系數(shù)。
將式(4)代入式(3)得
(5)
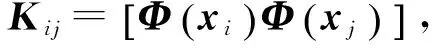
由特征向量a求出ST的特征向量V,得到映射空間F的主元方向。對(duì)K對(duì)角化,λ1≥λ2≥…≥λp≥…≥λN表示K的特征值,a1,a2,…,ap,…,aN為對(duì)應(yīng)的特征向量。設(shè)λp為大于零的最小特征值,對(duì)特征向量進(jìn)行歸一化,令
(6)
5) 計(jì)算m個(gè)測(cè)試樣本在特征空間中前p個(gè)軸的投影為
(7)
其中
對(duì)映射數(shù)據(jù)進(jìn)行中心化,相應(yīng)K變?yōu)?/p>
(8)
其中:lN為系數(shù)為1/N的N×N階單位矩陣。
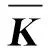
定義累計(jì)貢獻(xiàn)
(9)
其中:p為輸入向量空間維數(shù);ηp為前p個(gè)核主元的累計(jì)貢獻(xiàn)率。
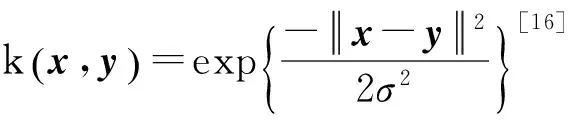
1.2WPHM模型
PHM建立了設(shè)備運(yùn)行狀態(tài)特征與可靠度之間的數(shù)學(xué)關(guān)系,根據(jù)當(dāng)前實(shí)時(shí)運(yùn)行狀態(tài)特征,得到當(dāng)前狀態(tài)的故障率。采用基底函數(shù)為威布爾分布的PHM為WPHM,其故障率函數(shù)為
(10)
其中:β>0為威布爾分布形狀參數(shù);η>0為威布爾分布尺度參數(shù)。
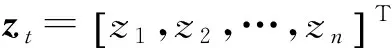
可靠性函數(shù)和概率密度函數(shù)分別為
(11)
(12)
極大似然估計(jì)廣泛用于估計(jì)WPHM的未知參數(shù)。 在實(shí)際中,一個(gè)機(jī)械設(shè)備有時(shí)會(huì)運(yùn)轉(zhuǎn)直至失效,有時(shí)會(huì)在失效前進(jìn)行維修,因此數(shù)據(jù)常常包括失效時(shí)間和刪失時(shí)間。為同時(shí)處理這兩類數(shù)據(jù),似然函數(shù)定義為
(13)
其中:n為失效樣本個(gè)數(shù);m為刪失樣本個(gè)數(shù)。
將式(11)和式 (12) 代到式(13)中,其對(duì)數(shù)似然函數(shù)可化簡(jiǎn)為
(14)
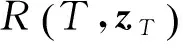
(15)
其中:R0為失效閾值。
剩余壽命誤差定義為
(16)
其中:Tp為預(yù)測(cè)的剩余壽命;Ta為實(shí)際剩余壽命。
2 方法步驟
本方法的具體流程如圖1所示。
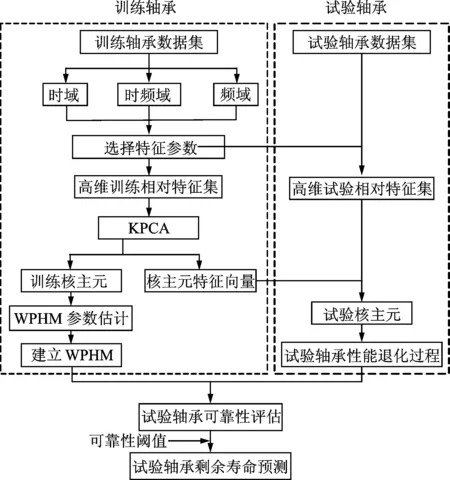
圖1 方法流程圖Fig.1 Flowchart of the proposed method
具體步驟如下。
1) 選擇特征參數(shù):從訓(xùn)練軸承壽命周期數(shù)據(jù)中提取全壽命周期的時(shí)域特征、頻域特征和時(shí)頻域特征參數(shù),從中篩選出能反映軸承性能退化過程的特征參數(shù),構(gòu)成特征向量。
2) 構(gòu)建高維訓(xùn)練相對(duì)特征集:提取訓(xùn)練軸承的壽命周期樣本點(diǎn),構(gòu)建相對(duì)高維訓(xùn)練特征集。
3) KPCA降維:對(duì)高維訓(xùn)練相對(duì)特征集進(jìn)行KPCA降維,選取累計(jì)貢獻(xiàn)率大于85%的核主元和對(duì)應(yīng)的特征向量。
4) 驗(yàn)證軸承性能退化趨勢(shì):構(gòu)建高維試驗(yàn)相對(duì)特征集,通過特征向量映射,得到試驗(yàn)軸承的核主元,驗(yàn)證其能否能夠充分表征軸承性能退化過程,若滿足,即可將核主元作為WPHM的協(xié)變量。
5) 估計(jì)模型參數(shù):將訓(xùn)練軸承的核主元作為WPHM的協(xié)變量來估計(jì)模型的未知參數(shù)。
6) 評(píng)估可靠性和預(yù)測(cè)剩余壽命:將試驗(yàn)軸承的核主元作為WPHM的協(xié)變量來進(jìn)行可靠性評(píng)估和剩余壽命預(yù)測(cè)。
3 協(xié)變量選取方法
3.1 滾動(dòng)軸承試驗(yàn)臺(tái)介紹
本研究中滾動(dòng)軸承全壽命周期試驗(yàn)數(shù)據(jù)由美國辛辛那提大學(xué)智能系統(tǒng)維護(hù)中心(IMS)中心提供[19]。全壽命周期試驗(yàn)臺(tái)裝置如圖2所示。
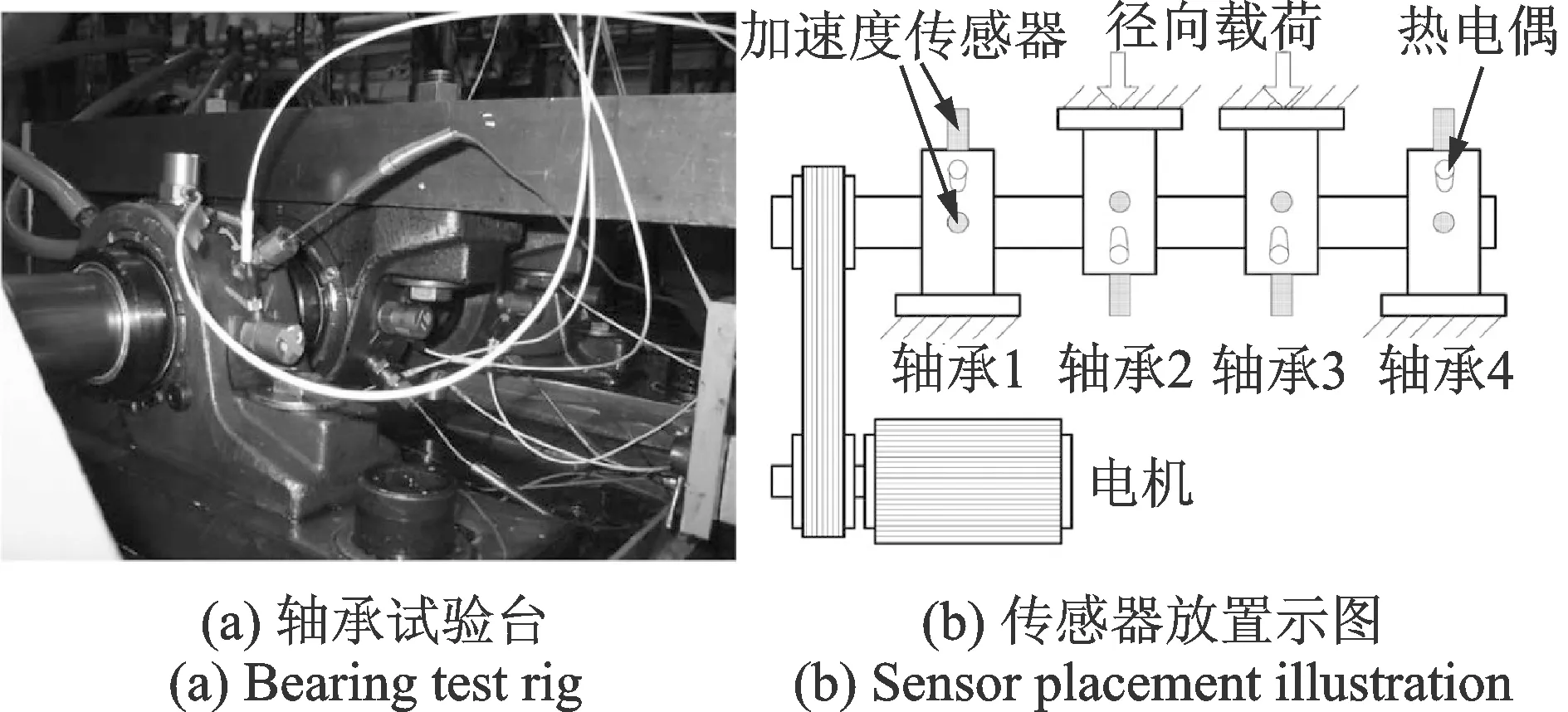
圖2 試驗(yàn)臺(tái)和裝置示意圖Fig.2 Bearing test rig and sensor placement illustration
在同一軸上安裝有4個(gè)Rexnord ZA-2115滾動(dòng)軸承,由直流電機(jī)通過皮帶聯(lián)接驅(qū)動(dòng),軸轉(zhuǎn)速始終保持在2kr/min,軸和軸承共同承受來自彈簧機(jī)構(gòu)施加的26.67kN徑向荷載。在油反饋管道安裝有磁性螺塞,收集潤(rùn)滑油的碎屑用以驗(yàn)證軸承的性能退化。系統(tǒng)電器開關(guān)關(guān)閉由磁性螺塞所吸附的金屬碎屑量決定,隨著軸承性能不斷退化,當(dāng)吸附的碎屑量達(dá)到預(yù)先設(shè)定的閾值,數(shù)據(jù)采集工作便停止。每個(gè)軸承的水平方向和豎直方向各裝一個(gè)PCB 353B33加速度傳感器。振動(dòng)信號(hào)通過美國國家儀器(NI)公司的DAQCardTM-5052E數(shù)據(jù)采集卡每20 min采集一次,采樣率為20kHz,采樣點(diǎn)數(shù)為20 480個(gè)點(diǎn)。試驗(yàn)結(jié)果如表1所示。

表1 試驗(yàn)結(jié)果
a為內(nèi)環(huán)故障;b為滾動(dòng)體故障;c為外環(huán)故障
以3號(hào)軸承(試驗(yàn)1)數(shù)據(jù)作為試驗(yàn)軸承,其他7個(gè)軸承(試驗(yàn)1和試驗(yàn)2)數(shù)據(jù)作為訓(xùn)練軸承。
3.2 滾動(dòng)軸承性能退化高維特征集構(gòu)建
針對(duì)7個(gè)訓(xùn)練軸承的壽命周期數(shù)據(jù),提取各自的時(shí)域、頻域及時(shí)頻域等70多個(gè)特征參數(shù)[20-21]。如果直接對(duì)這70多個(gè)特征參數(shù)進(jìn)行核主元分析,由于包含大量冗余信息及無用信息,降維后前3個(gè)核主元的累計(jì)貢獻(xiàn)率很低,包含的有用信息較少。為使前幾個(gè)核主元包含盡可能多的信息,須在進(jìn)行核主元降維前,保證各維度信息有效性的條件下盡量減少維度。首先,對(duì)每個(gè)特征繪制隨時(shí)間變化的全壽命特征圖,剔除不能反映退化過程的特征,例如均值、偏斜度等;然后,針對(duì)功能或意義相似的特征,通過對(duì)比剔除反映性能退化過程效果相對(duì)差的特征,例如小波包歸一化能量譜與經(jīng)驗(yàn)?zāi)B(tài)分解(empirical mode decomposition, 簡(jiǎn)稱EMD)歸一化能量譜對(duì)比,剔除EMD歸一化能量譜等。得到如下11個(gè)最能反映軸承性能退化過程的特征參數(shù):
1) 時(shí)域包含均方根值、峭度、峰峰值及峰值因子;
2) 頻域包含頻譜均值、頻譜方差及頻譜均方根值;
3) 時(shí)頻域包含3層小波包分解的第3頻帶歸一化小波包能量譜(E3)和第7頻帶歸一化小波包能量譜(E7),以及第3頻帶樣本熵(S3)和第7頻帶樣本熵(S7)。
考慮到各個(gè)軸承制造、安裝和實(shí)際工況的差異,即使是處于同一工作環(huán)境下的同型號(hào)軸承,特征參數(shù)存在一定的差異。以時(shí)域特征參數(shù)為例,對(duì)1~8號(hào)軸承,各自提取正常工作期內(nèi)一段趨勢(shì)平穩(wěn)的時(shí)域特征參數(shù),然后求取平均值,如圖3所示。
圖3 正常期平均時(shí)域特征參數(shù)Fig.3 The mean time domain features in normal work period
由圖3可以明顯看出,8個(gè)軸承平穩(wěn)期的時(shí)域參數(shù)有很大差異。例如圖3(a)中,1號(hào)軸承正常工作期的平均均方根值為0.154,而5號(hào)軸承正常工作期的平均均方根值為0.077。為了降低軸承間特征參數(shù)的影響,需要對(duì)軸承特征參數(shù)進(jìn)行標(biāo)準(zhǔn)化。首先,選取正常期內(nèi)一段趨勢(shì)平穩(wěn)的特征參數(shù),將該段平均值定為標(biāo)準(zhǔn)值;然后,計(jì)算原始特征參數(shù)與標(biāo)準(zhǔn)值之比,得到相對(duì)特征參數(shù)。
對(duì)7個(gè)訓(xùn)練軸承,每個(gè)軸承取100個(gè)樣本點(diǎn)(每個(gè)軸承根據(jù)其全壽命過程,選取能反映壽命過程的100個(gè)點(diǎn)),共計(jì)700個(gè)樣本點(diǎn),構(gòu)成最終的700×11(11為特征參數(shù)個(gè)數(shù))的高維訓(xùn)練相對(duì)特征集。
對(duì)于試驗(yàn)軸承,全壽命周期共有2 152個(gè)采樣點(diǎn),構(gòu)成2 152×11的高維試驗(yàn)相對(duì)特征集,如圖4所示。其中:(a)~(d)為時(shí)域特征;(e)~(g)為頻域特征;(h)~(i)為小波包第3,7頻帶歸一化能量譜;(j)~(k)為小波包第3,7頻帶樣本熵;(l)表示全壽命周期軸承數(shù)據(jù)采集連續(xù)情況,間斷點(diǎn)為空數(shù)據(jù),在此時(shí)間內(nèi)未進(jìn)行數(shù)據(jù)采集。
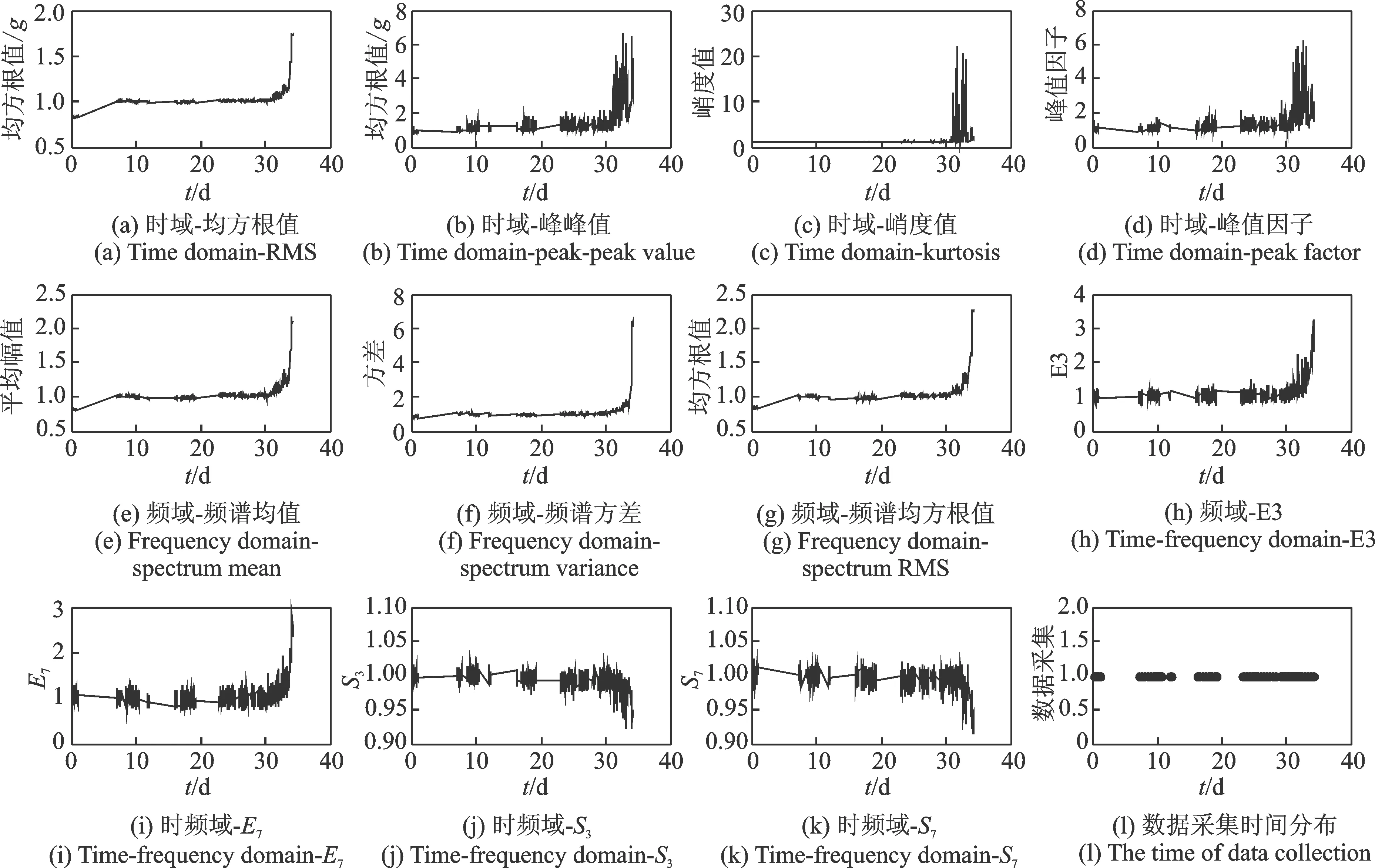
圖4 高維試驗(yàn)相對(duì)特征集Fig.4 High test relative feature set
3.3 滾動(dòng)軸承核主元的性能退化評(píng)估
分別對(duì)特征參數(shù)未相對(duì)化的高維訓(xùn)練絕對(duì)特征集和特征參數(shù)相對(duì)化的高維訓(xùn)練相對(duì)特征集進(jìn)行核主元分析(σ=57),前3個(gè)核主元的特征值和累計(jì)貢獻(xiàn)率如表2所示。

表2 核主元分析結(jié)果對(duì)比
由表2可見,直接對(duì)高維訓(xùn)練絕對(duì)特征集進(jìn)行分析,由于軸承制造、安裝和工況差異引起數(shù)據(jù)離散較大,造成前3個(gè)核主元的累計(jì)貢獻(xiàn)率明顯低于高維訓(xùn)練相對(duì)特征集累計(jì)貢獻(xiàn)率,即前者降維效果低于后者,因此選擇高維訓(xùn)練相對(duì)特征集進(jìn)行核主元分析。
選取前3個(gè)核主元特征值對(duì)應(yīng)的特征向量組成投影空間,對(duì)高維試驗(yàn)相對(duì)特征集進(jìn)行中心化后投影,得到高維試驗(yàn)相對(duì)特征集的核主元。為驗(yàn)證核主元分析效果,將高維試驗(yàn)相對(duì)特征集第1至第3核主元投影到三維空間,第1和第2核主元投影到二維空間,分別如圖5所示,圖中點(diǎn)的位置信息如表3所示。
試驗(yàn)軸承的第1核主元KPC1的貢獻(xiàn)率為63.24%,包含了高維試驗(yàn)相對(duì)特征集的大部分信息,因此在圖5中可以區(qū)分軸承性能退化過程的各個(gè)階段;第2核主元KPC2和第3核主元KPC3的貢獻(xiàn)率分別為17.47%和8.49%,包含了高維試驗(yàn)相對(duì)特征集的少部分信息,因此能區(qū)分軸承性能退化的部分階段。從圖5中可以清晰區(qū)分出正常工作期、早期故障期、磨損中期和急劇后期,其中經(jīng)常忽略的恢復(fù)期也能在圖5中清晰識(shí)別。此外,隨著時(shí)間變化,數(shù)據(jù)點(diǎn)總體上有明顯的趨勢(shì)走向規(guī)律,且變化過程比較平滑。
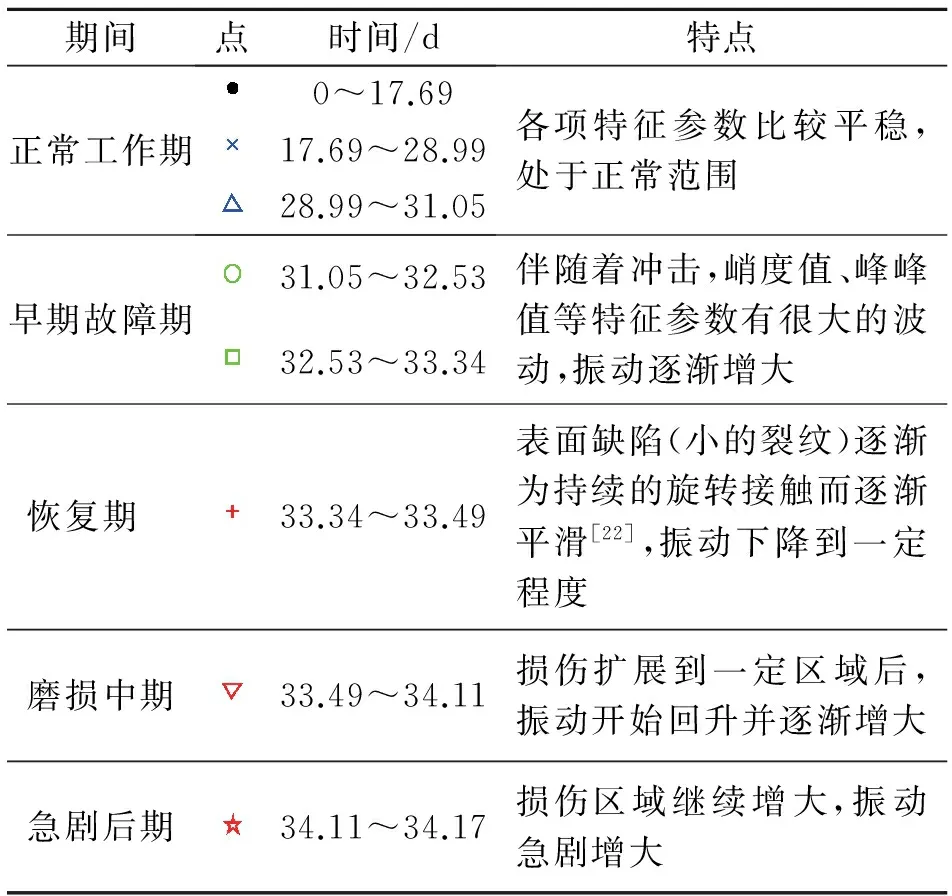
表3 點(diǎn)的位置信息
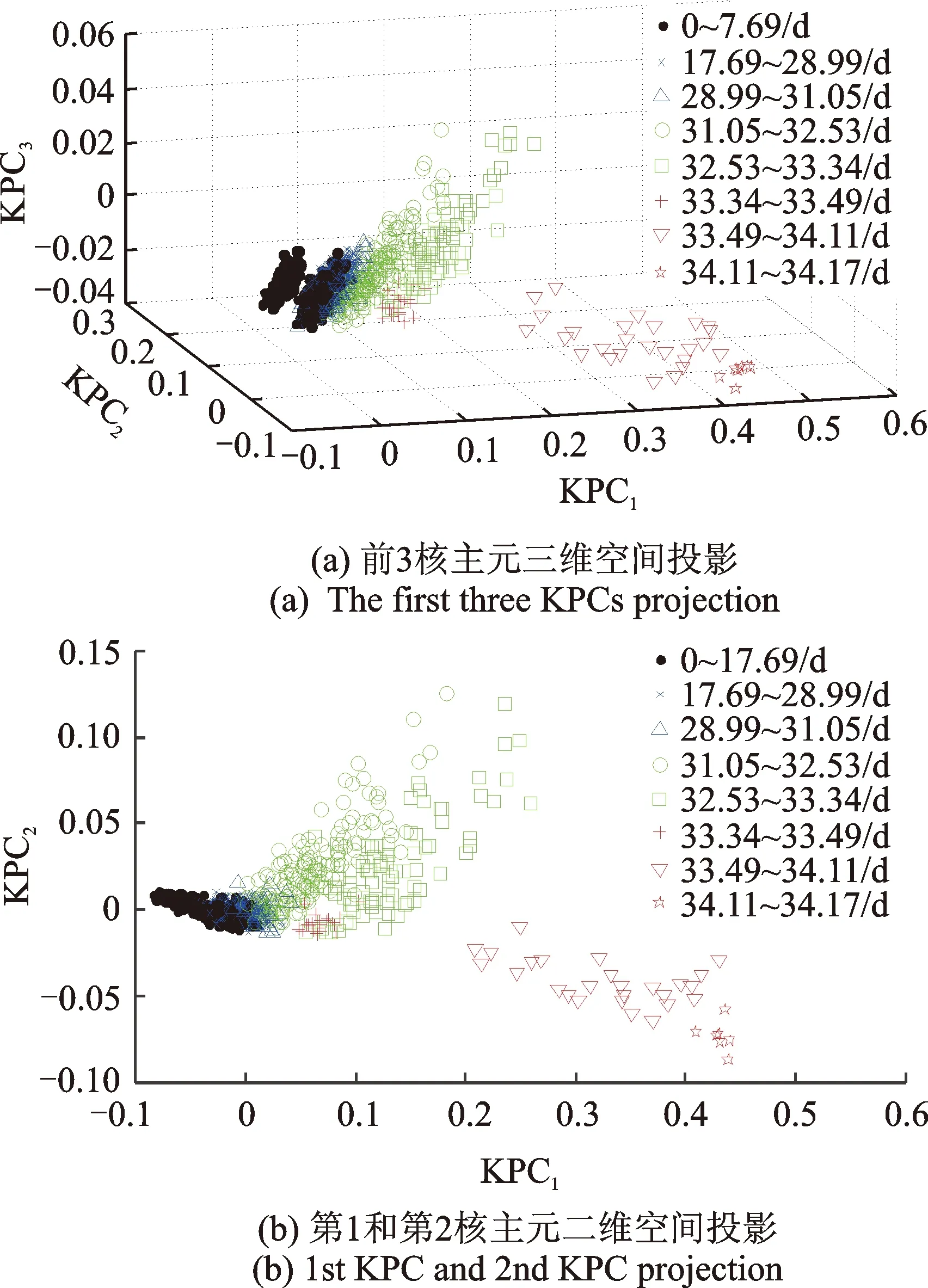
圖5 核主元投影Fig.5 Kernel principal component projection
為與WPHM常規(guī)協(xié)變量進(jìn)行對(duì)比,將試驗(yàn)軸承全壽命周期的均方根值和峭度投影到二維空間,如圖6所示。從圖中可以看出:均方根值雖然能夠區(qū)分正常工作期、早期故障期、磨損中期和急劇后期,但其僅是時(shí)域中的一個(gè)特征參數(shù),從包含的特征信息量上來看,遠(yuǎn)沒有核主元包含的信息多,穩(wěn)定性遠(yuǎn)低于核主元;峭度值僅對(duì)早期故障期區(qū)分比較明顯,無法區(qū)分軸承性能退化過程的其他階段,且早期故障數(shù)據(jù)變化范圍非常大且隨時(shí)間不停振蕩;而在磨損中期和急劇后期只是比正常工作期略微增大,更適合作為早期故障預(yù)警的重要指標(biāo),而不能反映性能退化的過程。
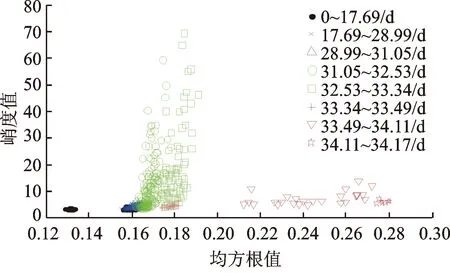
圖6 均方根值、峭度投影Fig.6 RMS and Kurtosis projection
相比前3個(gè)核主元包含了時(shí)域、頻域、時(shí)頻域的絕大部分信息,同時(shí)在變化趨勢(shì)方面,圖5的數(shù)據(jù)點(diǎn)變化比圖6更加平滑,軸承性能退化過程總體趨勢(shì)走向更加明顯。比如在31.05~33.34 d的早期故障期,由于峰峰值、峭度值及峰值因子等變化范圍非常大(圖4),故圖5中早期故障期數(shù)據(jù)點(diǎn)有相對(duì)明顯的偏移,但相對(duì)圖6變化趨勢(shì)更平滑、偏移更小。又如33.49~34.17 d的磨損中期和急劇后期,圖5數(shù)據(jù)點(diǎn)的總體趨勢(shì)走向比圖6更加明顯。整體上來說,隨著時(shí)間的變化,圖5的數(shù)據(jù)點(diǎn)過渡比圖6更加平滑,偏移更小。
綜上,由于前3個(gè)核主元包含時(shí)域、頻域及時(shí)頻域絕大部分信息,且兼顧非線性成分,樣本點(diǎn)間偏離性相對(duì)較小,數(shù)據(jù)點(diǎn)有明顯的趨勢(shì)走向,因此選擇能充分表征軸承性能退化過程的前3個(gè)核主元作為WPHM模型的協(xié)變量來建立模型更加穩(wěn)定可靠。
4 剩余壽命預(yù)測(cè)
4.1 可靠性評(píng)估
將高維訓(xùn)練相對(duì)特征集中核主元的各軸承全壽命數(shù)據(jù)和刪失數(shù)據(jù)帶入式(14)中,求解模型未知參數(shù)的估計(jì)值,如表4所示。

表4 WPHM參數(shù)
將高維試驗(yàn)相對(duì)特征集的核主元帶入式(11)計(jì)算可靠度,如圖7所示。

圖7 全壽命周期可靠度Fig.7 The reliability of lifetime
由圖7可以看出,在正常工作期可靠度的下降速度基本保持不變。早期故障期的下降速度開始增大,磨損中期和急劇磨損期的下降速度急劇增大。由于模型中的協(xié)變量是時(shí)變性的,任一時(shí)刻的可靠度都由歷史數(shù)據(jù)的累積計(jì)算得到,不會(huì)因?yàn)槟硶r(shí)刻采集數(shù)據(jù)突變而突變(如恢復(fù)期),其可信度高于那些僅僅與當(dāng)前時(shí)間有關(guān)計(jì)算得到的可靠度模型。從可靠度下降趨勢(shì)變化就能準(zhǔn)確區(qū)分軸承性能退化的狀態(tài)。
4.2 剩余壽命預(yù)測(cè)
為了驗(yàn)證剩余壽命預(yù)測(cè)方法的準(zhǔn)確度,需設(shè)置可靠度閾值。它一般由統(tǒng)計(jì)學(xué)經(jīng)驗(yàn)設(shè)定。由于式(11)中協(xié)變量是時(shí)變性的,且e-1為特征壽命[23],由圖7可以看出,急劇后期的可靠度值在e-1左右。因此可靠度閾值R0設(shè)置為e-1。當(dāng)然,定義的可靠度閾值并非恒定的,需要依據(jù)歷史數(shù)據(jù)的可靠度和設(shè)備維修經(jīng)驗(yàn)來適當(dāng)?shù)恼{(diào)整。
針對(duì)試驗(yàn)軸承,不同退化時(shí)期共取4個(gè)時(shí)間點(diǎn),預(yù)測(cè)其剩余壽命,結(jié)果如表5所示。依據(jù)式(16)得到對(duì)應(yīng)的誤差率,如圖8所示。可以看出,正常工作期的剩余壽命預(yù)測(cè)值與真實(shí)剩余壽命差別很大,這是因?yàn)檩S承產(chǎn)生損傷是偶發(fā)性的,正常期各項(xiàng)特征處于正常范圍內(nèi),協(xié)變量預(yù)測(cè)趨勢(shì)呈線性,以至于正常期的預(yù)測(cè)誤差較大。隨著步入早期故障,新退化特征的累積,協(xié)變量的預(yù)測(cè)曲線會(huì)越來越準(zhǔn)確,剩余壽命預(yù)測(cè)值也越來越接近真實(shí)的剩余壽命,到磨損中期的33.986 8 d的誤差率為9.84%(即準(zhǔn)確度為1-9.84%= 90.16%)。結(jié)果表明,提出的壽命方法可以準(zhǔn)確地預(yù)測(cè)軸承的剩余壽命,以便及時(shí)提供有效的維修決議。
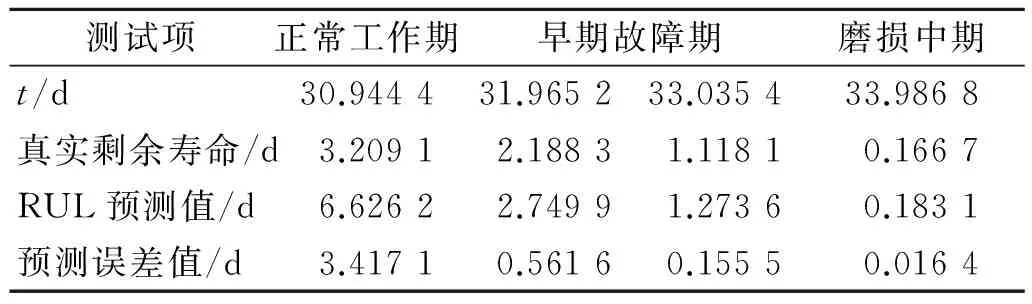
表5 剩余壽命預(yù)測(cè)
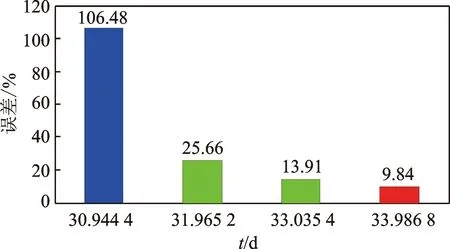
圖8 剩余壽命預(yù)測(cè)誤差度Fig.8 The error percent of RUL prediction
5 結(jié) 論
1) 基于相對(duì)多特征的核主元分析方法,降維后的核主元能夠充分表征軸承性能退化過程。
2) 以包含多域信息的核主元作為WPHM協(xié)變量,能夠準(zhǔn)確預(yù)測(cè)軸承的剩余壽命,及時(shí)提供有效的維修決議,極大地優(yōu)化了WPHM協(xié)變量選取的方法。
3) 相對(duì)特征降低了軸承制造、安裝和實(shí)際工況差異的影響,大大增強(qiáng)了該方法的適用性和穩(wěn)定性。增加新的訓(xùn)練軸承全壽命數(shù)據(jù)不會(huì)引起數(shù)據(jù)離散,且對(duì)新的監(jiān)測(cè)樣本求取相對(duì)特征,映射后帶入模型即可求取可靠度和剩余壽命,為維修計(jì)劃提供有力的支持。
[1] 郭紅.內(nèi)外膜獨(dú)立供油徑推聯(lián)合浮環(huán)軸承性能分析與實(shí)驗(yàn)研究[D].上海:上海交通大學(xué),2009.
[2] Wei Guo, Peter W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals [J]. Journal of Sound and Vibration, 2013,332(2): 423-441.
[3] Cong Feiyun, Chen Jin, Dong Guangming, et al. Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis [J]. Journal of Sound and Vibration, 2013,332 (8): 2081-2097.
[4] 張小麗,陳雪峰,李兵,等. 機(jī)械重大裝備壽命預(yù)測(cè)綜述[J]. 機(jī)械工程學(xué)報(bào), 2011,47(11): 100-116.
Zhang Xiaoli, Chen Xuefeng, Li Bing, et al. Review on life prediction of machinery major equipment [J]. Chinese Journal of Mechanical Engineering, 2011, 47 (11): 100-116. (in Chinese)
[5] Cox D R. Regression models and life-tables (with discussion) [J]. Journal of the Royal Statistical Society, Series B: Methodological, 1972,34(2): 187-220.
[6] 丁鋒,何正嘉,訾艷陽,等. 基于設(shè)備狀態(tài)振動(dòng)特征的比例故障率模型可靠性評(píng)估[J]. 機(jī)械工程學(xué)報(bào), 2009, 45 (12): 89-94.
Ding Feng, He Zhengjia, Zi Yanyang, et al. Reliability assessment based on equipment condition vibration feature using proportional hazards model [J]. Chinese Journal of Mechanical Engineering, 2009, 45 (12): 89-94. (in Chinese)
[7] Zhang Chao, Wang Shaoping, Bai Guanghan.An accelerated life test model for solid lubricated bearings based on dependence analysis and proportional hazard effect[J].Acta Astronautica,2014,95(1): 30-36.
[8] Zhang Qing, Hua Cheng, Xu Guanghua. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data [J]. Mechanical Systems and Signal Processing, 2014, 43 (1-2): 103-112.
[9] Janjarasjitt S, Ocak H, Loparo K. Bearing condition diagnosis and prognosis using applied nonlinear dynamical analysis of machine vibration signal [J]. Journal of Sound and Vibration, 2008, 317 (1-2): 112-126.
[10]Scholkopf B, Smola A, Muller k R. Nonlinear component analysis as a kernel eigenvalue problem [J].Neural Computation,1998, 10 (5): 1299-1319.
[11]Liu Wenbin, He Yuxin, Wang Huaqing, et al. Bearing condition recognition based on kernel principal component analysis and genetic programming [J].Applied Mechanics and Materials, 2013, 397-400(1): 1282-1285.
[12]李巍華,廖廣蘭,史鐵林. 核函數(shù)主元分析及其在齒輪故障診斷中的應(yīng)用[J]. 機(jī)械工程學(xué)報(bào),2003(8):65-70.
Li Weihua, Liao Guanglan, Shi Tielin. Kernel principal component analysis and its application in gear fault diagnosis [J]. Chinese Journal of Mechanical Engineering,2003(8):65-70.(in Chinese)
[13]Lee J, Yoo C, Choi S, et al. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59 (1):223-234.
[14]He Qingbo, Yan Ruiqiang, Kong Fanrang, et al. Machine condition monitoring using principal component representations [J]. Mechanical Systems and Signal Processing, 2009, 29 (2): 446-466.
[15]胡金海,謝壽生, 侯勝利,等. 核函數(shù)主元分析及其在故障特征提取中的應(yīng)用[J]. 振動(dòng)、測(cè)試與診斷, 2007, 27 (1): 48-52.
Hu Jinhai, Xie Shousheng, Hou Shengli, et al. Kernel principal component analysis and its application to fault feature extraction [J] Journal of Vibration, Measurement & Diagnosis, 2007, 27 (1): 48-52. (in Chinese)
[16]李學(xué)軍,李平, 蔣玲莉,等. 類均值核主元分析法及在故障診斷中的應(yīng)用[J]. 機(jī)械工程學(xué)報(bào), 2004, 50 (3): 123-129.
Li Xuejun, Li Ping, Jiang Lingli, et al.Class mean kernel principal component analysis and its application in fault diagnosis [J]. Chinese Journal of Mechanical Engineering, 2004, 50 (3): 123-129. (in Chinese)
[17]王新峰,邱靜,劉冠軍. 核主元分析中核函數(shù)參數(shù)選優(yōu)方法研究[J]. 振動(dòng)、測(cè)試與診斷, 2007, 27 (1):62-64.
Wang Xinfeng, Qiu Jing, Liu Guanjin. The study on the parameter selection of kernel function in kernel principal component analysis [J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27 (1):62-64. (in Chinese)
[18]Lagarias J, Reeds J, Wright M, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions [J]. Society for Industrial and Applied Mathematics Journal on Optimization, 1998, 9 (1): 112-147.
[19]Qiu Hai,Lee J A Y, Lin Jiang, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics [J]. Journal of Sound and Vibration, 2006, 289 (4-5): 1066-1090.
[20]Wang Fengtao, Sun Jian, Yan Dawen. A feature extraction method for fault classification of rolling bearing based on PCA [J].Journal of Physics: Conference Series, 2015, 628(1):1-7.
[21]蘇文勝,王奉濤,朱泓,等. 基于小波包樣本熵的滾動(dòng)軸承故障特征提取[J]. 振動(dòng)、測(cè)試與診斷, 2011,31(2) :162-166.
Su Wensheng, Wang Fengtao, Zhu Hong, et al. Study on the feature extraction of rolling element bearing fault based on wavelet packet sample entropy [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 162-166. (in Chinese)
[22]Williams T, Ribadeneira X, Billington S, et al. Rolling element bearing diagnostics in run-to-failure lifetime testing [J].Mechanical Systems and Signal Processing, 2001, 15(5): 979-993.
[23]張志華. 可靠性理論及工程應(yīng)用[M]. 北京: 科學(xué)出版社, 2012: 9-10.

10.16450/j.cnki.issn.1004-6801.2017.03.009
國家自然科學(xué)基金資助項(xiàng)目(51375067);航空科學(xué)基金資助項(xiàng)目(20132163010)
2016-12-30;
2017-03-15
TH165.3; TH17
王奉濤,男,1974年2月生,博士、副教授。主要研究方向?yàn)樵O(shè)備狀態(tài)監(jiān)測(cè)與故障診斷、振動(dòng)與噪聲。曾發(fā)表《基于流形-奇異值熵的滾動(dòng)軸承故障特征提取》(《振動(dòng)、測(cè)試與診斷》2016年第36卷第2期)等論文。 E-mail:wangft@dlut.edu.cn

