多維性能極限狀態平面不規則結構易損性分析*
黃小寧, 杜永峰,2, 李 慧,2
(1.蘭州理工大學防震減災研究所 蘭州, 730050)(2.蘭州理工大學西部土木工程防災減災教育部工程研究中心 蘭州, 730050)
?
多維性能極限狀態平面不規則結構易損性分析*
黃小寧1, 杜永峰1,2, 李 慧1,2
(1.蘭州理工大學防震減災研究所 蘭州, 730050)(2.蘭州理工大學西部土木工程防災減災教育部工程研究中心 蘭州, 730050)
針對平面不規則框剪結構,在引入最不利輸入角度的基礎上,提出多維性能極限狀態的易損性分析方法。首先,利用Matlab中小波變換系數法,判別地震動的最不利輸入方向;然后,采用層間位移和層間扭轉角作為性能量化指標并考慮量化指標間的相關性,計算超越概率,從而得到二維性能極限狀態下結構的易損性曲線。利用該方法對平面不規則框剪結構進行分析得到結構在正常使用、可以使用、生命安全、防止倒塌4個性能水平下的易損性曲線。結果表明:對于平面不規則結構,地震動輸入角度對結構的抗震性能有不可忽略的影響;對平面不規則結構進行易損性分析時,應同時考慮層間位移和層間扭轉角雙指標的影響,防止高估這類結構的抗震性能。基于多維性能極限狀態的易損性分析方法對平面不規則結構抗震性能的評估更為安全、可靠。
平面不規則結構;易損性分析;多維性能極限狀態;層間位移;層間扭轉角
引 言
水平地震作用下,平面不規則結構的豎向構件可能處于壓、彎、剪、扭的復雜受力狀態,對該類結構的抗震性能帶來不利的影響。因此,研究平面不規則結構在平動與扭轉同時存在時的抗震性能有重要的意義。對建筑物進行地震易損性分析,可以評估結構在不同地震動作用下的抗震性能,既可以有針對性的提高結構的抗震性能,又能為地震損失估計提供依據[1-3]。劉晶波等[4]提出了一種基于性能的結構整體地震易損性分析方法,該方法可全面考慮結構與地震動的不確定性,從性能的角度評估結構的抗震性能。徐強等[5]以損傷指數為指標,對防屈曲支撐鋼框架進行易損性分析。 Cimellaro等[6]以加速度和層間位移為指標提出了基于多維性能極限狀態結構的易損性分析方法。以上研究均沒有考慮結構扭轉響應對結構易損性的影響,在歷次強烈地震震害調查中發現,扭轉響應同樣可能導致建筑物的破壞。因此,筆者在此基礎上,提出以層間位移與層間扭轉角為指標,多維性能極限狀態平面不規則結構的易損性分析方法,利用Matlab中小波變換系數法,確定地震動最不利輸入方向來模擬不同輸入角度對結構響應的影響[7]。以層間位移和層間扭轉角作為性能量化指標,推導得到結構在正常使用、可以使用、生命安全、防止倒塌4個性能水平下的易損性曲線,評估結構在不同等級地震作用下的抗震性能。
1 小波變換在平面不規則結構地震反應分析中的應用思路
何曉宇等[8]提出利用小波變換系數法得到地震波與結構基頻相對應的頻率能量的大小,從而確定結構的最不利輸入方向。
根據以上思想確定平面不規則結構,地震動最不利輸入方向的步驟如下:
1) 選取雙向地震動,并根據入射角分解為xθ和yθ,如圖1所示;
2) 對xθ和yθ進行小波變換;
3) 從小波系數圖譜中提取與結構質量參與系數達90%時參與模態的頻率所對應的小波系數曲線,將各階頻率對應的“有效輸入能量”之和作為該角度下地震動的“有效輸入能量”,定義有效輸入能量為所對應的小波系數曲線與時間軸所圍的面積;
4) 選取“有效輸入能量”最大的入射角作為結構增量動力(increment dynamic analysis,簡稱IDA)分析時地震動入射角。
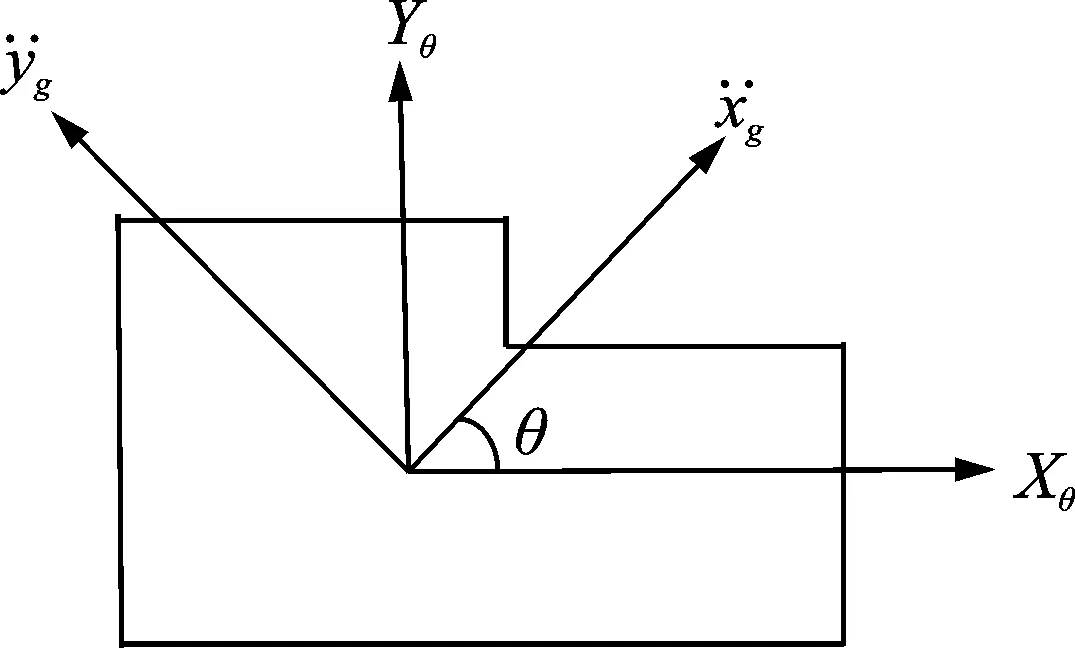
圖1 地震入射角的定義Fig.1 Definition of the incident angle
2 基于多維性能指標結構易損性分析方法
2.1 易損性分析方程
以多維性能指標定義的易損性方程可表示為
(1)
其中:Ri為結構的響應;rLSi為結構極限破壞狀態界限值;I為地震動強度等級。
2.1.1 單指標易損性分析方程
當僅考慮單指標(層間位移或層間位移角)時,其易損性方程可表示為
(2)
其中:D為結構層間位移響應;DLSi為第i個性能水平下結構層間位移極限破壞狀態界限值。
當極限破壞狀態界限值為定值時,結構的超越概率可表示為
(3)
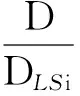
(4)
其中:μD為層間位移響應均值;μDLSi為第i個性能水平下層間位移極限破壞狀態界限值的均值;σlnD為層間位移響應的對數標準差;σlnDLSi為第i個性能水平下層間位移極限破壞狀態界限值的對數標準差。
2.1.2 雙指標易損性分析方程
當考慮層間位移和層間扭轉角作為結構的性能指標時,其易損性方程可表示為
(5)
其中:θT為層間扭轉角響應;ΔTLSi為第i個性能水平下結構層間扭轉角極限破壞狀態界限值。
當DLSi和ΔTLSi為固定值,D≥DLSi和θT≥ΔTLSi是兩個獨立事件時,則其超越概率可表示為
(6)
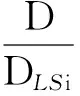
(7)
其中:μμθT為層間位移響應均值;μΔTLSi為第i個性能水平下層間位移極限破壞狀態界限值的均值;σlnθT為層間位移響應的對數標準差;σlnΔTLSi為第i個性能水平下層間位移極限破壞狀態界限值的對數標準差。
2.1.3 超越概率計算方法(多維性能指標相關)
文獻[6]提出易損性評估中各性能極限狀態相關時,構造多維性能極限狀態廣義方程為
(8)
根據式(8),當DLSi和ΔTLSi為相關變量時,其二維性能極限狀態方程為
(9)
其中:DaLSi,ΔaTLSi分別為考慮相關性情況下層間位移和層間扭轉角極限狀態;DLSi0,ΔTLSi0為層間位移和層間扭轉角固定限值。
為簡化計算,假設ND=1 ,可得
(10)
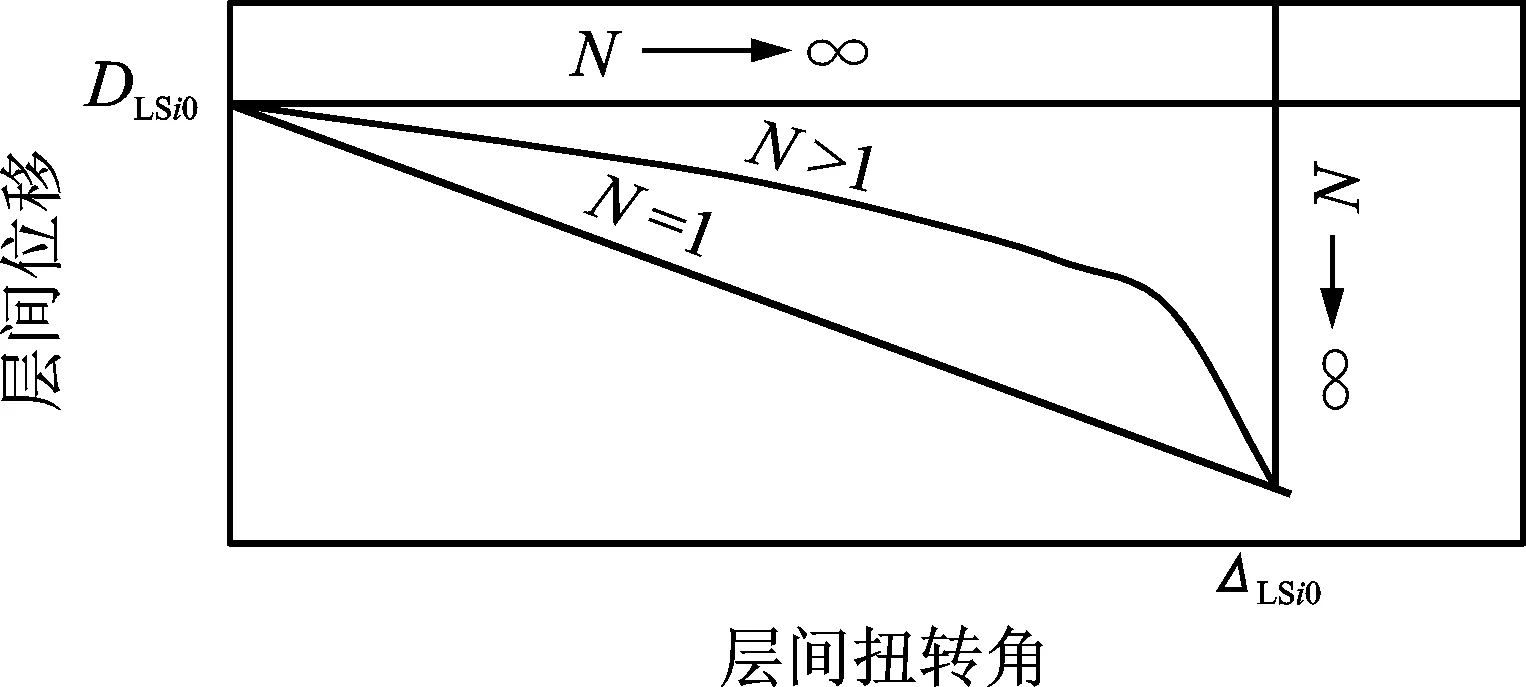
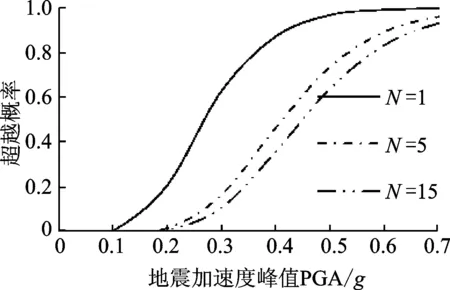
圖2 N 對二維性能極限狀態曲線的影響Fig.2 Bi-dimensional PLS for different value of N
N描述層間位移和層間扭轉角性能極限狀態的相關程度,確定二維性能極限狀態形狀,如圖2所示。由圖2可以看出,當N=1時,層間位移和層間扭轉角界限值線性相關,結構的失效面積最大,則在相同地震動作用下,結構的超越概率最大。隨著N的增大,在相同地震作用下,超越概率隨之變小。因此,忽略性能極限狀態相關性易損性估計偏低,導致結構抗震性能的高估,不利于工程安全。
筆者考慮層間位移響應和層間扭轉角響應服從二元對數正態分布的概率密度函數,如式(11)所示
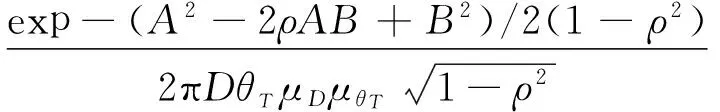
(11)
其中:A=[lnD-μD]/σD;B=[lnθT-μθT]/σθT;ρ為lnD和lnθT的相關系數。
由最大似然估計得到μD,μθT,σD,σθT及ρ,利用Matlab 編寫Monte Carlo模擬算法程序[9-10],隨機產生符合式(11)的隨機向量,統計落入式(10)范圍外的隨機向量個數,由此得到結構不同性能水平下的超越概率。
2.2 結構性能水平的確定方法
參照我國《建筑抗震設計規范》[11]及FEMA445[12]關于結構性能水平的劃分,本研究規定結構的抗震性能水平為正常使用(NO)、可以使用(IO)、生命安全(LF)和防止倒塌(CP)4個性能水平。筆者采用層間位移和層間扭轉角來定義結構的破壞狀態,表1給出了結構性能水平及極限狀態界限值的表示符號。
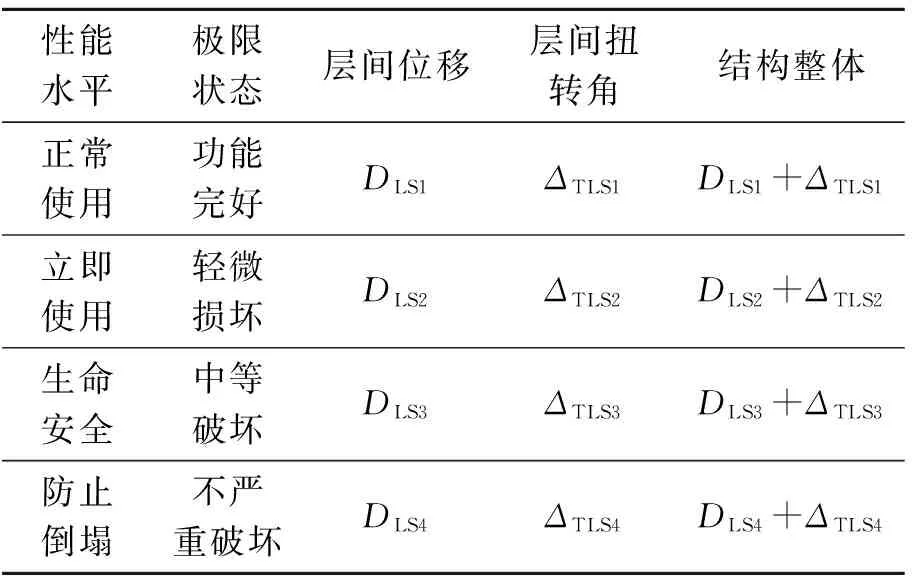
表1 結構整體性能水平
2.2.1 層間位移的量化指標
根據《建筑抗震設計規范》附錄M的條文說明中對層間位移角的相關規定及當取層高h=5.4m時,可知鋼筋混凝土框架-剪力墻結構豎向構件對應于不同破壞狀態的層間位移的界限值如表2所示。

表2 層間位移界限值
2.2.2 層間扭轉角的量化指標限值推導
根據《建筑抗震設計規范》,則有
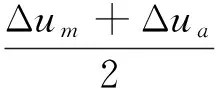
(12)
θT=(Δum-Δua)/R
(13)
其中:μ為結構的扭轉位移比;Δum為最大層間位移;Δua為平均層間位移;θT為層間扭轉角響應;R為該樓層柔性端到剛性端的距離。
由式(12)、式(13)推導可得

(14)
當分別取μ,Δum為《建筑抗震設計規范》中規定的相關限值時,式(14)可表示為
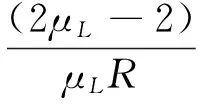
(15)
其中:μL為結構的扭轉位移比限值。
根據《建筑抗震設計規范》中對平面不規則結構的扭轉位移比的相關規定,將μL的取值定為1.2,1.3,1.4及1.5這4個值,DLSi為表2中給定的層間位移界限值,ΔTLSi為層間扭轉位移角限值。根據式(15)及可得到最大層間扭轉角參考控制目標如表3所示。

表3 層間扭轉角界限值
3 算例分析
筆者以一平面不規則的8層框剪結構為例。該結構的抗震設防類別為乙類,抗震設防烈度8度(0.2g),設計地震分組第3組,場地類別為Ⅱ類。其結構平面如圖3所示,結構形式為鋼筋混凝土框架剪力墻結構。A-B軸處剪力墻厚為400mm,其余剪力墻厚均為300mm,結構基本參數如表4所示。根據使用功能的要求,第8層層高5.4m,其余層均為3.9m。利用perform-3D對結構進行增量動力分析時,剪力墻用非彈性纖維截面,梁選用FAMA Beam, Concrete Type,柱選用FAMAColumn, Concrete Type來模擬構件的非線性行為。在ATC-63建議的地震動記錄集中選擇20條地震動,調幅至8個PGA(0.05g,0.1g,0.2g,0.3g,0.4g,0.5g,0.6g,0.7g) 作為地震激勵。

表4 結構基本參數
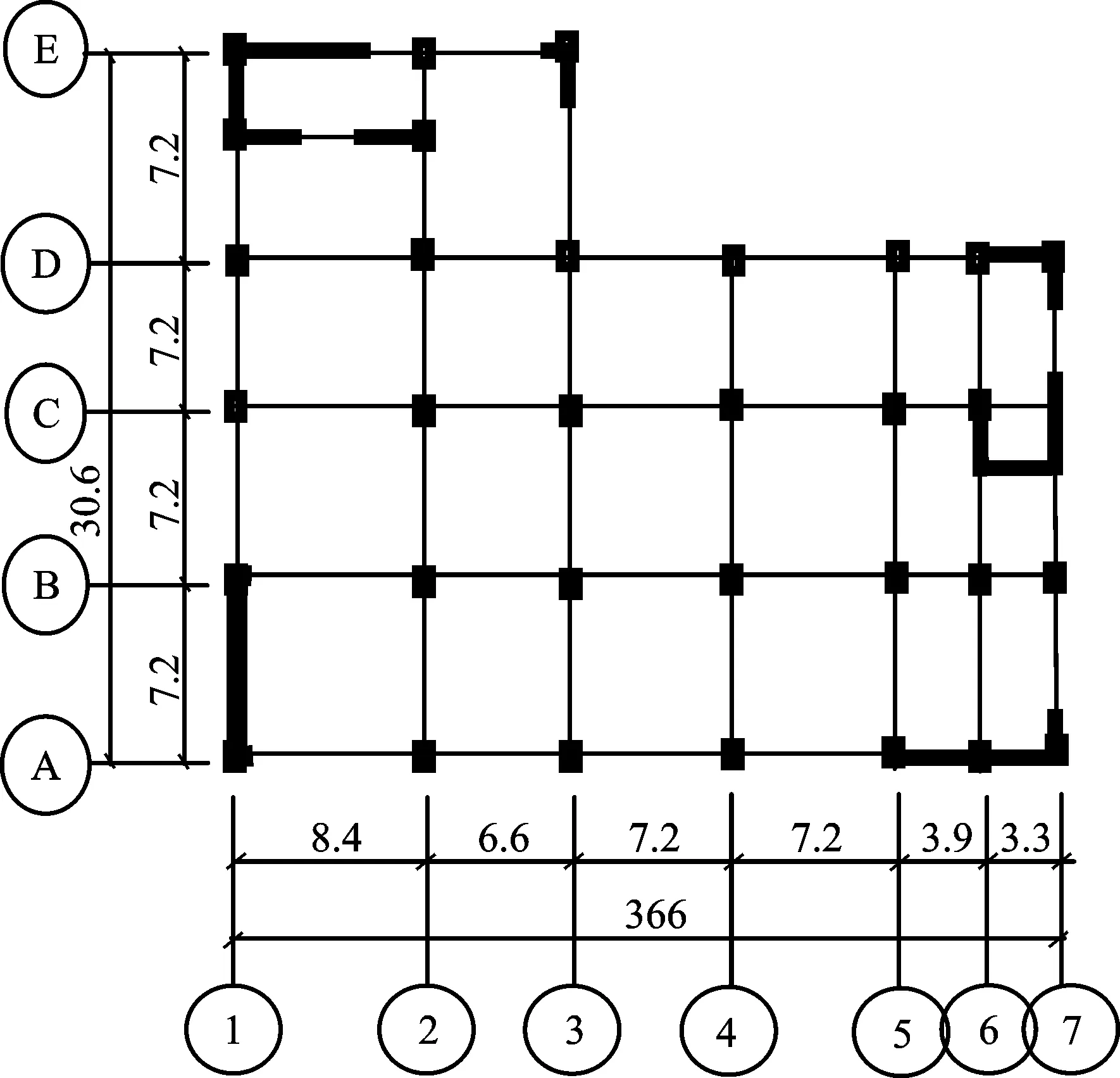
圖3 結構平面圖 (單位:m)Fig.3 Plan layout of structure (unit:m)
3.1 確定地震動最不利輸入角度
根據第1節中確定地震動最不利輸入角度的方法,可得到不同輸入角度的有效輸入能量。圖4為取PGA=400g時,Northridge-01沿00~1800x向“有效輸入能量”。圖5為利用perform3D進行非線性分析得到Northridge-01沿00~1800的地震動作用下x向的層間位移。
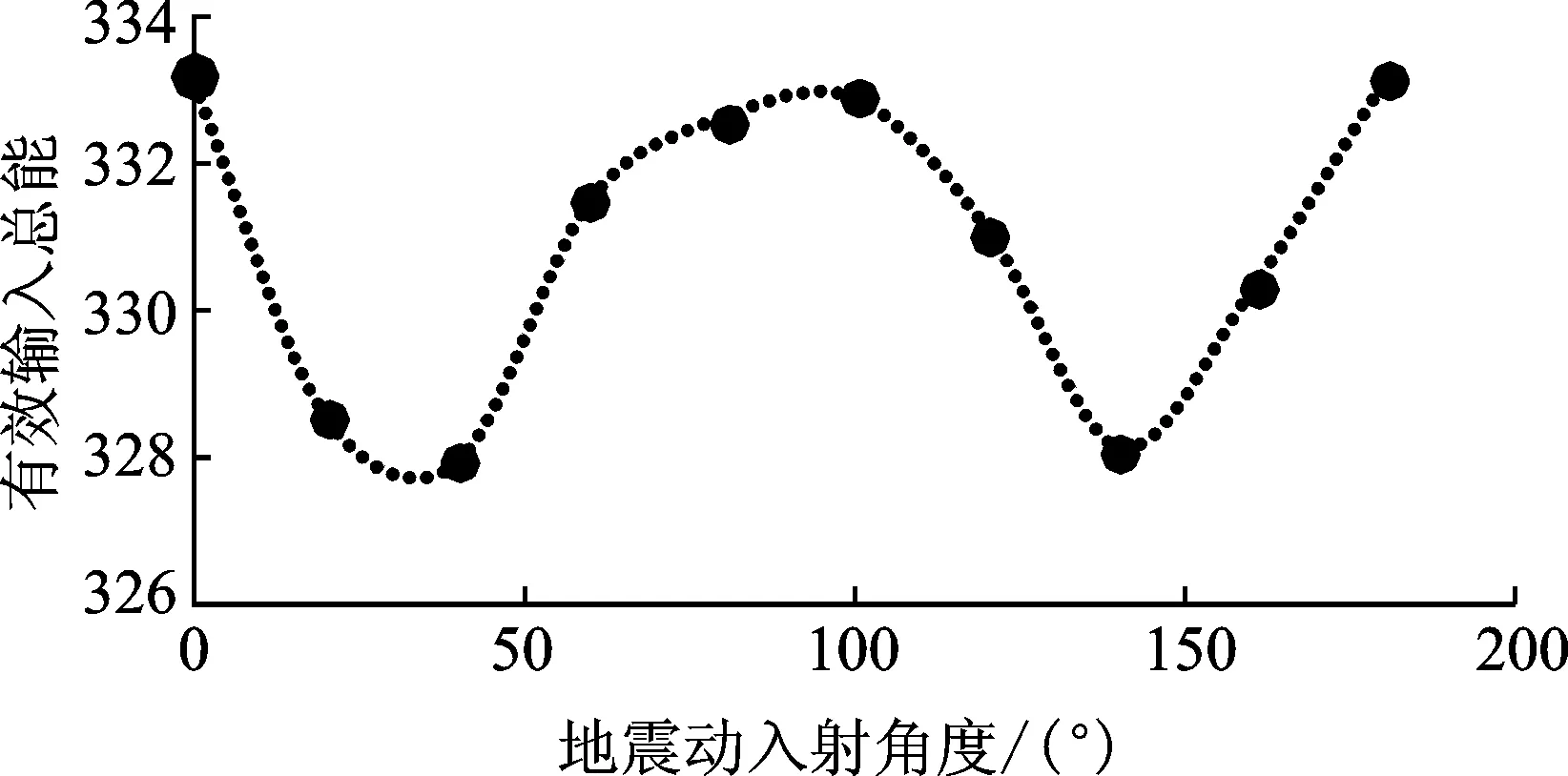
圖4 有效輸入能量與輸入角度關系曲線Fig.4 Relation curve of the effective energy and input angle
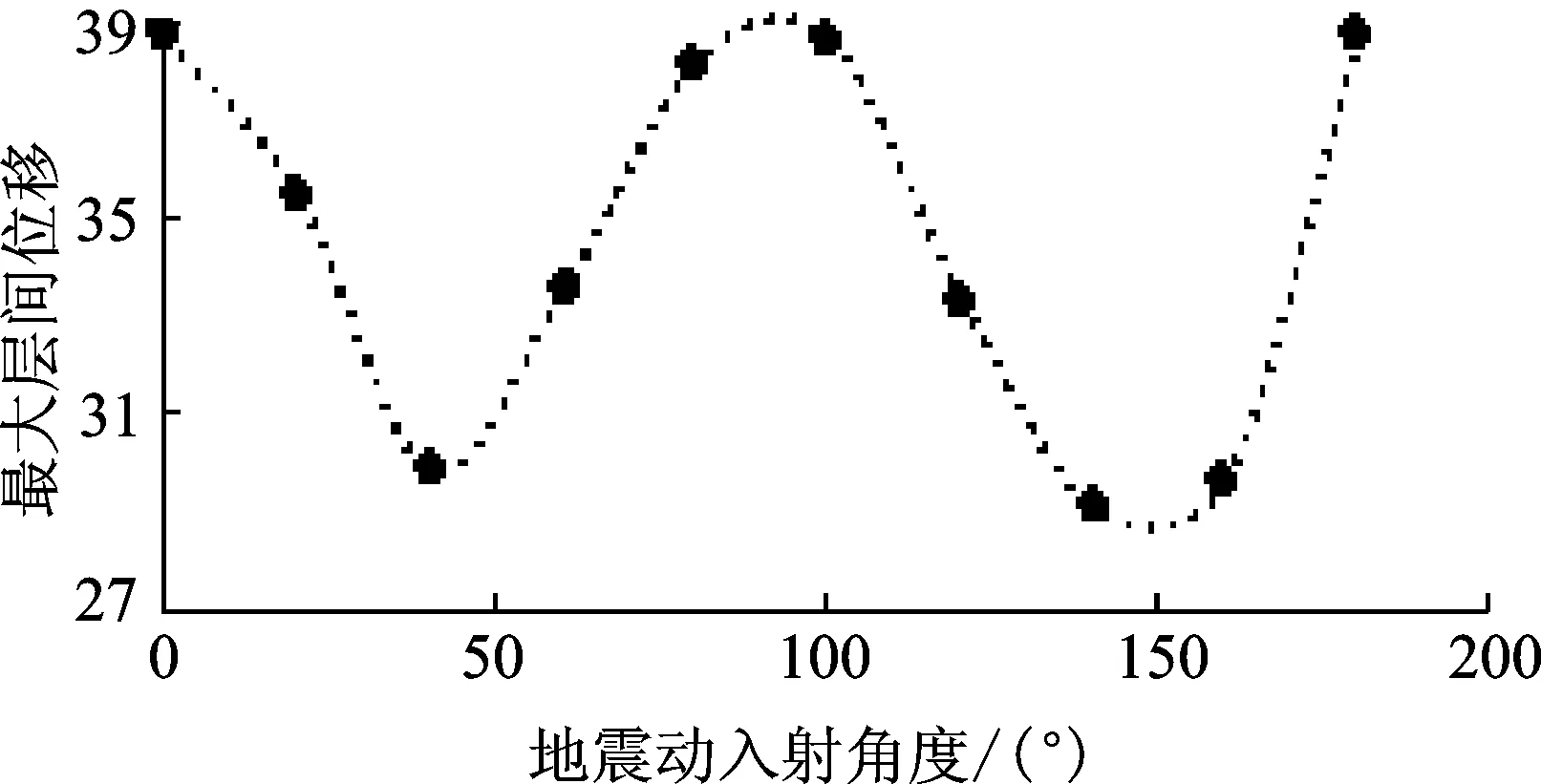
圖5 層間位移與輸入角度關系曲線Fig.5 Relation curve of inter-story drift and input angle
由圖4和圖5可以看出,沿x向地震波的“有效輸入能量”最大值出現在入射角為0°時。在perform3D中進行非線性時程分析時,沿x向的最大層間位移也出現在入射角為0°,且兩曲線的變化趨勢基本相似。這說明該方法可以用于計算平面不規則結構地震動的最不利輸入角度。由圖(5)可以看出,結構沿0°~180°輸入地震動時,最小層間位移為0.029 8m,最大層間位移為0.038 6m,增大將近30%。因此,地震動的輸入角度對于平面不規則結構的地震動響應有不可忽略的影響。
表5給出了筆者所選用的地震波的最不利輸入角度。根據所選用的地震波及每條地震波的最不利輸入角度,對選用的算例進行IDA分析。
3.2 基于單指標的結構易損性分析
考慮層間位移的極限破壞狀態界限值為固定值時,根據僅考慮單指標(層間位移或層間位移角)時,超越概率的計算方法如式(3)所示,結合表2得到結構的易損性曲線。下面以第8層易損性曲線為基礎展開討論,圖6為將層間位移作為量化指標得到的易損性曲線。
由圖6可以看出,結構正常使用極限狀態的易損性曲線比其他性能水平的易損性高, 說明結構在地震作用下超越正常使用性能水平的概率較大。隨著PGA的增大,易損性曲線逐漸下移,表明性能水平不同,相同地震動下,超越概率不同,防止倒塌極限狀態下的超越概率最小。

表5 選用的地震動的最大有效輸入能量
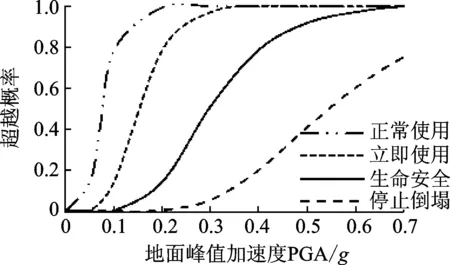
圖6 全局易損性曲線(單指標)Fig.6 Global fragility curves (an indicator)
當考慮層間扭轉角極限破壞狀態界限值為固定值時,根據僅考慮層間扭轉角時超越概率的計算方法如式(3)所示,結合表3可以得到結構的易損性曲線。當該結構的扭轉位移比限值μL分別為1.2,1.3,1.4,1.5時,第8層在防止倒塌性能下的層間扭轉角易損性曲線如圖7所示。
由圖7可以看出,在防止倒塌性能下,當扭轉位移比限值μL=1.2時,其超越概率最大,易損性曲線最高。隨著μL的增大,其超越概率減小,易損性曲線下移,說明在評估結構的抗震性能時,隨著μL的減小,評估結果越保守。因此,可以根據結構的性能需求提出適當的扭轉位移比限值,從而保證結構得到所需的抗震性能。

圖7 扭轉位移比對結構易損性的影響(單指標)Fig.7 Influence on fragility for torsional displacement ratio (an indicator)

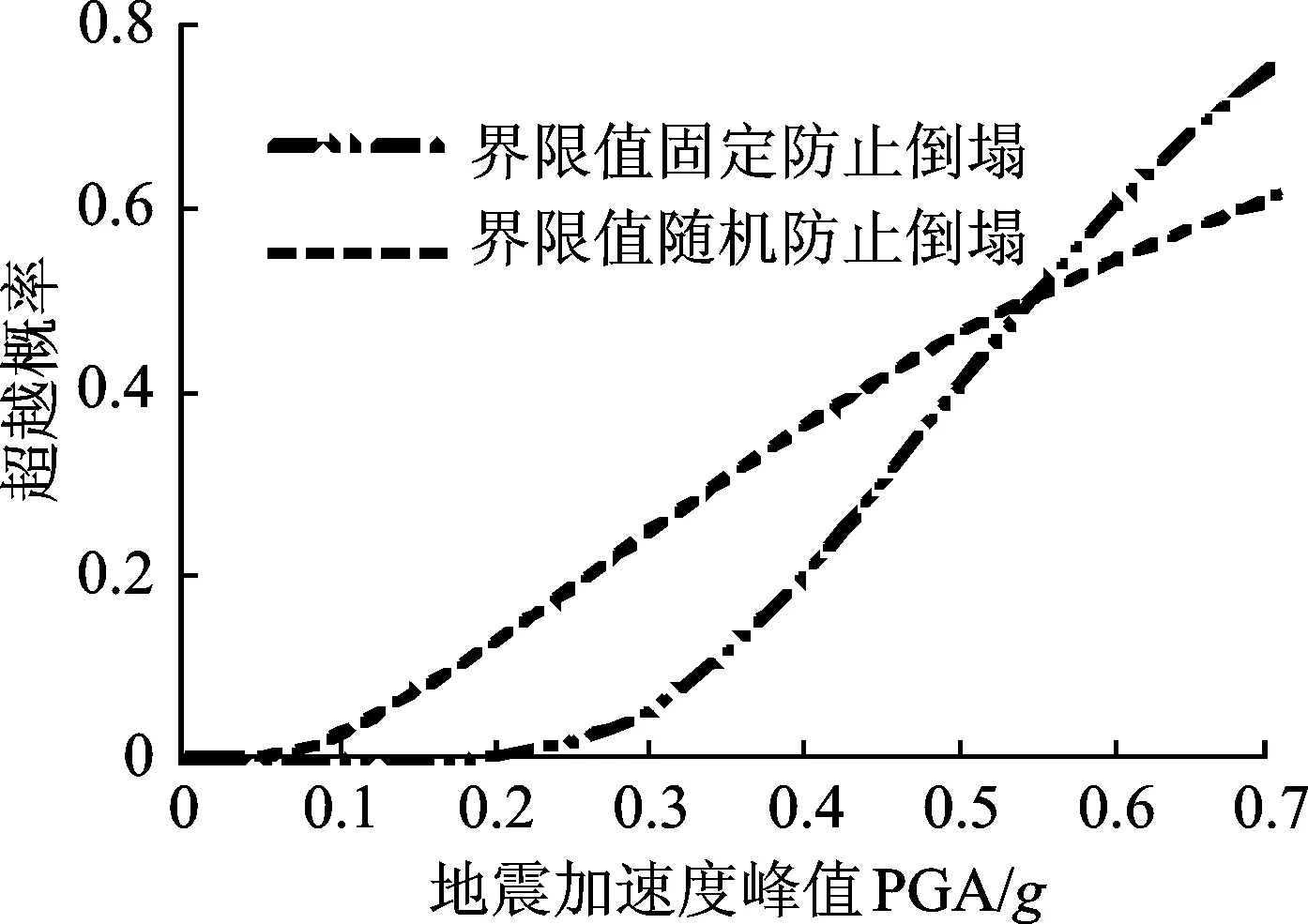
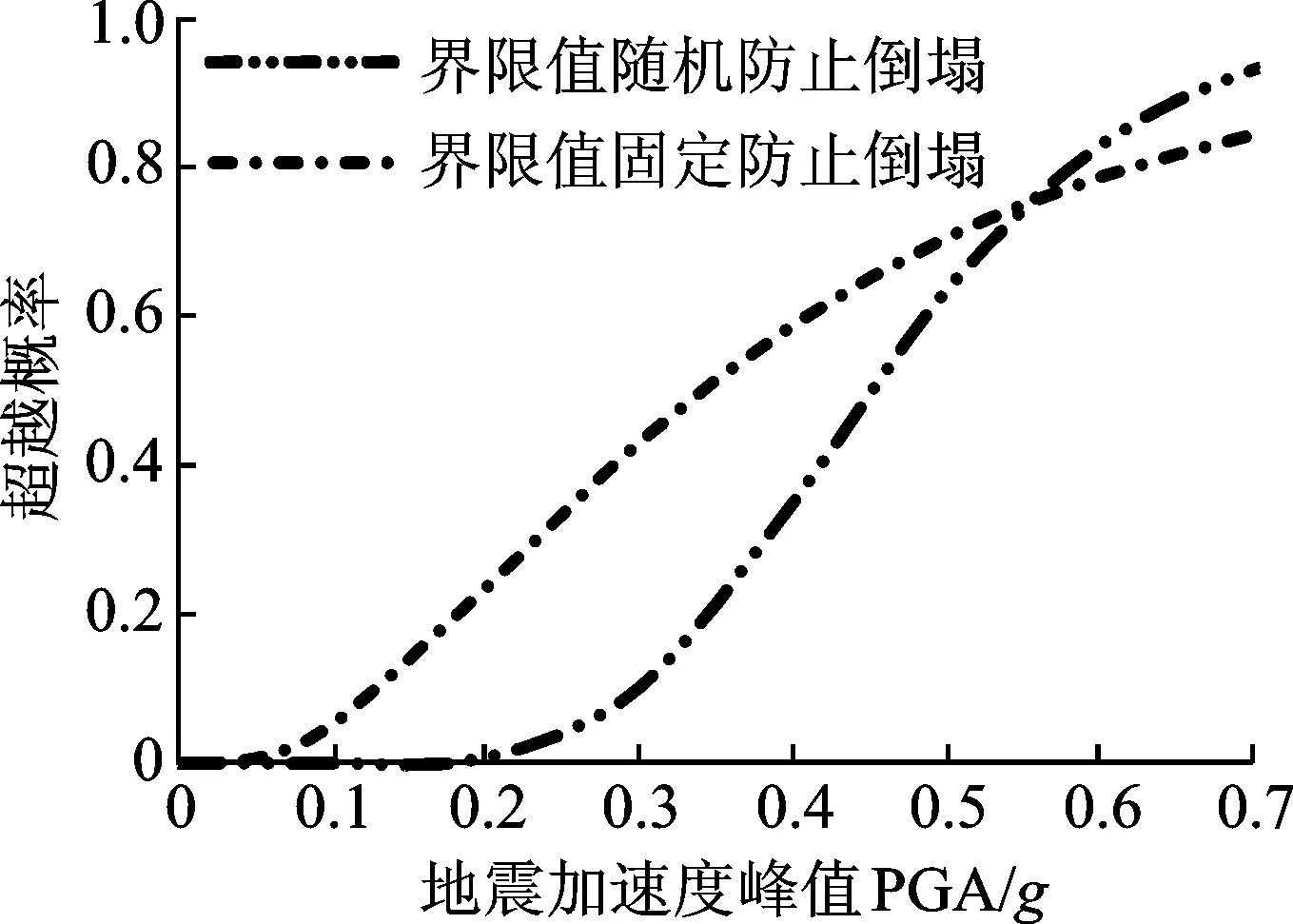
圖8 界限值隨機性對易損性的影響(單指標)Fig.8 Sensitivity of fragility to threshold randomness (an indicator)
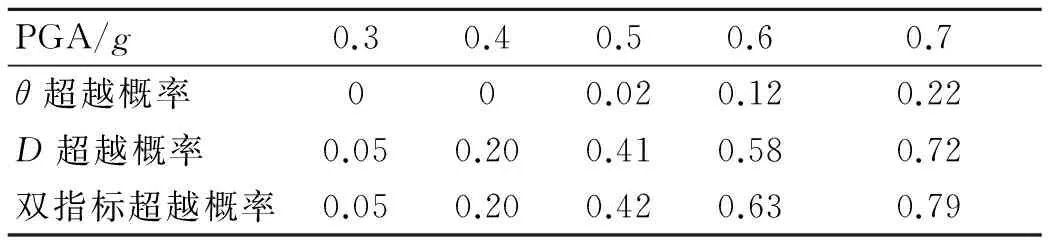
由圖8可以看出,當0(g) 3.3 基于雙指標的結構易損性分析 當DLSi和ΔTLSi為固定值時,取μL=1.4,由式(6)可以得到考慮雙指標界限值均為固定值時的超越概率,如圖9所示。表6為在地震動幅值相同時,以層間位移、層間扭轉角、層間位移和層間扭轉角為指標在防止倒塌性能下結構的超越概率的對比。 圖9 全局易損性曲線(雙指標)Fig.9 Global fragility curves (two indicators) PGA/g0.30.40.50.60.7θ超越概率000.020.120.22D超越概率0.050.200.410.580.72雙指標超越概率0.050.200.420.630.79 圖9為考慮結構的層間位移和層間扭轉角雙指標時,結構在4個性能水平下的易損性曲線。由圖9可以看出,結構正常使用極限狀態的易損性曲線最高,說明結構在地震作用下超越正常使用性能水平的概率較大,這與單指標得到的結論相似。從表6中可以看出,無論是單指標還是多指標,隨著地震動峰值的增大,超越概率增大。當地震動較大時,雙指標的超越概率大于單指標的超越概率,且隨著地震動峰值的增大;基于單指標的超越概率與基于雙指標的超越概率之間的差異也增大。 由圖10可以看出,當0(g) 圖10 界限值隨機性對易損性的影響(雙指標)Fig.10 Sensitivity of fragility to thresholds randomness (two indicators) 根據前面所述的性能指標相關時超越概率的計算方法,取μL=1.3,N=1,5,15,計算結構在防止倒塌性能下的超越概率,如圖11所示。 由圖11可以看出,N越大,二者趨于獨立。隨著N的減小,超越概率增大,易損性曲線上移。這與圖2得到的結論相符,即當N=1時超越概率最大,易損性曲線最高。隨著N的增大,易損性曲線下移且越接近性能指標相互獨立時評估結果。因此,當采用多維性能指標時,性能指標間的相關性不可忽略,且指標之間越趨于線性相關,評估結構越保守。 圖11 相關系數N對易損性的影響(雙指標)Fig.11 Sensitivity of fragility to interaction coefficient N(two indicators) 1) 引入地震動最不利輸入角可以真實且全面地模擬結構可能遭受的地震作用。從有效輸入總能量與入射角度關系曲線和層間位移與入射角度關系曲線比較可以看出,小波變換系數法可以用于計算平面不規則結構在地震作用下的最不利輸入角度。對于平面不規則結構而言,不同的輸入角度對結構響應的影響明顯,不可忽略。 2) 無論是單指標還是多指標,隨著地震動峰值的增大,超越概率增大。當地震動峰值較大時,雙指標的超越概率大于單指標的超越概率,且隨著地震動峰值的增大,單指標與雙指標之間的差異也增大。因此,對平面不規則結構進行易損性分析時,應同時考慮層間位移角和層間扭轉角雙指標的影響,防止高估這類結構的抗震性能。 3) 采用兩個性能量化指標進行易損性分析時,界限值的隨機性及性能指標之間的相關性會顯著影響結構的超越概率,在易損性分析時不可忽略。 [1] 何益斌,李艷,沈蒲生.基于性能的高層混合結構地震易損性分析[J].工程力學, 2013, 30(8):142-147. He Yibin, Li Yan, Shen Pusheng.Performance -based seismic fragility analysis of tall hybrid structures[J].Engineering Mechanics, 2013, 30(8):142-147.(in Chinese) [2] Goulet C A, Haselton C B, Mitrani-Reiser J, et al.Evaluation of the seismic performance of a code-conforming reinforced-concrete frame building from seismic hazard to collapse safety and economic losses earthquake engineering structural dynamics[J].Earthquake Engineering Structural, 2007, 36(13):1973-1997. [3] Williams R J, Gardoni P, Bracci J M, et al.Decision analysis for seismic retrofit of structures[J].Structural Safety, 2009, 31(2):188-196. [4] 劉晶波,劉陽冰,閆秋實,等.基于性能的方鋼管混凝土框架結構地震易損性分析[J].土木工程學報,2010, 43(2):39-47. Liu Jingbo, Liu Yangbing, Yan Qiushi, et al. Performance-based seismic fragility analysis of CFST frame structures[J].China Civil Engineering Journal, 2010, 43(2):39-47. (in Chinese) [5] 徐強,馬艷,王社良.基于構件損傷的防屈曲支撐鋼框架易損性分析[J].四川大學學報:工程科學版,2015,47(4):61-68. Xu Qiang, Ma Yan, Wang Sheliang. Vulnerability analysis of buckling-restrained brace frame based on the component damage [J]. Journal of Sichuan University : Engineering Science Edition,2015,47(4):61-68.(in Chinese) [6] Cimellaro G P, Reinhorn A M.Multidimensional performance limit state for hazard fragility functions[J].Journal of Engineering Mechanism, 2011, 137(1):47-60. [7] Lagaros N D. Multi-component incremental dynamic analysis considering variable incident angle [J].Structure and Infrastructure Engineering,2010,6:1-2,77 -94. [8] 何曉宇,李宏男.海洋平臺確定多維地震動最不利輸入方向的一種有效方法[J].振動與沖擊, 2007, 26(12):49-54. He Xiaoyu, Li Hongnan. Application of wavelet transform in muti-components seismic response of offshore platform[J].Journal of Vibration and Shock, 2007, 26(12):49-54.(in Chinese) [9] 王倩倩,張義民,王一冰,等. 復合隨機振動系統的動態可靠性分析[J].振動、測試與診斷,2013,33(4):670-675. Wang Qianqian , Zhang Yimin, Wang Yibing, et al. Dynamic reliability analysis of double random vibration system[J].Journal of Vibration, Measurement & Diagnosis, 2013,33(4):670-675. (in Chinese) [10]竇站,蔣軍成,朱常龍,等. 基于蒙特卡洛模擬算法的化工裝置失效概率估算[J].安全與環境學報,2012,12(6):161-164. Dou Zhan, Jiang Juncheng, Zhu Changlong, et al. Estimation of the chemical device failure probability based on Monte Carlo simulation algorithm [J]. Journal of Safety and Environment, 2012, 12(6):161-164. (in Chinese) [11]GB 50011—2010建筑結構抗震設計規范[S].北京: 中國建筑工業出版社, 2010. [12]FEMA445 Next-generation performance-based seismic design guidelines [S]. Washington D C: FEMA, 2006. [13]李剛,程耿東.基于性能的抗震設計—理論、方法與應用[M].北京:科學出版社,2004:24-75. 10.16450/j.cnki.issn.1004-6801.2017.03.022 國家自然科學基金資助項目(51578274;51178211) 2016-04-11; 2016-05-12 TU352.1+1 黃小寧,女,1988年3月生,博士生。主要研究方向為結構抗震性能評估。曾發表《平面規則RC框剪結構基于性能的減震設計方法》(《工程力學》2017年第34卷第3期)等論文。 E-mail:hxiaoning7191@163.com 通信作者簡介:杜永峰,男,1962年3月生,教授、博士生導師。主要研究方向為結構減震控制、結構健康監測等。 E-mail:dooyf@lut.cn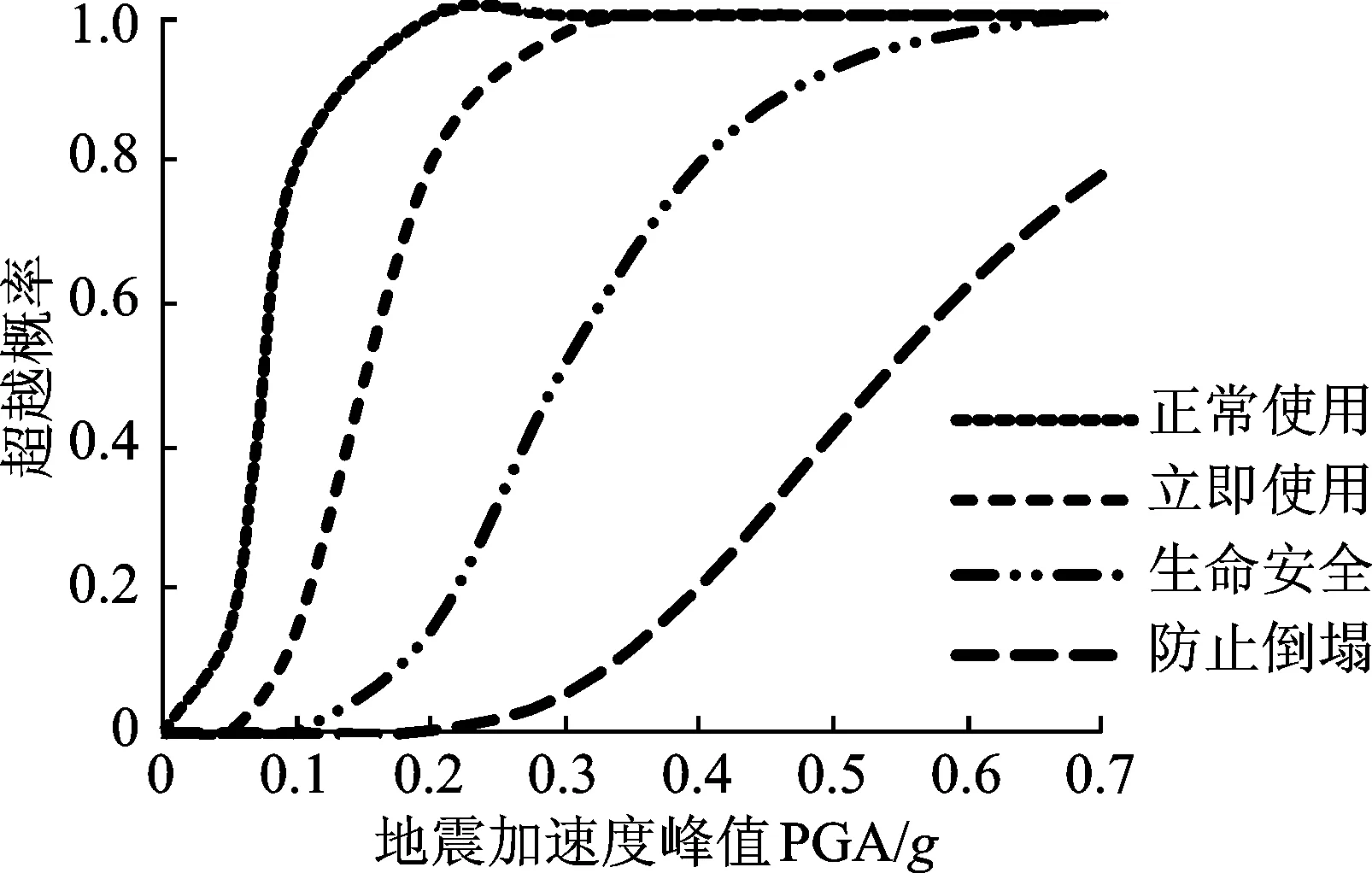
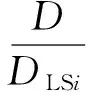
4 結 論


