斯特林發動機配氣活塞氣體的作用效應

李 薇, 牟 健, 洪國同

(1.中國科學院理化技術研究所 北京，100190) (2．中國科學院大學 北京，100049)

?

斯特林發動機配氣活塞氣體的作用效應

李 薇1,2, 牟 健1,2, 洪國同1

(1.中國科學院理化技術研究所 北京，100190) (2．中國科學院大學 北京，100049)

為了能夠深入認識自由活塞斯特林發動機配氣活塞的運動特性，對動力活塞固定不動時的配氣活塞的氣體作用效應進行了分析，并設計了配氣活塞的單獨運動實驗，在此基礎上提出了配氣活塞固有頻率的計算式。分析了工作腔壓力波超前與滯后配氣活塞位移兩種情況下受到的氣體力的作用情況，采用旋轉矢量法闡述了氣體力的作用機理。當壓力波超前或滯后活塞位移小于90°時，認為一部分氣體力發揮了氣體彈簧的作用，使系統固有頻率增大；當壓力波超前或滯后活塞位移大于90°但小于180°時，認為一部分氣體力發揮了慣性力的作用，使系統固有頻率減小。熱源溫度越高，系統的固有頻率越小。利用本實驗室的一臺自由活塞斯特林發動機進行實驗，驗證了上述氣體力作用的效應與規律，且利用此理論計算了系統固有頻率的準確性。

斯特林發動機； 自由活塞； 配氣活塞； 氣體作用效應； 固有頻率

引 言

隨著空間技術的發展，進入21世紀后，美國、俄羅斯、日本以及歐洲的主要航天大國紛紛提出了一系列深空探測的任務計劃，而這些計劃的實施也對空間電源提出了新的要求[1-3]。利用斯特林循環將熱能轉化為電能的自由活塞斯特林發電機，因其具有熱電轉化效率高、質量輕及體積小等優點，越來越受到航天大國們的重視，紛紛開展相關研究[4-7]。

自由活塞斯特林發動機是斯特林發動機的一種結構形式，其動力活塞和配氣活塞運動沒有機械結構的限制，因而被稱為“自由活塞”[8]。自由活塞斯特林發動機不僅具有傳統斯特林發動機理論效率高、外燃型等優點，還因為取消了傳統斯特林發動機的曲軸連桿結構，具有噪聲和振動小、壽命長等優點[9]。

對于自由活塞斯特林發動機而言，如果簡單地對發動機整機進行系統實驗，只能測試到整機的系統熱力學和動力學參數，而忽略了各部件的動力學特性及其相互之間的影響規律，相關的特性信息會被丟失，很難深入研究發動機的內在動力學特性、耦合過程及其對啟動運行的影響規律。筆者在對配氣活塞單獨進行動力學特性實驗研究的過程中，發現系統的固有頻率會隨著熱源溫度的升高而降低。由于固有頻率對改善系統穩定性和快速響應性起到至關重要的作用，長期以來一直被各行業作為研究的熱點問題[10-11]。對于自由活塞斯特林發動機而言，配氣活塞的固有頻率對整機的運行頻率起到關鍵性作用。針對這個問題，對配氣活塞振動系統的固有頻率進行了較深入的理論與實驗研究。

1 配氣活塞振動系統的動力學模型

配氣活塞單獨動力學實驗裝置由氣缸、配氣活塞、動力活塞、加熱器、回熱器、冷卻器和配氣活塞驅動電機等組成,具體結構如圖1所示。配氣活塞上端為熱腔，通過高溫換熱器與熱源(加熱棒)交換熱量。配氣活塞下端為冷腔，通過冷卻器向外界散熱。熱腔和冷腔之間通過回熱器連接，回熱器為環狀，位于配氣氣缸的外側，與其同軸。冷腔下端是動力活塞，動力活塞固定在實驗裝置缸體上，處于軸向某個位置，保持不動。動力活塞下端是緩沖腔，配氣活塞的驅動電機固定在緩沖腔內，通過配氣活塞桿(從動力活塞中間穿過)與配氣活塞相連。

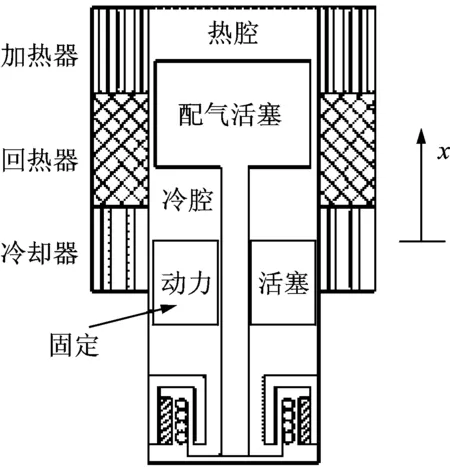
圖1 實驗裝置結構示意圖Fig.1 Schematic diagram of experimentalapparatus

自由活塞斯特林發動機配氣活塞的動力學模型可以用機械振動系統來詮釋，其受力分析如圖2所示。運動方程為

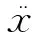
(1)

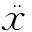
從式(1)可以看出，由于氣體力的出現，配氣活塞的運動方程不再是標準的阻尼受迫振動方程，配氣活塞的剛度也不再是單純的機械板彈簧剛度，氣體力在一定程度上表現出阻尼、彈簧與慣性的作用而影響配氣活塞的運動。所以，如何確定氣體力的作用效應就成為計算配氣活塞固有頻率的關鍵。

圖2 配氣活塞的受力示意圖Fig.2 Force diagram of displacer

由圖2可知，配氣活塞的氣體驅動力為

(2)

其中：Pe為熱腔壓力；Pc為冷腔壓力；Po為緩沖腔壓力；Ad為配氣活塞面積；Ar為配氣活塞桿面積；Ap為動力活塞面積(其中Ap=Ad-Ar)。

特殊地，當熱腔和冷腔的壓力相等時

Fd=(Ad-Ap)ΔP=ArΔP

(3)

從配氣活塞氣體驅動力的表達式可以看出，氣體驅動力與各個腔體的壓力、配氣活塞面積及配氣活塞桿的面積有關。當配氣活塞的結構參數一定時，各個腔體的壓力就決定了氣體驅動力的大小和方向。由于斯特林發動機在高低溫熱源間工作，工作腔內的壓力變化不僅與工作腔的體積變化有關，同時受到冷熱源溫度的影響。隨著冷熱腔溫度的變換，壓力波幅值和相位也會發生改變，氣體力對配氣活塞的作用效果也不同。下面就壓力波超前和滯后活塞位移兩種情況下的氣體壓力對配氣活塞的作用效應進行分析。

2 壓力波超前位移時的氣體作用效應

2.1 超前角度α≤90°

熱腔與冷腔壓力波超前配氣活塞位移角度小于90°時的氣體力的矢量圖如圖3所示。規定橫坐標為位移，并且橫坐標向左的方向為位移正方向。由于兩腔體的壓力波都超前活塞位移，且小于90°，所以冷腔的氣體作用力位于矢量圖的第三象限中。由于熱腔的壓力Pe對活塞的作用力與規定正方向的方向相反，所以轉動180°，位于矢量圖的第一象限中。配氣活塞最終受到的氣體作用力是兩腔體氣體力的合力。由圖3可知，熱腔的氣體作用力與冷腔的氣體作用力方向相反，所以合力的大小為兩腔體作用力的差值，正方向與熱腔氣體力的方向相同。

圖3 氣體力矢量圖(超前α≤90°)Fig.3 Vector diagram of gas force ( leading α≤90°)

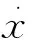
圖4 活塞受力的旋轉矢量圖(超前α≤90°)Fig.4 Rotation vector diagram of force on the displacer(leading α≤90°)

從圖4可知，氣體力可以分解為兩個力，一個是垂直于位移方向的氣體阻尼力，一個是平行于位移方向的氣體彈簧力。在特殊情況下，當α=0時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體彈簧力的作用；當α=90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到氣體阻尼力的作用。在熱腔與冷腔壓力波超前活塞位移角度小于90°的情況下，氣體阻尼的數值為

(4)

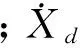
對于彈簧力而言，該情況可以認為機械板彈簧與氣體彈簧并聯，系統的總彈簧剛度等于板彈簧的彈簧剛度與氣體彈簧剛度相加。配氣活塞的固有頻率為

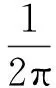
(5)

系統的總彈簧剛度為

k=(kdXd+Fdcosα)/Xd

(6)

氣體彈簧剛度為

kg=k-kd=Fdcosα/Xd

(7)

其中：Xd為配氣活塞位移的振幅。

2.2 超前角度90°<α≤180°

圖5為熱腔與冷腔壓力波超前配氣活塞位移角度大于90°但小于180°時的氣體力矢量圖，圖中依然規定橫坐標為位移，并且橫坐標向左的方向為位移正方向。由于兩腔體的壓力波都超前活塞位移，且大于90°，所以冷腔的氣體作用力位于矢量圖的第四象限中。由于熱腔的壓力Pe對活塞的作用力與規定正方向的方向相反，所以轉動180°，位于矢量圖的第二象限中。配氣活塞最終受到的氣體作用力大小同樣為兩腔體作用力的差值，正方向與熱腔氣體力的方向相同。

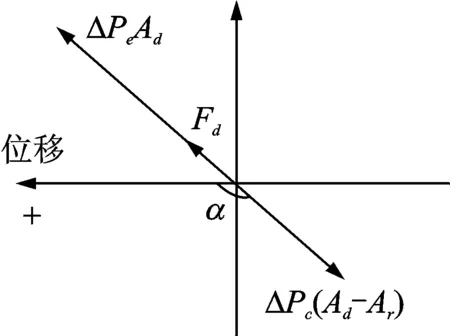
圖5 氣體力矢量圖(超前90°≤α≤180°)Fig.5 Vector diagram of gas force(leading 90°≤α≤180°)

圖6給出了熱腔與冷腔壓力波超前活塞位移角度大于90°但小于180°時的旋轉矢量圖。從圖6可知，氣體力同樣可以分解為兩個力，一個是垂直于位移方向的氣體阻尼力，一個是平行于位移方向的氣體慣性力。在計算配氣活塞的固有頻率時，需要將系統的動質量與氣體慣性力中的質量相加。特殊情況下，當α=90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到氣體阻尼力的作用；當α=180°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體慣性力的作用。

此時，配氣活塞的氣體阻尼和固有頻率仍然分別由式(4)和式(5)計算，系統的彈簧剛度僅為機械彈簧剛度，系統的總質量為

(8)

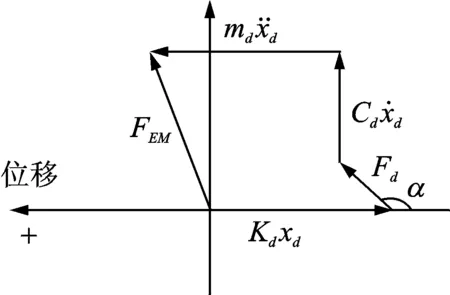
圖6 活塞受力的旋轉矢量圖(超前90°≤α≤180°)Fig.6 Rotation vector diagram of force on the displacer(leading 90°≤α≤180°)

3 壓力波滯后位移時的氣體作用效應

3.1 滯后角度α≤90°

熱腔與冷腔壓力波滯后活塞位移小于90°時的矢量圖如圖7所示。由于兩腔體的壓力波滯后活塞位移小于90°，所以冷腔的氣體作用力位于矢量圖的第二象限中。熱腔的壓力Pe對活塞的作用力與規定正方向的方向相反，位于矢量圖的第四象限中。配氣活塞最終受到的氣體作用力大小同樣為兩腔體作用力的差值，正方向與熱腔氣體力的方向相同。

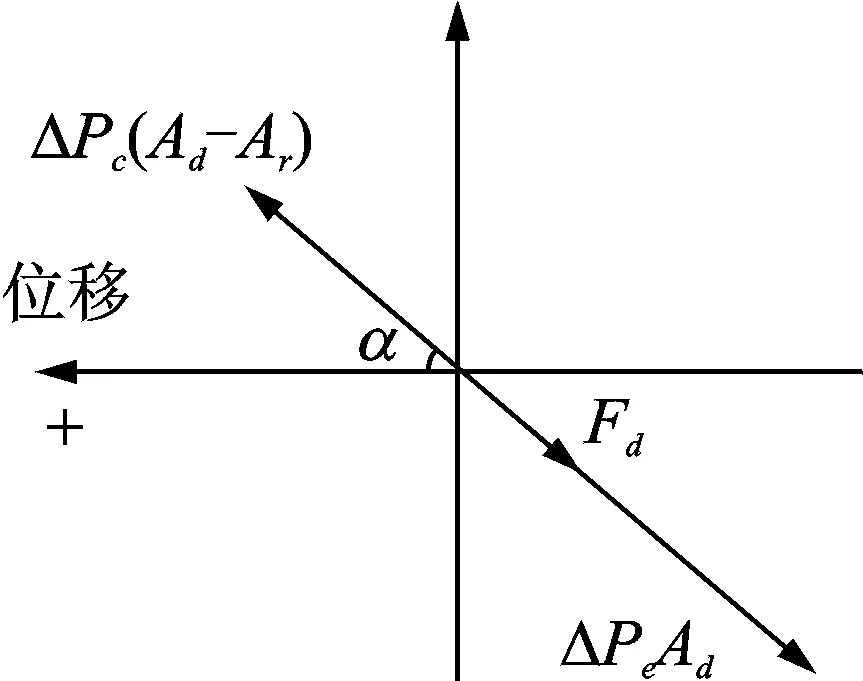
圖7 氣體力矢量圖(滯后α≤90°)Fig.7 Vector diagram of gas force ( lagging α≤90°)

圖8給出了熱腔與冷腔壓力波滯后活塞位移角度小于90°時的旋轉矢量圖。當其他參數不變時，氣體力分解為兩個力：a.垂直于位移方向、且與阻尼力方向相反的力；b.平行于位移方向的氣體彈簧力，氣體彈簧與機械彈簧并聯。此時，配氣活塞的氣體阻尼和固有頻率分別由式(4)和式(5)計算，系統總的彈簧剛度和氣體彈簧剛度分別采用式(6)和式(7)計算。

特殊情況下，當α=0時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體彈簧力的作用；當α=90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到抵制氣體阻尼力的作用。

圖8 活塞受力的旋轉矢量圖(滯后α≤90°)Fig.8 Rotation vector diagram of force on the displacer(laggingα≤90°)

3.2 滯后角度90°<α≤180°

熱腔與冷腔壓力波滯后活塞位移角度大于90°但小于180°時的氣體矢量圖如圖9所示。由于兩腔體的壓力波滯后活塞位移，且均大于90°，所以冷腔的氣體作用力位于矢量圖的第一象限中。熱腔的壓力Pe對活塞的作用力與規定正方向的方向相反，位于矢量圖的第三象限中。配氣活塞最終受到的氣體作用力大小同樣為兩腔體作用力的差值，正方向與熱腔氣體力的方向相同。

圖9 氣體力矢量圖(滯后90°≤α≤180°)Fig.9 Vector diagram of gas force (lagging 90°≤α≤180°)

圖10給出了熱腔與冷腔壓力波滯后活塞位移角度大于90°但小于180°時的旋轉矢量圖。當其他參數不變時，氣體力同樣分解為兩個力：a.垂直于位移方向、且與阻尼方向相反的力；b.平行于位移方向的氣體慣性力。此時，配氣活塞的氣體阻尼和固有頻率由式(4)和式(5)計算，系統的彈簧剛度僅為機械彈簧剛度，系統總質量包括氣體等效動質量，計算式為式(8)。

特殊情況下，當α=90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到抵制氣體阻尼力的作用；當α=180°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體慣性力的作用。

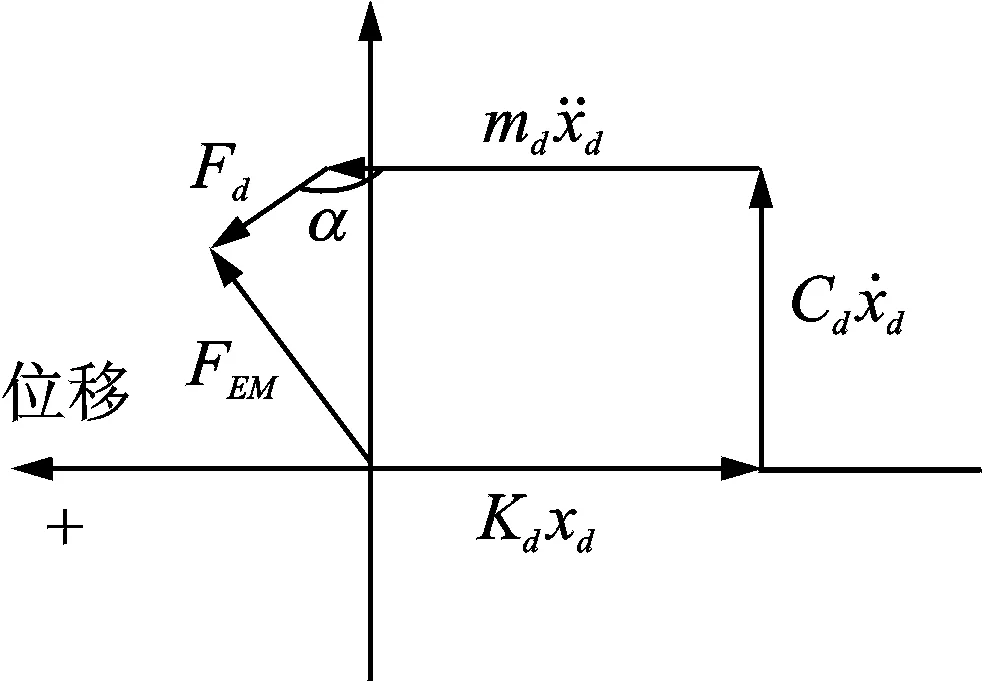
圖10 活塞受力的旋轉矢量圖(滯后90°≤α≤180°)Fig.10 Rotation vector diagram of force on the displacer(lagging 90°≤α≤180°)

4 實驗結果及分析

該實驗是在一臺輸出100W的自由活塞斯特林發動機上進行，實驗裝置通過位移傳感器和壓力傳感器獲得配氣活塞位移和冷熱腔壓力的實驗數據。將這些實驗數據代入式(2),(4),(6),(7),(8)及式(5)，計算得到氣體力、氣體阻尼系數、系統總的彈簧剛度、氣體彈簧剛度、系統總質量和系統固有頻率。同時采用共振法對系統進行實驗測得其系統的實際固有頻率，比較兩種固有頻率的大小以驗證上述氣體力作用效應理論的正確性。

實驗裝置的配氣活塞組件的運動質量為327g，板彈簧剛度為4 300N/m，充氣壓力為2MPa時，配氣活塞位移和冷熱腔壓力在不加熱與加熱兩種情況下的運行參數如表1所示。從表1可以看出，系統內不加入熱源時，冷熱腔體的壓力波幅值較小，且兩腔體的壓力波均超前活塞位移約20°；系統內加入熱源時，隨著熱源溫度的升高，冷熱腔的壓力波幅值逐漸增大，兩腔體的壓力波滯后活塞位移約150°。圖11給出了配氣活塞位移和冷熱腔壓力在不加熱與熱源溫度為500℃時的實驗曲線圖。

表1 不同熱源溫度下的運行參數

Tab．1 Operational parameters in different temperatures

熱源溫度/℃熱腔壓力幅值/MPa冷腔壓力幅值/MPaα/(°)位移幅值/mm270.02750.0260超前20.45.892000.05900.0570滯后170.85.993000.10100.0990滯后164.76.064000.11750.1150滯后155.05.985000.14200.1400滯后150.66.06

表2給出了不同熱源溫度時系統的機械阻尼、氣體阻尼和總阻尼系數。系統的機械阻尼是實驗裝置在真空條件下，采用激振的方法，得到活塞自由振動的衰減曲線，計算阻尼率，從而計算出活塞運動阻尼系數。氣體阻尼是由式(4)計算得到的。總阻尼是在不同熱源溫度下，利用激振法計算得到的。由表2可知，機械阻尼與氣體阻尼相加的數值要小于測得的總阻尼。同時，熱源溫度越高，氣體阻尼占總阻尼的比例越大，對總阻尼的影響也越大。

表2 不同熱源溫度下系統的阻尼值

Tab．2 Damping value under different temperatures of heat source

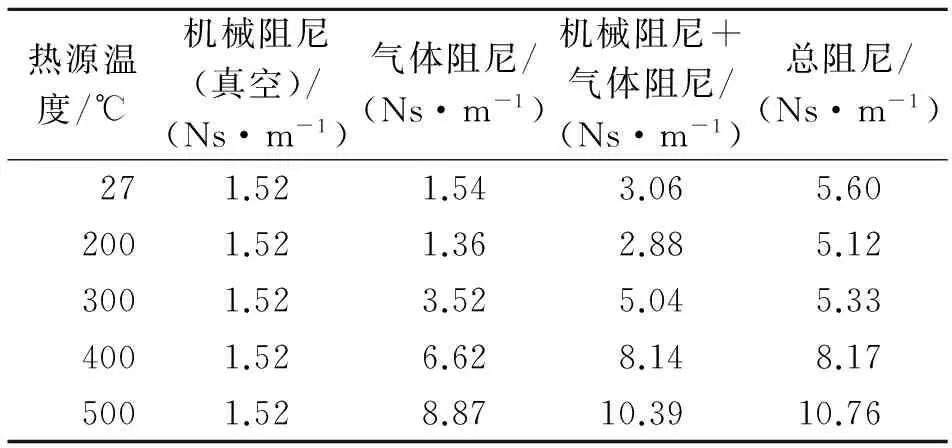
熱源溫度/℃機械阻尼(真空)/(Ns·m-1)氣體阻尼/(Ns·m-1)機械阻尼+氣體阻尼/(Ns·m-1)總阻尼/(Ns·m-1)271.521.543.065.602001.521.362.885.123001.523.525.045.334001.526.628.148.175001.528.8710.3910.76

表3不僅給出了系統剛度和固有頻率的計算結果，還根據阻尼固有頻率的計算表達式

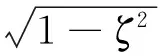
(9)

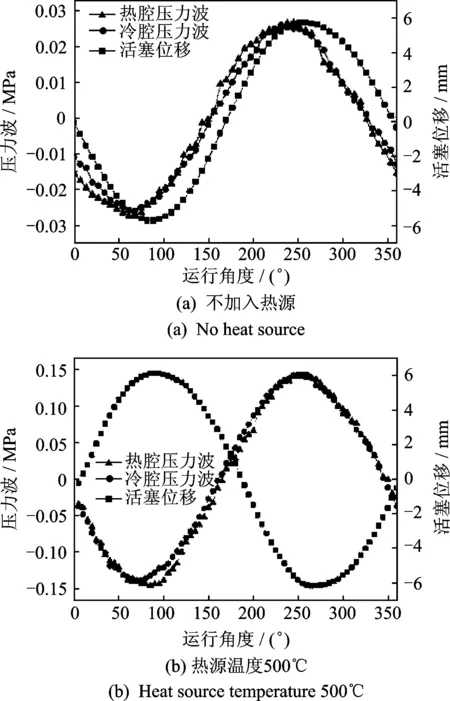
圖11 活塞位移和冷熱腔壓力在不加熱與加熱兩種情況下的實驗曲線Fig.11 Experimental data of displacement and pressure with and without heat sources

給出了不同熱源溫度下阻尼固有頻率的計算結果。從計算值可以看出，室溫下，由于壓力波超前位移處于0～90°之間，此時，氣體表現出氣體彈簧剛度特性，系統總的彈簧剛度增加，固有頻率比無氣體時的配氣活塞運動系統的大；隨著熱源溫度的升高，壓力波滯后活塞位移處于90°～180°之間，氣體表現出等效動質量特性，使得系統總的運動質量增加，整個系統的彈簧剛度和固有頻率逐漸減小，系統阻尼固有頻率變化不大，對整個振動系統的固有頻率幾乎沒有影響。

表3 不同熱源溫度下系統剛度和共振頻率的計算值

為了驗證上述理論的正確性，采用共振法對系統的固有頻率進行實際測量。測量時，保持電機驅動功率不變，只改變頻率，測量不同頻率下活塞的位移，位移最大時對應的頻率即為固有頻率。實驗測得不同加熱溫度下系統的固有頻率見表4。從表4可以看出，隨著熱源溫度的升高，系統固有頻率減小。

表4 不同熱源溫度下系統共振頻率的實驗值

Tab．4 Experimental values of the system resonance frequency under different temperatures heat source

熱源溫度/℃固有頻率/Hz27(真空)18.227(2MPa)18.820017.030015.940015.350014.6

將表3中固有頻率的計算值與表4中的實測值進行對比，可以發現計算值與實測值非常吻合，最大誤差僅為0.5 Hz,從而證明了所提出的固有頻率計算方法的正確性，也證明了配氣活塞存在明顯的氣體彈簧和氣體動質量作用效應，這種效應隨熱腔工作溫度的升高或冷熱源溫度差的增加而增大。

5 結 論

1) 當系統熱腔與冷腔壓力波超前或滯后配氣活塞位移角度α≤90°時，一部分氣體力起到了彈簧力的作用，系統總的彈簧剛度等于機械彈簧力與氣體彈簧力之和與位移的比值，此時認為氣體彈簧與機械彈簧并聯，系統總的彈簧力增大。

2) 當系統熱腔與冷腔壓力波超前或滯后活塞位移角度90°<α≤180°時，一部分氣體力起到了慣性力的作用，系統總的質量等于機械動質量與氣體等效動質量之和，系統總的慣性力增大。

3) 當系統熱腔與冷腔壓力波超前配氣活塞位移時，一部分氣體力表現為氣體阻尼作用，使得系統總的阻尼增大；當系統熱腔與冷腔壓力波滯后配氣活塞位移時，一部分氣體力則表現為氣體負阻尼作用，使得系統總的阻尼減小。

4) 對于自由活塞斯特林發動機而言，隨著熱源溫度的升高，壓力波滯后位移角度減少，氣體阻尼逐漸增大，氣體等效動質量也增大，系統固有頻率降低。

[1] Worms J C, Haerendel G. The european white paper on space: enough support for basic science?[J]. Space Policy, 2004, 20(2): 73-77.

[2] Zhou Yi. Perspectives on Sino-US cooperation in civil space programs[J]. Space Policy,2008,24(3):132-139. [3] Bignami G F. European vision for space science[J]. Space Research Today, 2005, 164: 8-15.

[4] Schock A, Or C, Kumar V. Radioisotope power system based on improved derivative of existing stirling engine and alternator[C]∥30th Intersociety Energy Conversion Engineering Conference. Orlando,FL,United States:[s.n.],1995．

[5] Or C, Kumar V, Carpenter R, et al. Self-supporting radioisotope generators with STC-55W stirling converters[J]. AIP Conference Proceedings,2000, 504(1): 1242-1251.

[6] Or C, Carpenter R, Schock A, et al. Performance of the preferred self-supporting radioisotope power system with STC 55-W stirling converters[J].AIP Conference Proceedings,2000, 504(1): 1252-1259.

[7] Cockfield R D. Radioisotope power system options for future planetary missions[J].AIP Conference Proceedings, 2001, 552(1): 740-746.

[8] G. 沃克.斯特林發動機[M]. 朱煒青，錢國柱，韓如，等譯.北京:機械工業出版社, 1987:2-3.

[9] 錢國柱. 熱氣機設計[M]. 北京：國防出版社，1987:7-19.

[10]上官文斌，陳超，段小成，等.發動機曲軸系統扭轉振動建模與實測分析[J].振動、測試與診斷,2012, 32(4):560-567.

Shangguan Wenbin,Chen Chao, Duan Xiaocheng, et al. Modeling and experimental analysis of torsional vibration in engine crankshaft syatem[J]. Journal of Vibration, Measurement& Diagnosis, 2012,32(4)：560-567.(in Chinese)

[11]王儼剴，馬進銳, 廖明夫，等.發動機振動趨勢預測模型研究[J].振動、測試與診斷，2014,34(3):516-523.

Wang Yankai, Ma Jinrui, Liao Mingfu, et al.Research on trend prediction model of engine vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(3)：516-523.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.023

2015-03-19；

2015-05-16

TH113.1； TK441+.1

李薇，女，1984年2月生，博士生。主要研究方向為自由活塞斯特林發動機動力學。曾發表《自由活塞斯特林發動機的間隙密封泄漏特性分析》(《真空與低溫》2012年第18卷第2期)等論文。 E-mail:liweitipc@163.com