三階非圓齒輪泵的流量脈動及可滾齒性研究

葉素娣，徐敬華

(1.蕪湖職業技術學院 電氣工程學院，安徽 蕪湖 241000；2.浙江大學 機械工程學院，浙江 杭州 310027)

三階非圓齒輪泵的流量脈動及可滾齒性研究

葉素娣1，徐敬華2

(1.蕪湖職業技術學院 電氣工程學院，安徽 蕪湖 241000；2.浙江大學 機械工程學院，浙江 杭州 310027)

隨著齒輪泵向高壓大流量低噪聲方向發展，提出了一種低困油、少脈動的非圓齒輪泵，并建立相應的節曲線模型。通過2個三階橢圓齒輪作為工作齒輪的情形(稱為3-3組合)、3個三階橢圓齒輪作為工作齒輪的情形(稱為3-3-3組合)在流量和流量脈動率方面的對比，確定3-3-3組合作為非圓齒輪泵的主要結構。非圓齒輪輪齒都有特定的嚙合位置，利用坐標變換法分析了非圓齒輪的齒廓方程，為CAD建模和仿真分析提供了理論依據。用圖形形式直觀地反映出不同階數非圓齒輪的凸性判別，得到三階非圓齒輪能用滾齒法加工的條件，為非圓齒輪的加工工藝路線明確了方向。

非圓齒輪；流量脈動；齒輪泵；齒廓方程；凸性判別

高壓大流量是齒輪泵發展的趨勢。傳統的由圓齒輪組成的齒輪泵在高壓下泄漏加劇，噪聲增強，效率降低[1]，因此研究少泄漏、低噪聲、高效率的容積泵十分重要，非圓齒輪泵應運而生。

非圓齒輪可實現周期性變速比運動，具有獨特的運動學、幾何學傳動特征，應用前景廣闊。文獻[2-6]研究了橢圓齒輪設計理論和傳動性能，提出諸多齒廓優化設計方法，包括用虛擬仿真設計非圓齒輪節曲線。

1 非圓齒輪的傳動比分析

圖1為一對非圓齒輪相互嚙合的節曲線，p為兩齒輪的中心距。

設主動齒輪的階數為n1，從動齒輪的階數為n2，n=n1/n2，則可寫出節曲線方程為：

(1)

(2)

本文中取n1=n2=3，即n=1。

r1+r2=p，由一對非圓齒輪傳動的封閉性條件即純滾動的條件，下式成立：

(3)

即中心距：

p=2a

(4)

根據齒輪傳動比的定義，得到一對同階非圓齒輪傳動比的表達式：

(5)

圖2為取階數n1=1，2，3時非圓齒輪的傳動比變化規律，圖3為階數n1=3時非圓齒輪副傳動比隨偏心率的變化規律。

由圖2、圖3可知，非圓齒輪的傳動比隨時間(主動輪轉角)周期性變化，周期為T=2π/n1。圖2中不同的階數有相同的幅值，說明幅值與階數無關；而圖3中偏心率越大幅值越大，說明幅值與偏心率有密切的關系。

2 兩個三階非圓齒輪組合泵的流量脈動分析

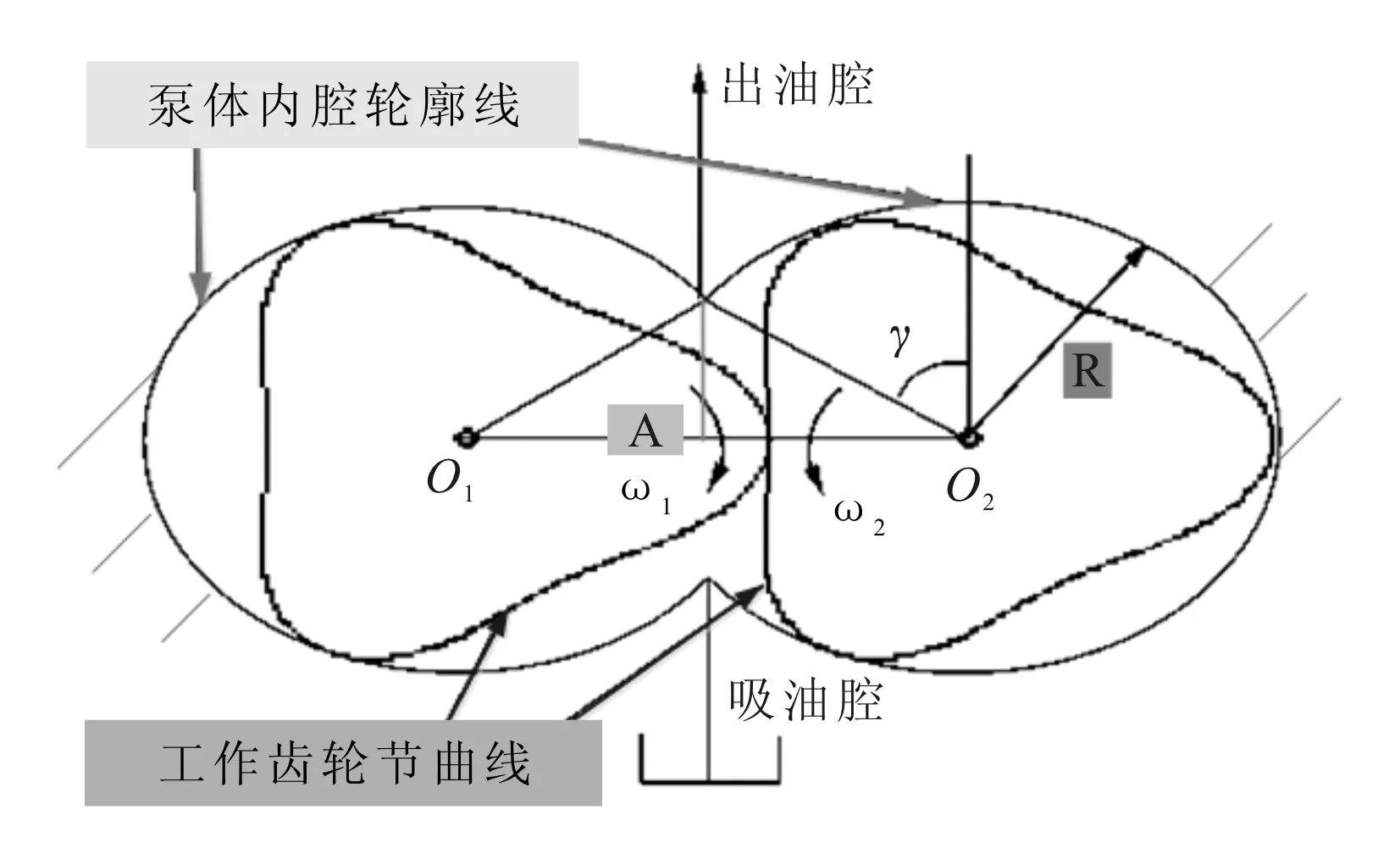
圖4 3-3組合非圓齒輪泵

一對三階非圓齒輪(簡稱3-3組合)的安裝如圖4所示，與泵體內腔輪廓線接觸的是齒輪節曲線，設泵體內腔半徑為R，則有R=r1max=r2max。

實際情況應是齒頂部分接觸(模數較小，齒頂高ha也較小，暫時可不考慮)。

任取一微段并積分，求得三階橢圓齒輪的面積S，具體公式如下：

(6)

設非圓齒輪泵的寬度為B，則在主動齒輪旋轉一周的過程中，密封腔容積的變化(即非圓齒輪泵的排量)為：

(7)

一對非圓齒輪滿足純滾動條件：φ1r1=φ2r2，則出油腔的容積變化量為：

(8)

代入(8)，整理后得到：

(9)

(10)

式中：ω1為主動齒輪1的勻角速度。

圖5所示為3-3組合在不同偏心率時，單位流量的變化規律。主動齒輪轉一周，流量有三次出現極大值和極小值，這是因為三階非圓齒輪的形狀是周期性對稱分布的；而偏心率越大，流量也越大，較大的偏心率意味著橢圓齒輪較扁平，封閉隔離區域的容積較大，故而流量較大。

設η為流量脈動率，則

(11)

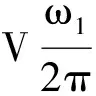
(12)

從公式(12)可知，流量脈動率與非圓齒輪的階數無關，只是偏心率的函數。圖6揭示了流量脈動率與偏心率的關系，當e=0.5時，η達到145%左右，由此在選擇非圓齒輪泵時，為減小流量波動，減小壓力波動，要盡量選取較小的偏心率。這與圖5得出的結論——只有較大的偏心率才有較大的流量，產生了矛盾，因此3-3組合的非圓齒輪泵有待改進。

如果有一種方法能使一組齒輪的最小流量和最大流量恰巧碰上另一組齒輪的最大流量和最小流量，這樣就能大大降低流量波動，而這種方法就是3-3-3組合。

3 三個三階非圓齒輪組合泵的流量脈動分析

在圖4的基礎上增加一個完全相同的三階非圓齒輪，組合成為3-3-3齒輪泵，見圖7所示。

主動輪與右從動輪形成3-3組合時，下腔為吸油腔，上腔為出油腔；主動輪與左從動輪形成3-3組合時，下腔為出油腔，上腔為吸油腔。將兩個吸油腔、兩個出油腔分別通過管路聯接，這樣在主動輪整周運動過程中，封閉隔離腔的容積和較大，同時容積變化較小，亦即流量較大但波動減小，脈動率降低[7-8]。

若主動輪與右從動輪的3-3組合的嚙合角為φ1，則與左從動輪的3-3組合的嚙合角為π+φ1，因此新增流量為：

(13)

3-3-3組合的總流量公式為：

QZ=Q+Q′

(14)

3-3-3組合在不同偏心率e時流量的變化規律如圖8所示。

3-3-3組合的流量變化周期為60°，在一個周期內最大流量和最小流量分別為：

(15)

(16)

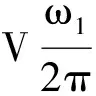
(17)

將圖9與圖6對比可以清楚地看出，3-3-3組合的流量脈動率遠遠低于3-3組合。

4 非圓齒輪齒廓設計及可滾齒性判別

(18)

以曲率半徑為當量圓齒輪的節圓半徑，則當量齒輪的基圓半徑ρ1=ρcos20°。

(19)

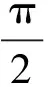
(20)

其中β=π-μ-φ1

以曲率中心M為原點，建立坐標系Mxmym，分別以ρ1和ρ為半徑畫基圓和節圓，并畫出一段漸開線，如圖11所示。

漸開線上任一點K的向徑為rK，壓力角為αk，展角為θk，分度圓上的展角為γ(γ=57.3°tan20°-20°) ，根據漸開線性質有：

γ=57.3°tan20°-20°

(21)

因此漸開線齒廓上一點在坐標系Oxy中的最終表達式為：

(22)

公式(22)可以形成非圓齒輪完整的齒廓。非圓齒輪的齒頂曲線和齒根曲線理論上是節曲線的法向等距線，它們與節曲線之間的法向距離分別是齒頂高ha、齒根高hf[9]。

非圓齒輪可以滾齒加工的條件是節曲線非內凹[10]，即ρ>0，將曲率半徑的分母作為判別式F，則F>0。

圖12為三階非圓齒輪的凸性判別，可以看出，三階非圓齒輪在偏心率e≤0.125時，齒輪的節曲線全部極角處F>0，能夠滾齒加工。而當偏心率e>0.125，齒輪的節曲線部分極角處F<0，不能滾齒加工。

圖13為不同階數非圓齒輪的凸性判別，由圖可以看出，當n=2，偏心率取至0.3時，齒輪的節曲線全部極角處F>0，能夠滾齒加工；n=4，偏心率取為0.1時，已有部分極角處F<0，即不顯示凸性，此時的非圓齒輪就不能通過滾制加工。

5 結語

(1) 3-3-3非圓齒輪組合相比3-3組合，具有流量大，脈動小的優點；

(2) 采用當量齒輪和坐標變換法，推導出非圓齒輪的齒廓方程，為三維建模和運動仿真提供了理論支持；

(3) 非圓齒輪的可滾齒性取決于階數和偏心率，當n≥4時，即使e=0.1，仍會有部分極角處不顯示凸性，不能用滾制方法加工成型；當n=3，偏心率≤0.125時，才能使齒輪節曲線的全部極角處都顯示凸性；而當n=2時，e≥0.3還能使齒輪節曲線的全部極角處都顯示凸性，能夠用滾齒法加工成型。

[1] 葉素娣,徐敬華.高壓大流量齒輪泵混合參數增效設計[J].機械科學與技術,2016,35(2):165-170.

[2] 張始齋,向毅,黃學滿,等.非圓行星齒輪液壓馬達節曲線的數值計算[J].機械設計,2013,30(4):37-39.

[3] 劉永平,孟鵬飛.基于MATLAB的高階橢圓齒輪副節曲線的設計[J].機械,2010,37(2):39-42.

[4] 黃志東,趙文珍.高階橢圓齒輪參數化建模與模態分析[J].制造業自動化,2015,37(23):8-12.

[5] 葉素娣,徐敬華.精密變位斜齒輪行星輪系混合型變量多目標優化設計[J].機械設計,2016,33(7):98-104.

[6] 李名堯,張猛,孫健.橢圓齒輪泵流量分析[J].上海工程技術大學學報,2009,23(1)：6-8.

[7] 譚偉明.高階橢圓齒輪多齒輪泵原理及其流量特性[J].機械傳動,2012,36(8):19-22,30.

[8] 丁凡,鄧民勝,劉碩,等.耐高壓雙向橢圓齒輪微小流量計研究[J].農業機械學報,2015,46(6):327-333.

[9] 柴樹峰,張學玲,李玉蘭.非圓齒輪設計及運動學仿真分析[J].軍事交通學院學報,2014,16(9):36-40.

[10] 張國政,韓江,劉有余.高階橢圓齒輪的滾齒加工方法及理論[J].計算機集成制造系統,2014,20(5):1106-1113.

[責任編輯、校對：梁春燕]

Research of Flow Pulsation & Gear Hobbing of Third-order Non-circular Gear Pumps

YESu-di1,XUJing-hua2

(1.School of Electrical Engineering, Wuhu Institute of Technology, Wuhu 241000,China; 2.School of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China)

With the development of gear pumps towards the direction of high pressure,high flow,and low noise,the paper presents a kind of non-circular gear pumps with low trapped oil and pulsation,and establishes the corresponding pitch-curve mode. By contrasting 3-3 combination with 3-3-3 combination in terms of flow and flow pulsation rate,the 3-3-3 combination is used as the main structure of non-circular gear pump.Coordinate transformation method is used to analyze the non-circular gear tooth profile equation, which provides a theoretical basis for establishing CAD modeling and simulation analysis.A graph is used to directly reflect the different order number convexity judging of non-circular gear,and obtain the conditions for the processing of three-order non-circular gears through the gear hobbing method,thus pointing out the direction for the technical route of non-circular gear processing.

non-circular gear;flow pulse;gear pump;tooth profile equation;convexity judging

2017-04-01

國家自然科學基金青年-面上連續資助項目(51005204，51375012)；浙江省自然科學基金資助項目(Y13E050014)；安徽省高校自然科研重點項目(KJ2017A553)；安徽省省級質量工程項目(2016ckjh227)

葉素娣(1969-)，女，浙江上虞人，副教授，工程師，主要從事CAD/CAE/CAM研究。

TH132.424

A

1008-9233(2017)03-0037-05