空間雙臂機器人運動學及動力學分析與建模研究

吳長征,劉殿富,岳 義，3,韋寶琛

(1.上海交通大學 機械系統與振動國家重點實驗室，上海 200240; 2.上海宇航系統工程研究所,上海 201109; 3.上海航天設備制造總廠,上海 200245)

?

空間雙臂機器人運動學及動力學分析與建模研究

吳長征1,劉殿富2,岳 義1，3,韋寶琛1

(1.上海交通大學 機械系統與振動國家重點實驗室，上海 200240; 2.上海宇航系統工程研究所,上海 201109; 3.上海航天設備制造總廠,上海 200245)

針對空間雙臂機器人運動學和動力學建模，對失重狀態下空間機器人的運動學分析與建模進行了研究。給出了雙臂機器人左右臂的DH坐標及參數，建立了正運動學的計算公式，基于臂形角的方法，給出了更高效的空間機器人冗余單臂的解析形式逆解求解方法。分析了空間雙臂機器人全部工作狀態，引入二元判定系數歸納得到了雙臂獨立運動、雙臂協同操作、閉鏈本體漂浮、開鏈本體漂浮4種四種機器人工作狀態，并基于拉格朗日方程得到了4種不同工作狀態下的動力學模型。通過對空間雙臂機器人運動學及動力學進行分析與建模，為空間雙臂機器人的設計與研究提供理論基礎。

空間雙臂機器人； 冗余； 解析形式； 逆運動學； 動力學； 失重； 建模； 判定系數

0 引言

空間機器人在在軌維護(如失效衛星捕捉、故障衛星修復)，代替航天員在危險復雜的太空環境中進行艙外作業、完成空間科學實驗，以及空間站的建設與維護等方面發揮了重要作用[1-2]。雙臂機器人的協作性能優良。但同時協作性能使其運動學及動力學具更強的耦合性和非線性。強耦合性和非線性導致其運動學及動力學模型更復雜。空間機器人的構型從最早期的單臂機器人Canadarm逐步發展到Dextre，Robonaut2等雙臂機器人，從而提高協作性能[3-5]。7自由度冗余機械臂因其避障、避關節極限、避關節奇異、最小化關節力矩、改善機械臂可操作度等的優勢，成為雙臂機器人臂型中最常用的類型[6-10]。

運動學逆解是運動學分析的重要內容，也是運動規劃及控制的基礎。針對冗余機械臂的運動學逆解解法進行了大量研究，但多是基于偽逆的方法，如加權雅可比、阻尼最小二乘法、梯度下降法等[7,11-12]。這些方法均是數值解法，且部分還加入了優化指標。基于偽逆的解法能針對不同的操作任務或操作指標進行優化，但求解效率及速度較低。文獻[13]提出了臂形角解法，引入臂形角約束獲得解析形式的逆解。解析型的解法則能極快得到解，但使機械臂失去了很多特性，如靈活性等。空間機器人工作時處于失重狀態，對機器人的動力學控制則需重新建立在失重環境中的動力學方程。建立動力學模型方法有拉格朗日方程、牛頓歐拉法、凱恩方程等[14]。拉格朗日法，只從能量的角度出發，通過對廣義坐標求導得到系統的廣義力；牛頓歐拉法通過分析每根桿件的受力情況建立迭代形式的動力學方程，易于計算機實現。上述方法，同樣適于空間機器人的動力學建模。針對特定自由漂浮狀態下的無根空間機器人系統，有虛擬機械臂、虛擬地面法、動力學等效法等[15]。本文針對基于偽逆的求解方法效率不高的問題，結合臂形角給出了空間雙臂機器人逆運動學解析形式求解方法，引入二元判定系數，將機器人的工作狀態歸納表示為4種不同工作狀態，針對4種工作狀態，基于拉格朗日方程建立對應強耦合、非線性工作的空間雙臂機器人動力學模型，為空間雙臂機器人的設計與研究提供理論基礎。

1 空間雙臂機器人結構及參數

1.1 雙臂機器人虛擬樣機及組成結構

本文結合我國空間站的建造及維護規劃，研究了一種空間雙臂機器人。該機器人由1個工具箱本體和2個DLR型7自由度單臂構成。工具箱用于存儲不同操作任務下的機器人末端工具，同時該工具箱基座通過雙臂的配合能運動到不同的工位進行定位。該機器人能用于空間站的建造及維護，也可代替航天員進行危險的艙外作業，以及配合科學家完成空間科學實驗。空間雙臂機器人的虛擬樣機如圖1所示。

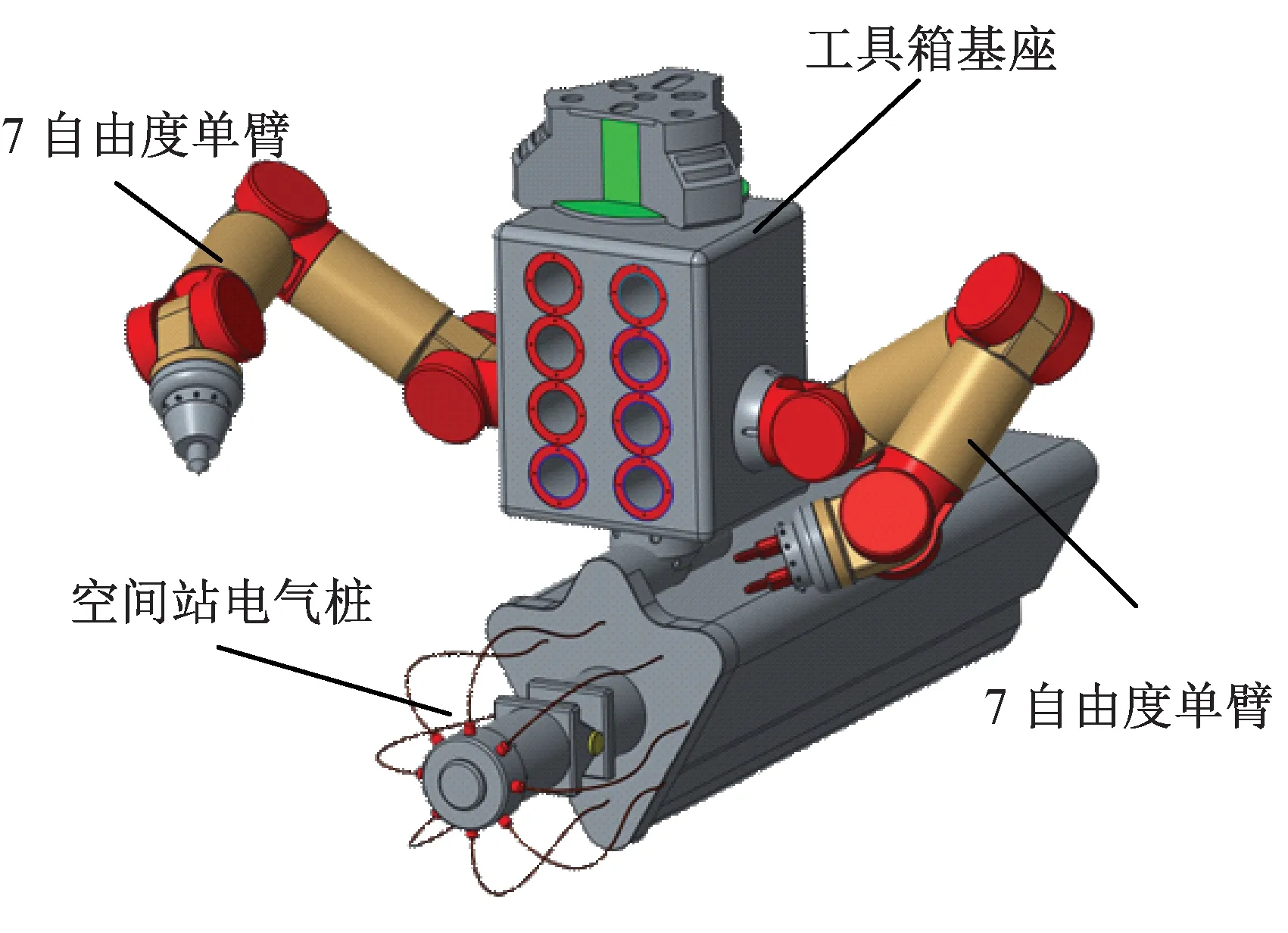
圖1 空間雙臂機器人虛擬樣機Fig.1 Virtual prototyping of dual-arm space robot

1.2 空間雙臂機器人DH參數

為便于分析雙臂機器人的運動學，根據DH坐標系的建立方法，建立空間雙臂機器人的各坐標系如圖2所示[16]。圖2中：∑i為右臂坐標系i；∑i′為左臂坐標系i′；∑b為基坐標系。

由圖2可知：雙臂機器人左右單臂的DH參數相同，參數見表1。表1中：ai為∑i-1與∑i的原點間沿xi軸距離；αi為zi-1軸與zi軸繞xi軸間的夾角；θi為xi-1軸與xi軸繞zi-1軸間的夾角；di為∑i-1與∑i的原點間沿zi-1軸距離。

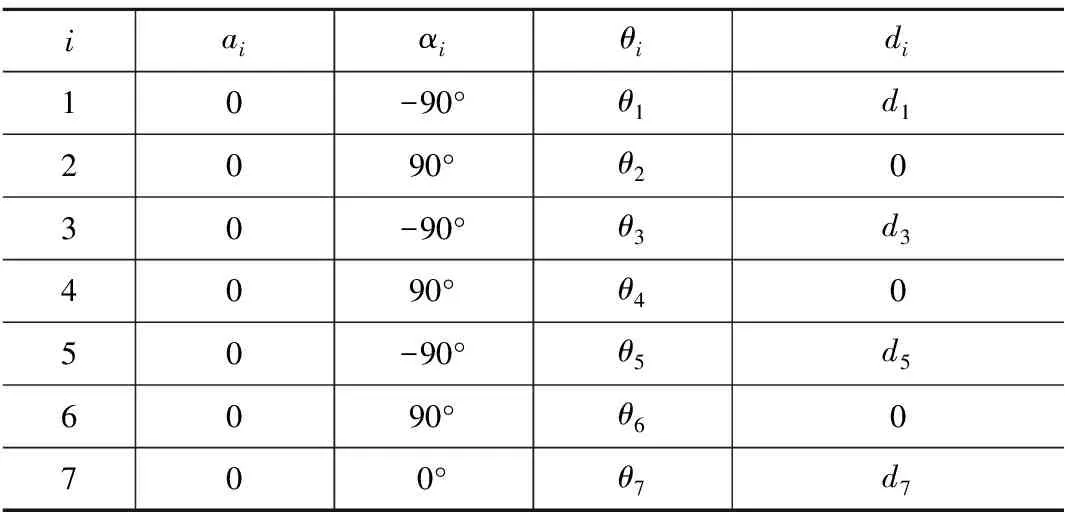
表1 雙臂機器人DH參數

2 空間雙臂機器人運動學

2.1 空間雙臂機器人正運動學

圖2 雙臂機器人DH坐標系Fig.2 DH coordinates of dual-arm space robot

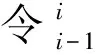
rot(Xi,αi)·tran(ai,0,0)=

(1)

式中：rot(Zi-1,θi)為繞Zi-1軸旋轉θi；tran(0,0,di)為沿Zi-1軸移動距離di；rot(Xi,αi)為繞Xi軸旋轉αi；tran(ai,0,0)為繞Xi軸移動距離ai。由上述定義，可得相鄰兩坐標系齊次變換關系為

[Xi-1Yi-1Zi-11]T

(2)

則0標系至7系的轉換關系可表示為

(3)

[X0Y0Z01]

(4)

2.2 冗余機械臂逆解解法

2.2.1 臂形角定義

在笛卡爾空間中表征一個物體的位姿需要參數6個，而上述機械臂有7個輸入的冗余機械臂。單臂的前三個關節、后三個關節相互正交，如圖3所示，該機械臂單臂可等效為S-R-S構型，分別構成肩關節、肘關節和腕關節。因具冗余特性，對末端同一位姿，機械臂有無窮多組輸入組合能滿足，亦即機械臂存在自運動。

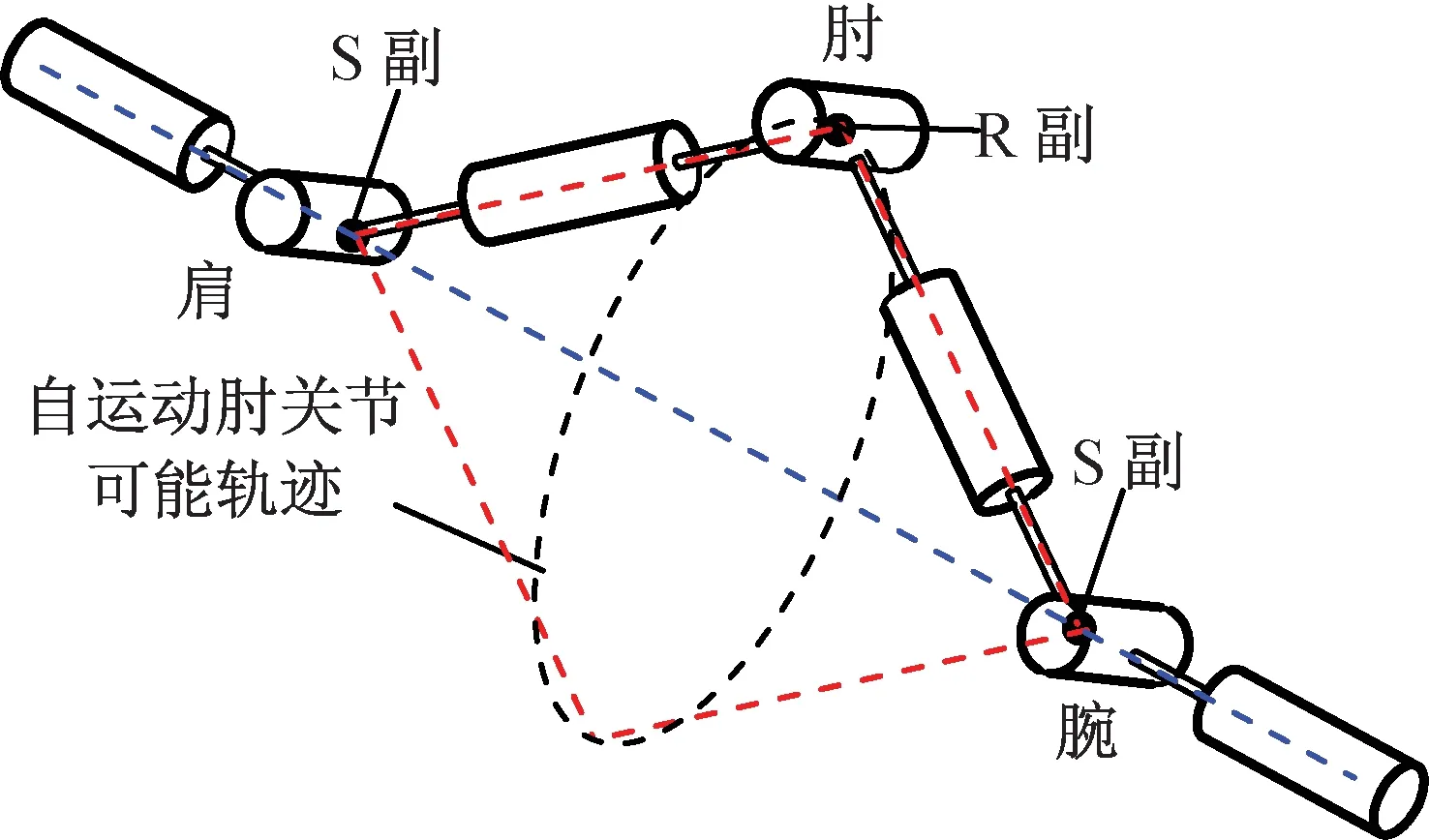
圖3 機械臂等效S-R-S構型Fig.3 Equivalent configuration S-R-S of manipulator

為得到唯一的機械臂逆解，引入臂形角約束[13]。機械臂臂形角定義如圖4所示。圖4中：肩部三關節軸線相交于點S；腕部三關節相交于點W；點E為第四關節坐標系的原點；v為第一關節的軸線矢量。S，E，W三點構成臂型面，v與SW構成參考平面，ψ為臂型面與參考面間的夾角。

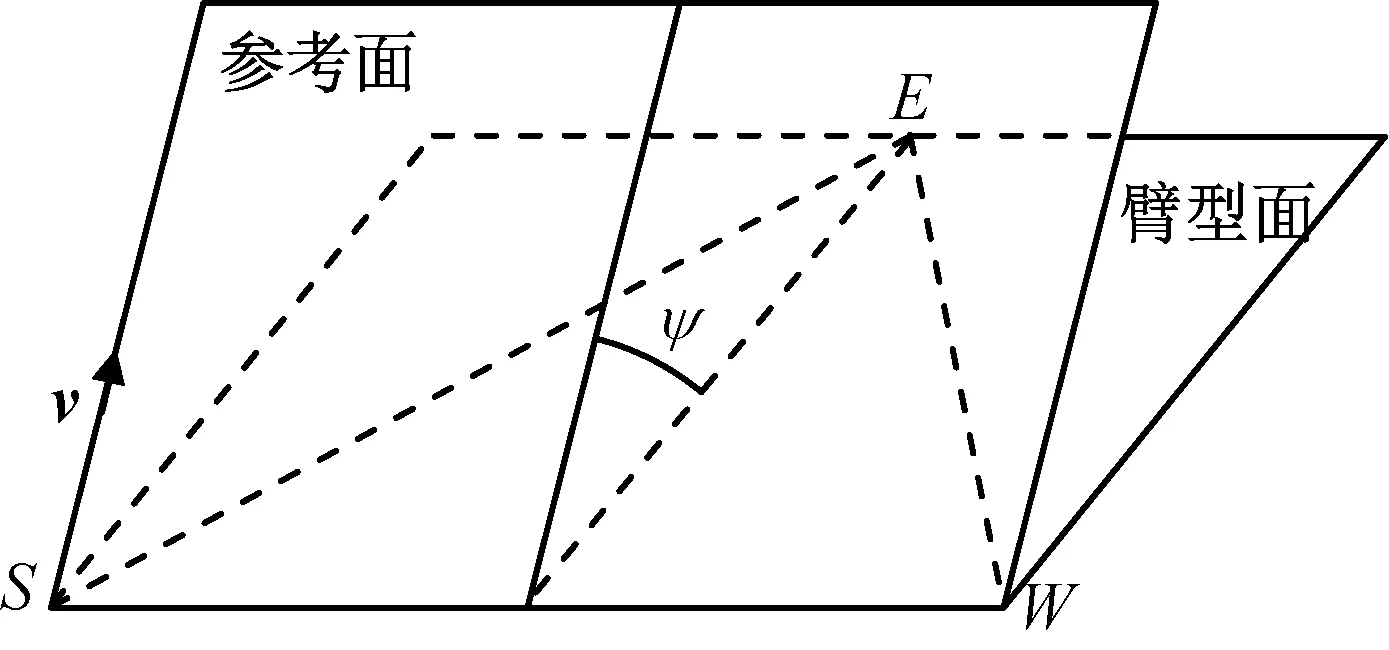
圖4 臂形角定義Fig.4 Definition of arm-angle

2.2.2 肘關節角求解

根據串聯機械臂正運動學，末端工具坐標系位姿在0系中可表示為

(5)

(6)

式中：iRj為i系姿態至j系中姿態的旋轉矩陣；0l0s,3lse,4lew,7lwt為常值向量，且

(7)

(8)

(9)

(10)

此處：d0s為0系原點與點S的距離；dse為點S，E的距離；dew為點E，W的距離；dwt為點W至工具坐標系(即7系)原點的距離。

(11)

則SW在0系中可表示為

0xsw=0x7-0lbs-0R77lwt=0R3(3lse+3R44lew)

(12)

假設機械臂末端的位置與姿態固定時，則SW亦固定，即0xsw固定。因此，對任意固定的末端位姿，此種S-R-S構型的冗余機械臂的自運動不改變腕關節交點W的位置，腕關節的姿態在基坐標系中的表示則取決于繞SW軸的旋轉角度，即腕部的姿態取決于臂形角ψ。繞SW軸的旋轉可表示為按任意軸旋轉變換矩陣

0Rψ=I3+ sinψ[(0usw)×]+

(1-cosψ)[(0usw)×]2

(13)

式中：I3為三階單位陣；0usw為與0xsw對應的單位向量；符號“×”表示反對稱陣。則可得

(14)

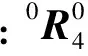
由圖3可知：當末端的位姿固定時，肘部的關節角亦是固定的。此結論可通過計算式(12)的歐式范數驗證，即

(15)

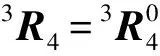
(16)

(17)

將式(16)代入式(5)、(6)，用臂形角表述的運動學方程可寫成

(18)

(19)

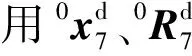
(20)

式中：

(21)

2.2.3 肩關節及腕關節角求解

由于肩關節角依賴于臂形角，先計算出臂形角為零時的參考關節角。如上所述，參考關節角可由固定關節三的關節角為0求解，且參考關節角需滿足

(22)

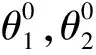
(23)

當臂形角為0時，可得轉移矩陣

(24)

解得

(25)

得到臂形角為0時的第二個關節角

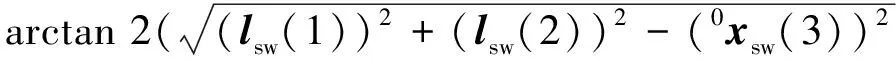
0xsw(3))

(26)

第一個關節角

(27)

(28)

則有

(29)

將式(13)代入式(17)，可得

(30)

式中：

(31)

由于已知旋轉矩陣

0R3=

(32)

式中：

根據式(30)、(32)對應元素相等，可得

(33)

(34)

(35)

式中：aSij,bSij,cSij分別為AS，BS，CS中的(i，j)元素。

同理，將式(13)代入式(19)，可得

(36)

式中：

(37)

由于已知旋轉矩陣

(38)

式中：

根據式(36)、(38)對應元素相等，可得

(39)

(40)

(41)

式(20)、(33)～(35)、(39)～(41)給出了冗余機械臂的求解計算公式。當給定空間雙臂機器人機械臂末端的位姿時，便能求解得到各關節需到達的關節角。

3 空間雙臂機器人動力學

3.1 動力學建模基礎

關于動力學模型的建立方法有拉格朗日方程、牛頓歐拉法、凱恩方程等[14]。拉格朗日法從能量的角度出發，通過對廣義坐標求導得到系統的廣義力；牛頓歐拉法通過分析每根桿件的受力狀況建立迭代形式的動力學方程，易于計算機實現。雙臂機器人在執行任務操作時固聯于空間站上，因雙臂機器人的質量相對空間站可忽略不計，故忽略機器人與空間站的耦合作用，則文獻[15]的角動量守恒方法不適于本文空間雙臂機器人的建模。機器人單臂為串聯結構，采用拉格朗日方程更易于重新建立空間雙臂機器人的動力學模型。

拉格朗日方程為

(42)

式中：Ek，Ep，qi，Fi分別為系統的動能、勢能、廣義坐標和廣義力。

機器人所處的環境失重，Ep項為0，拉格朗日方程式(42)可改寫為

(43)

由式(43)可知：對雙臂機器人的動力學分析只需求出整機系統的動能，再對廣義坐標求導就可得系統所受的廣義力。

求解中，建立坐標系并取廣義坐標qr(i),ql(j)，其中1≤i≤n,1≤j≤m。令qr(i)為右臂第i關節的關節角度，ql(j)為左臂第j關節的關節角度；ωbase,ωtar分別為基座和目標操作物的角速度；mr(i)為右臂第i桿的質量，ml(j)為左臂第j桿的質量；mbase,mtar分別為基座和目標操作物的質量；Ir(i)為右臂第i關節的慣性張量，Il(j)為左臂第j關節的慣性張量；Ibase,Itar分別為基座和目標操作物的慣性張量。取左、右臂桿件質心的笛卡爾坐標分別為(xr(i),yr(i),zr(i))，(xl(i),yl(i),zl(i))；取基座和目標操作物質心的笛卡爾坐標分別為(xbase,ybase,zbase)，(xtar,ytar,ztar)。

空間雙臂機器人系統的總動能為左臂、右臂、基座，以及目標操作物的動能之和，即

(44)

式中：η1，η2為二元判定參數，取值為0或1。此處：右臂、左臂、基座和目標操作物的動能分別為

(45)

(46)

Ibase(ωbase)2]

(47)

Itar(ωtar)2]

(48)

當ηi(i=1，2)取0時，系統不存在對應動能計算項，此時該物體靜止；當ηi取1時，系統存在對應動能計算項，此時該物體運動。

3.2 空間雙臂機器人動力學模型

空間雙臂機器人在執行任務過程中涉及雙臂協同關系的轉換和本體位型的改變。由式(44)，η1對應操作物的狀態，η2對應機器人本體的狀態。當ηi(i=1，2)取0時，該物體靜止；當ηi取1時，該物體運動。根據二元判定參數的取值組合，將機器人位型的轉換歸納為4種工況：當η1=0，η2=0時，機器人本體固定，雙臂運動；當η1=1，η2=0時，雙臂均抓緊扶手，機器人本體運動；當η1=0，η2=1時，對應雙臂均抓緊扶手、機器人本體運動，以及單臂抓住扶手、機器人本體和另外一只臂運動兩種工況。基于式(43)，建立4種工況對應的動力學模型。

3.2.1 工況1——機器人本體固定，雙臂運動

該工況發生在從初始狀態到協同操作狀態的轉換過程中，此時左右臂同時運動，但不執行末端操作，如圖5(a)所示。圖5(a)中：空間雙臂機器人本體固聯于空間站電氣樁上，雙臂運動為插拔電氣元件做準備。

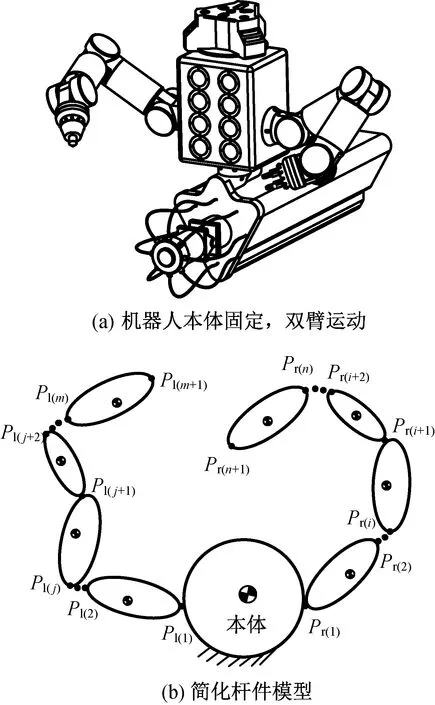
圖5 工況1Fig.5 Case 1

工況1的機器人簡化桿件模型如圖5(b)所示，可分別求出指定運動情況下的左右臂的關節力矩。圖5中：Pl(j),Pr(i)分別為左臂第j關節、右臂第i關節的坐標。該工況的系統動能可表示為

(49)

3.2.2 工況2——機器人本體固定，雙臂協同操作

該工況發生在機器人固定在一個固定工位，雙臂共同完成協同任務，如共同拆裝航天器插件、擰螺絲等時。機器人本體固定在空間站電氣樁上，雙臂協同操作進行航天器插件的拆裝維護工作，如圖6所示。

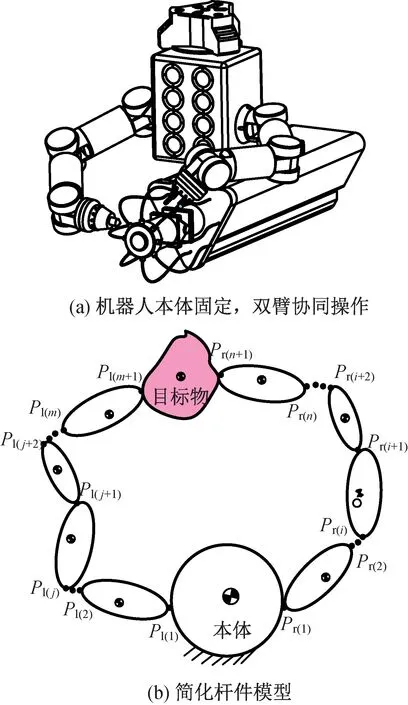
圖6 工況2Fig.6 Case 2

在圖6(b)桿件簡化模型中目標操作物也處于運動狀態，需在計算系統動能時加入目標操作物的動能，目標操作物的位姿則可由左右臂的協同關系解得。該工況的系統動能可表示為

(50)

3.2.3 工況3——雙臂均抓緊扶手，機器人本體運動

該工況發生在機器人在空間站上自主從一個工位轉移到另一個工位時，此時需調整本體的位置。在此過程中左右臂末端桿件固定，本體發生運動，如圖7所示。

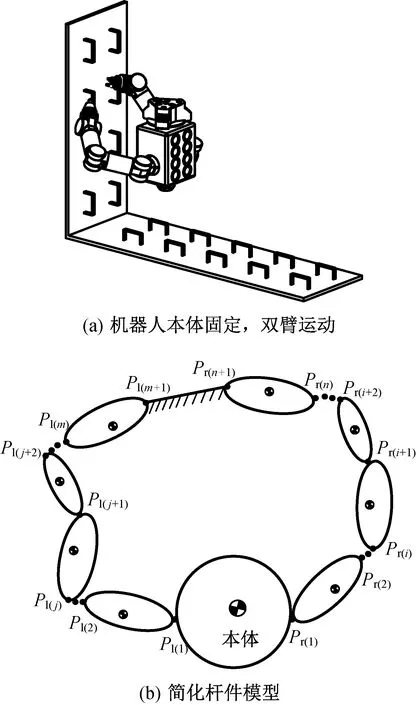
圖7 工況3Fig.7 Case 3

在圖7(b)桿件的簡化模型中機器人本體運動，左右臂末端固定。計算系統動能時左右臂末端桿件動能為0。機器人本體位姿則可由左右臂的協同關系來解得。該工況的系統動能可表示為

(51)

3.2.4 工況4——單臂抓住扶手，機器人本體和另外一只臂運動

該工況發生在機器人在空間站上工位轉移過程中。機器人一只臂抓住空間站扶手，另一只臂準備抓住下一工位的扶手，如圖8所示。

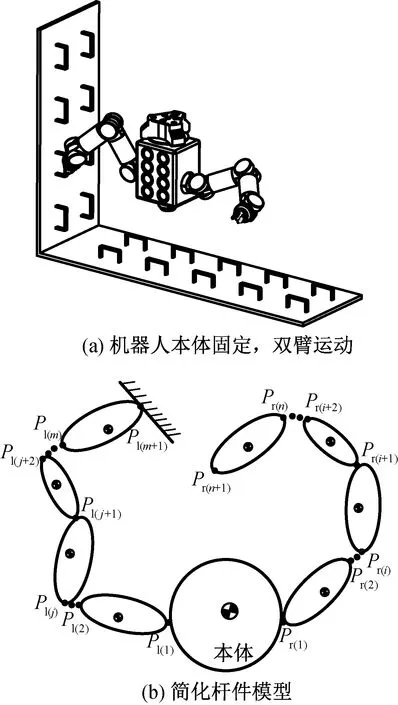
圖8 工況4Fig.8 Case 4

在如圖8(b)所示桿件簡化模型中，左臂的末端固定，其余桿件，包括基座均處于動態，因此可用串聯臂的解法求出各桿件位置。該工況的系統動能可表示為

(52)

將式(49)～(52)代入式(44)，可得簡化形式的動力學方程為

τ

(53)

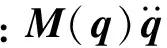
4 結束語

本文對失重狀態下的空間雙臂機器人的運動學及動力學建模進行了研究。由分析實際工程應用中的雙臂機器人的結構參數，用臂形角的解法，給出了求解效率更高的空間雙臂機器人的運動學逆解解析方法。分析了空間雙臂機器人在執行任務中的狀態，引入二元判定參數，歸納得到了雙臂獨立運動、雙臂協同操作、閉鏈本體漂浮、開鏈本體漂浮4種強耦合、非線性工作狀態下的動力學模型。通過對空間雙臂機器人變構型工作狀態下的運動學及動力學分析，為后續空間雙臂機器人的研制提供理論基礎。后續將構造虛擬工況，對空間雙臂機器人的運動學及動力學特性做進一步的研究與驗證。

[1] 梁斌, 杜曉東, 李成, 等. 空間機器人非合作航天器在軌服務研究進展[J]. 機器人, 2012, 34(2): 242-256.

[2] FLORES-ABAD A, MA O, PHAM K， et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68: 1-26.

[3] REMBALA R, OWER C. Robotic assembly and maintenance of future space stations based on the ISS mission operations experience[J]. Acta Astronautica, 2009, 65(7-8): 912-920.

[4] NASA. Dextre, Space Electrician: Canadian robot repairs components on the Space Station[EB/OL]. [2016 -12 -29]. https://www.nasa.gov/mission_pages/station/structure/space_electrician.html.

[5] DIFTLER M A, MEHLING J S, ABDALLAH M E, et al. Robonaut 2—the first humanoid robot in space[C]// IEEE International Conference on Robotics and Automation. Shanghai, IEEE, 2011: 2178-2183.

[6] MACIEJEWSKI A A. Obstacle avoidance for kinematically redundant manipulators[J]. International Journal of Robotics Research, 1985, 4(3): 109-117.

[7] TAN F C, DUBEY R V. A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators[J]. IEEE Transactions on Robotics & Automation, 1993, 11(2): 286-292.

[8] CHIAVERINI S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators[J]. IEEE Transactions on Robotics and Automation, 1997, 13(3): 398-410.

[9] NEDUNGADI A, KAZEROUINIAN K. A local solution with global characteristics for the joint torque optimization of a redundant manipulator[J]. Journal of Robotic Systems, 1989, 6(5): 631-654.

[10] YOSHIKAWA T. Manipulability of robotic mechanisms[J]. The International Journal of Robotics Research, 1985, 4(2): 3-9.

[11] NAKAMURA Y, HANAFUSA H. Inverse kinematic solutions with singularity robustness for robot manipulator control[J]. Journal of Dynamic Systems Measurement & Control, 1986, 108(3): 163-171.

[12] LUCA A D, ORIOLO G. The reduced gradient method for solving redundancy in robot arms[J]. Robotersysteme, 1991, 7: 117-122.

[13] SHIMIZU M, KAKUYA H, YOON W K, et al. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution[J]. IEEE Transactions on Robotics, 2008, 24(5): 1131-1142.

[14] 張策. 機械動力學[M]. 2版. 北京: 高等教育出版社, 2008.

[15] 顏世佐. 空間機器人協調控制與地面實驗研究[D]. 哈爾濱: 哈爾濱工業大學, 2009.

[16] SICILIANO B. Robotics: modelling planning and control[M]. London: Springer, 2009.

Kinematics and Dynamics Modeling for Dual-Arm Space Robot

WU Chang-zheng1, LIU Dian-fu2, YUE Yi1, 3, WEI Bao-chen1

(1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University,Shanghai 200240, China; 2. Aerospace System Engineering Shanghai, Shanghai 201109, China; 3. Shanghai Aerospace Equipments Manufacturer, Shanghai 200245, China)

To establish the kinematics and dynamics model of dual-arm space robot, a study was made to analysis the characters of the robot in non-gravity environment and modeling in this paper. The formulation for forward kinematics of the right and left arm was given out in terms of the robot’s DH parameters. A more efficiency method to solve the inverse kinematics for redundant was derived based on the arm-angle approach. The 2 coefficients of determination parameters were introduced to describe the working condition for space robot. The working condition was analyzed for dual-arm space robot and 4 different kinds of dynamics equations were given based on the Lagrange’s equations, which were the two arms moved independently, the two arms cooperated, the base floating with closed chain and the base floating with open chain. The modeling of kinematics and dynamics laid the foundation for the design and analysis for dual-arm space robot.

dual-arm space robot; redundant; analytical; inverse kinematics; dynamics; non-gravity; modeling; coefficient of determination

1006-1630(2017)03-0080-08

2017-01-12；

2017-03-06

國家自然科學基金資助(61473187)；教育部青年教師基金資助(20130073120045)；航天先進技術聯合研究中心技術創新項目資助(USCAST2015-36)

吳長征(1992—)，男，碩士生，主要從事機器人運動規劃研究。

TP242.3

A

10.19328/j.cnki.1006-1630.2017.03.011