基于線性損傷理論的筒形缸紅套環蠕變損傷累積研究

趙仕志，劉東旗，陳鐵寧，張明

（東方汽輪機有限公司，四川德陽，618000）

基于線性損傷理論的筒形缸紅套環蠕變損傷累積研究

趙仕志，劉東旗，陳鐵寧，張明

（東方汽輪機有限公司，四川德陽，618000）

紅套環筒形缸在大功率汽輪機中使用越來越廣泛，隨著機組參數的升高，紅套環不可避免地處于蠕變狀態。合理確定紅套環的初始緊力，檢修周期以及保證運行的安全可靠性都必須考慮蠕變效應，但是針對紅套環的蠕變損傷累積研究還比較少見。文章基于線性損傷理論，結合拉松-米勒參數法（簡稱L-M法）建立了紅套環蠕變損傷計算的一般形式，并研究了初始緊力和大修周期對損傷累積的影響。對于理解紅套環服役期內的性能退化過程和指導工程設計有顯著意義。

汽輪機，紅套環，蠕變損傷，損傷力學

0 引言

發展超超臨界汽輪機機組，能大幅度提高單機的發電效率，以滿足經濟發展、環境保護及能源節約的多重需求。但隨著進汽參數的不斷提高，汽缸的幾何尺寸相應增加，這樣在機組啟動、停機和變工況時，導致汽缸法蘭內外壁溫差過大，從而產生很大的熱應力，直接影響機組的安全穩定運行[1]。紅套環筒形缸結構是克服這些困難的一種可行方案，近年來得以廣泛使用。

對于高溫區工作的紅套環來說，蠕變是不可避免的。由于蠕變效應，紅套環材料中的損傷不斷累積，當損傷累積到一定程度就可能導致紅套環破壞，所以紅套環的蠕變壽命是影響機組安全性的重要指標。從另一方面來說，紅套環通常是加工精度要求極高的高溫合金大鍛件制品，其母材，鍛冶和機加成本都非常高昂。如不能準確地預測紅套環剩余壽命而提前報廢將使汽輪機的運行和維護成本顯著增加。因此，高溫紅套環的損傷累積研究和壽命評估有重要的工程意義。

目前國內外已有大量關于汽輪機部件蠕變壽命損傷的研究和報道，但是這些研究多數集中在葉片和轉子[2-6]領域，也有部分文獻將研究對象選定為螺栓或汽缸[5,7-9]，但是對筒形缸紅套環的蠕變損傷研究還比較少見。

本文基于線性損傷理論建立了紅套環蠕變損傷計算的一般形式，并結合拉松－米勒蠕變模型，初步建立了紅套環蠕變損傷累積和允許大修次數的計算方法。

1 理論分析

1.1 線性損傷理論

與轉子部件主要載荷是恒定的離心力不同，對于紅套環，其主要的載荷是由裝配過盈量引起的裝配應力。由于蠕變效應，紅套環的應力狀態在持續變化。因此在轉子部件設計中常用的拉松－米勒法不能直接用于紅套環的蠕變損傷和蠕變壽命分析。研究這類應力持續變化部件蠕變損傷的常用方法是壽命－時間分數法，也就是線性損傷累積法則。該方法雖然古老，且精度稍差，但是由于形式簡單，計算方便，目前仍然是應用最廣泛的損傷累積法則，并且是ASME列入鍋爐和壓力容器設計規范的唯一方法[10-11]。因此本文的研究采用該方法。

線性損傷理論認為各變應力和變應變所引起的損傷可分別計算并線性疊加。其基本公式[10]是式（1）:

1.2 第一個大修周期內的損傷累積

對于本文所研究的紅套環。可以假設在溫度T和應力σ下紅套環的蠕變斷裂時間lif有如下的形式，見式（2）:

首先來分析第一個檢修周期t1內的情況。在紅套環服役期內某時間點的時間微元dt內，因為時間很短，可認為溫度T和應力σ均不變。根據式（1），在該時間微元dt內紅套環的損傷可表示為式（3）:

那么，紅套環在第一個檢修周期t1內，其累積損傷為式（4）:

將式（2）帶入式（4），紅套環的累積損傷可表示為式（5）:

在全壽命周期內溫度T和應力σ均是時間t的函數。要確定此兩函數并不難[13]。特別是由于有限元技術的廣泛應用，當材料和工況確定后，只需要按照熱邊界條件和材料的蠕變模型就可以很準確地計算出溫度T和應力σ的時間歷程曲線。詳細的計算過程不是本文研究重點，不再贅述。最一般的情況，可以假設溫度T和應力σ為如下形式的已知函數，見式（6）、式（7）:

將式（6），（7）帶入式（5）可得最一般的情況下，第一個檢修周期t1內的總損傷為式（8）:

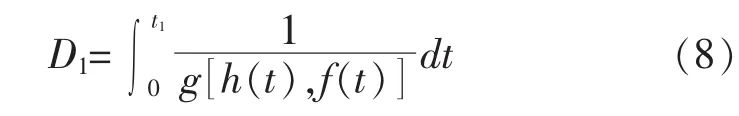
顯然，式（8）其實是一個時間t的單變量函數。由于h（t），f（t）為已知函數，只要確定函數g（t）的形式就可以確定在第一個大修周期內紅套環所累積的損傷。這就是紅套環線性蠕變損傷累積模型的一般形式。

g（t）的確定需要知道材料的蠕變模型。由于在時間微元dt內溫度和應力均可以認為是不變的，因此可以使用拉松-米勒參數進行分析和計算。

對于金屬材料LMP參數方程通常可表示為式（9）:

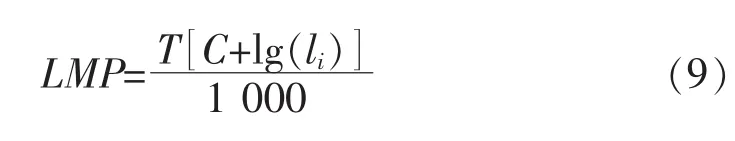
其中:

T:溫度，K；

C:以材料相關的常數，通常取值在20～25；

li:載荷保持時間。

當以材料持久強度性能數據帶入式（9）時有li= lif，式（9）變為式（10）:

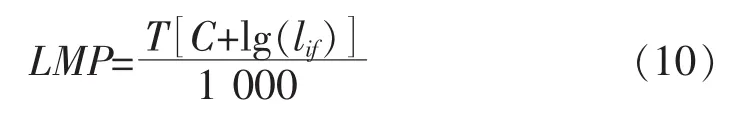
另一方面，對于確定的材料，應力和LMP參數間成確定的函數關系。對于金屬材料，通常LMP和σ成二次函數關系。一般的可以假設[14]為式（11）:

對式（11）求解LMP可得式（12）:

其中A，B和E是與材料相關的常數。因此，只需要知道材料3個以上不同試驗工況的持久性能試驗數據就可以確定這3個常數，從而確定式（11）和（12）。因此式（12）也可視為已知的。于是，將式（10）帶入式（12）并經代數運算有式（13）:

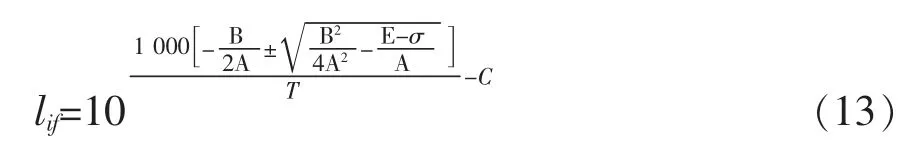
式（13）就是g（t）函數的形式。將式（6），式（7）帶入式（13），然后再將式（13）帶入式（4）可得第一個大修周期內紅套環的累積損傷為式（14）:

至此，只要根據有限元計算結果確定h（t），f（t）就可以通過式（14）確定一個大修周期內紅套環的壽命損傷。這就是基于拉松-米勒模型的紅套環線性蠕變損傷累積模型的詳細形式。式（14）中“±”的確定與試驗數據的擬合函數有關。根據LMP參數的意義可以確定，當A〉0時取“-”，反之取“+”。

1.3 最大允許大修次數的確定

由于高溫蠕變，紅套環緊力會持續下降，因此在一段時間后就需要通過調整手段增加紅套環的緊力以保證內缸的密封性。增加墊片后紅套環緊力增加，并再次進入新一輪的損傷累積過程。為簡化模型，假設大修后緊力完全恢復到首次初裝緊力，并且材料性質與第一個運行周期內相同。那么在大修后新的運行周期內紅套環將與第一個大修周期內有相同的h（t），f（t）和g（t）函數，那么新運行周期內的損傷累積也與第一個運行周期相同。以此類推，經過n個運行周期后總的累積損傷（含第一個周期）為式（15）:

當許用損傷為［D］時，保證紅套環安全使用的條件是式（16）:

至此，只要根據工程經驗確定紅套環的許用蠕變損傷［D］后就可確定紅套環允許的最多大修次數為式（17）:

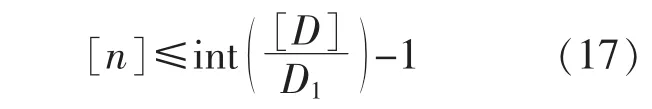
注意，式（17）計算的是允許大修的次數，不含第一次初裝在內。int（）表示取整。

2 設計實例

某汽輪機高壓內缸采用紅套環筒形缸結構。最危險紅套環工作溫度530℃。設計首次大修周期為10萬小時。內缸外徑1 670 mm，推薦的初始過盈量為:0.835 mm。詳細設計階段發現，0.835 mm的過盈量下長期運行后內缸中分面汽密性不夠理想。因此考慮增加過盈量到1.106 5 mm或1.25 mm。常規的強度校核顯示各方案下紅套環強度均滿足要求，汽密性校核顯示長期運行后不同過盈量下汽缸的汽密性差異并不顯著。現在比較分析3種過盈量下紅套環的蠕變損傷累積過程以確定最合理的設計方案。

2.1 第一個大修周期內的損傷累積

該內缸上最危險的紅套環工作溫度約530℃。保守的假設紅套環始終工作在該溫度下，即h（t）＝530＋273.15。式（14）可以進一步簡化為僅是f（t）的復合函數。

通過有限元方法可求得不同的過盈量δ下紅套環的應力時間曲線如圖1所示。從圖1可以看出，不同的過盈量下紅套環的初始應力差異顯著，過盈量1.25 mm時紅套環初始應力比過盈量0.835 mm時高約24%。但是經過4萬小時松弛后的應力就幾乎無差別了。這就解釋了不同過盈量，長期運行后密封性基本相當的原因。

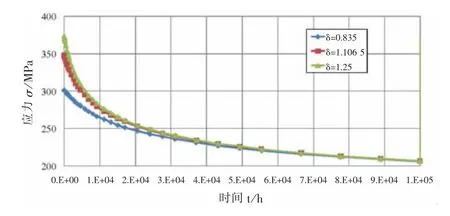
圖1 不同過盈量下紅套環的應力松弛曲線

擬合圖1所示的應力－時間曲線得到f（t）并代入式（14）可求得不同初始過盈量下第一個大修周期（10萬小時）內紅套環的損傷累積過程。計算結果如圖2所示。表1是不同過盈量的詳細比較。從圖2和表1容易看出不同過盈量下10萬小時后紅套環的累積損傷差異巨大。紅套環預緊量從0.835 mm增加到1.106 5 mm后紅套環的初始應力升高了約16%，但是10萬小時后的累積蠕變損傷增加了50%。過盈量增加到1.25 mm后，初始應力升高了約24%，但是10萬小時后累積蠕變損傷量增加了88%。這表明累積損傷與初始應力之間不是線性關系，初始緊力相對小的增加可能導致累積損傷發生根本變化。

圖2 不同過盈量下紅套環的損傷累積曲線

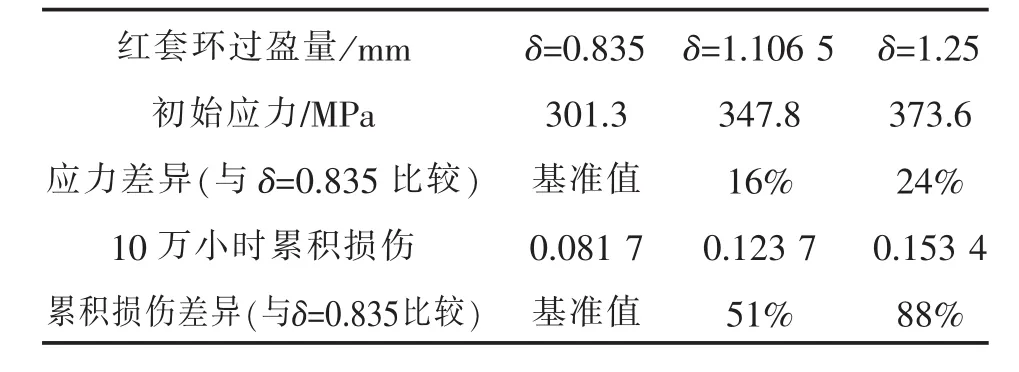
表1 不同初始過盈量下10萬小時后紅套環的累積損傷

從圖2中還可以看出，實際上4萬小時后不同初始過盈量下紅套環的損傷累積速率基本一致。導致累積損傷顯著差異的主要是初始2萬小時內的累積損傷。導致該現象的原因與材料的蠕變特性相關。如圖3所示為紅套環材料530℃時的壽命-應力曲線。從圖中可知，材料在373.6 MPa（δ=1.25 mm時的初始應力）應力下的蠕變壽命僅為301.3 MPa（δ=0.835 mm時的初始應力）下的1/7左右。也就是說，在初始階段，過盈量δ=1.25 mm時的損傷累積速度約為過盈量δ=0.835 mm時的7倍。因此在初始2萬小時內不同初始過盈量下紅套環應力的差異導致了損傷累積速度的顯著差異，從而顯著影響全服役期內的損傷累積。

圖3 紅套環材料不同應力下的壽命-應力曲線（530℃）

由以上分析可見，初始應力較小的差異會導致紅套環累積損傷發生顯著變化。因此，設計紅套環時應避免不必要的過盈量增加。

2.2 紅套環的最大允許大修次數

對于上節分析的紅套環，其大修周期為10萬小時。如前假設，大修后緊力完全恢復到初始緊力，且材料性質保持不變。那么在每個大修周期內紅套環的應力和損傷累積曲線相同。作為理論分析，理想的假設［D］=1。按式（17）和表1可確定各方案下紅套環允許的最大大修次數如表2所示。

表2 不同方案下紅套環的最大允許大修次數

從表中可知，上述紅套環過盈量δ＝0.835 mm時，紅套環允許大修11次。當過盈量δ＝1.106 5 mm時，紅套環允許大修7次。而當過盈量δ＝1.25 mm時紅套環允許大修5次。紅套環的總使用壽命顯著縮短了。單從數據來看，無論哪種過盈量下紅套環都具有足夠的壽命。但是要注意的是，上述許用損傷按1假設是非常冒進的，同時上述分析沒有考慮服役期內疲勞損傷的影響。

2.3 大修周期對蠕變損傷累積的影響

如前所述，在每個運行周期的初始階段，由于松弛不充分，紅套環應力較高。高應力會導致損傷累積速度顯著增加。因此不必要的縮短大修周期會導致紅套環持續處于高應力狀態，其損傷的累積速度也將顯著增加。

對于本例，考慮過盈量δ＝1.106 5 mm的情況，如圖4所示為紅套環大修周期分別為5萬小時和10萬小時時的應力－時間曲線和損傷累積曲線比較。理想的考慮[D]=1，各大修周期下紅套環的總使用壽命如圖5所示。從圖中可知，大修周期為10萬小時時紅套環可安全使用80萬小時，當大修周期為5萬小時時紅套環的總使用約45萬小時，大修周期2萬小時時，總使用壽命約24萬小時。理論上當檢修周期無限短時，紅套環應力持續為初裝應力347.8 MPa，此時紅套環壽命約5.2萬小時。

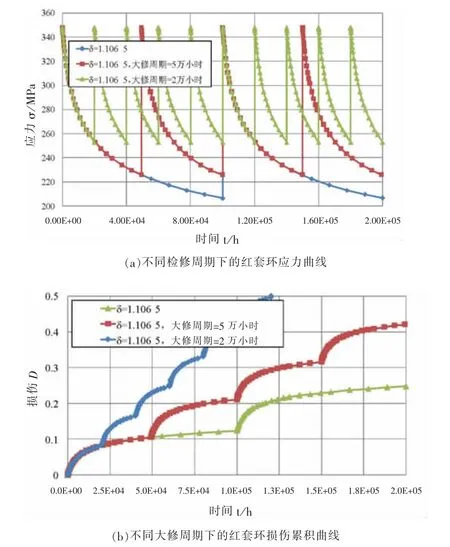
圖4 不同大修周期下紅套環的應力和損傷累積曲線

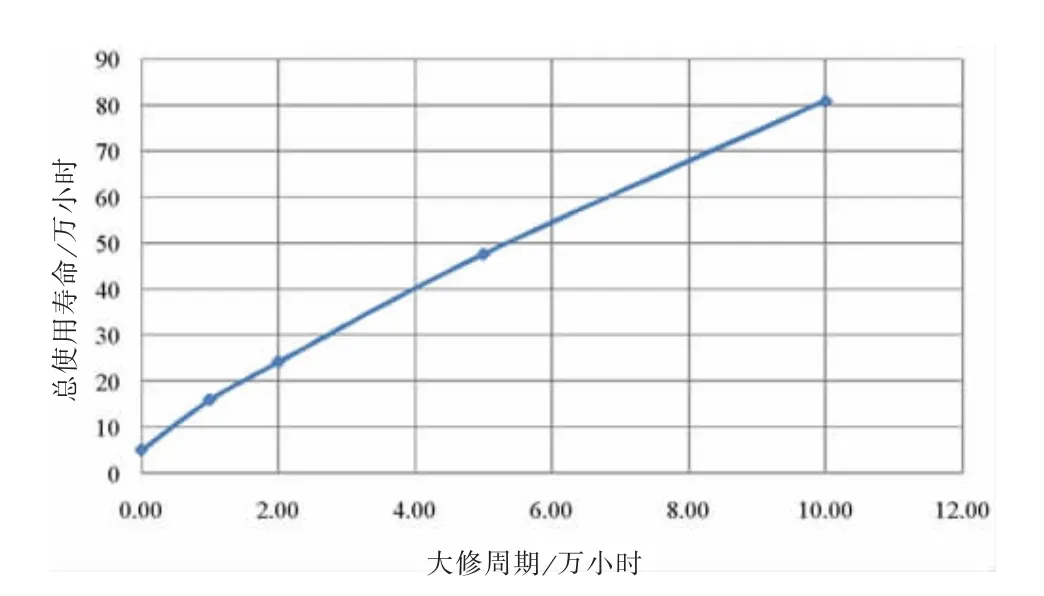
圖5 使用壽命－大修周期關系曲線

本計算實例的分析表明，過高的初始緊力會導致紅套環的損傷累積速率顯著增加，同時還會導致紅套環允許大修的次數顯著下降。綜合考慮汽密性和損傷累積效果后認為過盈量δ＝1.106 5 mm的方案更優。

3 總結

本文基于線性損傷理論建立了紅套環在服役期內蠕變損傷模型的一般形式，以及基于拉松－米勒蠕變模型時的詳細模型，初步建立了紅套環允許大修次數的計算方法。對于理解紅套環服役期內的性能退化過程和指導工程設計有顯著意義。

基于本文創建損傷模型的理論和算例分析表明:

（1）由于蠕變效應，即使增加紅套環的初始緊力，紅套環的密封緊力也會在較短的時間內下降到和沒有刻意增加初始緊力時相近的狀態，因此增加紅套環的初始緊力并不能長期有效地提高汽缸的密封性；

（2）較小的初始緊力增加可能導致損傷累積速度顯著加快，更進一步的，這種影響將顯著減少紅套環允許大修的次數，從而顯著影響紅套環的使用壽命和運行維護成本；

（3）不必要的縮短大修周期會導致紅套環始終處于較高的應力狀態。這將導致紅套環持續處于損傷快速累積的狀態。從而大大影響紅套環的使用壽命。

作為方法研究，本文的分析沒有考慮多軸效應的影響。實際紅套環處于徑向切向應力共同作用的多軸應力狀態下，多軸效應必須考慮。另一方面，雖然本文算例中紅套環的計算壽命很充足，但是本文中理想的假設許用損傷[D]=1是非常冒進的。最后，本文的分析僅考慮了蠕變損傷累積，實際紅套環還要承受疲勞載荷。蠕變和疲勞間有耦合效應這些問題將在以后的工作中進一步研究。

[1]劉東旗,黃果,張曉東,等.大功率汽輪機筒形內缸的強度和汽密性分析[J].東方電氣評論,2015,29(2)：24-28.

[2]史進淵,孫慶,楊宇,等.大型汽輪機部件蠕變壽命的設計和評估[J].中國電機工程學報,2002,22(3)：103-107.

[3]王立濱,荊建平,孫毅,等.損傷力學方法在汽輪機高溫蠕變損傷分析中的應用[J].汽輪機技術,2002,44(2)：88-90.

[4]劉華鋒,王煒哲,蔣浦寧,等.超超臨界汽輪機轉子蠕變對低周疲勞應變的影響[J].動力工程學報,2010,30(9)：715-718.

[5]毛劍峰,王煒哲,張軍輝.超超臨界汽缸高溫強度及多軸蠕變分析[J].力學季刊,2013,34(3)：437-443.

[6]吳穹,王煒哲,張軍輝,等.超超臨界汽輪機中壓轉子高溫蠕變強度分析[J].動力工程學報,2015,35(1)：25-29.

[7]徐鴻,鄭善合,Karl M.超超臨界汽輪機汽缸緊固螺栓高溫蠕變斷裂研究[J].中國電機工程學報,2007,27(29)：80-83.

[8]王爭艷,李德華.超超臨界汽輪機主汽門閥殼高溫蠕變強度分析[J].熱力透平,2010,39(4)：274-277.

[9]毛劍峰,王煒哲,張軍輝,等.汽輪機螺栓松弛對汽缸蠕變強度的影響[J].動力工程學報,2013,33(2)：107-111.

[10]航空渦噴、渦扇發動機結構設計準則（研究報告）審定委員會.航空渦噴、渦扇發動機結構設計準則（研究報告）：第三冊：葉片[R].中國航空工業總公司發動機系統工程局,1997.

[11]閆曉軍,聶景旭.渦輪葉片疲勞[M].北京：科學出版社, 2013.

[12]周順深.火電廠高溫部件剩余壽命評估[M].北京：中國電力出版社,2006.

[13]中國動力工程學會.火力發電設備技術手冊：第二卷：汽輪機[M].北京：機械工業出版社,2007.

[14]P Singh M,M Lucas G.Blade Design and Anlysis for Steam Turbines[M].McGraw-Hill,2011.

Cumulative Creep Damage Analysis of Cylinder Shrink Ring Based on Linear Damage Theory

Zhao Shizhi，Liu Dongqi，Chen Tiening，Zhang Ming

（Dongfang Turbine Co.,Ltd.,Deyang Sichuan,618000）

The cylinder with shrink ring has been used more and more.With the increasing of the unit parameters,the shrink ring has to work under creep condition.Because of this,during design the initial interference and the maintenance cycle,ensure the safe and reliability of the turbine,the engineers have to consider the creep effect of material.While,the analysis about the shrink ring creep damage is rarely reported.This paper bases on the linear damage theory and the larson-miller method(short as L-M method) to build the general form of the shrink ring creep damage,and studies the effect of the initial interference and maintenance cycle on the creep damage.The conclusion has signification meaning for both understanding the degradation of the shrink ring and guiding engineering design.

steam turbine,shrink ring,creep damage,damage mechanics

TK262

A

1674-9987（2017）02-0036-06

10.13808/j.cnki.issn1674-9987.2017.02.009

趙仕志（1982-），男，工學碩士，工程師，畢業于西安交通大學固體力學專業，現從事汽輪機，燃氣輪機的結構、強度和振動設計工作。