關于某些P-葉解析函數類的系數估計

敖恩, 李書海, 斯琴其木格

(1.赤峰學院數學與統計學院,內蒙古 赤峰 024000;2.赤峰學院計算機與信息工程學院,內蒙古 赤峰 024000)

關于某些P-葉解析函數類的系數估計

敖恩1, 李書海1, 斯琴其木格2

(1.赤峰學院數學與統計學院,內蒙古 赤峰 024000;2.赤峰學院計算機與信息工程學院,內蒙古 赤峰 024000)

利用擬從屬關系引進了一些新的P-葉解析函數的子類,應用解析函數的基本不等式和分析技巧,討論了相應函數類的系數估計,得到了準確結果,推廣了一些相關結果,并給出了 Hadamard卷積在 Fekete-Szeg¨o問題上的應用.

解析函數;P-葉函數;擬從屬;系數估計;Fekete-Szeg¨o問題;Hadamard卷積

1 引言

單葉函數和多葉函數的系數估計問題一直受到各國數學家高度重視.Fekete-Szeg¨o問題是解析函數系數方面研究的一個重要分支,這類問題實質上是對單葉函數的第二項系數和第三項系數之間關系的一個估計.具體的來說是估計單葉函數類上的系數泛函的上界.在1933年,文獻[1]首先提出了單葉函數類上的系數泛函的精確估計問題,并得到結果.

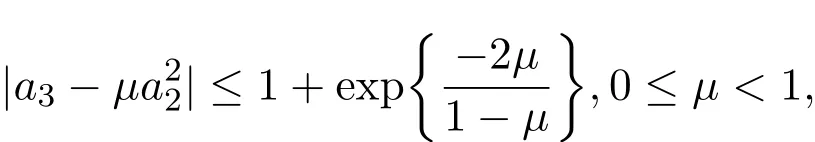
且對任意的μ∈[0,1)等號均成立.由此,許多研究者利用從屬關系引進單葉函數的各種子類,對函數類的 Fekete-Szeg¨o問題進行了研究 (如文獻 [2-6]).在對單葉解析函數的 Fekete-Szeg¨o問題研究基礎上,許多學者對多葉解析函數的Fekete-Szeg¨o問題也進行了研究.最近,在文獻[7-11]中,一些研究者利用比從屬關系具有更廣泛意義的擬從屬關系引進了一些單葉和雙向單葉解析函數子類,并研究了函數類的系數估計和Fekete-Szeg¨o問題.受到上面文獻的啟發,本文利用擬從屬關系引進三類P-葉解析函數,討論了相應函數類的系數估計和Fekete-Szeg¨o問題,得到了準確結果,從而推廣了文獻[7,12]中一些相關結果,并給出了Hadamard卷積在Fekete-Szeg問題上的應用.

2 預備知識

設Ap表示在單位圓盤D={z:|z|<1}內解析,且具有如下形式:

3 系數估計

為了得到本文的主要結果,需要引進下面的引理.

引理 3.1[14]設φ(z)=c0+c1z+c2z2+···在單葉圓盤 D 內解析且

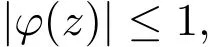
則

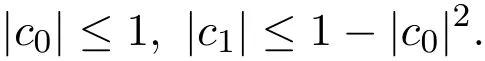
引理 3.2[14]設 ω(z)=ω1z+ω2z2+···在單葉圓盤 D 內解析且|ω(z)|<1,則對任意復數t,有

當函數ω(z)=z2或ω(z)=z時上式等號成立.

引理 3.3[15]設 ω(z)=ω1z+ω2z2+···在單葉圓盤 D 內解析且|ω(z)|<1,則對任意實數t,有

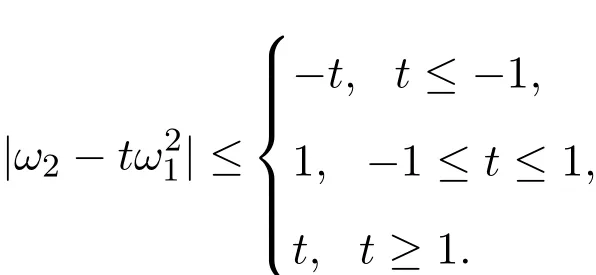
又將函數φ(z),?(z)和ω(z)的冪級數展開式代人(5)式右側,整理可得

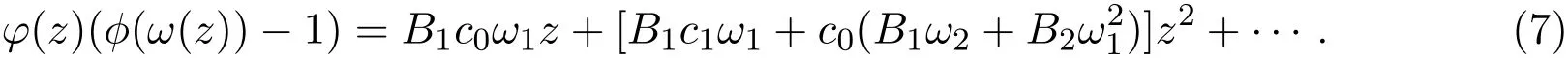
于是將(6)式和(7)式代入到(5)式,比較兩邊同次冪的系數可得

在定理1中,令ω(z)=z,得到如下結論.

推論 3.1如果f(z)∈Ap滿足:

且對任何復數μ,有

當μ≤σ1或者μ≥σ2時,分別有t≤?1和t≥1.于是應用引理3.3,可得(10)式中第一個和最后一個不等式;又當σ1≤μ≤σ2時,有|t|≤1.由引理3.3,可知(10)式中第二個不等式也成立.

當μ<σ1或者μ>σ2時,對應的極值函數f(z)滿足:

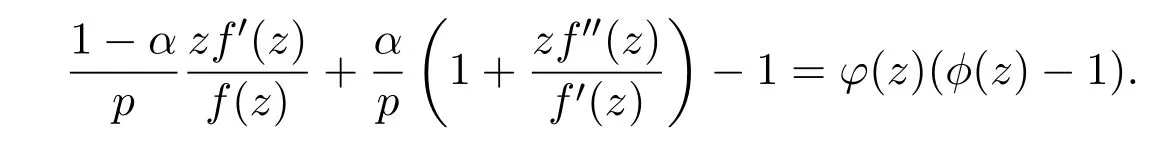
當σ1<μ<σ2時,對應的極值函數f(z)滿足:

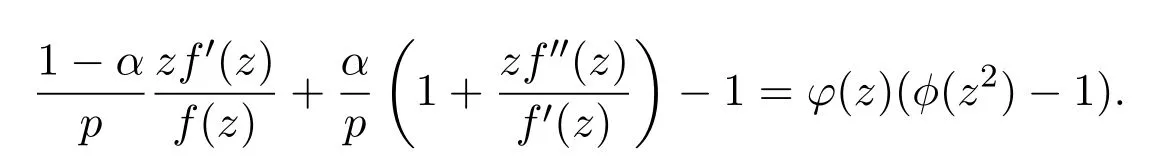
當μ=σ1或者μ=σ2時,對應的極值函數f(z)分別滿足:

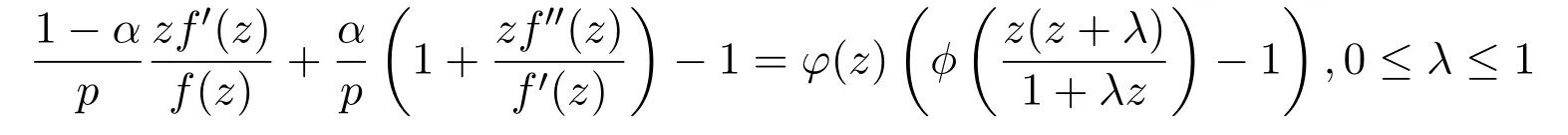
和

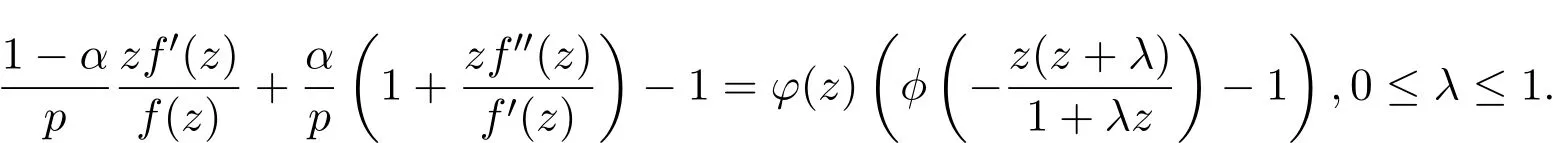
另外,根據引理3.3也可以得到(11)式和(12)式成立.綜上所述,定理3.2證畢.

注 3.1(1)在定理3.1和定理3.2中,令φ(z)≡1,得到文獻[7]中定理8的結論;

(2)在定理 3.1中,令p=1,α=0,得到文獻[12]中定理2.1的結論;

(3)在定理3.1和推論3.1中,令p=1,α=1,得到文獻 [12]中定理2.4和定理2.5的結論;

(4)在定理3.1和推論3.1中,令p=1,得到文獻[12]中定理2.10和定理2.12的結論.

定理 3.3如果 f(z)∈Lq,p(α,?),那么

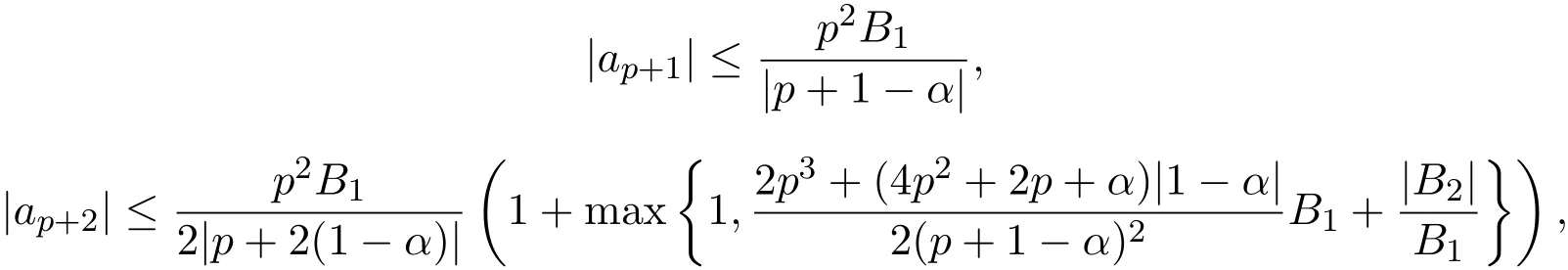
且對任何復數μ,有

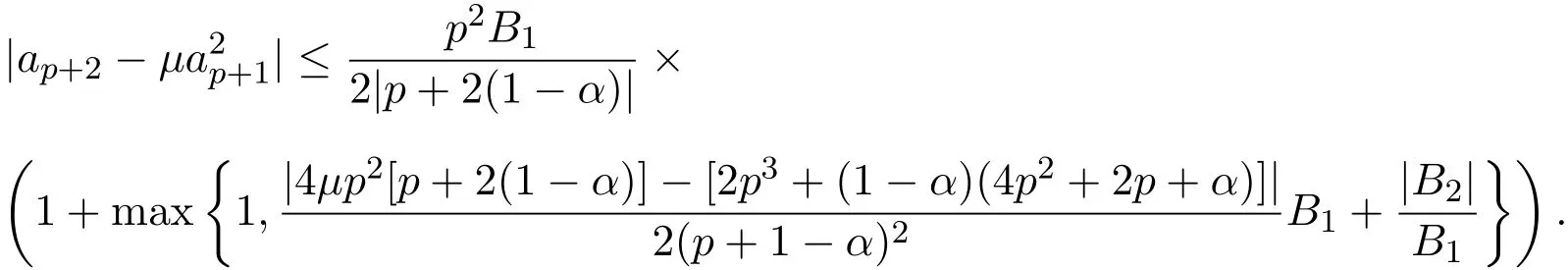
證明設 f(z)∈ Lq,p(α,?),則存在解析函數 φ(z)和 ω(z)滿足 |φ(z)|≤ 1,ω(0)=0和 |ω(z)|<1,使得

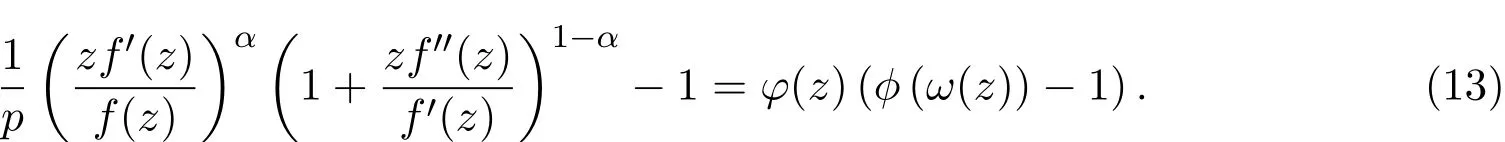
令β=1?α.將(1)式代入(13)式左側,通過計算分別可得

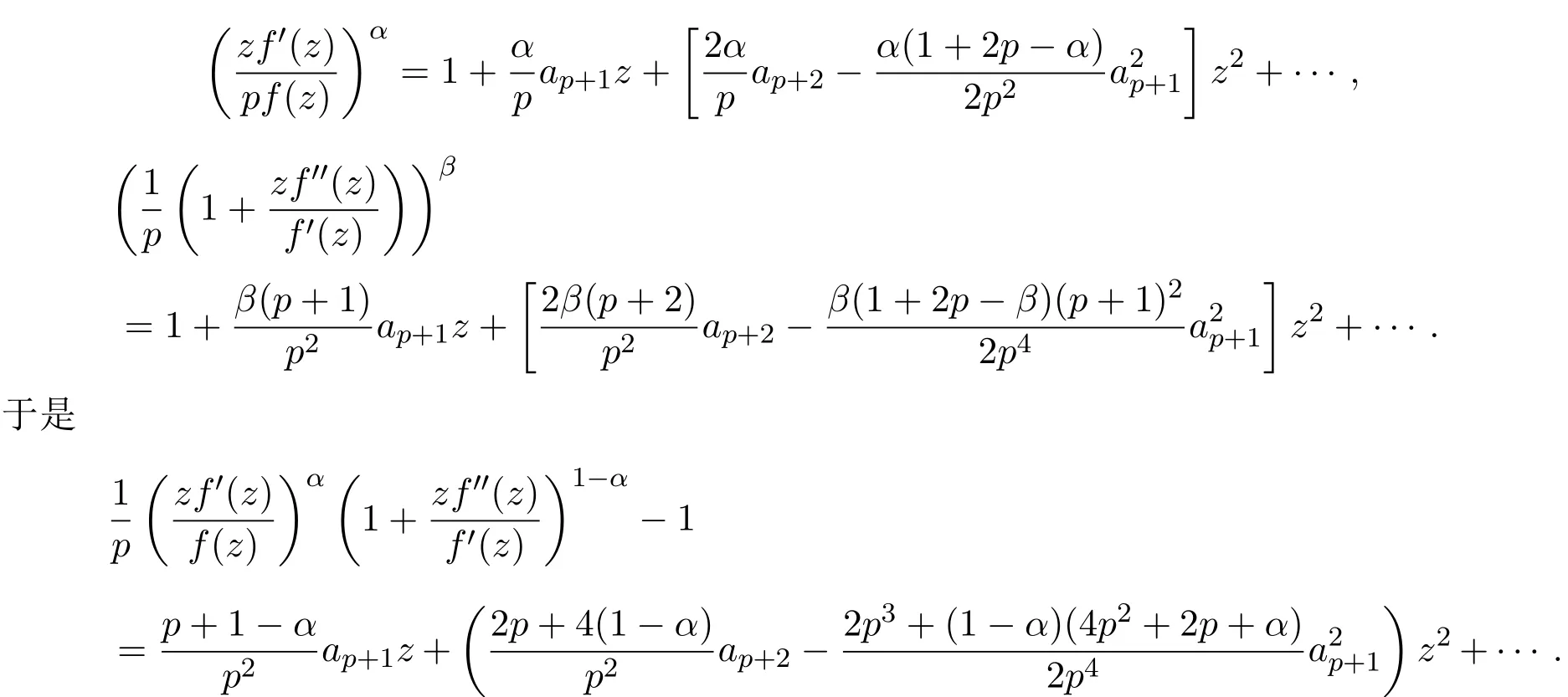
將上式和(6)式代入(13)式,比較兩邊同次冪的系數,得

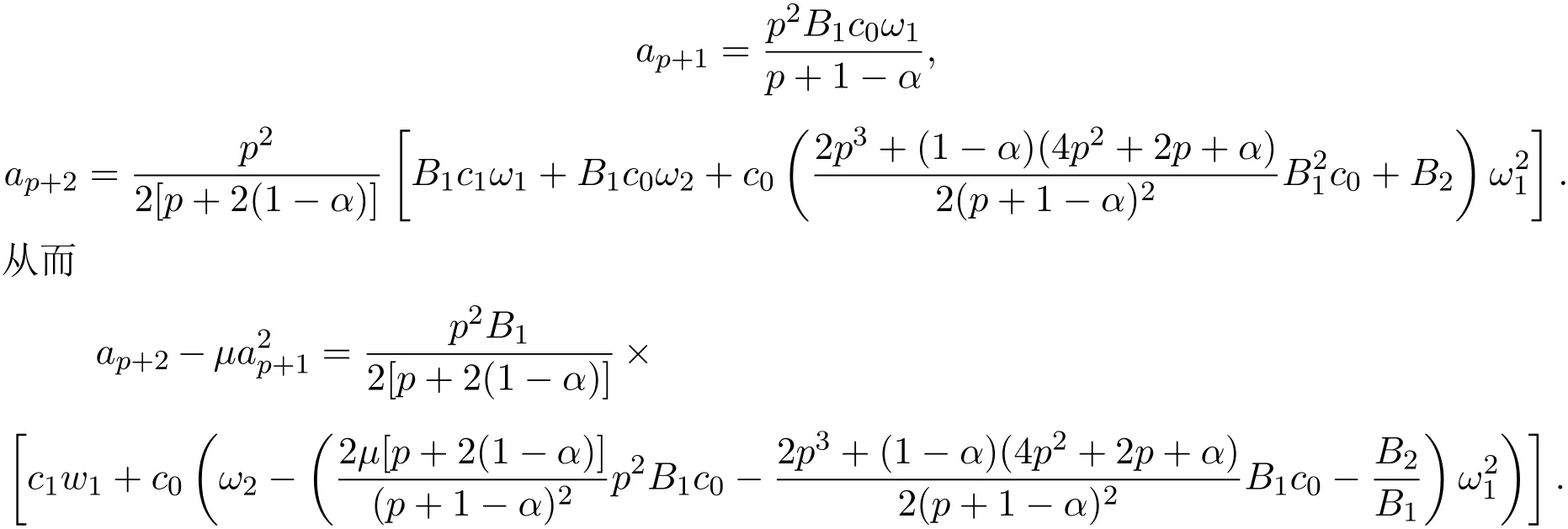
類似于定理3.1的證明,利用引理3.1和引理3.2,可知結論成立.因此,定理3.3證畢.

在定理3.3中,令ω(z)=z,得到如下結論.

推論 3.2如果f(z)∈Ap滿足

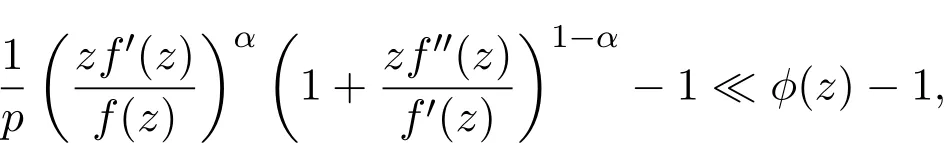
則

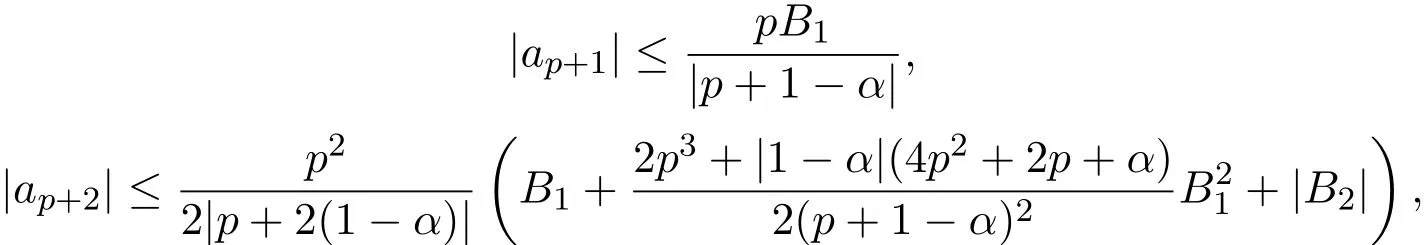
且對任何復數μ,有

定理 3.4如果 f(z)∈Lq,p(α,?),那么對任何實數 μ,有

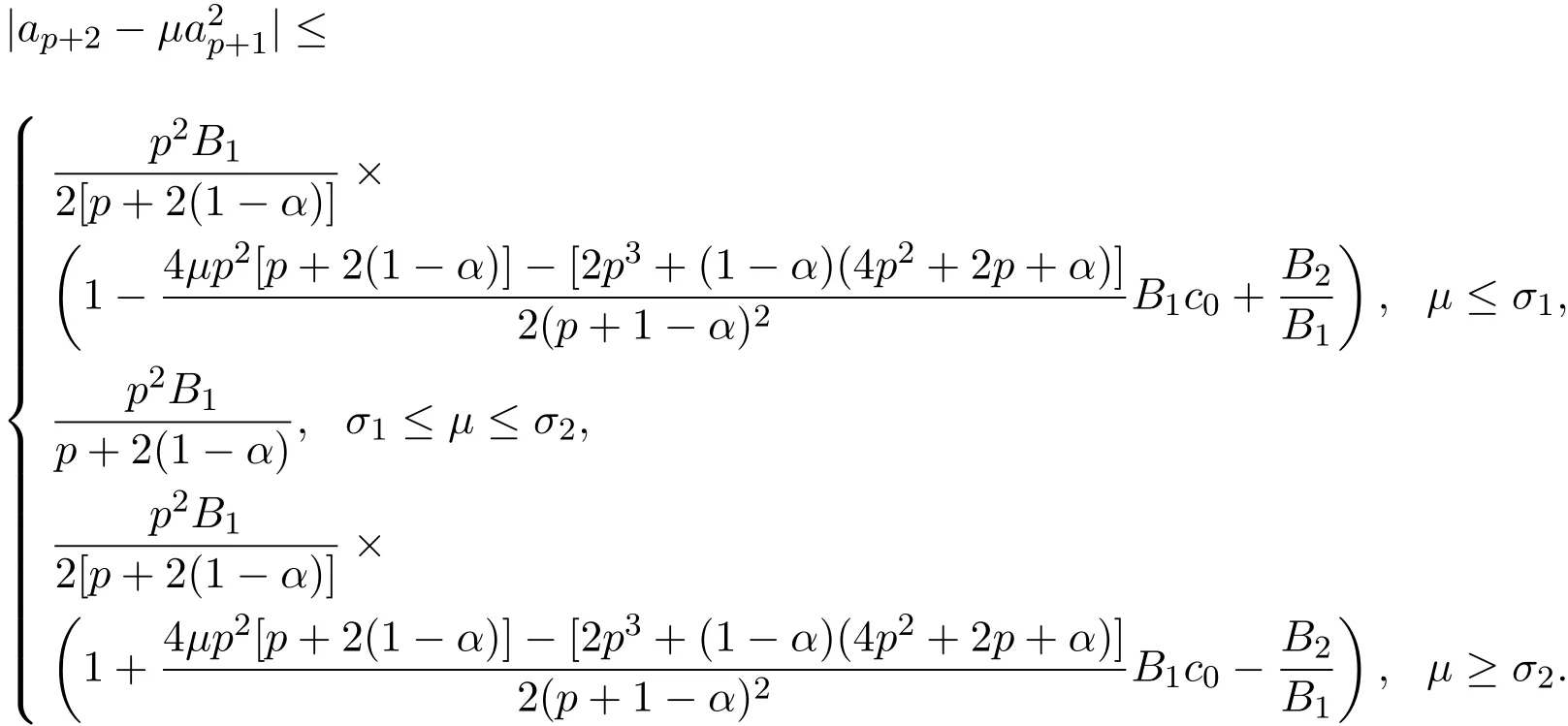
另外,當 σ1≤ μ ≤ σ3時,有

當 σ3≤ μ ≤ σ2時,有

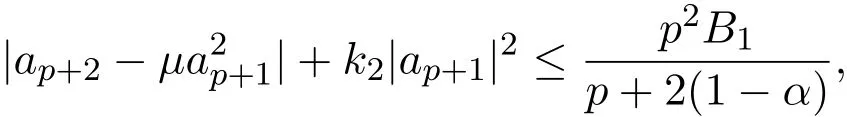
其中B2∈R,c0∈R,c0>0,

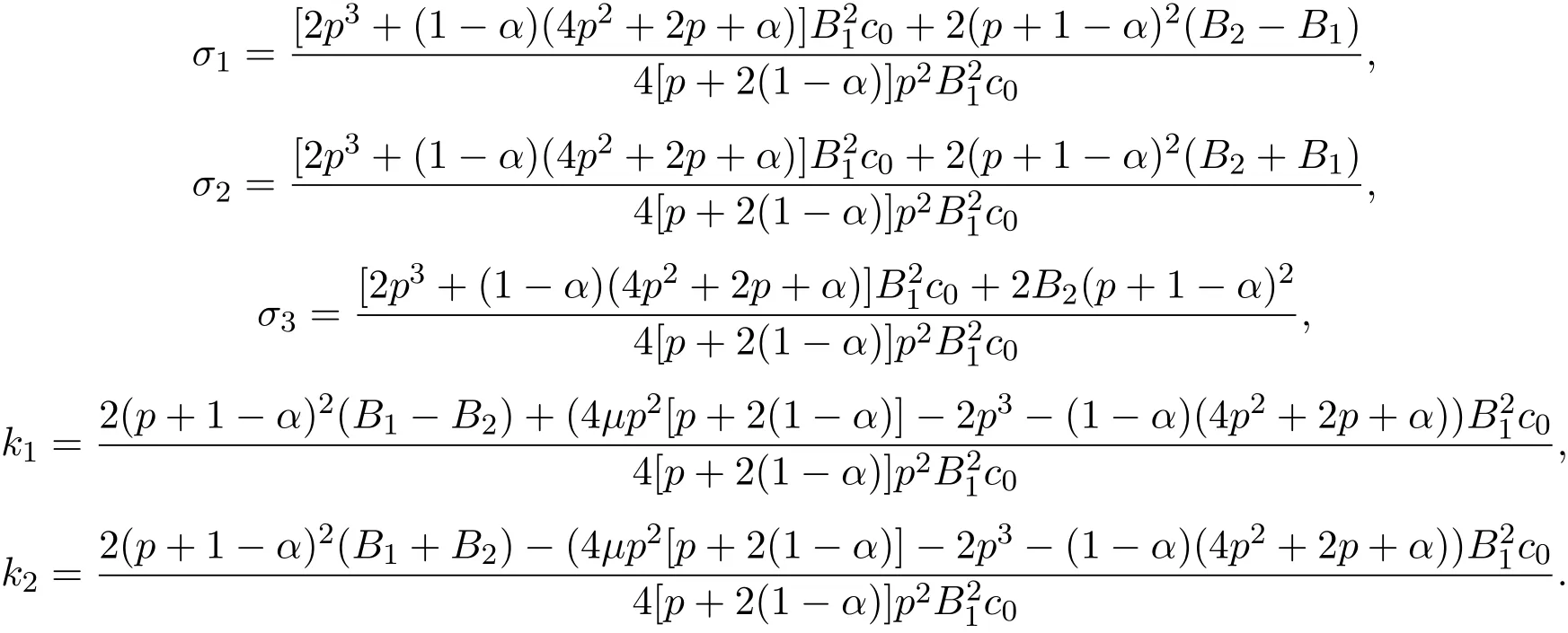
注 3.2(1)在定理3.3和定理3.4中,令φ(z)≡1,得到文獻[7]中定理7的結論;

(2)在定理3.3中和推論3.2中,令p=1,得到文獻[12]中定理2.13和定理2.15的結論.

定理 3.5如果 f(z)∈Rq,p(b,?),那么

且對任何復數μ,有

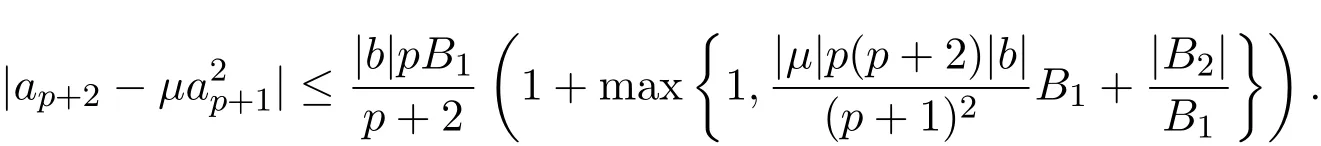
證明設 f(z)∈ Rq,p(b,?),則存在解析函數 φ(z)和 ω(z)滿足 |φ(z)|≤ 1,ω(0)=0和 |ω(z)|<1,使得

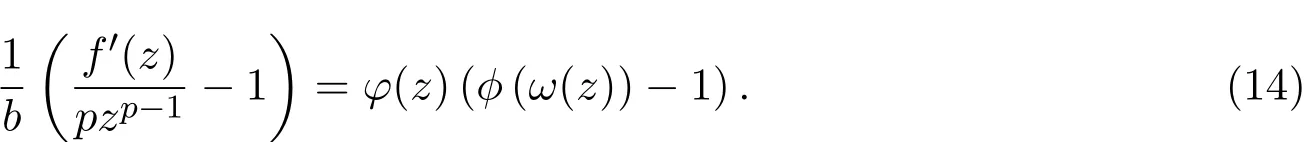
將(1)式代入(14)式左側,計算得

于是將上式和(6)式代入到(14)式,比較兩邊同次冪的系數,可得

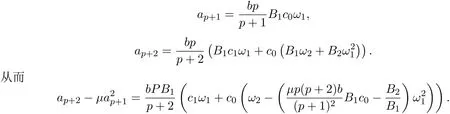
類似于定理3.1的證明,利用引理3.1和引理3.2,可知結論成立.因此,定理3.5證畢.

在定理3.5中,令ω(z)=z,得到如下結論.

推論 3.3如果f(z)∈Ap滿足:

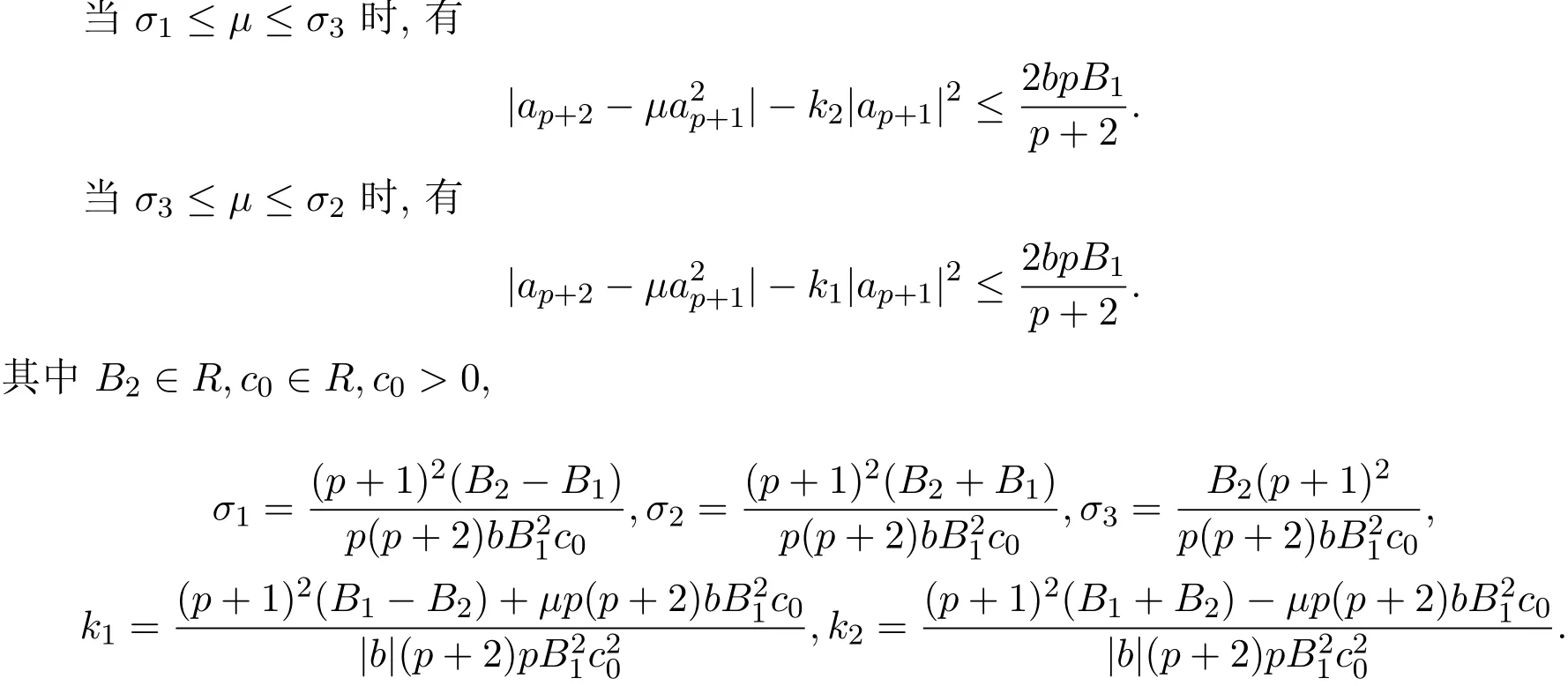
注 3.3(1)在定理3.5和定理3.6中,令φ(z)≡1,b≡1,得到文獻[7]中定理1的結論;

(2)在定理3.5中,令φ(z)≡1,得到文獻[7]中定理3和定理4的結論;

(3)在定理3.5和推論3.3中,令p=1,b=1,得到文獻[12]中定理2.6和定理2.7的結論;

(4)在定理3.5中,令p=1,得到文獻[12]中推論2.8的結論.

4 Hadamard卷積在 Fekete-Szeg問題上的應用

最后,給出 Hadamard 卷積在函數類 Mq,p(α,?),Lq,p(α,?)和 Rq,p(b,?)的 Fekete-Szeg¨o 問題上的應用.

定理4.1設

其中B2∈R,c0∈R,c0>0,

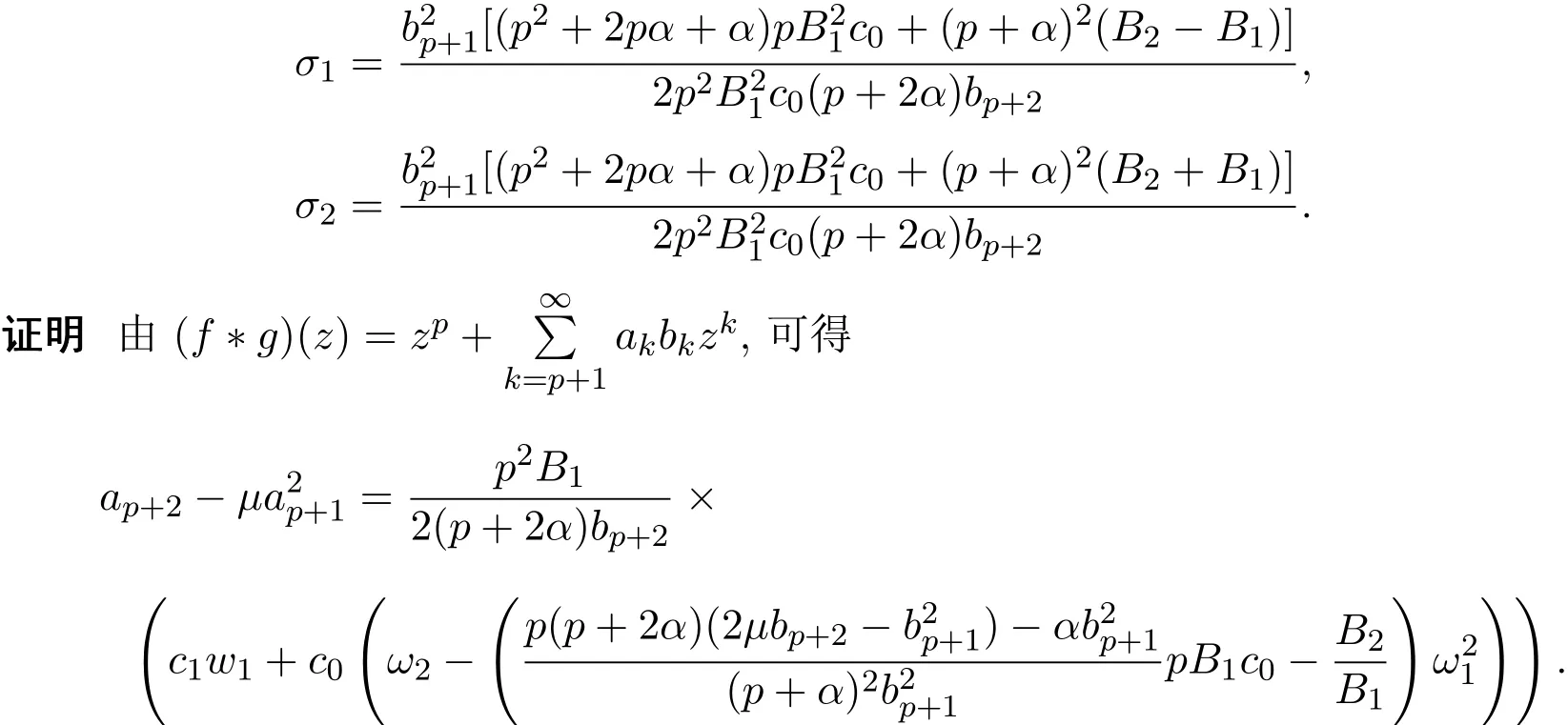
于是類似于定理3.1和3.3的證明,可得定理4.1的結論.因此,定理4.1證畢.

利用相同方法可以證明下面的定理4.2和定理4.3.

定理4.2設

[1]Fekete M,SzegG.Eine bermerkung uberungerade schlichte function[J].Journal of the London Mathematical Society,1933,8(2):85-89.

[2]Kanas S,Lecko A.On The Fekete-Szeg¨o problem and the domain of convexity for a certain class of univalent functions[J].Zeszyty Naukowe Politechniki Rzezowskiej,1990(10):49-57.

[3]Kwo O S,Cho N E.On The Fekete-Szeg¨o problem for certain analytic functions[J].Journal of the Korea Society of Mathematical Education B,2003,10(4):265-271.

[4]高純一.近于凸函數族的Fekete-Szeg¨o問題[J].數學年刊,1994,15A(6):650-656.

[5]李宗濤,劉名生.一類解析函數的系數泛函[J].華南師范大學學報,2005,3:86-91.

[6]周從會.關于α-凸函數的Fekete-Szeg¨o不等式[J].純粹數學與應用數學,2010,26(1):51-55.

[7]Mohd M M,Darus M.Fekete-Szeg¨o problems for quasi-subordination classes[J].Journal of Abstract and Applied Analysis,2012,3(2):1-14.

[8]Srutha B,Prema S.Coefficient problem for certain subclass of analytic functions using quasi-subordination[J].Journal of Mathematics and Decision sciences,2013,13(6):47-53.

[9]Srutha B,Lokesh P.Fekete-Szeg¨o problem for certain subclass of analytic univalent function using quasisubordination[J].Mathematica Aeterna.,2013,3(3):193-199.

[10]El-Ashwah R,Kanas S.Fekete-Szeg¨o inequalities for quasi-subordination functions classes of complex order[J].Journal of Kyungpook Mathematics,2015,55:679-688.

[11]Goyal S P,Kumar Rakesh.Coefficient estimates and quasi-subordination properties associated with certain subclass of analytic and bi-univalent functions[J].Math.Salovaca,2016,3:25-32.

[12]Ali R M,Ravichandran V,NSeenivasagan.Coefficient bounds for P-valent functions[J].Applied Mathematics and Computation,2007,187(1):35-46.

[13]Robertson M S.Quasi-subordination and coefficient conjectures[J].Bulletin of the American Mathematical Society,1970,76:1-9.

[14]Keogh F R,Merkes E P.A coefficient inequality for certain classes of analytic functions[J].Proc.Amer.Math.Soc.,1969,20:8-12.

[15]Ma W C,Minda D.A uni fi ed treatment of some special classes of univalent functions[J].In Proceedings of the Conference on Complex Analysis,1994,1:157-169.

On coefficient estimates for some subclasses of P-valent functions

Aoen1,Li Shuhai1,Siqinqimuge2
(1.School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China;2.School of Computer and Information Engineering,Chifeng University,Chifeng 024000,China)

We introduce some new subclasses of p-valent analytic functions de fi ned by quasi-subordination.The coefficient estimates of the classes is discussed by using the fundamental inequalities of analytic functions and analytical techniques.The accurate results are obtained,which generalize some related results.And the applications of Fekete-Szeg¨o problem of the functions with Hadamard convolution are proved.

analytic functions,p-valent functions,quasi-subordination,coefficient estimate,Fekete-Szegproblem,Hadamard convolution

O174.51

A

1008-5513(2017)03-0260-14

10.3969/j.issn.1008-5513.2017.03.006

2017-03-22.

國家自然科學基金(11560001);內蒙古自然科學基金(2014MS0101);內蒙古高校科學研究項目(2015NJZY240).

敖恩(1980-),碩士,副教授,研究方向：復分析及其應用.

2010 MSC:41A35