碰摩拉桿轉子非線性動力學響應特性
胡 亮, 柳亦兵, 趙 立,2, 周 超
(1.華北電力大學 電站設備狀態監測與控制教育部重點實驗室,北京 102206;2.北京能源投資集團有限公司,北京 100022)
?
碰摩拉桿轉子非線性動力學響應特性
胡 亮1, 柳亦兵1, 趙 立1,2, 周 超1
(1.華北電力大學 電站設備狀態監測與控制教育部重點實驗室,北京 102206;2.北京能源投資集團有限公司,北京 100022)
對定點碰摩故障狀態下拉桿轉子的非線性動力學響應特性進行了研究.將輪盤之間的非線性接觸特性等效為具有非線性抗彎剛度的彈簧,基于達朗貝爾原理建立了考慮輪盤之間非線性接觸特性、非線性油膜力以及碰摩力作用的拉桿轉子軸承系統運動方程,并采用數值積分方法對運動方程進行求解,分析了系統位移響應隨輪盤的轉速和碰摩剛度等參數變化的規律. 結果表明:輪盤之間的非線性接觸對系統位移響應特性影響較大;隨著輪盤轉速的升高,系統呈非線性特性;碰摩剛度是影響拉桿轉子軸承系統運動狀態的重要因素,若增大碰摩剛度,系統的運動狀態將發生改變.
拉桿轉子; 碰摩; 非線性動力學; 分岔; 響應特性; 達朗貝爾原理
轉子軸承系統是旋轉機械的核心部件,在設計汽輪機等透平機械的轉子軸承系統時,為提高透平的效率,通常將轉子與靜子的間隙設計得很小.轉子與靜子較小的間隙使得轉子與靜子發生碰摩的概率隨著轉速的升高而增大,碰摩會使轉子與靜子間的間隙增大、葉片折斷,嚴重時會造成設備損壞失效.因此,對轉子軸承系統碰摩的研究具有重要的現實意義.
國內外學者已對轉子軸承系統的碰摩現象進行了大量研究,并取得了顯著的成果[1-4].馬輝等[5]對目前轉子軸承系統碰摩故障實驗研究的進展進行了綜述,指出了碰摩故障實驗研究的發展方向.姚紅良等[6]提出了一種基于諧波分量的轉子軸承系統碰摩故障的定量診斷方法,并通過數值仿真和實驗研究證明了該方法的有效性.Wang等[7]對滑動軸承支承的轉子軸承系統碰摩故障的非線性動力學響應特性進行了分析.Abu-Mahfouz等[8]通過數值分析和演化算法,研究了碰摩轉子軸承系統的非線性動力學響應特性,為旋轉機械的故障診斷和狀態監測提供了指導.
目前,對轉子軸承系統碰摩故障的研究都是基于整體轉子.拉桿轉子在重型燃氣輪機和航空發動機中應用比較廣泛.拉桿轉子由軸向拉伸的拉桿將各輪盤壓緊組成,在結構上具有不連續性.輪盤之間的接觸特性對拉桿轉子的動力學響應特性影響較大.Hei等[9-10]將輪盤之間的接觸特性等效為具有立方非線性的抗彎彈簧,研究了滑動軸承支承的拉桿轉子的非線性動力學特性.程禮等[11-12]針對盤式拉桿轉子中出現的雙穩態振動故障現象,將拉桿轉子的接觸效應等效為具有非線性抗彎剛度的彈簧,建立了拉桿轉子的運動方程,并采用預估校正算法和同倫算法對方程進行求解,結果表明非線性接觸是引起盤式拉桿轉子出現雙穩態特征的主要原因.
針對燃機用拉桿轉子在高速下可能發生碰摩的問題,筆者研究了在定點碰摩力作用下拉桿轉子的非線性動力學響應特性.將拉桿固定的輪盤之間的接觸效應等效為一個具有非線性抗彎剛度的彈簧,建立定點碰摩故障時拉桿轉子軸承系統的運動方程,采用數值積分方法對方程進行求解,得到系統在不同參數下的非線性動力學響應特性.
1 動力學建模
拉桿轉子軸承系統的結構示意圖見圖1,該轉子中間的2個輪盤用拉桿連接在一起,轉子兩端支撐軸承為動壓滑動軸承.基于如下假設對系統進行簡化:(1)拉桿轉子兩端采用相同的滑動軸承支承,滑動軸承滿足短軸承理論;(2)碰摩發生在輪盤1x方向固定點處,且產生徑向瞬時沖擊力,碰摩過程中產生的熱效應忽略不計;(3)拉桿轉子輪盤之間的接觸效應等效為具有非線性抗彎剛度的彈簧;(4)拉桿轉子的扭轉和軸向振動很小,可以忽略不計,輪盤與滑動軸承通過一個無質量的彈性軸連接.

圖1 拉桿轉子軸承系統示意圖Fig.1 Schematic diagram of the rod fastening rotor bearing system
1.1 軸承的非線性油膜力
動壓滑動軸承的非線性油膜力可以通過求解雷諾方程得到.采用基于短軸承理論的Capone非線性油膜力模型[13],無量綱非線性油膜力公式為:
(1)
其中,
(2)
(3)
(4)
(5)
式中:fx、fy為無量綱非線性油膜力在x方向和y方向的分量;X、Y為滑動軸承處軸頸在x方向和y方向的無量綱位移,X=x/c,Y=y/c,c為滑動軸承徑向間隙.
1.2 碰摩力
圖2給出了拉桿轉子輪盤1發生碰摩的部位及碰摩力的方向.假設碰摩產生的結構變形是線性的,且碰摩只發生在x方向,則碰摩產生的切向摩擦力PT符合庫倫摩擦定律.
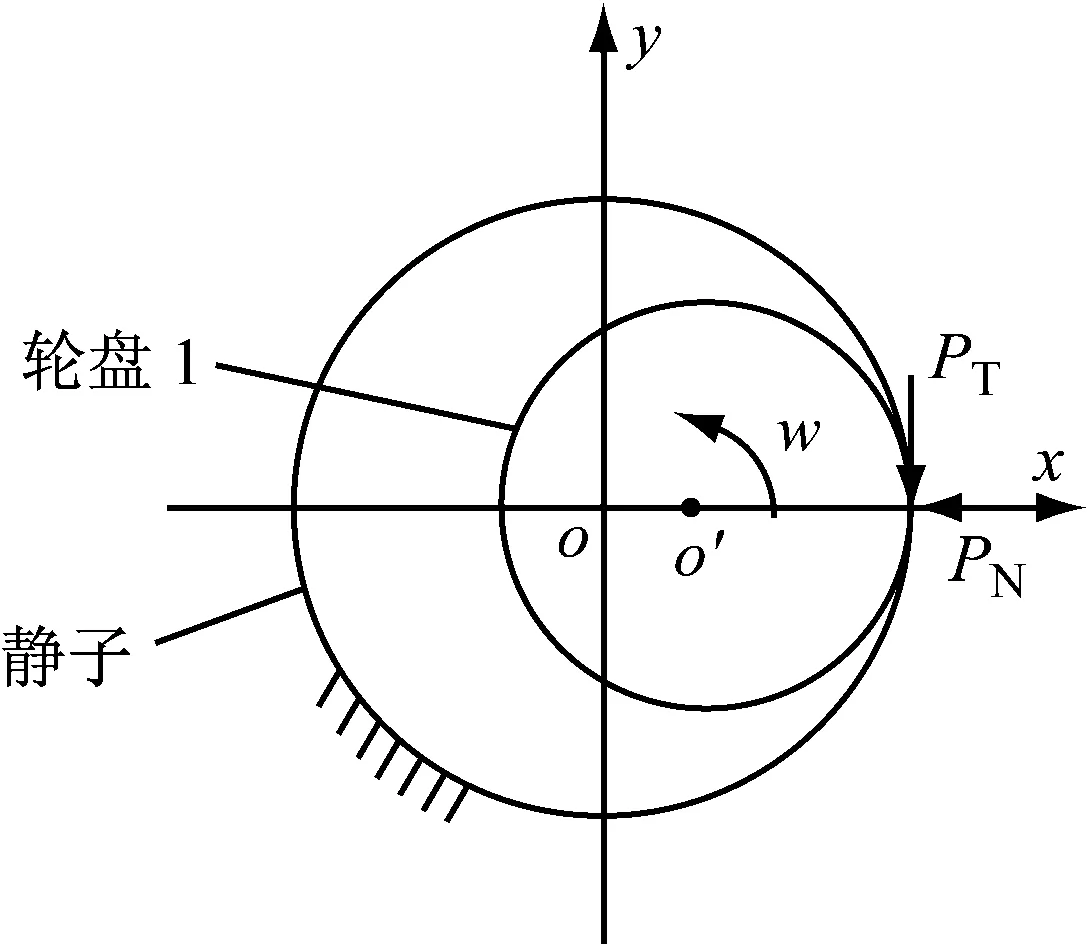
圖2 碰摩力示意圖Fig.2 Schematic diagram of the rub-impact force
根據以上假設,徑向碰摩力PN和切向碰摩力PT可表示為:
(6)

將徑向碰摩力PN和切向碰摩力PT在x方向和y方向進行分解:
(7)
1.3 定點碰摩拉桿轉子動力學方程
將圖1所示的拉桿轉子軸承系統模型簡化為集中質量模型.設拉桿轉子在軸承處的集中質量為m,輪盤1、輪盤2的集中質量分別為m1和m2,二者偏心距分別為e1和e2,φ為二者不平衡質量偏心距之間的矢量夾角.拉桿轉子在軸承處的阻尼系數為c1,在輪盤處的阻尼系數為c2,在接觸層的阻尼系數為c3,無質量彈性軸的剛度為k.滑動軸承軸頸處的坐標為(xb,yb),(x1,y1)、(x2,y2)分別為輪盤1和輪盤2的坐標.將拉桿轉子輪盤之間的接觸等效為具有非線性抗彎剛度的彈簧,彈簧的恢復力為f=k1x+k2x3,其中x為兩盤之間的相對位移,k1為線性剛度系數,k2為非線性剛度系數[12].
根據達朗貝爾原理,建立考慮定點碰摩力下拉桿轉子軸承系統的運動方程組:
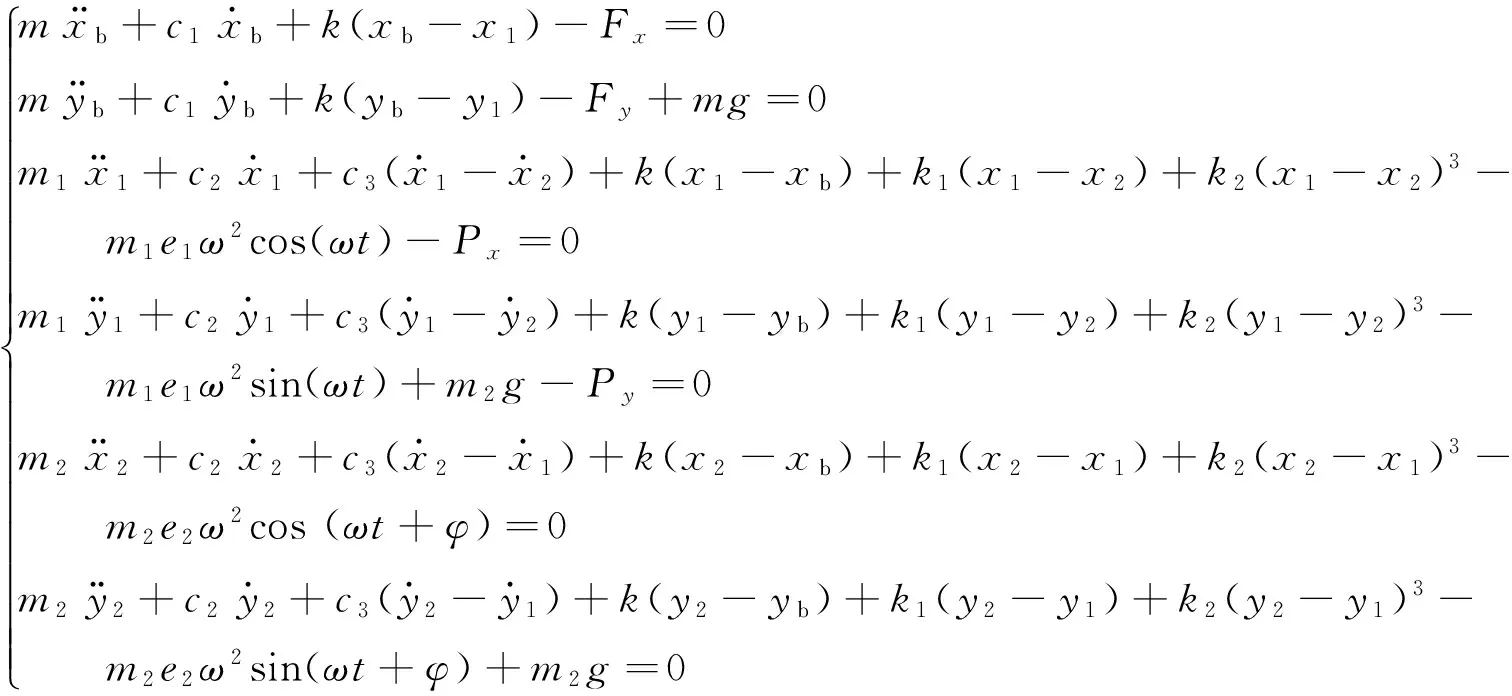
(8)
其中Fx、Fy為非線性油膜力在x方向和y方向的分量.定義無量綱變量:Xb=xb/c,Yb=yb/c,X1=x1/c,Y1=y1/c,X2=x2/c,Y2=y2/c,系統的無量綱時間為τ,τ=wt.
方程(8)的無量綱形式為:
(9a)
(9b)
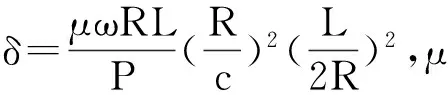
2 數值計算結果及討論

2.1 轉速的影響
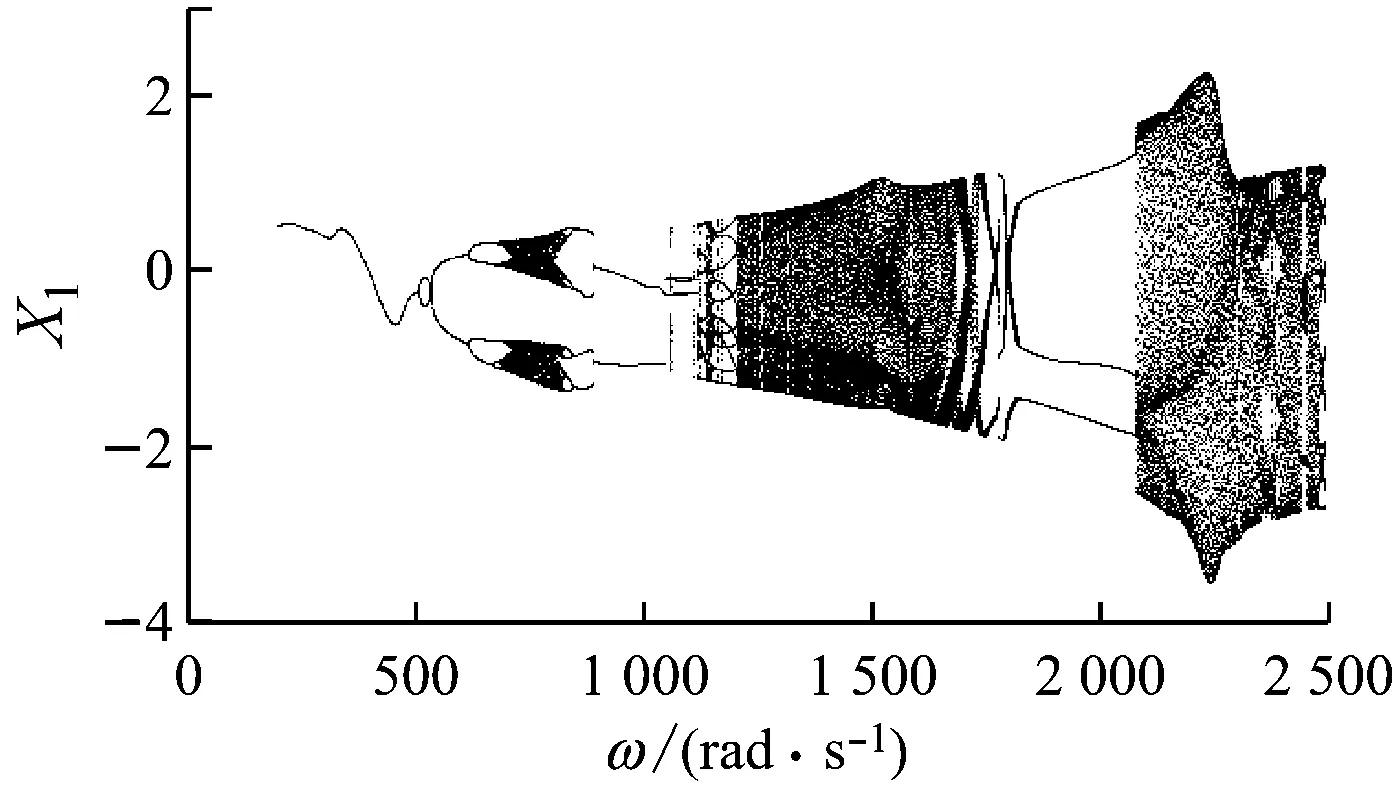
圖3(a)為考慮輪盤間非線性接觸的輪盤1在x方向的位移響應隨轉速變化的分岔圖.作為對比,圖3(b)為不考慮輪盤間非線性接觸(整體轉子)的位移響應隨轉速變化的分岔圖.從圖3可以看出,輪盤之間的非線性接觸對定點碰摩轉子軸承系統在x方向的位移響應產生較大影響.如圖3(a)所示,隨著轉速升高,系統呈現出豐富的非線性特性,系統運動狀態在周期1、多周期、擬周期、混沌運動狀態之間轉變.
結合分岔圖反映的不同轉速下幾種典型的轉子響應狀態,對各個狀態下的Poincaré圖和軸心軌跡圖特征進行討論,結果如圖4和圖5所示.
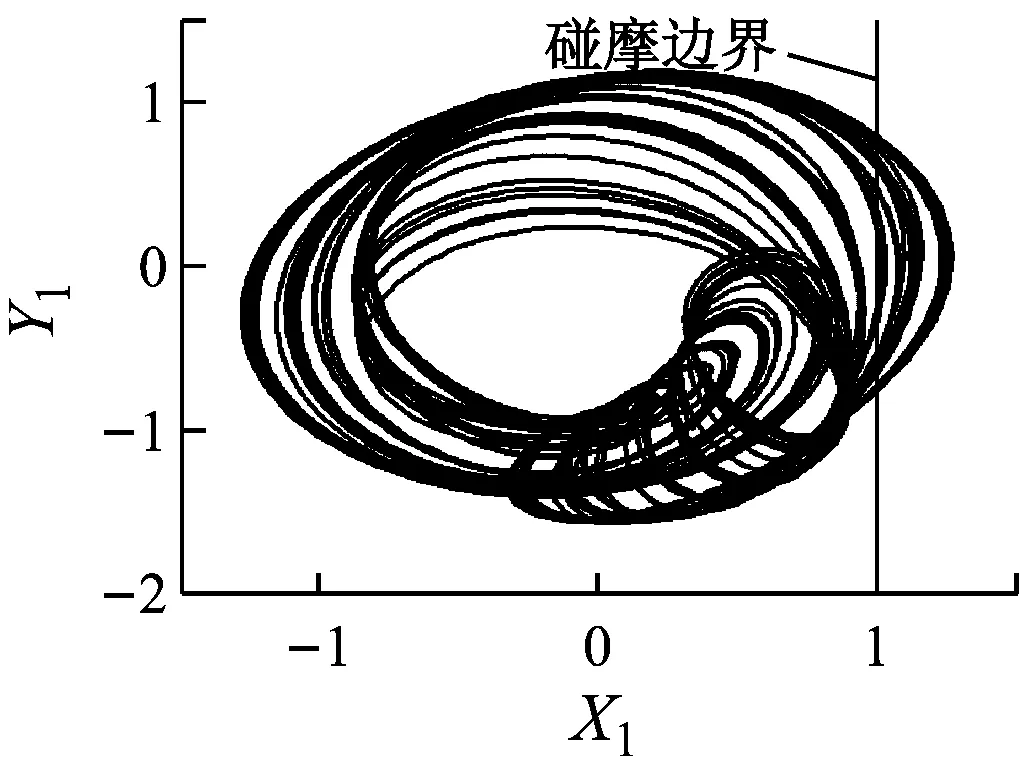
由圖4和圖5可知,當轉速小于507 rad/s時,系統保持穩定的周期1運動,在Poincaré圖中表現為一個孤立的點,如圖4(a)所示,此時不發生碰摩,則非線性油膜力是影響系統狀態的重要因素.當轉速達到507 rad/s時,系統分岔為周期2運動(見圖4(b)和圖5(b)).繼續升高轉速,當轉速達到659 rad/s時,輪盤的軸心軌跡超出碰摩邊界,系統發生碰摩,在碰摩力和非線性油膜力的共同作用下系統經倍周期分岔進入混沌運動(見圖4(c)、圖4(d)、圖5(c)和圖5(d)).
(a) 考慮輪盤間非線性接觸
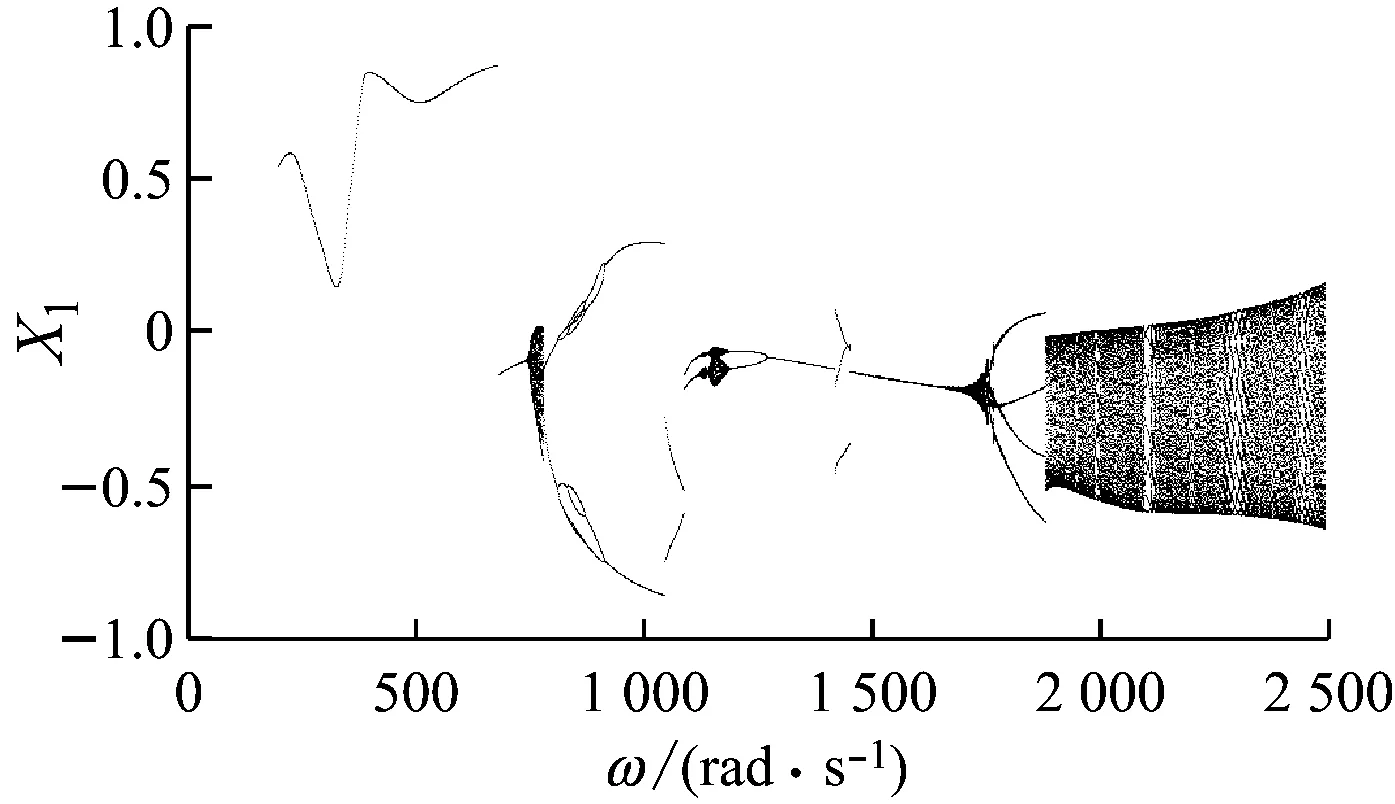
(b) 不考慮輪盤間非線性接觸圖3 x方向的位移響應隨轉速變化的分岔圖Fig.3 Bifurcation diagram of displacement response in xdirection changing with rotating speed
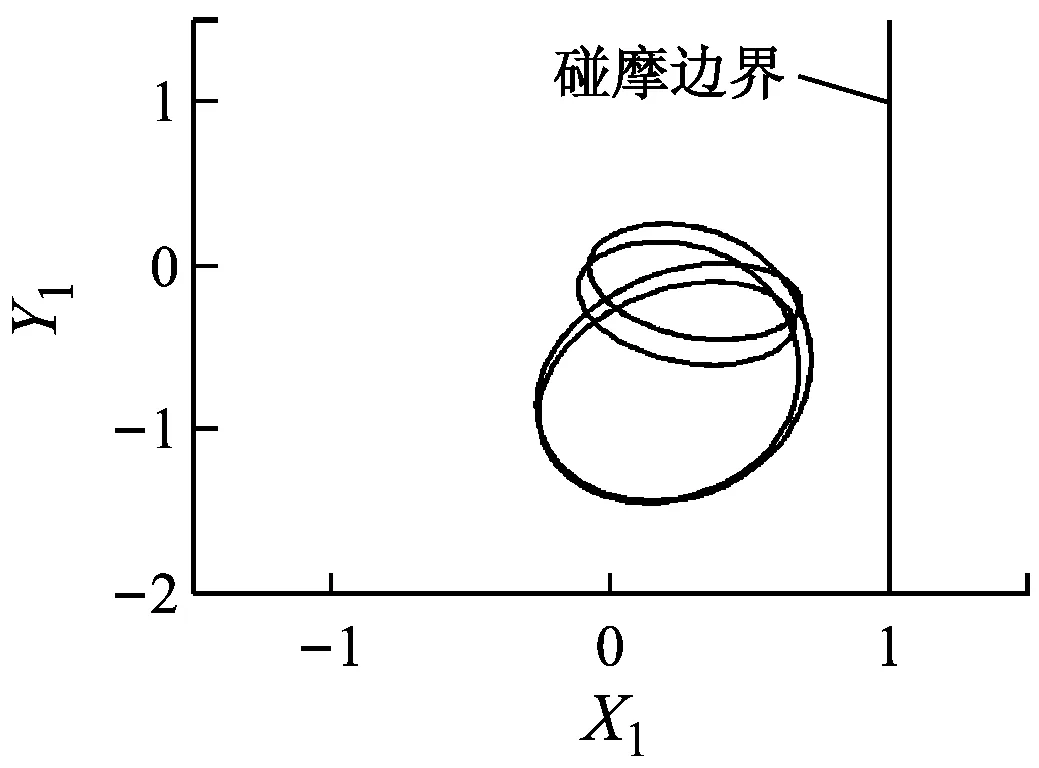
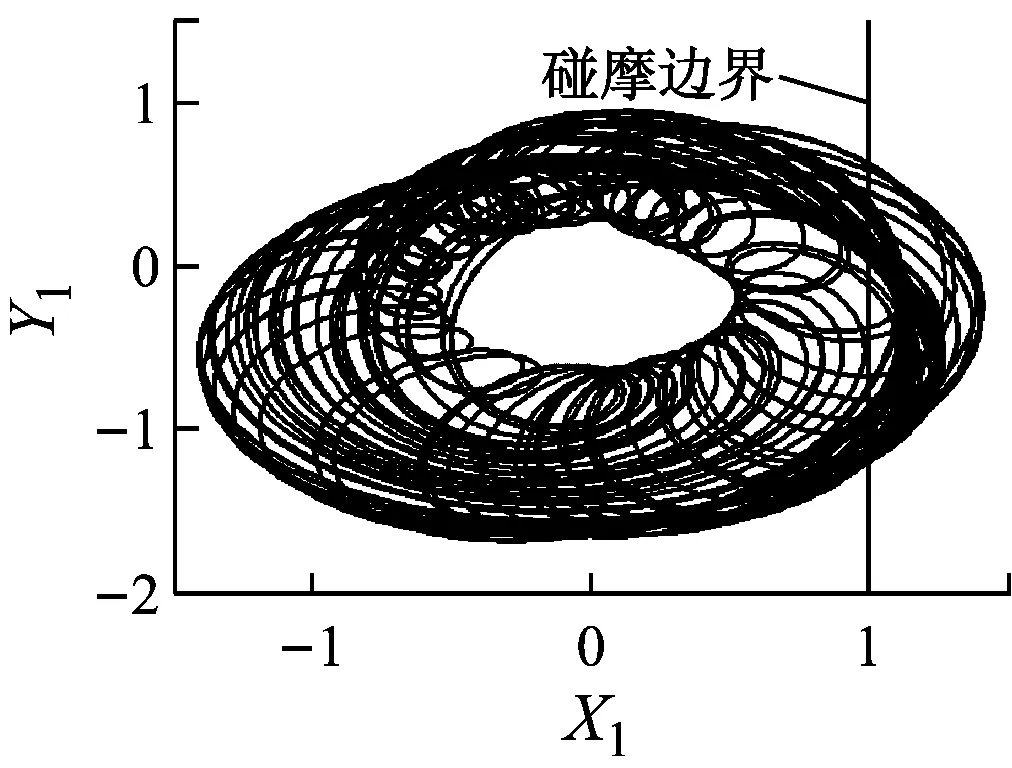
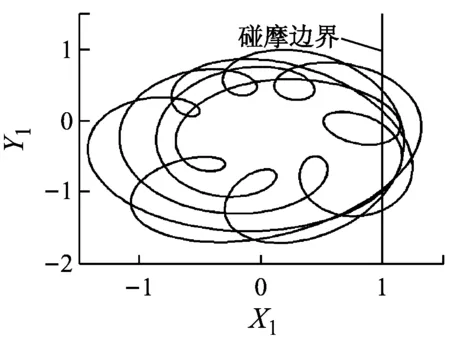
繼續升高轉速,碰摩力逐漸增加,當轉速在825~1 047 rad/s內時,隨轉速的升高系統出現倒分岔現象.當轉速在1 047~1 109 rad/s內時,系統保持周期4運動,Poincaré圖中表現為4個孤立的點(如圖4(e)所示),此時輪盤軸心軌跡未超出碰摩邊界,碰摩消失.當轉速繼續升高且在1 109~2 500 rad/s內變化時,系統再次發生碰摩,系統經概周期運動、周期1運動、概周期運動、周期3運動后,最終進入概周期運動狀態.
2.2 碰摩剛度的影響
拉桿轉子軸承系統的碰摩剛度是影響系統位移響應特性的一個重要參數.圖6給出了轉速為2 113 rad/s時,定子剛度在0~3×107N/m內,輪盤在x方向的位移響應隨碰摩剛度變化的分岔圖.圖7(a)給出了碰摩剛度kc=1.5×107N/m和2.5×107N/m時,輪盤軸心軌跡圖和Poincaré圖.
由圖6可知,當系統轉速為2 113 rad/s時,系統運動狀態隨碰摩剛度的變化發生變化.碰摩剛度在0~1.99×107N/m內變化時,系統主要表現為擬周期運動狀態.圖7(a)中,Poincaré圖表現為一個近似封閉的環,表明此時系統處于擬周期運動狀態.當碰摩剛度在1.99×107~3×107N/m內時,系統處于周期3運動狀態.圖7(b)中,Poincaré圖表現為3個孤立的點,表明此時系統處于周期3運動狀態.
綜上所述,碰摩剛度對轉子的運動狀態有較大影響,隨著碰摩剛度的增加,系統的運動狀態將發生改變.
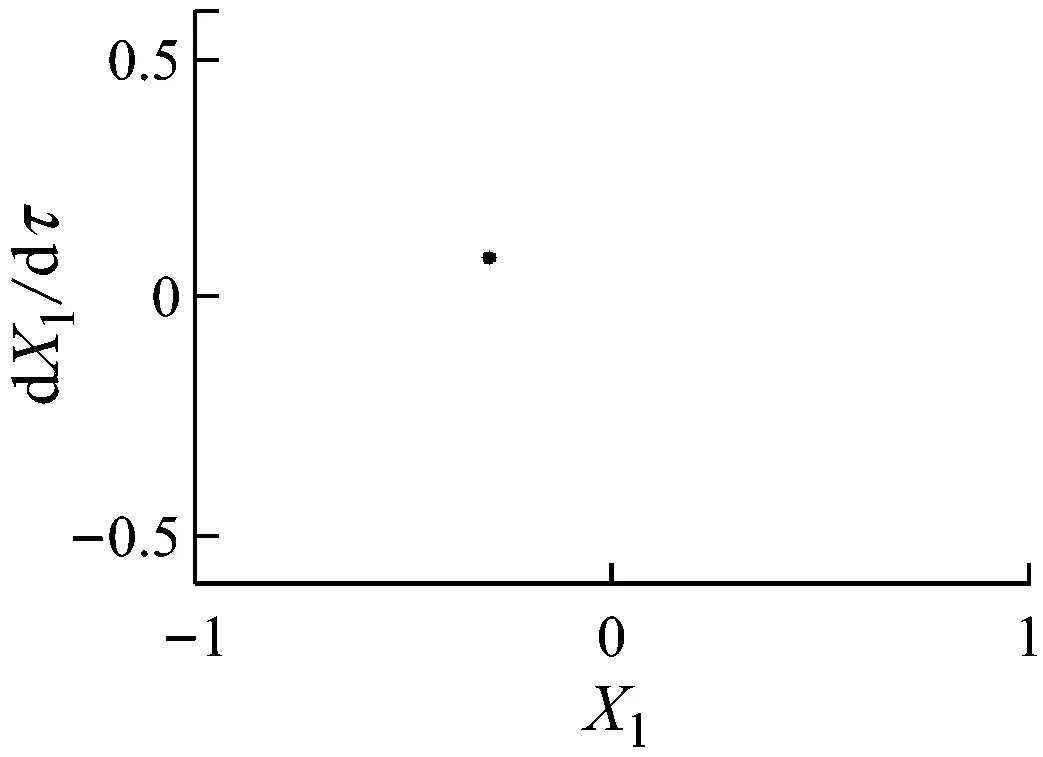
(a) ω=490 rad/s
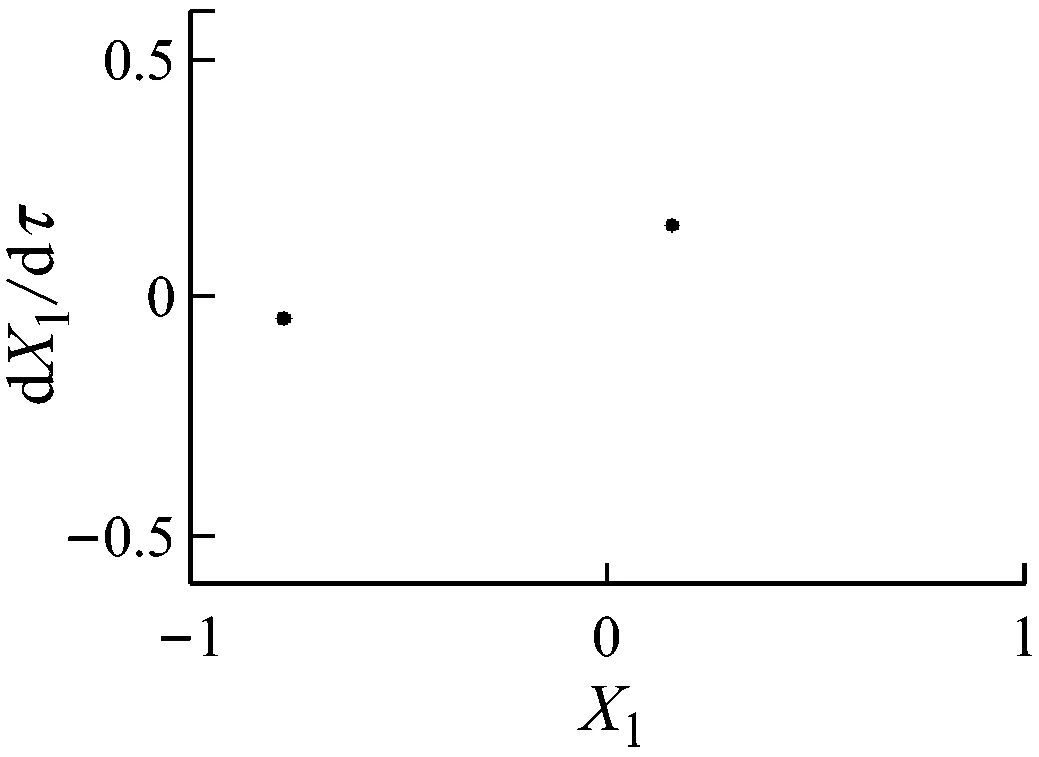
(b) ω=593 rad/s
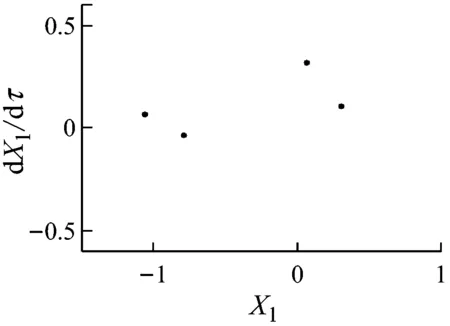
(c) ω=659 rad/s
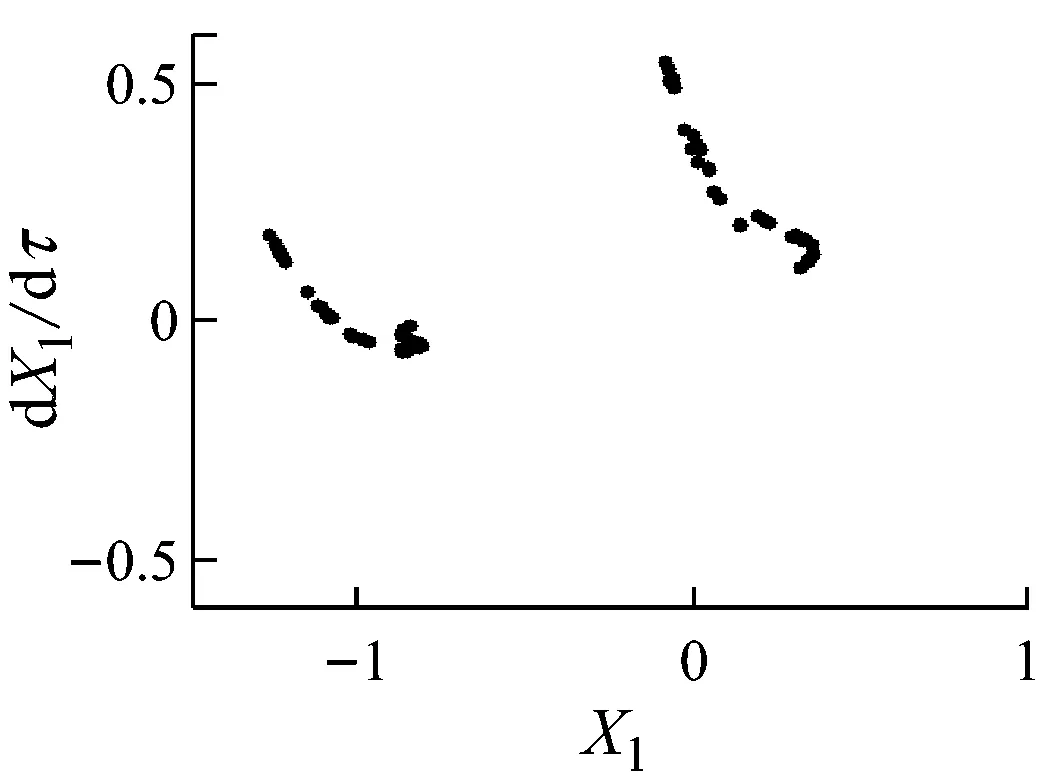
(d) ω=756 rad/s

(e) ω=1 082 rad/s
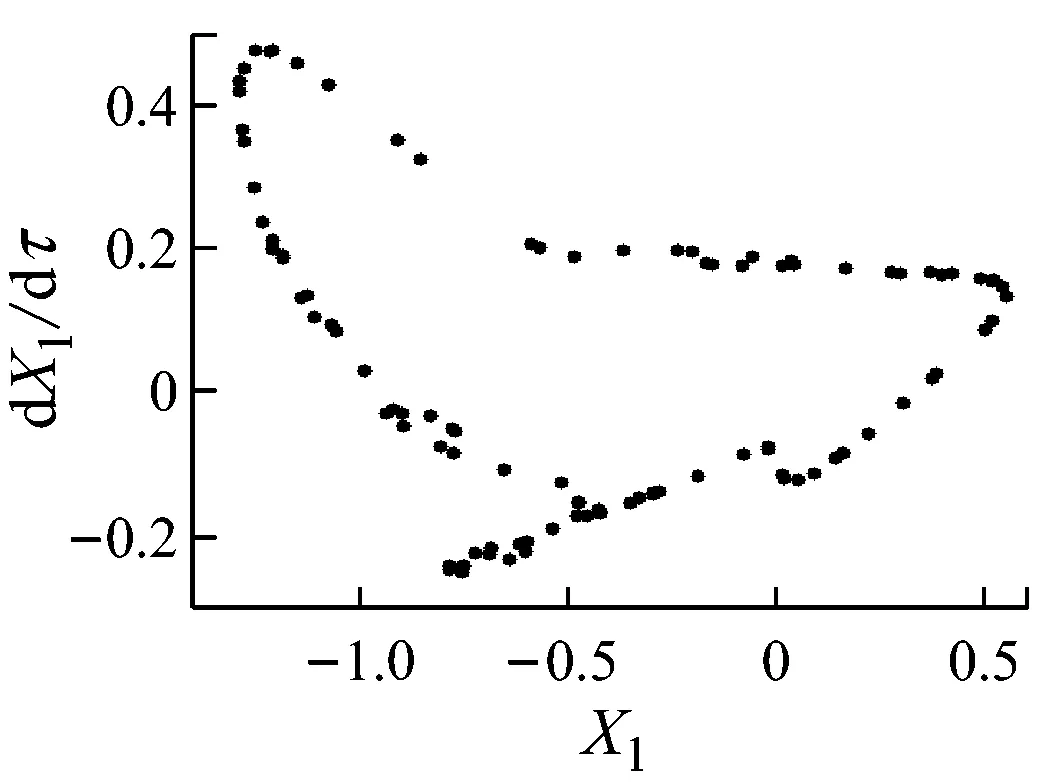
(f) ω=1 145 rad/s

(g) ω=1 191 rad/s
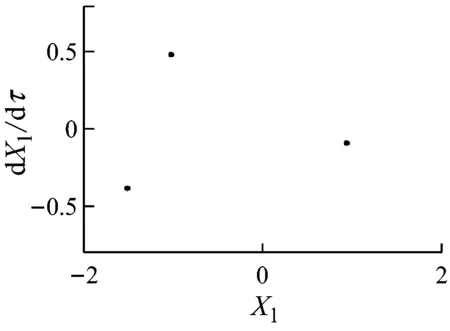
(h) ω=1 881 rad/s

(i) ω=2 143 rad/s圖4 不同轉速時的Poincaré圖Fig.4 Poincaré maps at different rotating speeds

(a) ω=490 rad/s
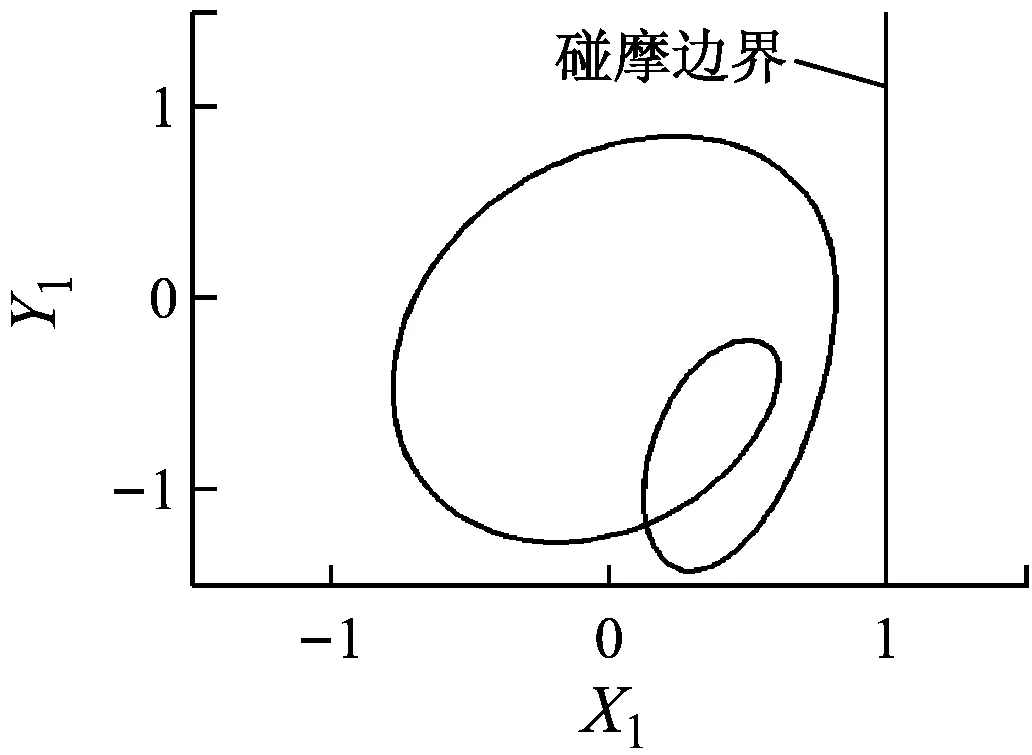
(b) ω=593 rad/s

(c) ω=659 rad/s
(d) ω=756 rad/s
(e) ω=1 082 rad/s
(f) ω=1 145 rad/s
(g) ω=1 191 rad/s
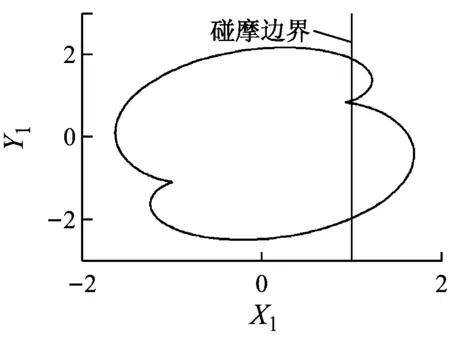
(h) ω=1 881 rad/s

(i) ω=2 143 rad/s圖5 不同轉速時的軸心軌跡圖Fig.5 Axis trajectory diagrams at different rotating speeds
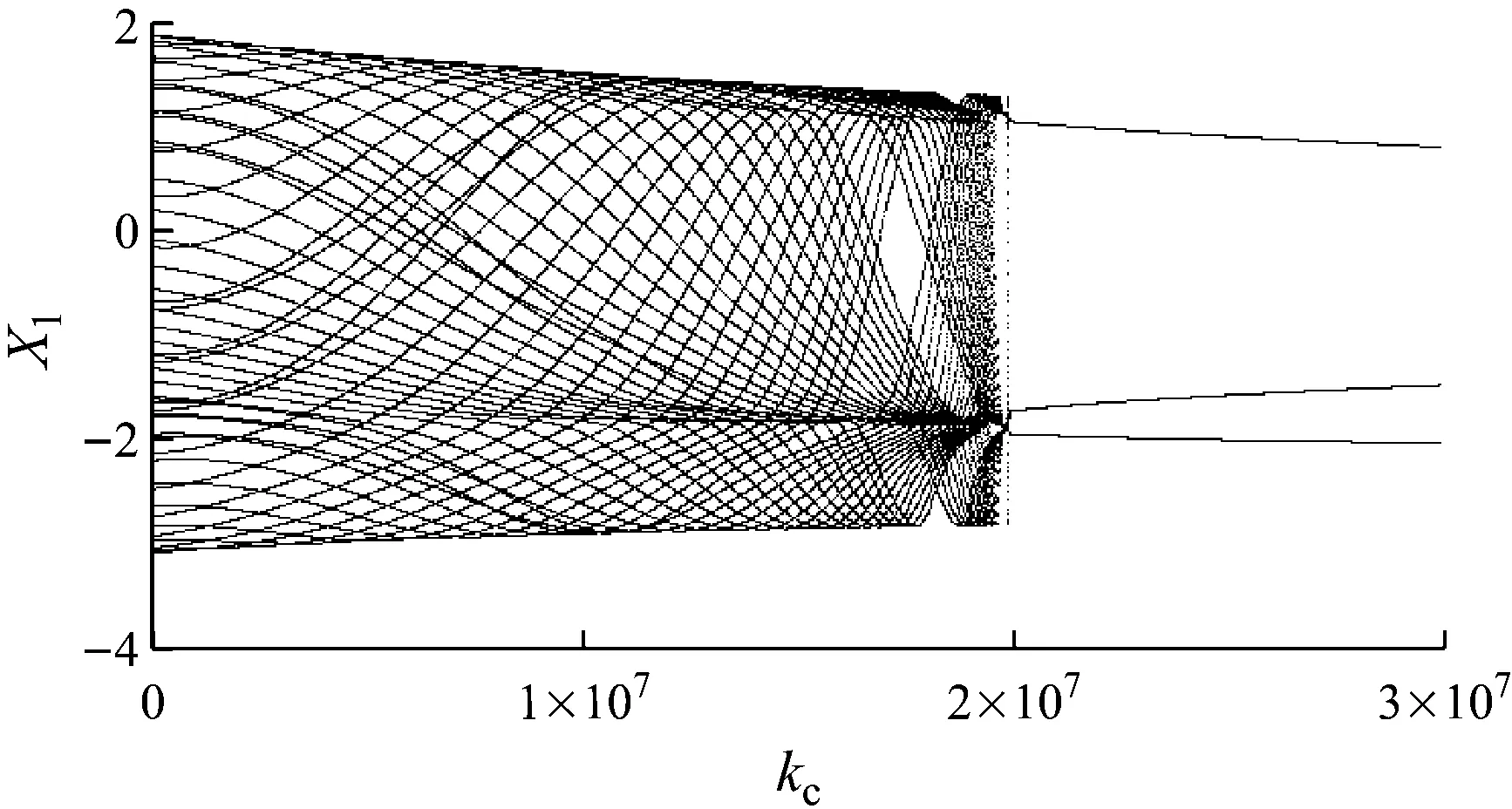
圖6 x方向位移響應隨碰摩剛度變化的分岔圖
Fig.6 Bifurcation diagram of displacement response inxdirection changing with rub-impact stiffness

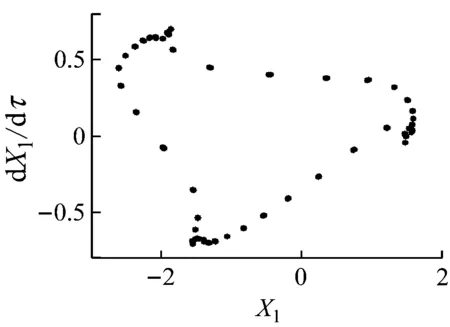
(a) kc=1.5×107 N/m(b) kc=2.5×107 N/m
圖7 不同碰摩剛度時的軸心軌跡圖和Poincaré圖
Fig.7 Axis trajectory diagrams and Poincaré maps at different rub-impact stiffness
3 結 論
(1)輪盤之間的非線性接觸對拉桿轉子軸承系統的響應產生較大影響,將拉桿轉子視為整體轉子進行分析將產生較大誤差.
(2)隨著輪盤轉速的變化,系統在非線性油膜力和碰摩力的作用下呈現出豐富的非線性特性,系統運動狀態在周期1、多周期、擬周期、混沌運動狀態之間轉變.
(3)碰摩剛度是影響系統運動狀態的一個重要因素,碰摩剛度的改變將引起系統運動狀態的改變.
[1] KHANLO H M, GHAYOUR M, ZIAEI-RAD S. The effects of lateral-torsional coupling on the nonlinear dynamic behavior of a rotating continuous flexible shaft-disk system with rub-impact[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(6): 1524-1538.
[2] 李朝峰, 周世華, 楊樹華, 等. 含有碰摩故障的多盤雙轉子系統動態特性[J]. 東北大學學報(自然科學版), 2014, 35(5): 726-730.
LI Chaofeng, ZHOU Shihua, YANG Shuhua, et al. Dynamic characteristics of stator-rotor interaction in multidisks dual-rotor system[J]. Journal of Northeastern University (Natural Science), 2014, 35(5): 726-730.
[3] 張婭, 王維民, 姚劍飛. 雙盤轉子系統軸向-徑向碰摩非線性動力學特性分析[J]. 振動與沖擊, 2012, 31(12): 141-145.
ZHANG Ya, WANG Weimin, YAO Jianfei. Nonlinear dynamic behavior of a double-disk isotropic rotor system with axial and radial rub-impacts[J]. Journal of Vibration and Shock, 2012, 31(12): 141-145.
[4] 向玲, 鄢小安. 汽輪機轉子故障診斷中LMD法和EMD法的性能對比研究[J]. 動力工程學報, 2014, 34(12): 945-951.
XIANG Ling, YAN Xiaoan. Performance contrast between LMD and EMD in fault diagnosis of turbine rotors[J]. Journal of Chinese Society of Power Engineering, 2014, 34(12): 945-951.
[5] 馬輝, 楊健, 宋溶澤, 等. 轉子系統碰摩故障實驗研究進展與展望[J]. 振動與沖擊, 2014, 33(6): 1-12.
MA Hui, YANG Jian, SONG Rongze, et al. Review and prospect on the research of rub-impact experiment of rotor systems[J]. Journal of Vibration and Shock, 2014, 33(6): 1-12.
[6] 姚紅良, 韓清凱, 李凌軒, 等. 基于諧波分量的轉子系統碰摩故障定量診斷方法[J]. 機械工程學報, 2012, 48(5): 43-48.
YAO Hongliang, HAN Qingkai, LI Lingxuan, et al. Method for detecting rubbing fault in rotor system based on harmonic components[J]. Journal of Mechanical Engineering, 2012, 48(5): 43-48.
[7] WANG J G, ZHOU J Z, DONG D W, et al. Nonlinear dynamic analysis of a rub-impact rotor supported by oil film bearings[J]. Archive of Applied Mechanics, 2013, 83(3): 413-430.
[8] ABU-MAHFOUZ I, BANERJEE A. On the investigation of nonlinear dynamics of a rotor with rub-impact using numerical analysis and evolutionary algorithms[J]. Procedia Computer Science, 2013, 20: 140-147.
[9] HEI D, LU Y J, ZHANG Y F, et al. Nonlinear dynamic behaviors of a rod fastening rotor supported by fixed-tilting pad journal bearings[J]. Chaos, Solitons & Fractals, 2014, 69: 129-150.
[10] HEI D, LU Y J, ZHANG Y F, et al. Nonlinear dynamic behaviors of rod fastening rotor-hydrodynamic journal bearing system[J]. Archive of Applied Mechanics, 2015, 85(7): 855-875.
[11] 程禮, 錢征文, 陳衛, 等. 結構參數對拉桿轉子雙穩態振動特性的影響[J]. 振動、測試與診斷, 2012, 32(5): 767-772.
CHENG Li, QIAN Zhengwen, CHEN Wei, et al. Influence of structural parameters on the bistable response of a disk-rod-fastening rotor[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 767-772.
[12] 錢征文, 程禮, 陳衛, 等. 盤式拉桿轉子雙穩態振動特性[J]. 航空動力學報, 2011, 26(7): 1563-1568.
QIAN Zhengwen, CHENG Li, CHEN Wei, et al. Analysis on bistable response of a disk-rod-fastening rotor[J]. Journal of Aerospace Power, 2011, 26(7): 1563-1568.
[13] CAPONE G. Analytical description of fluid-dynamic force field in cylindrical journal bearing[J]. L'Energia Elettrica, 1991, 68(3): 105-110.
Nonlinear Dynamic Response Characteristics of a Rod Fastening Rotor with Rub-Impact Faults
HULiang1,LIUYibing1,ZHAOLi1,2,ZHOUChao1
(1. Key Laboratory of Condition Monitoring and Control for Power Plant Equipment of Ministry of Education, North China Electric Power University, Beijing 102206, China;2. Beijing Energy Investment Holding Co., Ltd., Beijing 100022, China)
Nonlinear dynamic response characteristics of a rod fastening rotor with rub-impact faults at fixed points were studied. The specific way is to model the nonlinear contact characteristics between two disks as a spring with nonlinear bending stiffness, then to derive the motion equations of the rod fastening rotor bearing system based on D'Alembert principle considering nonlinear contact characteristics, linear oil film force and rub-impact force, and finally to solve above equations by numerical integration method, so as to analyze the variation law of the displacement response of system with the rotating speed and rub-impact stiffness of disks. Results show that the nonlinear contact between disks has a great influence on the displacement response of system; the system would exhibit strong nonlinear characteristics when the rotating speed of disk rises; the rub-impact force is a main factor affecting the motion state of the rod fastening rotor bearing system, and the motion state would change when the rub-impact force is increased.
rod fastening rotor; rub-impact; nonlinear dynamic; bifurcation; response characteristics; D'Alembert principle
2015-11-25
2016-10-03
北京市共建資助項目(ZDZH20141005401);中央高校基本科研業務費專項資金資助項目(2015XS79)
胡 亮(1988-),男,安徽淮南人,博士研究生,研究方向為旋轉機械動力學特性分析. 柳亦兵(通信作者),男,教授,博士生導師,電話(Tel.):010-61772252;E-mail:lyb@ncepu.edu.cn.
1674-7607(2017)07-0533-07
TH113
A
470.30

