基于離散狀態(tài)事件驅(qū)動(dòng)的電力電子瞬態(tài)過程仿真方法
檀 添 趙爭鳴 李帛洋 凌亞濤 陳凱楠
(清華大學(xué)電機(jī)系 電力系統(tǒng)及發(fā)電設(shè)備安全控制和仿真國家重點(diǎn)實(shí)驗(yàn)室 北京 100084)
基于離散狀態(tài)事件驅(qū)動(dòng)的電力電子瞬態(tài)過程仿真方法
檀 添 趙爭鳴 李帛洋 凌亞濤 陳凱楠
(清華大學(xué)電機(jī)系 電力系統(tǒng)及發(fā)電設(shè)備安全控制和仿真國家重點(diǎn)實(shí)驗(yàn)室 北京 100084)
為分析計(jì)算電力電子系統(tǒng)的電磁瞬態(tài)過程,需采用非理想開關(guān)器件模型,并計(jì)及電路中的雜散參數(shù)和控制回路中的時(shí)間延遲等,此時(shí)描述電力電子系統(tǒng)的數(shù)學(xué)模型呈現(xiàn)出高階非線性特性,且往往具有較強(qiáng)的剛性。采用常規(guī)微分方程的數(shù)值解算方法對(duì)于這種非線性的電力電子系統(tǒng)瞬態(tài)過程進(jìn)行仿真求解,存在仿真時(shí)間超長和數(shù)值穩(wěn)定性很差的問題。為解決這一問題,基于離散狀態(tài)事件驅(qū)動(dòng)(DSED)思想提出一類電力電子瞬態(tài)過程數(shù)值仿真方法,摒棄對(duì)時(shí)間離散的常規(guī)數(shù)值解算,而直接以狀態(tài)量的變化值作為仿真計(jì)算依據(jù)。理論推證和仿真解算比較結(jié)果表明:該方法能有效縮短解算時(shí)間,同時(shí)解決了常微分方程組的剛性問題,使得解算具有很好的數(shù)值穩(wěn)定性。
電力電子瞬態(tài)分析 離散狀態(tài)事件驅(qū)動(dòng) 仿真計(jì)算
0 引言
電力電子變換過程是一種利用弱電控制強(qiáng)電,實(shí)現(xiàn)電量變換的過程。在基于脈沖調(diào)制的電力電子變換系統(tǒng)中存在信號(hào)脈沖、驅(qū)動(dòng)脈沖、能量脈沖三種形式的脈沖序列[1]。其中,能量脈沖序列是電力電子系統(tǒng)實(shí)現(xiàn)電能變換的基本形式[2]。由于功率開關(guān)器件非理想因素[3,4]產(chǎn)生的死區(qū)[5]、最小脈寬[6]設(shè)置以及變換器線路雜散參數(shù)[7,8]的共同影響,變換器輸出的能量脈沖相對(duì)理想的信號(hào)脈沖存在延遲和畸變,這不僅對(duì)能量脈沖控制造成困難,產(chǎn)生“控制盲區(qū)”,甚至?xí)a(chǎn)生異常脈沖和破壞性脈沖[9],使系統(tǒng)或其中的器件發(fā)生失效或損壞,影響裝置的穩(wěn)定性和可靠性,而電力電子變換裝置中大部分失效發(fā)生在電磁瞬態(tài)過程中[9]。因此,進(jìn)行電力電子系統(tǒng)瞬態(tài)過程的仿真分析對(duì)提高控制精度、解決能量脈沖延遲畸變導(dǎo)致的電力電子裝置失效問題以及提高系統(tǒng)穩(wěn)定性和可靠性具有重要意義。
目前,常用的電力電子仿真軟件有Matlab、PSpice、PSIM等。文獻(xiàn)[10]列舉了各類電力電子仿真軟件的數(shù)值算法、開關(guān)器件模型及應(yīng)用特性等,其中關(guān)于上述三種仿真軟件的特性對(duì)比見表1[10]。

表1 Matlab、PSpice、PSIM的特性對(duì)比Tab.1 Feature comparison of Matlab, PSpice and PSIM
在電力電子系統(tǒng)瞬態(tài)分析中,由于系統(tǒng)復(fù)雜、存在耦合參數(shù)且各變量時(shí)間常數(shù)相差大[9],系統(tǒng)的狀態(tài)方程呈現(xiàn)出不連續(xù)點(diǎn)多、非線性和剛性強(qiáng)的特征,使用常規(guī)數(shù)值方法(如表1中的梯形法、R-K法等)不僅需要進(jìn)行迭代或插值以判定不連續(xù)點(diǎn),嚴(yán)重拖慢仿真速度,而且會(huì)面臨嚴(yán)重的數(shù)值不穩(wěn)定現(xiàn)象,算法收斂性差。使用變步長算法時(shí),為防止數(shù)值不穩(wěn)定現(xiàn)象發(fā)生,仿真步長將急劇縮小[11],從而導(dǎo)致超長的仿真時(shí)間,不滿足實(shí)際運(yùn)用的需要。為解決剛性系統(tǒng)仿真問題,Matlab自帶有剛性常微分方程組(Ordinary Differential Equation, ODE)數(shù)值解法[12],見表2。真的數(shù)值穩(wěn)定性問題,然而其單步計(jì)算量大和算法復(fù)雜的特性同樣導(dǎo)致仿真時(shí)間過長。

表2 Matlab中自帶的剛性常微分方程數(shù)值解法Tab.2 Numerical methods for stiff ODEs in Matlab
為解決上述問題,本文在電力電子系統(tǒng)瞬態(tài)分析中參照由Ernesto Kofman等提出的數(shù)值分析量化狀態(tài)系統(tǒng)(Quantized State System, QSS)算法[13-18],針對(duì)該算法的自身缺陷和電力電子系統(tǒng)仿真分析的實(shí)際需求應(yīng)用前文提出的基于離散狀態(tài)事件驅(qū)動(dòng)(Discrete State Event Driven, DSED)的電力電子系統(tǒng)瞬態(tài)過程仿真方法[19],且在原有QSS算法中加入導(dǎo)數(shù)限幅及所有狀態(tài)變量的導(dǎo)數(shù)線性化預(yù)估和校正,分別得到了DSED1和LIDSED1算法。最后以考慮非理想器件和線路雜散參數(shù)的三相兩電平逆變器為仿真對(duì)象,通過理論分析和算例應(yīng)用對(duì)比的方式論證了該方法在電力電子系統(tǒng)瞬態(tài)分析應(yīng)用中的有效性。
本文所有算例均使用處理器主頻3.6GHz計(jì)算機(jī)在Matlab平臺(tái)實(shí)現(xiàn)。
1 DSED方法在電力電子系統(tǒng)瞬態(tài)仿真中的實(shí)現(xiàn)
如引言中所述,使用DSED方法的主要目的是解決電力電子混雜系統(tǒng)數(shù)值仿真中的算法收斂性和速度問題,其核心是狀態(tài)離散和事件驅(qū)動(dòng)。下面首先介紹DSED方法在電力電子系統(tǒng)仿真中的實(shí)現(xiàn)步驟。
1)進(jìn)行系統(tǒng)參數(shù)的求取,并根據(jù)系統(tǒng)參數(shù)列寫系統(tǒng)狀態(tài)方程。
第k-1步計(jì)算得到系統(tǒng)所有狀態(tài)變量xi的Q函數(shù)Q(k-1)(x)構(gòu)成向量Q(k-1),x(change)為第k-1i步計(jì)算中唯一改變的狀態(tài)變量,其Q函數(shù)為Q(k-1)(x(change)),其中
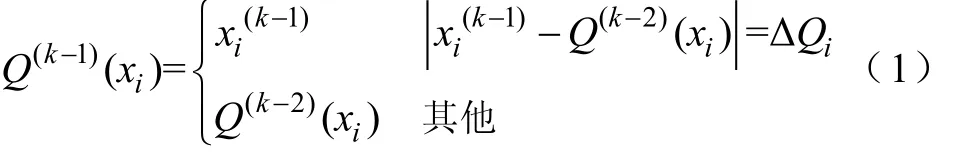
式中,ΔiQ為xi的量化長度,第k步計(jì)算中系統(tǒng)所有輸入ui(k)構(gòu)成向量U(k),和第k-1步比較發(fā)生變化的輸入構(gòu)成向量U(k)(change),則Q(k-1)(x(change))和U(k)(change)構(gòu)成第k步計(jì)算中的“事件”,用“event(k)”表示為
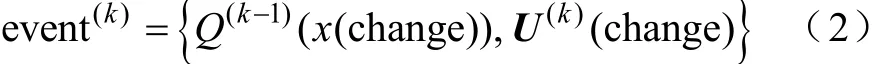
則第k步計(jì)算中系統(tǒng)所有參數(shù)值c(k)構(gòu)成的向量iC(k)由此步事件決定,即得到各參數(shù)值后根據(jù)模型特征和基爾霍夫定律列寫第k步計(jì)算的系統(tǒng)狀態(tài)方程為式中,矩陣A(k)(C(k))、B(k)(C(k))均由C(k)決定,x、x˙分別為所有狀態(tài)變量、所有狀態(tài)變量的導(dǎo)數(shù)構(gòu)成的向量;u為系統(tǒng)輸入。
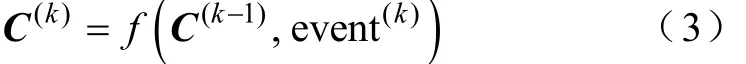
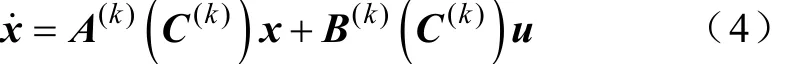
2)使用基于量化狀態(tài)系統(tǒng)的數(shù)值計(jì)算方法進(jìn)一步進(jìn)行數(shù)值ODE計(jì)算。
計(jì)算輸入Q(k-1)、x(k)決定該步狀態(tài)方程的矩陣A(k)(C(k))與B(k)(C(k))以及第k-1步計(jì)算結(jié)束時(shí)刻t(k-1),輸出為第k步計(jì)算得到的系統(tǒng)所有狀態(tài)變量xi的Q函數(shù)Q(k)(xi)構(gòu)成的向量Q(k)、所有狀態(tài)變量構(gòu)成的向量x(k)和第k步計(jì)算結(jié)束時(shí)刻t(k)。
3)判斷t(k)和設(shè)定的仿真終止時(shí)刻T的大小關(guān)系,若t(k)<T則繼續(xù)進(jìn)行第k+1步運(yùn)算,若t(k)≥T,則終止仿真,輸出仿真結(jié)果。
DSED方法在電力電子系統(tǒng)仿真中的使用流程如圖1所示。
從上述實(shí)現(xiàn)步驟中可以看到,DSED方法在電力電子系統(tǒng)仿真中具有如下優(yōu)勢:
(1)算法簡單。求解數(shù)值ODE方程組使用的量化狀態(tài)系統(tǒng)算法為顯式算法,且不存在任何迭代,相對(duì)傳統(tǒng)變步長剛性算法程序?qū)崿F(xiàn)較為容易,單步計(jì)算量小。
(2)仿真速度快。DSED方法固有的變步長性質(zhì)和較小的單步計(jì)算量使其相對(duì)傳統(tǒng)數(shù)值算法具有速度優(yōu)勢;同時(shí),由于采用量化狀態(tài)系統(tǒng)的思想,每步計(jì)算僅改變一個(gè)狀態(tài)變量Q函數(shù),所以每步計(jì)算在確定模型參數(shù)時(shí),僅僅需要重新計(jì)算與上一步計(jì)算唯一改變Q函數(shù)的狀態(tài)變量和該步計(jì)算改變的輸入值有關(guān)的參數(shù),相對(duì)傳統(tǒng)仿真方法減少了計(jì)算參數(shù)時(shí)的判斷和計(jì)算次數(shù),這也使仿真速度得到提升。
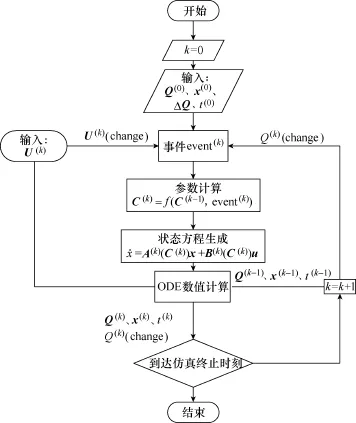
圖1 DSED的實(shí)現(xiàn)流程Fig.1 The implementation process of DSED
2 典型電力電子瞬態(tài)模型構(gòu)建與分析
選擇適合的非理想開關(guān)器件(IGBT、二極管)模型搭建一種典型的電力電子瞬態(tài)模型——帶阻感星形負(fù)載的三相兩電平逆變電路,用于對(duì)仿真算法的實(shí)現(xiàn)、驗(yàn)證和比較。
2.1 非理想開關(guān)器件模型
絕緣柵雙極型晶體管(Insulated Gate Bipolar Translator, IGBT)的模型選用文獻(xiàn)[5]所描述的一種高壓IGBT模型,該模型對(duì)IGBT的導(dǎo)通和關(guān)斷瞬態(tài)進(jìn)行了分段化處理,根據(jù)IGBT的開關(guān)特性將其開通、關(guān)斷瞬態(tài)過程各分為5個(gè)階段,從而近似得出IGBT的導(dǎo)通、關(guān)斷電壓和電流波形。在實(shí)際仿真過程中,該模型將IGBT等效為如圖2所示的電路,在導(dǎo)通和關(guān)斷的不同階段,改變參數(shù)Rg、Cgc、RPN以及IT的表達(dá)式。
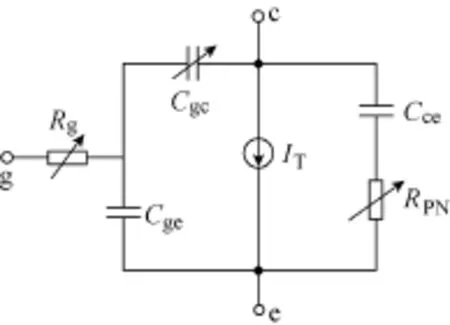
圖2 IGBT模型等效電路Fig.2 The equivalent circuit of IGBT model
圖2的等效電路中電流IT的表達(dá)式為
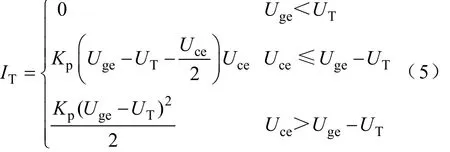
式中,UT為IGBT的閾值電壓;Uce、Uge分別為IGBT的ce極間電壓和ge極間電壓;Kp為比例系數(shù)。
圖2和式(5)中各參數(shù)值見表3。其中,Rgon、Rgoff分別為IGBT導(dǎo)通、關(guān)斷過程中的基區(qū)電阻;Cgc1為IGBT關(guān)斷第1階段和開通第5階段的gc極間電容,Cgc2為IGBT開通和關(guān)斷的其他階段中的gc極間電容;RPN1為IGBT開通和關(guān)斷的其他階段中基區(qū)電阻,RPN2為IGBT關(guān)斷第5階段和開通第1階段的基區(qū)電阻。
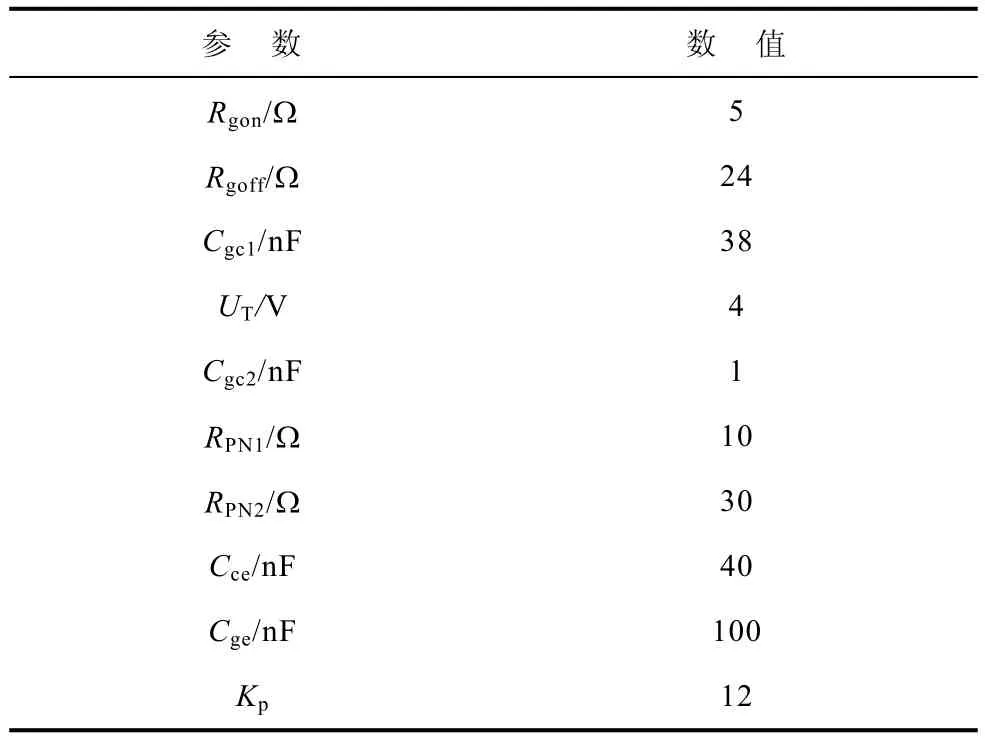
表3 IGBT模型等效電路中各參數(shù)值Tab.3 The parameters of equivalent circuit of IGBT model
二極管采用如圖3所示的等效電路模型。
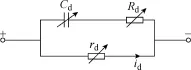
圖3 二極管模型等效電路Fig.3 The equivalent circuit of diode model
二極管建模基本思路是將其等效為1個(gè)理想二極管,并聯(lián)可變RC從而模擬其正、反向恢復(fù)特性[20],在圖3的等效電路中則由可變電阻Rd、可變電容Cd表示,兩者在二極管導(dǎo)通、截止瞬態(tài)時(shí)的取值分別為Rdon、Rdoff和Cdon、Cdoff。為了模型建立的方便,模擬二極管穩(wěn)態(tài)時(shí)期的漏電流、管壓降,將理想二極管部分用另一個(gè)可變電阻rd代替。當(dāng)通過理想二極管部分的電流id>0時(shí),二極管看作導(dǎo)通,rd取小電阻值rdon;當(dāng)通過理想二極管部分的電流id<0時(shí),二極管看作截止,rd取大電阻值rdoff。二極管模型等效電路中各參數(shù)值見表4。2.2 三相兩電平逆變器系統(tǒng)模型

表4 二極管模型等效電路中各參數(shù)值Tab.4 The parameters of equivalent circuit of diode model
主仿真電路拓?fù)淙鐖D4所示。圖中,LS1+、LS2+、LS3+、LS1-、LS2-、LS3-為母排雜散電感。為簡化模型,設(shè)其值均相等,用LS表示。US為直流電壓源電壓,RA、RB、RC分別為三相負(fù)載電阻,LA、LB、LC分別為三相負(fù)載電感。由于負(fù)載為三相對(duì)稱負(fù)載,所以三相的電阻電感值分別相等,表示為R、L。仿真中,取LS=0.8μH ,US=300V ,R=1mΩ,L=10mH。除此之外,所有IGBT及其反并聯(lián)二極管的等效電路參數(shù)都相同。
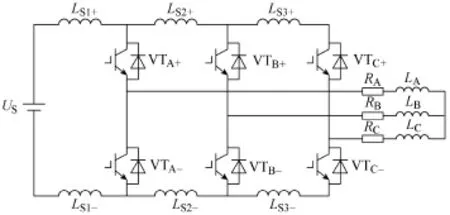
圖4 主仿真電路拓?fù)銯ig.4 Topology of main circuit for simulation
本文分析的是IGBT的開關(guān)瞬態(tài)過程,而負(fù)載電感值相對(duì)雜散參數(shù)較大,所以可認(rèn)為在瞬態(tài)過程中負(fù)載電流不會(huì)改變方向。據(jù)此可以對(duì)圖4的拓?fù)溥M(jìn)行簡化,只保留負(fù)載電流通過的換流電路。當(dāng)負(fù)載電流方向如圖5中所示時(shí)(A、B相電流流入橋臂,C相電流流出橋臂),換流通路為A、B相橋臂上管IGBT、下管反并聯(lián)二極管以及C相橋臂上管的反并聯(lián)二極管、下管IGBT。整個(gè)仿真模型如圖5所示。
對(duì)圖5所示拓?fù)溥M(jìn)行電路分析后可以得到的系統(tǒng)狀態(tài)方程為
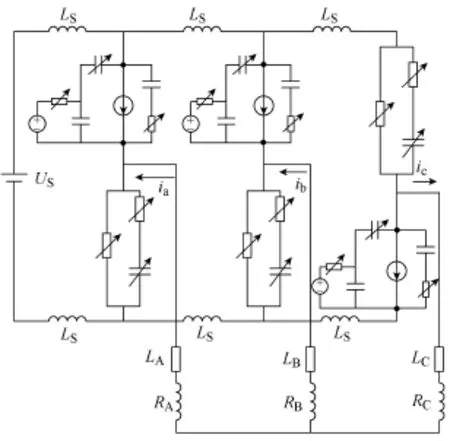
圖5 簡化后的仿真模型Fig.5 Simulation model after simplification

式中,x˙為17個(gè)狀態(tài)變量導(dǎo)數(shù)組成的向量;x為17個(gè)狀態(tài)變量組成的向量,狀態(tài)變量選取為模型中各電容電壓和電感電流;u為7個(gè)輸入變量構(gòu)成的向量,輸入變量選取為4個(gè)電壓源電壓(電源電壓US和圖4中各IGBT柵極電壓)以及圖4中各IGBT的電流IT等效電流源電流;系數(shù)矩陣A17×17∈R,Β17×7∈R,兩者在IGBT瞬態(tài)過程經(jīng)歷的各個(gè)階段內(nèi)部為常系數(shù)矩陣,跨越階段時(shí)系數(shù)發(fā)生改變。
2.3 系統(tǒng)剛性分析
取2.2節(jié)所述瞬態(tài)模型在實(shí)際仿真中容易出現(xiàn)剛性振蕩的一個(gè)瞬態(tài)階段,即VTA+管處于關(guān)斷穩(wěn)態(tài),VTB+管處于開通最后階段,VTC+管處于開通穩(wěn)態(tài)。受線路雜散電感影響,VTB+管出現(xiàn)短時(shí)反并聯(lián)二極管續(xù)流的現(xiàn)象,等效于在VTB+管c、e極間并接小電阻,系統(tǒng)剛性大大增加。設(shè)λi為A的特征值(i=1,2,…,17),計(jì)算各λi值可知其滿足關(guān)系為
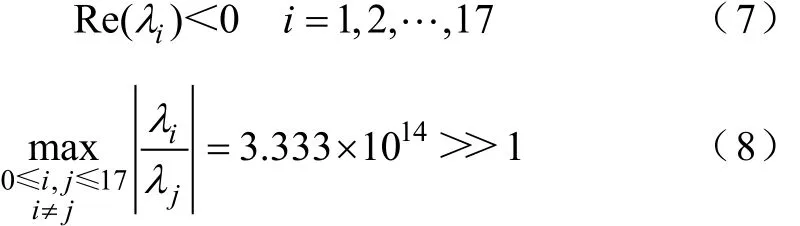
式(7)和式(8)表明,該狀態(tài)下系統(tǒng)狀態(tài)方程為剛性常微分方程[20],且會(huì)發(fā)生剛性振蕩[21]。
取h為時(shí)間步長。由于電力電子開關(guān)瞬態(tài)過程時(shí)間尺度為μs級(jí)[9],為保證一定的計(jì)算準(zhǔn)確性,h至少需要再小1個(gè)數(shù)量級(jí),此時(shí)可忽略h的高階成分。此情況下容易推導(dǎo),對(duì)于式(6)所示常微分方程的解算,常用的三種顯式方法向前Euler、PECE Euler和4階R-K法的數(shù)值穩(wěn)定性條件分別為
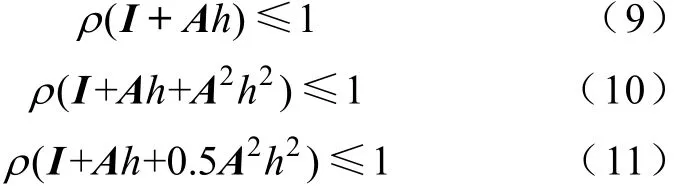
式中,I為單位矩陣;()ρ?為求取矩陣的譜半徑函數(shù)。
進(jìn)一步忽略h的高階成分,式(10)和式(11)均可轉(zhuǎn)化為式(9)。解不等式,得

按此步長,即使是解算5μs的瞬態(tài)過程也至少需要8.5×107步,在Matlab平臺(tái)中使用CPU主頻3.6GHz的計(jì)算機(jī)(下文仿真計(jì)算均使用此平臺(tái)和計(jì)算機(jī))運(yùn)算至少需要113.4s。所以使用顯式方法時(shí),所取步長需遠(yuǎn)小于所需仿真精度,且?guī)磉^長的仿真時(shí)間。
各種隱式剛性算法的使用可以克服上述問題,然而算法復(fù)雜度大大增加,各步均存在迭代,單步計(jì)算量大,仿真速度同樣難以滿足要求。
下面使用引言部分介紹的Matlab中自帶剛性算法對(duì)該瞬態(tài)模型進(jìn)行分析。分析過程為:1個(gè)開關(guān)周期中,VTA+管處于關(guān)斷穩(wěn)態(tài),VTC+管處于開通穩(wěn)態(tài),VTB+管在1個(gè)周期內(nèi),經(jīng)歷關(guān)斷、開通兩個(gè)過程,其開關(guān)周期為0.2ms,占空比為50%。表5統(tǒng)計(jì)比較了四種算法仿真性能,可見,相對(duì)誤差設(shè)置相同時(shí),具有二階向后微分公式的梯形法(Trapezoidal Rule with the Second Order Backward Difference Formula, TR-BDF2)(命令為“ode23tb”)仿真速度最快,故本文將用其與DSED方法的仿真性能進(jìn)行對(duì)比。
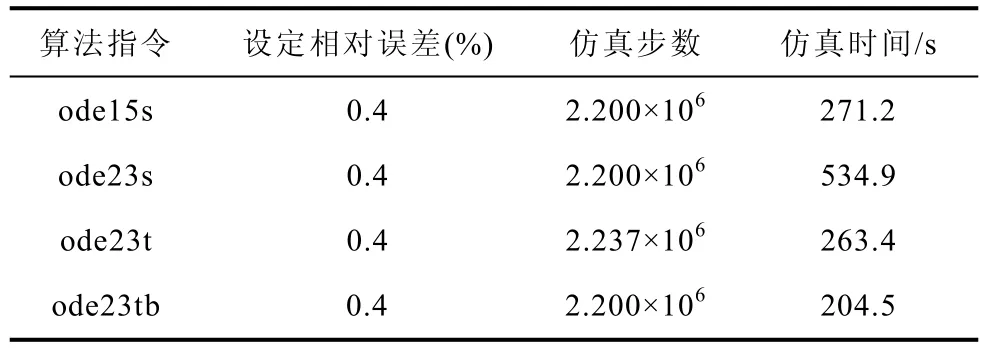
表5 電力電子瞬態(tài)仿真中各剛性算法仿真性能Tab.5 Performance of algorithms for stiff ODEs on transient simulation of power electronic converters
3 DSED方法的改進(jìn)方法
3.1 DSED方法在電力電子瞬態(tài)仿真中的局限性
文獻(xiàn)[13]指出,在使用QSS算法進(jìn)行系統(tǒng)仿真分析時(shí),量化長度ΔQ的選取對(duì)仿真精度和速度都有決定性影響。本文將通過算例分析研究ΔQ對(duì)DSED方法仿真性能的影響。為運(yùn)算精確而穩(wěn)定地進(jìn)行,各狀態(tài)變量的量化長度大小與其穩(wěn)態(tài)下幅值須成等比例關(guān)系[18],設(shè)k為比例系數(shù),即
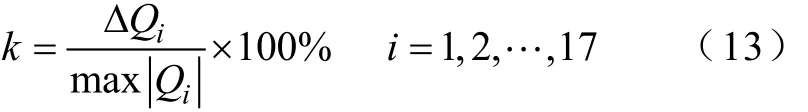
取k=0.4%,用DSED方法對(duì)第2節(jié)所述的開關(guān)周期進(jìn)行仿真。仿真總步數(shù)為76.06110×,用時(shí)644.5s。其中,2.3節(jié)所分析剛性最強(qiáng)階段的仿真時(shí)間占用了總仿真時(shí)間的99.68%。圖6分別展示了使用DSED法和相對(duì)誤差為0.4%的TR-BDF2法(Matlab命令為“ode23tb”)所得此過程中VTB+管動(dòng)作時(shí)的管壓降和電流波形。
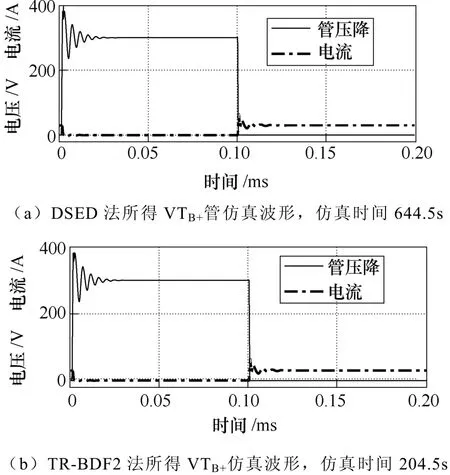
圖6 使用DSED和TR-BDF2法的仿真波形Fig.6 Simulation waveforms calculated by DSED and TR-BDF2
對(duì)比圖6a和圖6b的仿真波形可發(fā)現(xiàn),使用DSED方法會(huì)導(dǎo)致穩(wěn)態(tài)過程中仿真波形出現(xiàn)幅值較大的低頻數(shù)值振蕩。同時(shí),在剛性較強(qiáng)的區(qū)域,仿真波形會(huì)出現(xiàn)頻率極高、幅值較小的高頻數(shù)值振蕩。低頻振蕩和高頻振蕩的放大波形如圖7所示。
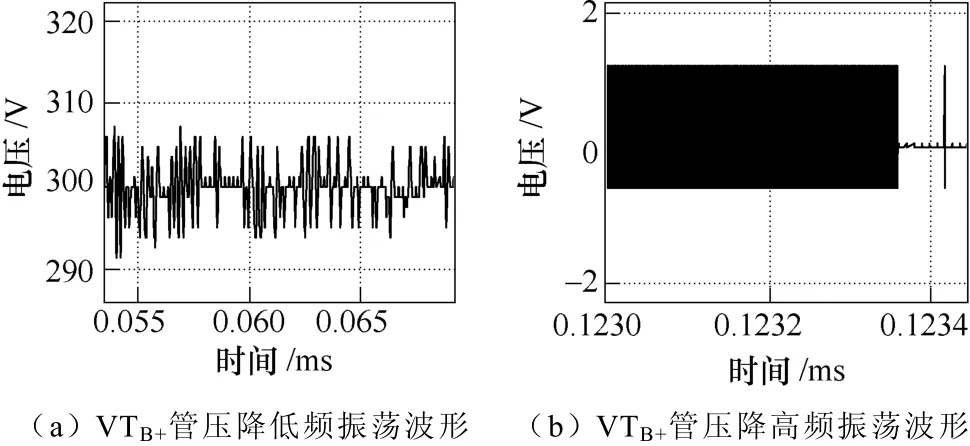
圖7 使用DSED方法時(shí)的振蕩放大波形Fig.7 Oscillating waveforms calculated by DESE
圖7中,低頻振蕩雖然幅值較高,會(huì)造成仿真準(zhǔn)確性的降低,然而其振蕩頻率較低,對(duì)仿真速度影響較小,在對(duì)精度要求較低的場合這種低頻振蕩是可以接受的。強(qiáng)剛性階段的高頻振蕩由于其振蕩頻率特別高,相應(yīng)會(huì)在該階段造成極大的仿真步數(shù)和仿真時(shí)間,這便是在剛性最強(qiáng)階段的仿真時(shí)間占用了總仿真時(shí)間99.68%的原因。高頻振蕩的存在導(dǎo)致DSED方法相對(duì)傳統(tǒng)剛性算法(TR-BDF2法)不存在任何速度優(yōu)勢,反而在仿真精度上存在劣勢。消除DSED方法仿真中的高頻振蕩成為其能夠在電力電子瞬態(tài)仿真中取得應(yīng)用的關(guān)鍵。
3.2 抑制高頻振蕩的改進(jìn)DSED方法
振蕩的“高頻”直接來源于對(duì)應(yīng)每步計(jì)算中的“高導(dǎo)數(shù)”。在狀態(tài)變量量化長度固定的條件下,某狀態(tài)變量導(dǎo)數(shù)絕對(duì)值過大將直接導(dǎo)致該步計(jì)算時(shí)間間隔過小,如果這種狀態(tài)不斷重復(fù),宏觀上表現(xiàn)為高頻振蕩。基于此思想可使用在每步計(jì)算中對(duì)全局限制導(dǎo)數(shù)幅值來抑制高頻振蕩。
全局限制狀態(tài)變量導(dǎo)數(shù)幅值的原則是:在有效抑制高頻振蕩的同時(shí)保證不破壞計(jì)算的準(zhǔn)確性。一般使用“嘗試法”確定為抑制高頻振蕩所設(shè)導(dǎo)數(shù)絕對(duì)值上界,也可以通過估算系統(tǒng)“正常”導(dǎo)數(shù)值的范圍來確定導(dǎo)數(shù)限幅上界。在本文分析的電力電子瞬態(tài)模型中,狀態(tài)變量的導(dǎo)數(shù)主要來源于電感和電容元件,其估算表達(dá)式分別為

式中,i、u為狀態(tài)變量,分別表示流過電感的電流和電容兩端的電壓;L、C分別為電感、電容值;uL、iC分別為電感兩端電壓和流過電容的電流。
以本文仿真系統(tǒng)為例,系統(tǒng)中包含最小電容和電感分別為1nF、0.8μH,整個(gè)系統(tǒng)電容電壓、電感電流的穩(wěn)態(tài)峰值分別約為385V、66A。由式(14)和式(15)可得電流、電壓的導(dǎo)數(shù)最大值分別為
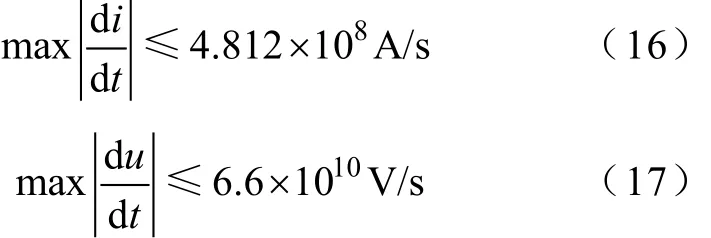
為確保導(dǎo)數(shù)限幅不對(duì)系統(tǒng)變化造成影響,取導(dǎo)數(shù)絕對(duì)值上界比“正常”導(dǎo)數(shù)的最大值還大1個(gè)數(shù)量級(jí),即令

在DSED方法中加入式(18)所示限幅條件,則在進(jìn)行2.3節(jié)所述瞬態(tài)仿真中,總仿真步數(shù)由傳統(tǒng)DSED方法的6.061×107步縮減為5.877×105步,而仿真波形除了消除高頻振蕩外沒有任何改變。
事實(shí)上,式(18)給出的是考慮最壞情況,同時(shí)放了一個(gè)數(shù)量級(jí)余量的理論限幅條件。利用“嘗試法”在實(shí)際仿真中,只需將導(dǎo)數(shù)幅值上限定為1010,便可保證其不影響正常的仿真波形。這種情況下,總仿真步數(shù)進(jìn)一步縮減為1.357×105步,相當(dāng)于將仿真速度又提高了4倍多,仿真時(shí)間為1.354s,相對(duì)DSED方法仿真速度提高400倍。在不考慮精度的情況下相對(duì)TR-BDF2法仿真速度提升兩個(gè)數(shù)量級(jí)。
3.3 抑制低頻振蕩幅值的改進(jìn)LIDSED算法
文獻(xiàn)[15,16]介紹了針對(duì)顯式QSS方法振蕩問題的隱式線性量化狀態(tài)空間方法(LIQSS法),并給出LIQSS1法(1階)相應(yīng)顯式算法。該算法基本思路是:由于QSS方法中,每步運(yùn)算僅僅改變1個(gè)狀態(tài)變量的Q函數(shù)。故在第k步計(jì)算中,首先對(duì)k-1步計(jì)算中唯一Q函數(shù)發(fā)生變化的狀態(tài)變量(假定為ix)的Q函數(shù)iq以及導(dǎo)數(shù)ix˙進(jìn)行線性化預(yù)估,即
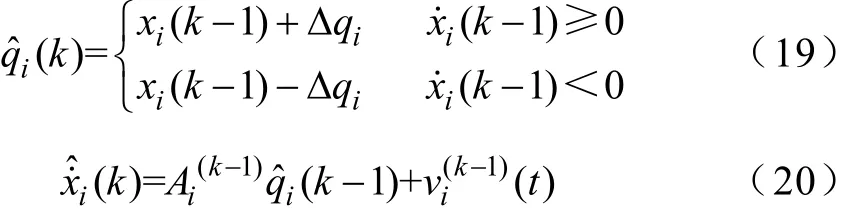
式中,Δqi為xi的量化長度;Ai、vi(t)分別為導(dǎo)數(shù)預(yù)估線性方程的系數(shù),確定方法為
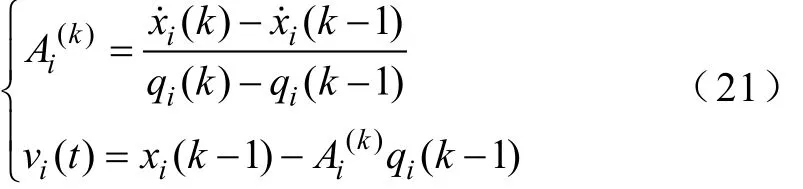
接下來用預(yù)估的ix˙校正iq,再將iq以及其余狀態(tài)變量Q函數(shù)代入狀態(tài)方程校正ix˙。其余步驟與QSS1法相同。
這種算法由于每步運(yùn)算實(shí)際上僅僅對(duì)1個(gè)狀態(tài)變量進(jìn)行預(yù)估校正處理,對(duì)振蕩的抑制極為有限。在本文分析的仿真系統(tǒng)中,狀態(tài)變量共17個(gè),如果用此算法效果幾乎與QSS1法沒有區(qū)別。針對(duì)這個(gè)問題,本文提出一種適用于電力電子仿真,對(duì)所有狀態(tài)變量進(jìn)行線性化預(yù)估校正的改進(jìn)LIDSED方法。仍然假定k-1步計(jì)算中唯一Q函數(shù)發(fā)生變化的狀態(tài)變量為ix。任取117j≤≤,則狀態(tài)變量xj的Q函數(shù)qj以及導(dǎo)數(shù)值jx˙的線性化預(yù)估過程改進(jìn)為
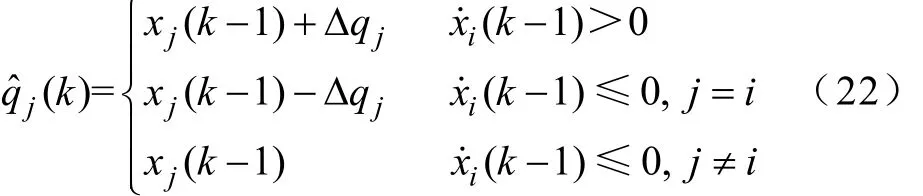
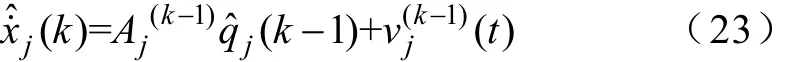
其余步驟不作改變(也加入了導(dǎo)數(shù)限幅)。取k值同為0.4%,比較改進(jìn)QSS1法和改進(jìn)LIQSS1法得到的VTB+管仿真波形,如圖8所示。
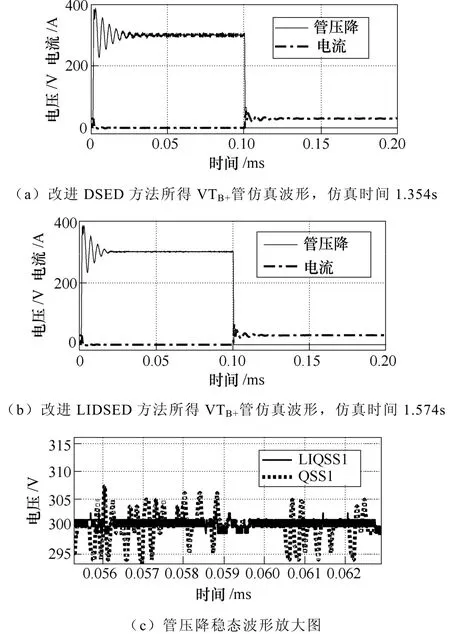
圖8 同量化長度ΔQ下改進(jìn)DSED方法和改進(jìn)LIDSED方法的仿真波形Fig.8 Simulation waveforms calculated by modified DSED and LIDSED with same ΔQ
由圖8可知,等量化長度下,使用LIDSED方法可以有效抑制低頻振蕩幅值,從而提升仿真的精度。此外,由于其單步計(jì)算量相對(duì)上述導(dǎo)數(shù)限幅的DSED方法大,所以仿真時(shí)間有輕微增加。
4 DSED方法的仿真性能分析
基于表5所示結(jié)果,在本文電力電子仿真模型和仿真階段中使用Matlab自帶剛性算法等相對(duì)誤差情況下,仿真速度最快的TR-BDF2法和本文提出的改進(jìn)DSED方法、改進(jìn)LIDSED方法進(jìn)行精度、速度性能的分析比較。
仿真速度可由仿真時(shí)間表示,仿真精度的表示方法是:改進(jìn)DSED方法所得VTB+管壓降數(shù)據(jù)和TR-BDF2法所得VTB+管壓降數(shù)據(jù)分別進(jìn)行2 000項(xiàng)線性插值后取兩者插值結(jié)果差的方均根。如果y、?y分別表示QSS方法和TR-BDF2法的插值結(jié)果,則方均根誤差RMSE為
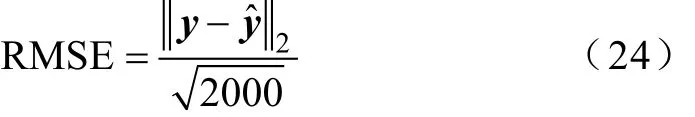
改變量化長度,得到改進(jìn)DSED法和改進(jìn)LIDSED法仿真速度和結(jié)果的方均根誤差如圖9所示。
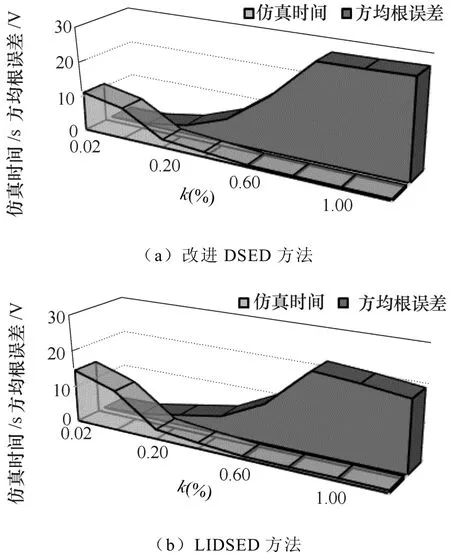
圖9 改進(jìn)DSED方法的仿真性能Fig.9 Simulation performance of modified DSED methods
圖9中,k定義如式(13)所示,為量化長度ΔQ的大小。由圖9可知,隨著ΔQ的增大,改進(jìn)DSED方法和LIDSED方法的仿真速度隨之提升,而兩者的仿真精度隨之下降。當(dāng)ΔQ增大到一定程度時(shí),繼續(xù)增加ΔQ,兩種方法的仿真速度和精度變化將不再明顯。因此,在實(shí)際仿真過程中,應(yīng)根據(jù)實(shí)際對(duì)仿真速度和精度的需要進(jìn)行ΔQ選取。
改進(jìn)的DSED方法和LIDSED方法仿真精度和ΔQ的關(guān)系如圖10所示。分析圖10不難發(fā)現(xiàn),在每一個(gè)相同ΔQ下,改進(jìn)LIDSED方法均相對(duì)改進(jìn)DSED方法具有精度優(yōu)勢,相對(duì)TR-BDF2法的方均根誤差較改進(jìn)QSS1法小,原因是其對(duì)仿真結(jié)果低頻振蕩幅值起到了一定抑制作用,這也驗(yàn)證了第3節(jié)的分析。
然而,在相同ΔQ下,改進(jìn)DSED方法仿真時(shí)間略高于改進(jìn)LIDSED方法,如圖11所示。所以在運(yùn)用中,兩者的選用也需要根據(jù)實(shí)際仿真需要和在仿真模型中兩種算法的速度和精度表現(xiàn)來作選擇。
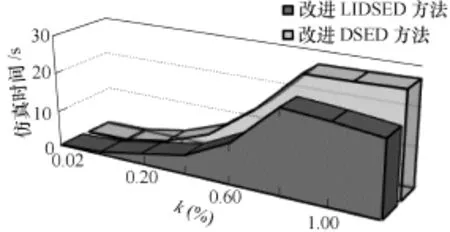
圖10 改進(jìn)DSED方法和LIDSED方法的仿真精度Fig.10 Simulation precision of modified DSED and LIDSED
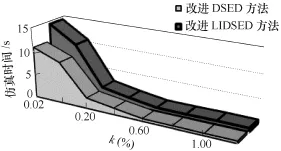
圖11 改進(jìn)DSED方法和LIDSED方法的仿真時(shí)間Fig.11 Simulation time of modified DSED and LIDSED
5 結(jié)論
本文將基于離散狀態(tài)事件驅(qū)動(dòng)(DSED)的數(shù)值仿真方法應(yīng)用于電力電子系統(tǒng)瞬態(tài)仿真,搭建了典型的電力電子瞬態(tài)仿真系統(tǒng)——考慮非理想開關(guān)器件和線路雜散參數(shù)的三相兩電平逆變電路。以此為分析對(duì)象,實(shí)現(xiàn)了DSED方法在電力電子瞬態(tài)仿真中的運(yùn)用,并根據(jù)文獻(xiàn)[13-19]所提出的QSS方法的局限性和仿真需要,提出了兩種改進(jìn)的DSED方法——改進(jìn)DSED方法和改進(jìn)LIDSED方法。并以第2節(jié)仿真系統(tǒng)為算例,分析了兩者的仿真性能,相互比較并與Matlab自帶剛性算法進(jìn)行對(duì)比。得到如下結(jié)論:
1)電力電子瞬態(tài)仿真系統(tǒng)(以本文使用系統(tǒng)為例)具有剛性強(qiáng)、不連續(xù)點(diǎn)多等特點(diǎn),傳統(tǒng)時(shí)間離散算法存在速度慢、收斂性差的特點(diǎn)。
2)在Matlab平臺(tái)實(shí)現(xiàn)了使用DSED方法代替?zhèn)鹘y(tǒng)時(shí)間離散方法進(jìn)行電力電子系統(tǒng)瞬態(tài)仿真。
3)針對(duì)DSED方法中高頻振蕩問題,基于DSED方法提出基于導(dǎo)數(shù)限幅的改進(jìn)DSED方法,有效抑制高頻振蕩,相對(duì)傳統(tǒng)時(shí)間離散剛性算法將仿真速度提升兩個(gè)數(shù)量級(jí)。
4)針對(duì)改進(jìn)DSED方法存在較大幅值低頻振蕩現(xiàn)象,基于LIQSS1方法提出改進(jìn)LIDSED方法,相對(duì)改進(jìn)DSED方法能有效削弱低頻振蕩幅值,提高仿真精度。
5)改進(jìn)DSED方法和LIDSED方法的仿真速度隨量化長度ΔQ增加而升高,仿真精度隨量化長度ΔQ增加而降低,且兩者的變化趨勢在ΔQ增加到一定程度時(shí)均呈現(xiàn)“飽和”特征。
6)盡管ΔQ相同時(shí)改進(jìn)LIDSED方法仿真精度高于改進(jìn)DSED方法,然而其仿真速度卻相對(duì)較慢。具體使用時(shí)需根據(jù)實(shí)際情況選擇適合的算法。
通過算法比較和算例分析,總結(jié)DSED仿真方法有待解決的問題和進(jìn)一步發(fā)展方向。
1)DSED方法進(jìn)行電力電子系統(tǒng)仿真時(shí),需要列寫電路狀態(tài)方程。為提升算法實(shí)用性,需要在DSED方法中加入自動(dòng)識(shí)別電力電子系統(tǒng)開關(guān)過程以及根據(jù)電路拓?fù)浜退帬顟B(tài)自動(dòng)列寫狀態(tài)方程的相關(guān)算法。
2)改進(jìn)DSED方法中,導(dǎo)數(shù)限幅過程依賴于模型的特性(電感、電容和狀態(tài)變量峰值)。如需進(jìn)一步提升算法性能,需要找到自適應(yīng)的導(dǎo)數(shù)限幅方式或開發(fā)隱式DSED方法。
[1] 魯挺. 大容量電力電子系統(tǒng)非理想功率脈沖特性及其控制方法[D]. 北京: 清華大學(xué), 2010.
[2] 趙爭鳴, 賀凡波, 袁立強(qiáng), 等. 大容量電力電子系統(tǒng)電磁瞬態(tài)分析技術(shù)及應(yīng)用[J]. 中國電機(jī)工程學(xué)報(bào), 2014, 34(18): 3013-3019. Zhao Zhengming, He Fanbo, Yuan Liqiang, et al. Techniques and applications of electromagnetic transient analysis in high power electronic systems[J]. Proceedings of the CSEE, 2014, 34(18): 3013-3019.
[3] Ji S, Lu T, Zhao Z, et al. Modelling of high voltage IGBT with easy parameter extraction[C]//IEEE Power Electronics and Motion Control Conference, Harbin, China, 2012: 1511-1515.
[4] Ji S, Zhao Z, Yuan L. HVIGBT physical model analysis during transient[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2616-2624.
[5] 劉軍鋒, 李葉松. 死區(qū)對(duì)電壓型逆變器輸出誤差的影響及其補(bǔ)償[J]. 電工技術(shù)學(xué)報(bào), 2007, 22(5):117-122. Liu Junfeng, Li Yesong. Dead-time influence on output error of voltage source inverter and compensation[J]. Transactions of China Electrotechnical Society, 2007, 22(5): 117-122.
[6] 白華, 趙爭鳴, 張永昌, 等. 最小脈寬特性對(duì)高壓三電平變頻器的影響[J]. 電工技術(shù)學(xué)報(bào), 2006, 21(12): 60-65. Bai Hua, Zhao Zhengming, Zhang Yongchang, et al. Effect of minimum pulse width on high voltage three-level inverters[J]. Transactions of China Electrotechnical Society, 2006, 21(12): 60-65.
[7] 李锃. 大功率多電平逆變器寄生參數(shù)對(duì)電路性能影響和抑制的分析與研究[D]. 杭州: 浙江大學(xué), 2008.
[8] 于華龍, 趙爭鳴, 袁立強(qiáng), 等. 高壓IGBT串聯(lián)變換器直流母排設(shè)計(jì)與雜散參數(shù)分析[J]. 清華大學(xué)學(xué)報(bào): 自然科學(xué)版, 2014, 54(4): 540-545. Yu Hualong, Zhao Zhengming, Yuan Liqiang, et al. High-voltage IGBTs series converter bus bar design and stray parameter analysis[J]. Journal of Tsinghua University: Science and Technology, 2014, 54(4):540-545.
[9] 趙爭鳴, 白華, 袁立強(qiáng). 電力電子學(xué)中的脈沖功率瞬態(tài)過程及其序列[J]. 中國科學(xué): 技術(shù)科學(xué), 2007, 37(1): 60-69. Zhao Zhengming, Bai Hua, Yuan Liqiang. Transient process and sequence of power pulse in power electronics[J]. Science China Technological Sciences, 2007, 37(1): 60-69.
[10] 陳建業(yè). 電力電子電路的計(jì)算機(jī)仿真[M]. 北京:清華大學(xué)出版社, 2008.
[11] Hairer E, Wanner G. Solving ordinary differential equations II: stiff and differential-algebraic problems[J]. Springer Series in Computational Mathematics, 1996, 8(3): 611-614.
[12] Shampine L F, Reichelt M W. The MATLAB ODE Suite[J]. Siam Journal on Scientific Computing, 1997, 18(1): 1-22.
[13] Cellier F E, Kofman E. Continuous system simulation[M]. New York, US: Springer, 2010.
[14] Migoni G, Kofman E, Cellier F. Quantization-based new integration methods for stiff ordinary differential equations[J]. Simulation Modelling Practice & Theory, 2012, 35(4): 387-407.
[15] Migoni, Kofman G E. Linearly implicit discrete event methods for stiff ODE's[J]. Latin American Applied Research Pesquisa Aplicada Latino Americana Investigación Aplicada Latinoamericana, 2009, 39(39): 245-254.
[16] Migoni G, Bortolotto M, Kofman E, et al. Linearly implicit quantization-based integration methods for stiff ordinary differential equations[J]. Simulation Modelling Practice & Theory, 2013, 35(6): 118-136.
[17] Migoni G, Kofman E, Bergero F, et al. Quantizationbased simulation of switched mode power supplies[J]. Simulation Transactions of the Society for Modeling & Simulation International, 2015, 91(4): 320-336.
[18] Song X, Ma Y, Zhang W, et al. Quantized state based simulation of time invariant and time varying continuous systems[J]. Mathematical Problems in Engineering, 2015, 2015: 1-5.
[19] 袁立強(qiáng), 趙爭鳴, 宋高升, 等. 電力半導(dǎo)體器件原理與應(yīng)用[M]. 北京: 機(jī)械工業(yè)出版社, 2011.
[20] Brenan K E, Campbell S L, Petzold L R. Numerical solution of initial-value problems in differentialalgebraic equations[M]. New York: North-Holland, 1989.
[21] 費(fèi)景高. 微分代數(shù)方程的一類并行算法[J]. 計(jì)算機(jī)工程與科學(xué), 1992, 14(4): 55-68. Fei Jinggao. A class of parallel algorithms for differential algebraic equations[J]. Computer Engineering & Science, 1992, 14(4): 55-68.
(編輯 陳 誠)
Discrete State Event Driven Based Methods for Transient Simulation of Power Electronic Converters
Tan Tian Zhao Zhengming Li Boyang Lin Yatao Chen Kainan
(State Key Laboratory of Control and Simulation of Power Systems and Generation Equipments Department of Electrical Engineering Tsinghua University Beijing 100084 China)
In order to calculate electromagnetic transients of power electronic systems, non-ideal physical models considering stray parameters of circuits and time delay of control loops are needed for semiconductor switching device. In this case, the mathematical models describing power electronic system exhibit high-order nonlinearity and tend to be highly rigid. The numerical solution methods through the conventional differential equations shall bring about the problems of long simulation time and poor numerical stability. Thus, this paper puts forward the improved methods for transient simulation of power electronic converters based on discrete state event driven (DSED) methods. These methods use the variation of state variable as the calculation basis rather than the variation of simulation time. It is demonstrated the methods could reduce simulation time effectively and solve the stiff problem of ordinary differential equations, which ensure numerically stable of the simulation.
Transient simulation of power electronic converters, discrete state event driven, simulating calculation
TM46
檀 添 男,1995年生,博士研究生,研究方向?yàn)槭录?qū)動(dòng)的電力電子仿真方法。
E-mail: tantiantsinghua@sina.cn
趙爭鳴 男,1959年生,教授,博士生導(dǎo)師,研究方向?yàn)榇笕萘侩娏﹄娮幼儞Q系統(tǒng)、光伏發(fā)電、電機(jī)控制、無線電能傳輸?shù)取?/p>
E-mail: zhaozm@tsinghua.edu.cn(通信作者)
10.19595/j.cnki.1000-6753.tces.170341
國家自然科學(xué)基金重大項(xiàng)目資助(51490680,51490683)。
2017-02-06 改稿日期 2017-03-29

