一種聚類優(yōu)化的傳感器布置方法研究

張 恒， 李世其， 劉世平， 張 哲， 王 躍

(華中科技大學(xué) 機(jī)械科學(xué)與工程學(xué)院，武漢 430074)

一種聚類優(yōu)化的傳感器布置方法研究

張 恒， 李世其， 劉世平， 張 哲， 王 躍

(華中科技大學(xué) 機(jī)械科學(xué)與工程學(xué)院，武漢 430074)

復(fù)雜結(jié)構(gòu)試驗(yàn)/理論振型的匹配是模態(tài)參數(shù)型修正過(guò)程的重要內(nèi)容。以測(cè)量并獲取用于模態(tài)參數(shù)識(shí)別的最佳信息為目標(biāo)，實(shí)現(xiàn)布置在結(jié)構(gòu)上有限數(shù)量的傳感器能有效避免信息冗余，提出了一種聚類優(yōu)化的傳感器布置方法。根據(jù)結(jié)構(gòu)模態(tài)中各自由度振型的動(dòng)力相似性，應(yīng)用k-means聚類算法對(duì)自由度進(jìn)行自動(dòng)集結(jié)并分類。采用有效獨(dú)立法分別從各聚類自由度中搜索出模態(tài)分辨率最高的傳感器位置作為實(shí)際的測(cè)量位置。最后通過(guò)一個(gè)懸臂梁、一個(gè)懸臂薄板的數(shù)值分析和一個(gè)旋轉(zhuǎn)濾光輪組件的模態(tài)測(cè)試試驗(yàn)對(duì)該優(yōu)化布置方法進(jìn)行驗(yàn)證。分析結(jié)果表明，這種方法能有效選出獨(dú)立敏感性測(cè)點(diǎn)，并且具有較高的搜索效率。

傳感器布置；k-means聚類；有效獨(dú)立法；模態(tài)試驗(yàn)；模型驗(yàn)證

航天器結(jié)構(gòu)模型試驗(yàn)驗(yàn)證是結(jié)構(gòu)計(jì)算模型修正技術(shù)必須解決的關(guān)鍵性問(wèn)題。其中，試驗(yàn)?zāi)B(tài)參數(shù)的辨識(shí)精度很大程度上決定了模型修正技術(shù)的成敗和效率，而高質(zhì)量的測(cè)試數(shù)據(jù)則是試驗(yàn)?zāi)B(tài)參數(shù)辨識(shí)精度的保障[1]。隨著大型機(jī)械結(jié)構(gòu)日益復(fù)雜，結(jié)構(gòu)理論與試驗(yàn)?zāi)Ｐ推ヅ涞碾y度迅速加大。目前采用的對(duì)策是在模型試驗(yàn)驗(yàn)證過(guò)程中，利用結(jié)構(gòu)的先驗(yàn)理論模型進(jìn)行測(cè)試傳感器的優(yōu)化配置，選擇模態(tài)分辨率最高的傳感器位置作為實(shí)際的測(cè)量位置，使理論與實(shí)驗(yàn)?zāi)Ｐ蜐M足高度的相關(guān)性，從而準(zhǔn)確獲取試驗(yàn)驗(yàn)證模型[2]。傳統(tǒng)的傳感器優(yōu)化配置方法是一種次優(yōu)化方法。Kammer根據(jù)Fisher信息矩陣行列式最大化的思想提出了一種有效獨(dú)立法[3]，通過(guò)迭代刪除獨(dú)立貢獻(xiàn)最小的自由度最終確定傳感器的數(shù)目，這種方法可擴(kuò)展應(yīng)用于三向加速度傳感器的布置過(guò)程[4]。能量法是根據(jù)結(jié)構(gòu)自由度的模態(tài)動(dòng)能或單元應(yīng)變能選擇傳感器的位置[5]。Papadimitriou提出一種基于信息熵指標(biāo)的傳感器優(yōu)化方法，該方法是把模態(tài)參數(shù)估計(jì)的不確定性用信息熵指標(biāo)來(lái)度量，通過(guò)度量值的最小原則選擇傳感器[6]。然而，這些傳感器優(yōu)化布置方法對(duì)自由度數(shù)目的選取依賴試驗(yàn)者的主觀經(jīng)驗(yàn)，當(dāng)采用傳感器的數(shù)目大于感興趣的模態(tài)階數(shù)時(shí)，優(yōu)化方法選擇的傳感器表現(xiàn)出明顯的聚類特性[7]，并且過(guò)多的傳感器布置將不可避免引入冗余信息[8]。從工程應(yīng)用方面考慮，單純采用這些優(yōu)化方法并不理想。聚類算法為傳感器的優(yōu)化選擇提供了一種新途徑，采用k-means聚類算法可對(duì)動(dòng)力相似性的自由度進(jìn)行自動(dòng)集結(jié)分類，從而避免了對(duì)自由度數(shù)目的主觀選擇[9]。

針對(duì)以上分析，本研究根據(jù)結(jié)構(gòu)中各自由度振型的動(dòng)力相似性，采用k-means聚類算法對(duì)自由度進(jìn)行自動(dòng)分類，采用有效獨(dú)立法實(shí)現(xiàn)傳感器的優(yōu)化布置。以一個(gè)懸臂梁和一個(gè)懸臂板的數(shù)值仿真和一個(gè)濾光輪組件的模態(tài)試驗(yàn)為例，對(duì)傳感器測(cè)點(diǎn)選擇與優(yōu)化布置方法進(jìn)行探討，為有效獲得結(jié)構(gòu)敏感振動(dòng)狀態(tài)信息提供參考。

1 基本理論

1.1 計(jì)算模型

定義一個(gè)n自由度結(jié)構(gòu)動(dòng)力系統(tǒng)，其運(yùn)動(dòng)方程可表示為

(-ω2[M]+iω[C]+[K]X(ω)=F(ω)

(1)

式中：[M]、[C]、[K]分別表示結(jié)構(gòu)的質(zhì)量、阻尼和剛度矩陣；F(ω)為外載荷向量。對(duì)于無(wú)阻尼自由振動(dòng)系統(tǒng)，由n個(gè)特征值0≤λ1≤λ2≤…≤λn及其對(duì)應(yīng)的特征向量{φ1，φ2,…，φn}構(gòu)成的特征方程為

[K]φ=λ[M]φ

(2)

由動(dòng)力分析模態(tài)疊加原理可知，結(jié)構(gòu)的響應(yīng)可以表示為

{x}=Φ{q}

(3)

式中：{x}為結(jié)構(gòu)的響應(yīng)向量；Φ為模態(tài)振型矩陣，{q}為模態(tài)坐標(biāo)向量。

1.2k-means聚類算法

自由度的動(dòng)力相似性主要表現(xiàn)為某些自由度在重要模態(tài)中的振型值相近，這些自由度在動(dòng)力載荷作用下的響應(yīng)也將近似相等。因此，可根據(jù)結(jié)構(gòu)中各自由度在重要模態(tài)中振型值的相似度進(jìn)行自動(dòng)類別劃分。k-means聚類算法是以衡量分類結(jié)果的標(biāo)準(zhǔn)測(cè)度函數(shù)作為聚類分析的收斂條件，標(biāo)準(zhǔn)測(cè)度函數(shù)通常采用歐氏距離平方和的形式表述

(4)

式中：k為類別總數(shù)；φ為屬于第i類振型Φi的振型值；mi為類別Φi的中心。

對(duì)k-means算法的步驟具體描述如下：①在振型集合Φ中任選k個(gè)樣本作為k個(gè)初始聚類中心；②對(duì)于其余非聚類中心的振型值，根據(jù)他們與這些聚類中心的相似度(歐氏距離)，分別將他們劃分至與其最相近的聚類中心所在的類別；③更新每個(gè)類別的聚類中心(該聚類中所有振型值的均值)；④重復(fù)步驟②～③，直至標(biāo)準(zhǔn)測(cè)度函數(shù)E收斂。

1.3 有效獨(dú)立法

有效獨(dú)立法(EFI)的基本思想是從所有可能的測(cè)點(diǎn)出發(fā)，使選擇的測(cè)點(diǎn)能保留目標(biāo)模態(tài)具有最大的線性無(wú)關(guān)性。該矩陣可表述為

Q=φTφ

(5)

根據(jù)矩陣行列式最大準(zhǔn)則來(lái)評(píng)價(jià)構(gòu)造的Fisher信息矩陣，采用逐步消除法進(jìn)行迭代搜索，測(cè)點(diǎn)的選擇依賴有效獨(dú)立矩陣D，D可表述為

D=φQ-1φT

(6)

D為冪等矩陣，它的跡等于秩，其對(duì)角線上的元素Di表示第i個(gè)測(cè)點(diǎn)對(duì)矩陣D的貢獻(xiàn)。每次刪除獨(dú)立貢獻(xiàn)最小的值，即

det(Q)=det(Q0)(1-Di)

(7)

式中：Q0為初始Fisher信息矩陣，則在模態(tài)振型矩陣φ中刪除對(duì)應(yīng)的列向量，這樣就能從全部的待選測(cè)點(diǎn)中逐步刪除有效獨(dú)立貢獻(xiàn)最小的測(cè)點(diǎn)，保留對(duì)振型有效獨(dú)立貢獻(xiàn)較大的測(cè)點(diǎn)。

2 傳感器聚類優(yōu)化布置方法設(shè)計(jì)

傳感器優(yōu)化布置的目的是使獲得的模態(tài)空間估計(jì)最佳，常采用模態(tài)振型構(gòu)建反映結(jié)構(gòu)動(dòng)態(tài)特性的Fisher信息矩陣。然而，當(dāng)兩個(gè)傳感器在同一方向上獲得的振型值相近時(shí)，選擇一個(gè)傳感器即可表征該方向上的振動(dòng)狀態(tài)信息。本研究根據(jù)重要模態(tài)中振型值的相似性，采用k-means聚類算法對(duì)自由度進(jìn)行自動(dòng)集結(jié)分類，在各聚類自由度中采用有效獨(dú)立逐步刪除對(duì)目標(biāo)模態(tài)線性支持度較小的測(cè)點(diǎn)，最終得到傳感器的最優(yōu)布置方案。該方法的流程如圖1所示，具體的算法描述如下：

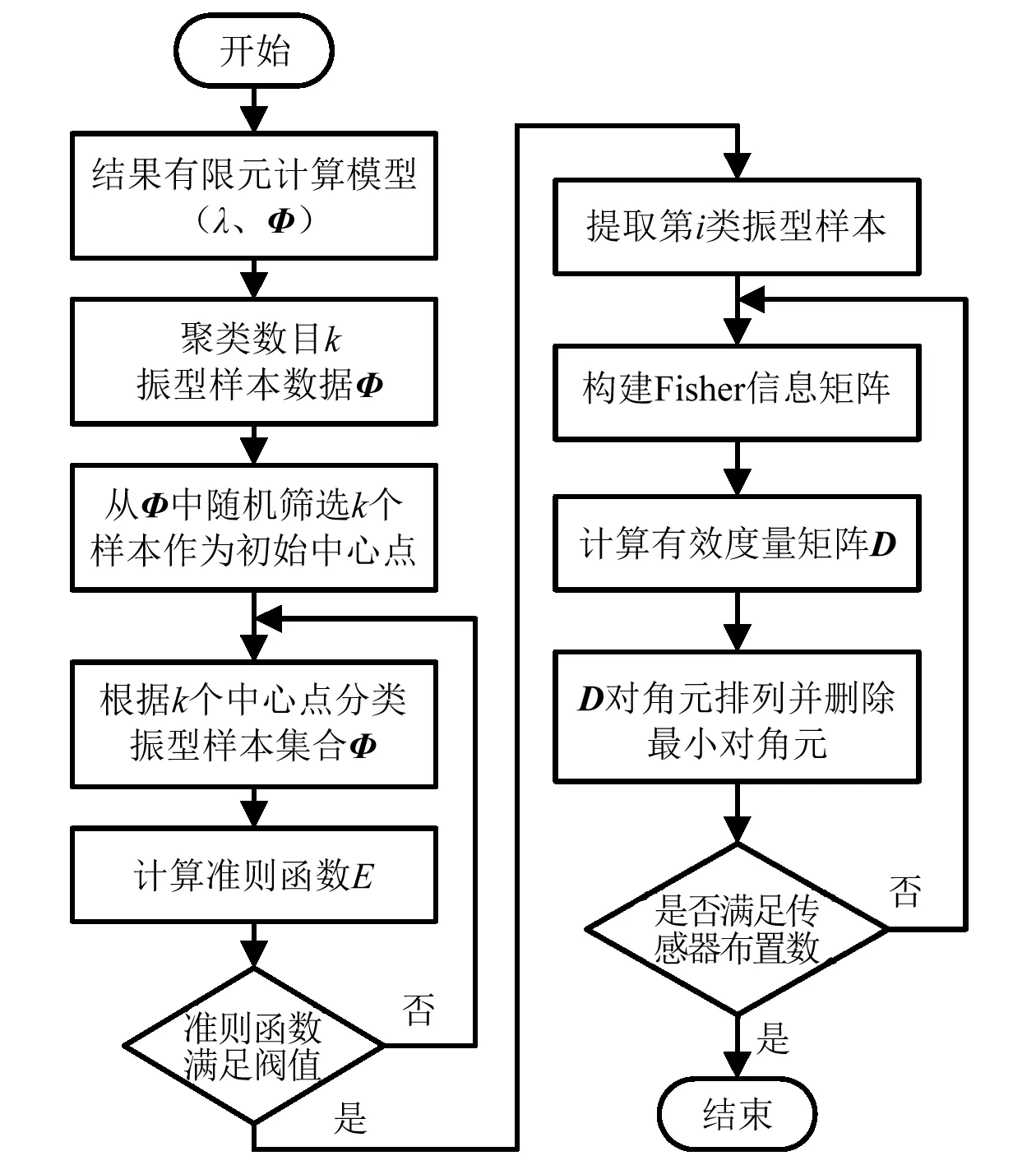
圖1 傳感器優(yōu)化布置流程圖Fig.1 Flow chart of optimal sensor placement

步驟1 建立結(jié)構(gòu)有限元分析計(jì)算模型，確定自由度數(shù)Ns，計(jì)算結(jié)構(gòu)各階模態(tài)振型φ，并選擇出重要模態(tài)數(shù)Nm；

步驟2 以重要模態(tài)振中的振型值作為樣本屬性，采用k-means聚類算法將各自由度進(jìn)行自動(dòng)分類，以標(biāo)準(zhǔn)測(cè)度函數(shù)E為判據(jù)，直至準(zhǔn)則函數(shù)滿足收斂條件；

步驟3 對(duì)每一個(gè)聚類樣本采用有效獨(dú)立法，計(jì)算待選傳感器的有效度量D，根據(jù)Di大小刪除對(duì)應(yīng)有效獨(dú)立貢獻(xiàn)值最小的測(cè)點(diǎn)，重復(fù)步驟3直到達(dá)到要求的測(cè)點(diǎn)數(shù)，從而以盡可能少的傳感器測(cè)量獲得更多的結(jié)構(gòu)振動(dòng)信息。

3 數(shù)值算例

3.1 算例1：簡(jiǎn)單梁

分析了文獻(xiàn)[7]中的算例，采用一個(gè)懸臂梁用于描述本研究提出方法的數(shù)值性能。懸臂梁總長(zhǎng)0.530 7 m，矩形截面尺寸為0.003 2 m×0.001 9 m，材料密度為2 700 kg/m3，彈性模量為7.1×1 010 N/m2。有限元模型包含30個(gè)單元，總自由度數(shù)為60，根據(jù)歐拉-伯努利梁理論建立梁?jiǎn)卧⒂?jì)算獲得各階模態(tài)振型。模型的示意圖如下所示。前3階模態(tài)主要為Y方向的振動(dòng)，以Y方向的30個(gè)自由度前3階振型值為屬性，采用k-means方法進(jìn)行自由度聚類劃分，聚類數(shù)為3。其中，隸屬于相同類別的自由度用相同的符號(hào)表示，如圖2(c)。

圖2 懸臂梁的傳感器優(yōu)化布置Fig.2 Optimal sensor placement of cantilever beam

采用EFI方法分別對(duì)文獻(xiàn)[7]中的方法和本研究提出的方法進(jìn)行比較，其中，迭代刪除后保留5個(gè)傳感器位置。傳感器的全局搜索結(jié)果與聚類逐步搜索結(jié)果見(jiàn)表1，測(cè)點(diǎn)布置情況如圖2(a)和(b)。可以看出，本研究提出方法選擇的傳感器位置分布更加均衡，從而有效避免了傳感器之間的聚類情況，使測(cè)得的結(jié)構(gòu)信息更加完備。

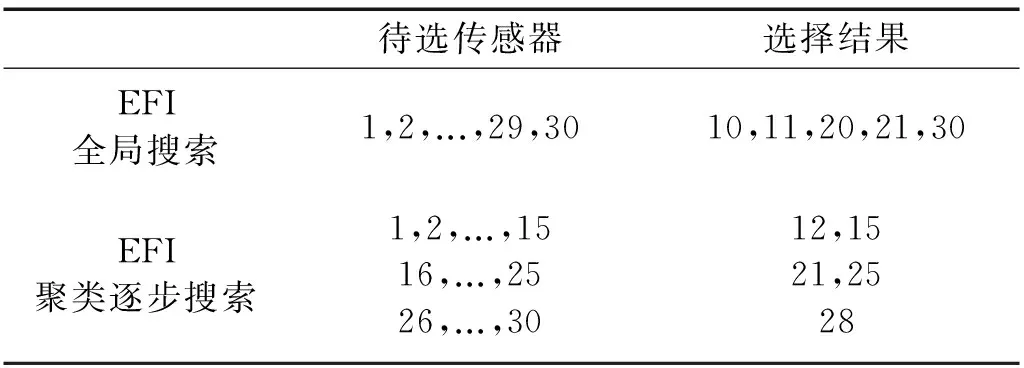
表1 兩種EFI搜索方法的對(duì)比結(jié)果

3.2 算例2：懸臂板

第二個(gè)數(shù)值算例采用空間相機(jī)的次鏡輻板，單個(gè)輻板可簡(jiǎn)化為簡(jiǎn)單懸臂板結(jié)構(gòu)。如圖3所示，懸臂板包含80個(gè)單元，100個(gè)節(jié)點(diǎn)(長(zhǎng)度方向20個(gè)節(jié)點(diǎn)，寬度方向5個(gè)節(jié)點(diǎn))。根據(jù)薄板彎曲理論，建立薄板的彎曲單元。板單元的幾何參數(shù)分別為：長(zhǎng)度a=0.02 m，寬度b=0.02 m，厚度h=0.005 m；材料參數(shù)為：彈性模量E=1.47×1 011 N/m2，材料密度ρ=8 180 kg/m3，泊松比v=0.3，通過(guò)有限元法求解懸臂板的模態(tài)。采用本研究提出的傳感器優(yōu)化布置過(guò)程，當(dāng)聚類數(shù)分別取3和4時(shí)，測(cè)點(diǎn)的布置結(jié)果如圖3所示。從圖中可以看出，絕大多數(shù)測(cè)點(diǎn)布置在懸臂板的邊緣，當(dāng)懸臂板劃分更多的聚類數(shù)時(shí)，測(cè)點(diǎn)的布置更加均衡，但計(jì)算量更大。

圖3 懸臂板的傳感器優(yōu)化布置Fig.3 Optimal sensor placement of cantilever plate

4 試驗(yàn)分析

以空間相機(jī)旋轉(zhuǎn)濾光輪組件為研究對(duì)象，開(kāi)展該組件的模態(tài)分析與試驗(yàn)，重點(diǎn)分析了該組件的傳感器優(yōu)化布置。首先，構(gòu)建該組件的有限元模型，建立的有限元模型共有11 144個(gè)單元，16 707個(gè)節(jié)點(diǎn)，如圖4所示。由于結(jié)構(gòu)內(nèi)部節(jié)點(diǎn)無(wú)法被測(cè)量，因此待選測(cè)點(diǎn)僅限于濾光輪支撐結(jié)構(gòu)的上表面，共計(jì)935個(gè)節(jié)點(diǎn)。

對(duì)該組件進(jìn)行模態(tài)分析，前六階模態(tài)為剛體模態(tài)，第七階為軸承旋轉(zhuǎn)模態(tài)，濾光輪的一階彈性模態(tài)從第八階模態(tài)開(kāi)始，該結(jié)構(gòu)的前5階彈性模態(tài)頻率見(jiàn)表2。對(duì)該結(jié)構(gòu)的模態(tài)振型描述如下：第一階是沿垂直面的彎曲模態(tài)；第二階是沿對(duì)角面的彎曲模態(tài)；第三階是沿Z方向的上下振動(dòng)；第四階是沿對(duì)角線方向的組合模態(tài)；第五階是各方向上各階彎曲模態(tài)的組合。

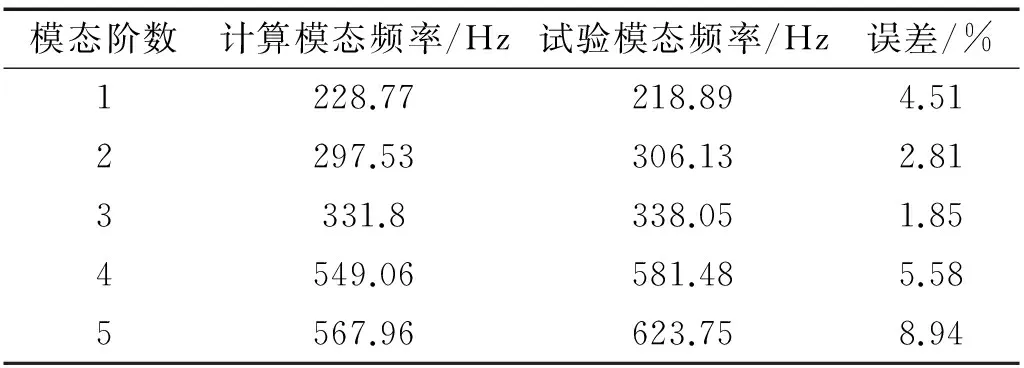
表2 濾光輪組件的前五階模態(tài)頻率

采用本研究提出的聚類優(yōu)化傳感器布置方法從待選測(cè)點(diǎn)中選出反映結(jié)構(gòu)主響應(yīng)特征的測(cè)點(diǎn)，傳感器的數(shù)目為主要模態(tài)的3倍(前五階模態(tài)為主要模態(tài))，最終獲得的15個(gè)傳感器位置如圖4中箭頭所示。

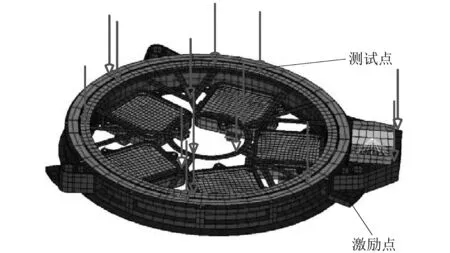
圖4 旋轉(zhuǎn)濾光輪組件的測(cè)點(diǎn)選擇Fig.4 Sensor selection of the filter wheel assembly

為進(jìn)一步驗(yàn)證模型的有效性，對(duì)濾光輪組件進(jìn)行模態(tài)試驗(yàn)。綜合上述過(guò)程獲得的傳感器位置，為更全

面測(cè)得結(jié)構(gòu)的狀態(tài)信息，在濾光輪上補(bǔ)充部分傳感器，共采用36個(gè)加速度傳感器，其實(shí)際測(cè)試如圖5所示，采用力錘敲擊圖中所示的激勵(lì)點(diǎn)。信號(hào)采集設(shè)備包括LMS信號(hào)采集儀和PCB三向加速度傳感器，采樣頻率為4 096 Hz。多次測(cè)量后獲得該結(jié)構(gòu)的模態(tài)特征，通過(guò)辨識(shí)方法獲得的試驗(yàn)?zāi)B(tài)頻率見(jiàn)表2，模態(tài)測(cè)試試驗(yàn)振型的原始數(shù)據(jù)見(jiàn)表3。表3中分別列舉了36個(gè)測(cè)點(diǎn)前五階模態(tài)試驗(yàn)的振型數(shù)據(jù)。各階振型如圖6所示，從圖中可以看出，濾光輪結(jié)構(gòu)的實(shí)測(cè)振型與計(jì)算模態(tài)振型基本相同，說(shuō)明本研究提出的傳感器布置方法有效。

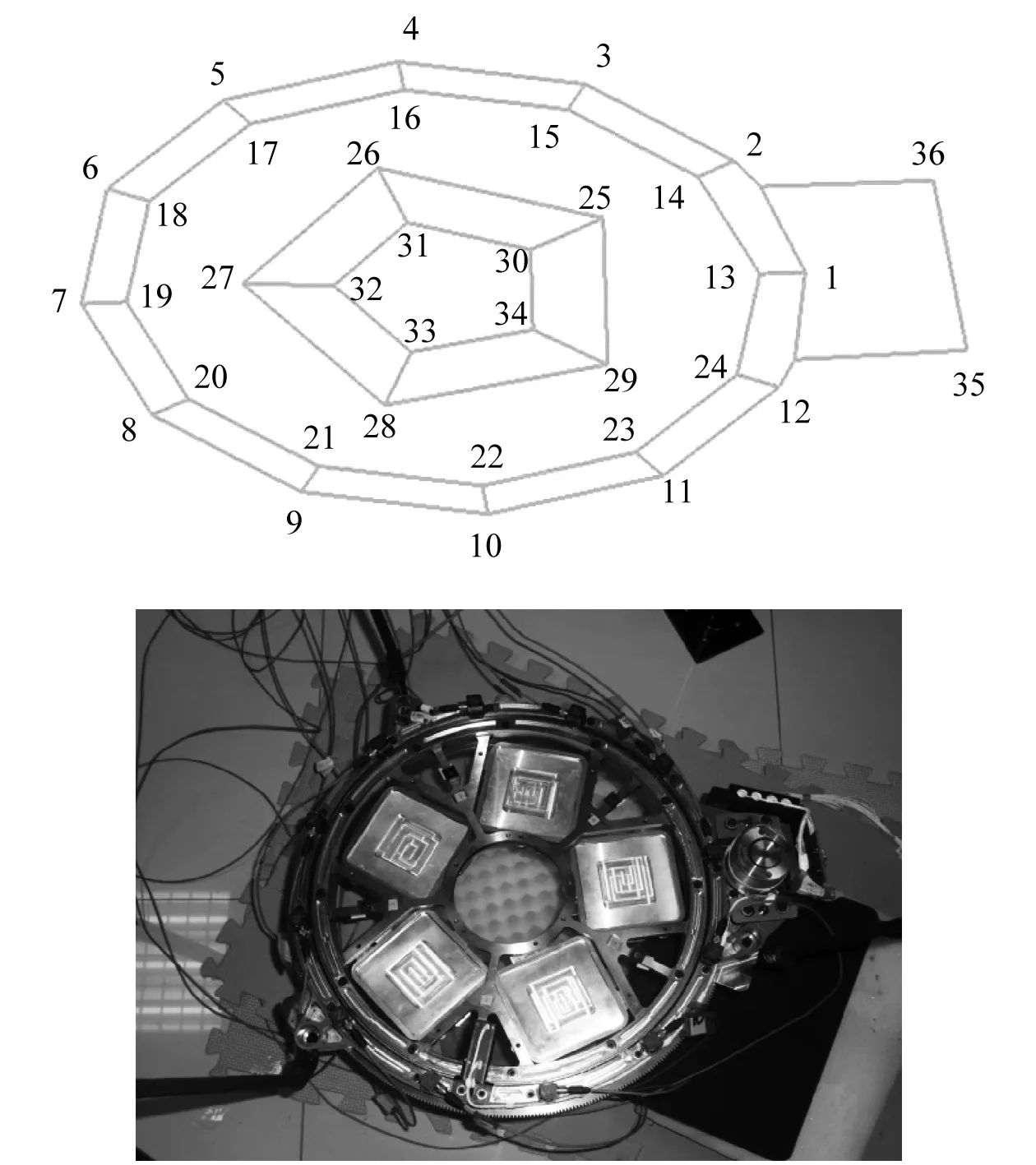
圖5 濾光輪組件的實(shí)際測(cè)點(diǎn)布置Fig.5 Actual sensor placement of the filter wheel assembly

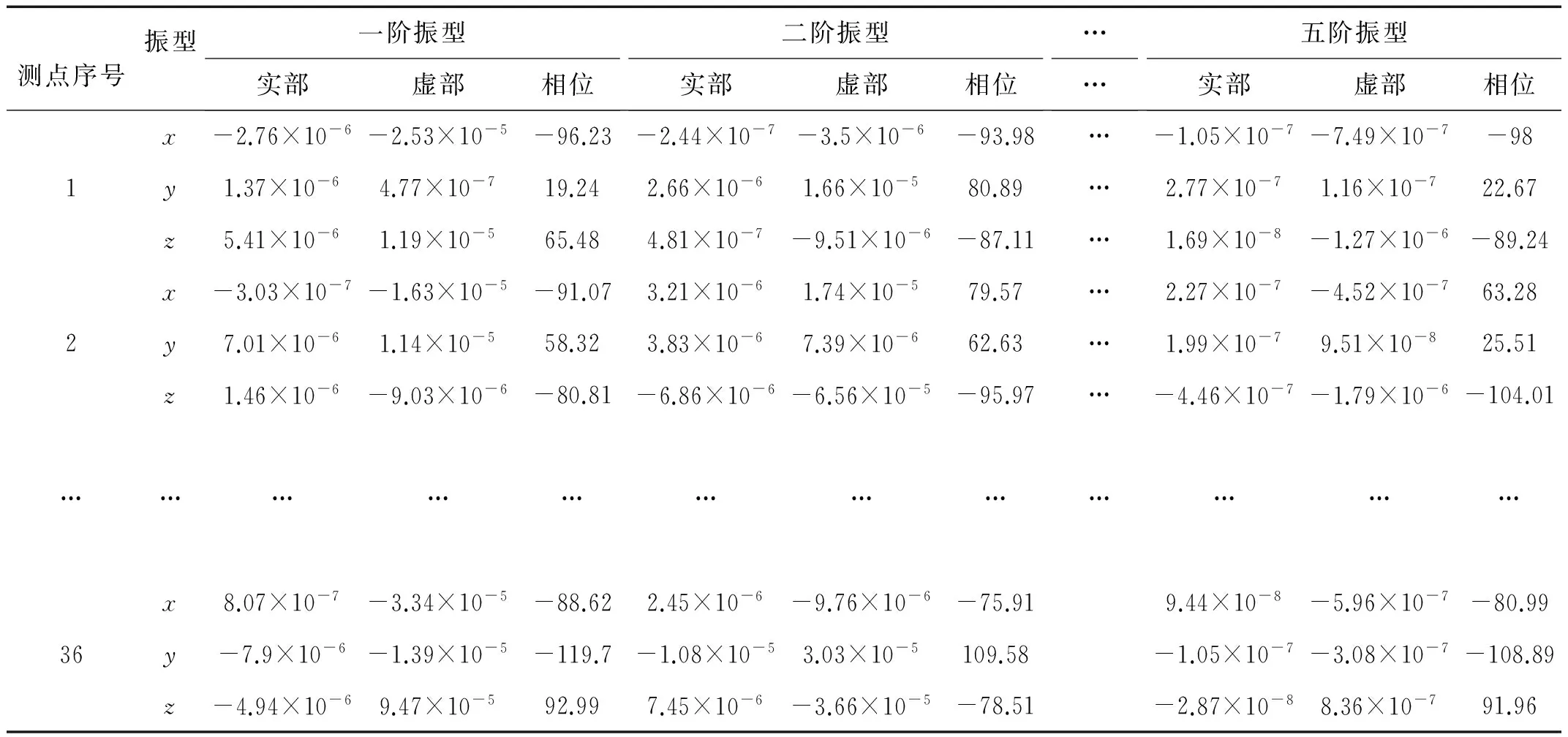
測(cè)點(diǎn)序號(hào)振型一階振型實(shí)部虛部相位二階振型實(shí)部虛部相位……五階振型實(shí)部虛部相位x-2.76×10-6-2.53×10-5-96.23-2.44×10-7-3.5×10-6-93.98…-1.05×10-7-7.49×10-7-981y1.37×10-64.77×10-719.242.66×10-61.66×10-580.89…2.77×10-71.16×10-722.67z5.41×10-61.19×10-565.484.81×10-7-9.51×10-6-87.11…1.69×10-8-1.27×10-6-89.24x-3.03×10-7-1.63×10-5-91.073.21×10-61.74×10-579.57…2.27×10-7-4.52×10-763.282y7.01×10-61.14×10-558.323.83×10-67.39×10-662.63…1.99×10-79.51×10-825.51z1.46×10-6-9.03×10-6-80.81-6.86×10-6-6.56×10-5-95.97…-4.46×10-7-1.79×10-6-104.01………………………………x8.07×10-7-3.34×10-5-88.622.45×10-6-9.76×10-6-75.919.44×10-8-5.96×10-7-80.9936y-7.9×10-6-1.39×10-5-119.7-1.08×10-53.03×10-5109.58-1.05×10-7-3.08×10-7-108.89z-4.94×10-69.47×10-592.997.45×10-6-3.66×10-5-78.51-2.87×10-88.36×10-791.96

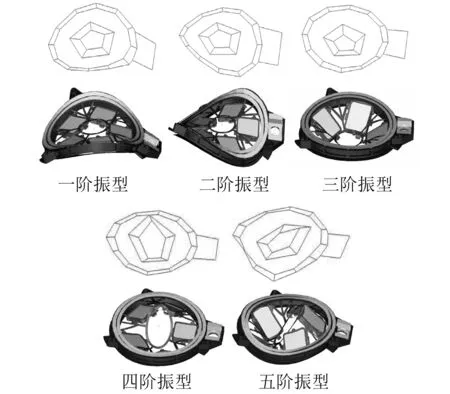
圖6 濾光輪組件的前五階模態(tài)振型Fig.6 The first five modal shape of the filter wheel assembly

5 結(jié) 論

為實(shí)現(xiàn)有限數(shù)量的傳感器最大程度反映結(jié)構(gòu)系統(tǒng)信息，本研究提出了一種聚類優(yōu)化的傳感器布置方法。該方法以結(jié)構(gòu)主模態(tài)振型值為屬性，采用k-means聚類算法對(duì)各自由度進(jìn)行自動(dòng)分類，采用有效獨(dú)立法從各聚類自由度中篩選出模態(tài)分辨率最高的測(cè)點(diǎn)作為實(shí)際的測(cè)量位置。一個(gè)懸臂梁和一個(gè)懸臂板的數(shù)值算例分析結(jié)果表明，采用本研究提出的傳感器優(yōu)化布置方法能使結(jié)構(gòu)上布置的測(cè)點(diǎn)分布更加均衡；當(dāng)選取更多的分類數(shù)時(shí)，獲得的布置測(cè)點(diǎn)更加精細(xì)，卻增加的計(jì)算量。某型號(hào)航天器旋轉(zhuǎn)濾光輪組件的動(dòng)力學(xué)試驗(yàn)驗(yàn)證分析結(jié)果表明，本文提出的傳感器優(yōu)化布置方法能有效獲取獨(dú)立敏感性測(cè)點(diǎn)，并且具有較高的迭代搜索效率，該方法能為復(fù)雜結(jié)構(gòu)航天器的傳感器優(yōu)化布置提供了一種新途徑。

[1] 丁繼鋒，韓增堯，馬興瑞. 大型復(fù)雜航天器結(jié)構(gòu)有限元模型的驗(yàn)證策略研究[J]. 宇航學(xué)報(bào), 2010, 31(2): 547-555. DING Jifeng, HAN Zengyao, MA Xingrui. Finite element model verification strategy of large complex spacecraft [J]. Journal of Astronautics, 2010, 31(2): 547-555.

[2] 秦仙蓉. 基于靈敏度分析的結(jié)構(gòu)計(jì)算模型修正技術(shù)及相關(guān)問(wèn)題研究[D]. 南京:南京航空航天大學(xué)，2001.

[3] KAMMER D C. Sensor placement for on-orbit modal identification and correlation of large space structures [J]. Journal of Guidance, Control and Dynamics, 1991, 14(2): 251-259.

[4] KAMMER D C, TINKER M L. Optimal placement of triaxial accelerometers for modal vibration tests [J]. Mechanical Systems and Signal Processing, 2004, 18(2): 29-41.

[5] HEMEZ F M, FARHAT C. An energy based optimum sensor placement criterion and its application to structural damage detection [C]∥ Proceedings of the 12th International Conference on Modal Analysis, Society of Experimental Mechanics. Honolulu, Hawaii, 1994.

[6] PAPADIMITRIOU C, BECK J L. Entropy-based optimal sensor location for structural model updating [J]. Journal of Vibration and Control, 2000, 6(5): 781-800.

[7] FRISWELL M I, TRIGUERO R C. Clustering of sensor locations using the effective independence method [J]. AIAA Journal, 2015, 53(5): 1388-1390.

[8] SEONGMIN C, SUNGMIN B, KIM K O, et al. Structural system identification using degree of freedom-based reduction and hierarchical clustering algorithm [J]. Journal of Sound and Vibration, 2015, 346 (25): 139-152.

[9] 李成濤,肖儀清,歐進(jìn)萍. 基于聚類算法和自由度集結(jié)的柔性結(jié)構(gòu)模型降階研究[J]. 計(jì)算力學(xué)學(xué)報(bào), 2012, 29(2): 236-241. LI Chengtao, XIAO Yiqing, OU Jinping. Study on the model reduction for flexible structure based on clustering algorithm and DOFs concentration [J]. Chinese Journal of Computational Mechanics, 2012, 29(2): 236-241.

Optimal sensor placement by using clustering method

ZHANG Heng, LI Shiqi, LIU Shiping, ZHANG Zhe, WANG Yue

(School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

The match of experimental/theoretical models of complex structures is an important part in modal parameter modification. To measure and obtain the best information, a clustering optimal method for sensor placement was proposed. The method can effectively avoid the information redundancy when using a limited number of sensors. According to the dynamic similarity of the mode shape values in important modes, the DOFs were auto-clustered by usingk-means clustering algorithm. The effective independent method was used to search out the sensor locations with the highest modal resolution from each cluster. Finally, the numerical analyses on a cantilever beam and a cantilever plate and the modal test of a filter wheel assembly were carried out to verify the optimization method. The results show that the method can effectively select the independent sensitive locations with a much higher search efficiency.

sensor placement;k-means clustering; effective independent method; modal test; model validation

國(guó)家重大科技專項(xiàng)

2016-02-29 修改稿收到日期： 2016-05-30

張恒 男，博士生，1988年生

劉世平 男，博士，副教授，1971年生

TH113.1

A

10.13465/j.cnki.jvs.2017.14.009