高光譜影像的近鄰加權(quán)拉普拉斯降維方法
路 易, 郭 靜, 于少波
(1. 裝備學(xué)院 研究生管理大隊(duì), 北京 101416; 2. 裝備學(xué)院 復(fù)雜電子系統(tǒng)仿真實(shí)驗(yàn)室, 北京 101416)
高光譜影像的近鄰加權(quán)拉普拉斯降維方法
路 易1, 郭 靜2, 于少波1
(1. 裝備學(xué)院 研究生管理大隊(duì), 北京 101416; 2. 裝備學(xué)院 復(fù)雜電子系統(tǒng)仿真實(shí)驗(yàn)室, 北京 101416)
針對(duì)高光譜影像數(shù)據(jù)中存在信息冗余和非線性結(jié)構(gòu)的現(xiàn)象,以及數(shù)據(jù)分布不均勻時(shí)拉普拉斯特征映射近鄰點(diǎn)選擇不恰當(dāng)?shù)膯?wèn)題,提出了一種基于Cam加權(quán)距離的拉普拉斯改進(jìn)算法,用于高光譜影像數(shù)據(jù)降維以壓縮數(shù)據(jù)量并提高分類(lèi)精度。首先對(duì)波段分組去除奇異波段,然后用基于Cam加權(quán)距離的拉普拉斯特征映射算法對(duì)剩余數(shù)據(jù)降維,最后將結(jié)果輸入最小距離分類(lèi)器進(jìn)行高光譜影像分類(lèi)。通過(guò)Indiana Pines數(shù)據(jù)集進(jìn)行驗(yàn)證,實(shí)驗(yàn)結(jié)果表明:與線性降維主成分分析法和非線性降維拉普拉斯特征映射相比,基于Cam加權(quán)距離的拉普拉斯特征映射算法分類(lèi)精度更高。
Cam加權(quán)距離;拉普拉斯特征映射;非線性降維;波段選擇
高光譜圖像數(shù)據(jù)包括地物的二維空間信息和光譜波段信息,具有“圖像立方體”的形式和結(jié)構(gòu)。高光譜圖像數(shù)據(jù)量大、數(shù)據(jù)冗余嚴(yán)重、譜間相關(guān)性強(qiáng),為得到精確的分類(lèi)結(jié)果,分類(lèi)前對(duì)高光譜圖像數(shù)據(jù)進(jìn)行降維處理尤為重要。高光譜數(shù)據(jù)降維方法主要分為2類(lèi):特征選擇和特征提取。高光譜圖像的特征選擇是波段組合優(yōu)化問(wèn)題,即選擇出信息量較大、相關(guān)性較小、類(lèi)別可分性較好的波段組合。與特征選擇相比,特征提取是對(duì)原始高光譜數(shù)據(jù)進(jìn)行數(shù)學(xué)變換,然后選取變換后的前n個(gè)特征作為降維之后的n個(gè)成分,實(shí)現(xiàn)數(shù)據(jù)降維[1]。
特征提取可以挖掘原始數(shù)據(jù)的隱含信息,可分為線性特征提取和非線性特征提取。主成分分析法(PrincipalComponentAnalysis,PCA)[2]和最大噪聲分離變換(MaximumNoiseFraction,MNF)是目前應(yīng)用廣泛的線性特征提取方法。但實(shí)際上,在高光譜圖像數(shù)據(jù)的同類(lèi)地物中和類(lèi)間都存在非線性特性,在光譜維上尤為明顯。如果用傳統(tǒng)的線性模型對(duì)高光譜圖像進(jìn)行處理無(wú)疑會(huì)丟失有用的信息。近年來(lái),非線性流形學(xué)習(xí)方法在高光譜降維取得一定成果。常用的流形學(xué)習(xí)算法主要包括等距映射[3]、局部線性嵌入[4]、拉普拉斯特征映射(LE)[5]、局部切空間排列算法[6]等。拉普拉斯特征映射方法與線性方法PCA和非線性的其他流形學(xué)習(xí)方法相比,在低維流形保持能力、抵抗噪聲能力、處理稀疏數(shù)據(jù)能力以及算法計(jì)算復(fù)雜度上都有一定的優(yōu)勢(shì)。但在參數(shù)選擇、鄰域計(jì)算、大尺度應(yīng)用等方面仍需進(jìn)一步研究。提出基于Cam加權(quán)距離的拉普拉斯特征映射,即在鄰域計(jì)算上做出了改進(jìn)。具體做法為:用Cam加權(quán)距離替代拉普拉斯特征映射構(gòu)建鄰域時(shí)所用的歐氏距離。
本文先通過(guò)相關(guān)系數(shù)矩陣對(duì)原始數(shù)據(jù)進(jìn)行波段選擇,再分別用主成分分析法、拉普拉斯特征映射和基于Cam加權(quán)距離的拉普拉斯進(jìn)行降維,將降維后的結(jié)果輸入最小距離分類(lèi)器進(jìn)行高光譜圖像分類(lèi),比較各方法的總體分類(lèi)精度和計(jì)算時(shí)間,實(shí)驗(yàn)結(jié)果表明:基于Cam加權(quán)距離的拉普拉斯可以得到更好的效果。
1 高光譜影像降維
首先對(duì)高光譜影像原始數(shù)據(jù)進(jìn)行波段選擇,在這一過(guò)程中用到了自動(dòng)子空間劃分的相關(guān)理論。自動(dòng)子空間劃分是高光譜影像常用到的特征選擇方法。本文用此方法先去除原始數(shù)據(jù)中少量的奇異波段,然后對(duì)剩下的數(shù)據(jù)進(jìn)行非線性降維。本文提出的基于Cam加權(quán)距離的拉普拉斯降維方法是在拉普拉斯特征映射算法上進(jìn)行了改進(jìn)。拉普拉斯特征映射是近年來(lái)應(yīng)用到高光譜影像的非線性特征提取方法[7]。
1.1 自動(dòng)子空間劃分
自動(dòng)子空間劃分(Auto-SubspacePartition,ASP)方法通過(guò)定義波段相關(guān)系數(shù)矩陣及其近鄰可傳遞相關(guān)矢量,將高光譜數(shù)據(jù)空間劃分為適合的數(shù)據(jù)子空間。這種劃分方法有著充分的理論依據(jù),反映了數(shù)據(jù)的局部特性[8]。在對(duì)高光譜影像進(jìn)行波段選擇時(shí),根據(jù)高光譜影像具有相鄰譜段相關(guān)性強(qiáng)的特點(diǎn),通常用此方法結(jié)合波段指數(shù)尋找最佳波段。本文提出了在特征提取前首先對(duì)原始數(shù)據(jù)所有波段進(jìn)行分組,依據(jù)式(1)去除相關(guān)性極小的奇異波段,然后再進(jìn)行特征提取的改進(jìn)方案。
(1)
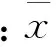
1.2 拉普拉斯特征提取方法

1) 計(jì)算像素點(diǎn)xi和xj的歐氏距離,構(gòu)建鄰域圖G。當(dāng)xj是xi鄰域k中的點(diǎn)時(shí),xi與xj之間存在邊長(zhǎng)為兩者歐氏距離的無(wú)向邊。
2) 計(jì)算G每條邊的權(quán)重,得到權(quán)重矩陣W。兩像素點(diǎn)間的權(quán)重系數(shù)
(2)
式中,σ2為徑向基核函數(shù)的方差。如果xj不是xi鄰域k中的點(diǎn),則wij=0。
3) 通過(guò)極小化目標(biāo)函數(shù)計(jì)算低維嵌入坐標(biāo)Y。目標(biāo)函數(shù)為
E(Y)=∑ij(yi-yj)2wij
(3)
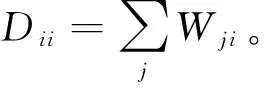
4∑ijyiyjwij=2yTLy
(4)
為求得唯一流形坐標(biāo),附加條件yTDy=1,于是
Ly=λDy
(5)
降維后的數(shù)據(jù)為除0外的d個(gè)特征值對(duì)應(yīng)的特征向量。
2 基于Cam加權(quán)距離的拉普拉斯降維
當(dāng)起始的樣本數(shù)量較少或樣本數(shù)據(jù)不是標(biāo)準(zhǔn)正態(tài)分布時(shí),基于歐氏距離來(lái)選取鄰域的方法并不能很好地構(gòu)建鄰域信息。目前已有實(shí)驗(yàn)證明高光譜數(shù)據(jù)空間存在非高斯分布結(jié)構(gòu)[9],并且在高光譜影像空間中,每類(lèi)樣本數(shù)據(jù)量多少不一。因此,在高光譜影像處理中直接應(yīng)用基于歐氏距離的傳統(tǒng)k近鄰方法效果不佳。 傳統(tǒng)k近鄰方法選擇最近的k個(gè)樣本,可能出現(xiàn)信息的冗余以及重要信息的丟失,如圖1所示。實(shí)線區(qū)域內(nèi)為k近鄰方法選擇的點(diǎn),對(duì)于不均勻的分布k近鄰選擇的點(diǎn)都集中在一側(cè),導(dǎo)致信息冗余且另一側(cè)信息丟失,因此這些近鄰點(diǎn)不能很好地重構(gòu)中心點(diǎn)。為此,本文用基于Cam加權(quán)距離的拉普拉斯方法對(duì)高光譜數(shù)據(jù)進(jìn)行降維,該方法可更合理地構(gòu)造出樣本點(diǎn)的鄰接信息,使得高光譜數(shù)據(jù)的低維流形更準(zhǔn)確的表達(dá)原始高維信息。
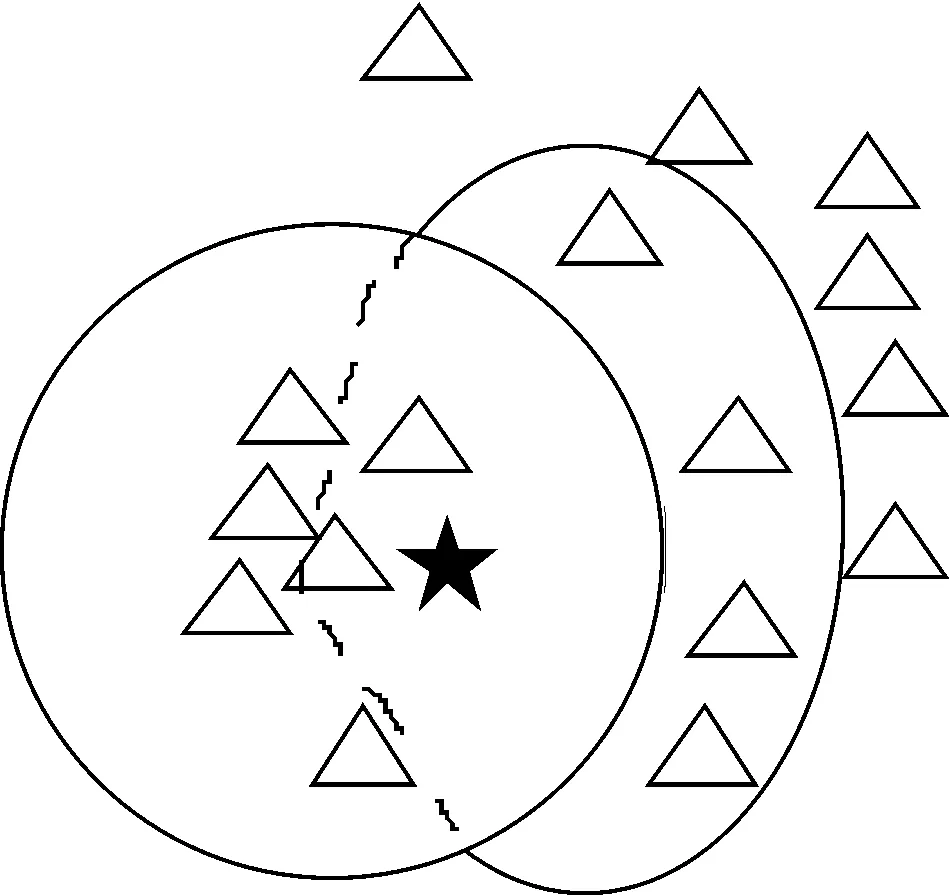
圖1 歐氏距離(實(shí)線)和加權(quán)距離(虛線)
2.1Cam分布
隨機(jī)向量X定義為
(6)
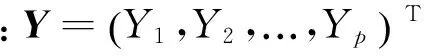
2.2 加權(quán)距離
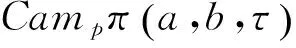

(7)
式中,a,b,τ為待估計(jì)參數(shù)。
2.3 參數(shù)估計(jì)
Y服從標(biāo)準(zhǔn)正態(tài)分布,其概率密度函數(shù)為
(8)
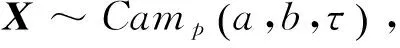
(9)
那么
E(X)=c1bτ
(10)
E(‖X‖)=c2a
(11)
式中,c1,c2為常量。
(12)

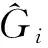
(13)
(14)
于是得到
(15)
將以上計(jì)算的Cam加權(quán)距離替代拉普拉斯特征提取中的歐式距離,可以解決數(shù)據(jù)分布不均的問(wèn)題,從而更好地對(duì)高光譜數(shù)據(jù)降維。
2.4 本文降維方法步驟
本文提出的高光譜影像數(shù)據(jù)降維方法將特征選擇和特征提取結(jié)合,流程如圖2所示。具體方法步驟為:
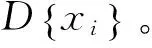
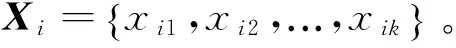
7) 由式(3)~式(5)計(jì)算低維嵌入坐標(biāo)Y。
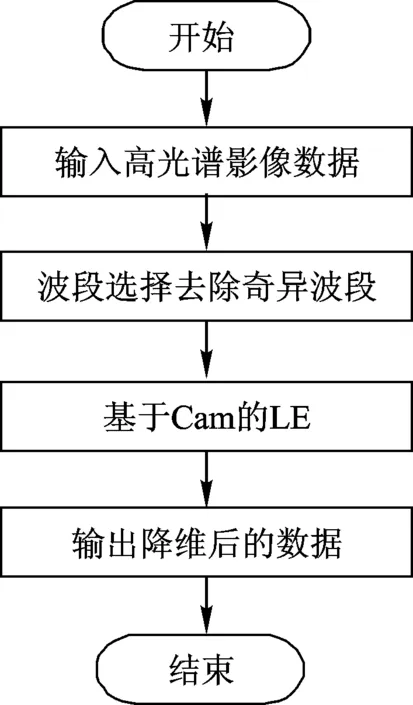
圖2 本文降維方法流程
3 實(shí) 驗(yàn)
3.1 實(shí)驗(yàn)數(shù)據(jù)
實(shí)驗(yàn)數(shù)據(jù)集為由成像光譜儀AVIRIS獲取的美國(guó)印第安納州某農(nóng)林混合實(shí)驗(yàn)場(chǎng)(IndianaPines)高光譜圖像。波長(zhǎng)范圍為0.4 ~ 2.5μm,空間分辨率為25m,空間大小為145×145個(gè)像素點(diǎn),從原始220個(gè)波段中去除水汽吸收波段和低信噪比波段([104~108],[150~163],220)后,保留了其中200個(gè)波段進(jìn)行數(shù)據(jù)處理。數(shù)據(jù)集中共有16類(lèi)地物。IndianaPines單一波段圖如圖3所示。

圖3 Indiana Pines單一波段圖
3.2 實(shí)驗(yàn)結(jié)果
對(duì)有200個(gè)波段的IndianaPines數(shù)據(jù)進(jìn)行波段選擇,計(jì)算相關(guān)系數(shù)矩陣。去除相關(guān)系數(shù)小于0.2的波段,剩余184個(gè)波段。首先對(duì)有184個(gè)波段的高光譜圖像用最小距離法進(jìn)行分類(lèi),總體分類(lèi)精度(OverallAccuracy,OA)為84.99%,比直接用200個(gè)波段進(jìn)行分類(lèi)提高1.1%。說(shuō)明此時(shí)有效去除了16個(gè)奇異波段。接著對(duì)含有184個(gè)波段的高光譜數(shù)據(jù)進(jìn)行實(shí)驗(yàn),分為用PCA、LE和基于Cam權(quán)重的LE進(jìn)行降維,將降維后的結(jié)果輸入最小距離分類(lèi)器比較實(shí)驗(yàn)結(jié)果。
圖4為PCA、LE和Cam-LE分別將184個(gè)波段的高光譜數(shù)據(jù)降到不同維數(shù)下的總體分類(lèi)精度條形圖。表1為對(duì)IndianaPines圖像分類(lèi)的運(yùn)行時(shí)間和總體分類(lèi)精度對(duì)照表。表1的第一行為對(duì)原始數(shù)據(jù)200個(gè)波段進(jìn)行分類(lèi)的總體分類(lèi)精度與運(yùn)行時(shí)間。其余的是對(duì)波段選擇后的184個(gè)波段繼續(xù)進(jìn)行降維并分類(lèi)的總體分類(lèi)精度和運(yùn)行時(shí)間。圖、表顯示的結(jié)果均為各方法參數(shù)調(diào)到分類(lèi)結(jié)果最優(yōu)情況下的實(shí)驗(yàn)結(jié)果。
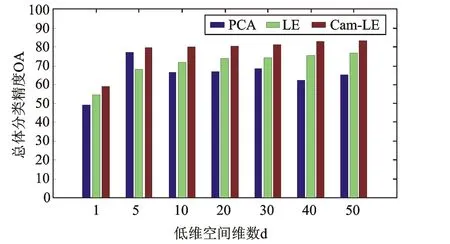
圖4 PCA、LE和Cam-LE不同維數(shù)下的總體分類(lèi)精度OA
實(shí)驗(yàn)結(jié)果顯示:用PCA降到5維時(shí),總體分類(lèi)精度最高;且全過(guò)程的運(yùn)行時(shí)間為9.11s,與流形學(xué)習(xí)方法相比時(shí)間最少。但在無(wú)先驗(yàn)知識(shí)的情況下不能直接選擇出最佳維數(shù)。本文用LE進(jìn)行降維時(shí),近鄰k選為9分類(lèi)精度最高。用不加改進(jìn)的拉普拉斯方法降維,只在降到5維時(shí)分類(lèi)精度低于PCA降維后的精度,在其他維數(shù)下分類(lèi)精度整體高于PCA降維后的分類(lèi)精度,且隨著維數(shù)增加精度呈上升趨勢(shì)。LE在計(jì)算時(shí)間上高于PCA,計(jì)算時(shí)間與近鄰數(shù)k有關(guān)。當(dāng)k一定時(shí),隨著維數(shù)增加計(jì)算時(shí)間也逐漸增加。用基于Cam加權(quán)距離的拉普拉斯降維選取k為12時(shí)分類(lèi)精度最高,分類(lèi)效果較好。但因?yàn)榛趫D構(gòu)建近鄰并且需要在k近鄰基礎(chǔ)上調(diào)整近鄰點(diǎn),所以計(jì)算時(shí)間最長(zhǎng)。
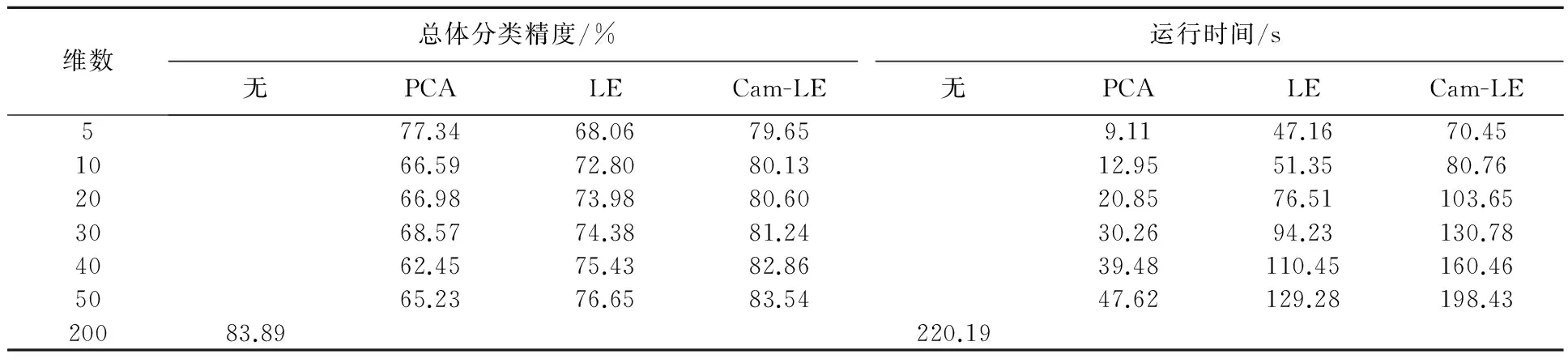
表1 不同維數(shù)下總體分類(lèi)精度和運(yùn)行時(shí)間
圖5為分別用PCA、LE和Cam-LE降維后維數(shù)不超過(guò)50時(shí),分類(lèi)精度最高的分類(lèi)圖像。圖5a)、圖5c)、圖5e)為理想分類(lèi)結(jié)果,圖5b)、圖5d)、圖5f)為實(shí)驗(yàn)分類(lèi)結(jié)果,每次實(shí)驗(yàn)均隨機(jī)分配顏色進(jìn)行分類(lèi)。圖5a)和圖5b)為用PCA降到5維時(shí)進(jìn)行分類(lèi)的分類(lèi)圖像,總體分類(lèi)精度為77.34%。圖5c)和圖5d)為用LE降到50維時(shí)進(jìn)行分類(lèi)的分類(lèi)圖像,選取k為9,此時(shí)總體分類(lèi)精度為76.65%。圖5e)和圖5f)為用Cam-LE降到50維時(shí)進(jìn)行分類(lèi)的分類(lèi)圖像,選取k為12,此時(shí)總體分類(lèi)精度為83.54%。由圖像可以明顯看出第三組,即用改進(jìn)后的拉普拉斯降維然后進(jìn)行分類(lèi)的效果最好。

a) 理想分類(lèi)結(jié)果 b) PCA分類(lèi)
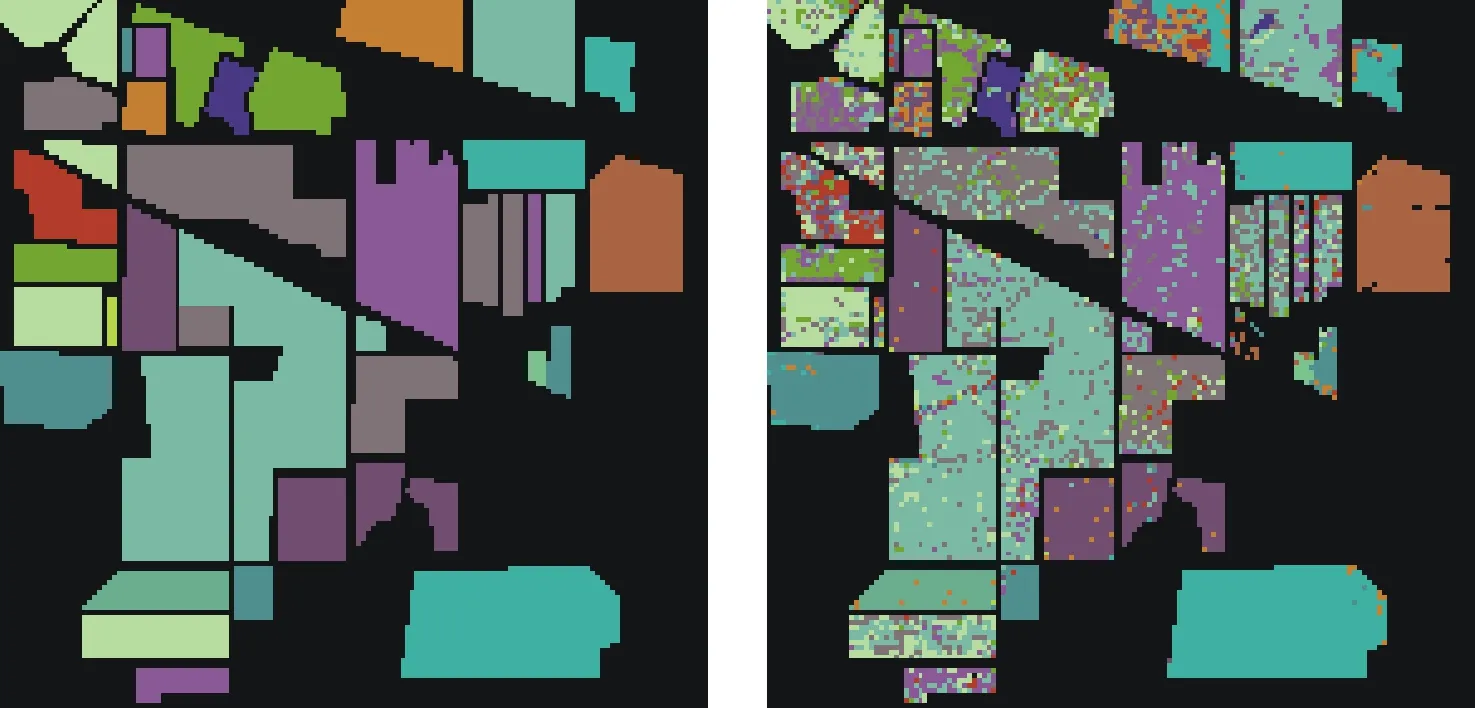
c) 理想分類(lèi)結(jié)果 d) LE分類(lèi)
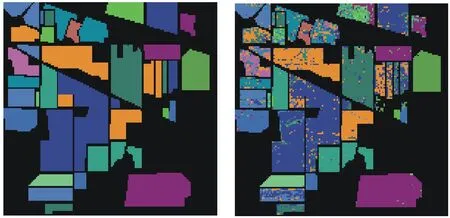
e) 理想分類(lèi)結(jié)果 f) Cam-LE分類(lèi) 圖5 PCA、LE、Cam-LE分類(lèi)圖
4 結(jié) 束 語(yǔ)
本文提出基于Cam加權(quán)距離的拉普拉斯高光譜圖像降維方法,結(jié)合最小距離分類(lèi)器用IndianaPines數(shù)據(jù)集進(jìn)行分類(lèi)實(shí)驗(yàn),并與傳統(tǒng)的線性降維PCA和非線性流形學(xué)習(xí)降維LE算法比較。結(jié)果證明:先進(jìn)行波段選擇可以去除奇異波段,提高分類(lèi)精度;基于Cam加權(quán)距離的拉普拉斯降維在分類(lèi)精度上優(yōu)于傳統(tǒng)線性PCA和非線性的流形學(xué)習(xí)降維LE;在計(jì)算時(shí)間上基于Cam加權(quán)距離的拉普拉斯與PCA和LE相比存在劣勢(shì),但與不降維直接進(jìn)行分類(lèi)相比,在分類(lèi)精度基本持平的情況下,計(jì)算時(shí)間更少。在本文方法基礎(chǔ)上,加入高光譜空間信息或利用各類(lèi)標(biāo)簽進(jìn)行半監(jiān)督拉普拉斯改進(jìn)是下一步研究的方向。
)
[1]張兵.高光譜圖像處理與信息提取前沿[J].遙感學(xué)報(bào),2016,20(5):1062-1090.
[2]JIA X,RICHARDS J A.Segmented principal components transformation for efficient hyperspectral remote sensing image display and classification[J].IEEE Trans.Geoscience and Remote Sensing,1999,37(1):538-542.
[3]杜培軍,王小美,譚琨,等.利用流形學(xué)習(xí)進(jìn)行高光譜遙感影像的降維與特征提取[J].武漢大學(xué)學(xué)報(bào)(信息科學(xué)版),2011,36(2):148-152.
[4]劉嘉敏,羅甫林,黃鴻,等.應(yīng)用相關(guān)近鄰局部線性嵌入算法的高光譜遙感影像分類(lèi)[J].光學(xué)精密工程,2014,22(6):1668-1676.
[5]孫偉偉,劉春,李巍岳.聯(lián)合改進(jìn)拉普拉斯特征映射和k-近鄰分類(lèi)器的高光譜影像分類(lèi)[J].武漢大學(xué)學(xué)報(bào)(信息科學(xué)版),2015,40(9):1151-1156.
[6]SUN W,HALEVY A,BENEDETTO J J,et al.Nonlinear dimensionality reduction via the ENH-LTSA method for hyperspectral image classification[J].Selected Topics in Applied Earth Observations & Remote Sensing IEEE Journal of,2014,7(2):375-388.
[7]錢(qián)進(jìn),鄧喀中,范洪冬.基于拉普拉斯特征映射高光譜遙感影像降維及其分類(lèi)[J].遙感信息,2012,27(5):3-7.
[8]蘇紅軍,杜培軍,盛業(yè)華.高光譜影像波段選擇算法研究[J].計(jì)算機(jī)應(yīng)用研究,2008,25(4):1093-1096.
[9]路威.面向目標(biāo)探測(cè)的高光譜影像特征提取與分類(lèi)技術(shù)研究[D].鄭州:中國(guó)人民解放軍信息工程大學(xué),2005:7.
[10]ZHOU C Y,CHEN Y Q.Improving nearest neighbor classification with cam weighted distance[J].Pattern Recognition,2006,39(4):635-645.
(編輯:李江濤)
Dimensionality Reduction for Hyperspectral Images Based on Cam Weighted Distance Laplacian Eigenmap
LU Yi1, GUO Jing2, YU Shaobo1
(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China; 2. Science and Technology on Complex Electronic System Simulation Laboratory, Equipment Academy, Beijing 101416, China)
In consideration of the information redundancy and intrinsic nonlinearities, and the irrelevancy of Laplacian Eigenmap k-nearest neighbor selected for the uneven distribution of hyperspectral image data, this paper presents an improved LE algorithm based on Cam weighted distance for hyperspectral image dimensionality reduction to compact feature representation and improve the accuracy of classification. First, the band is grouped for the removal of singular band, then the Cam weighted distance Laplacian Eigenmap is used to reduce the remaining data dimension, and finally, the results are put into the minimum distance classifier for hyperspectral image classification. By verification with the Indiana Pines data set, the experimental results show that compared with linear dimensionality reduction method of PCA and nonlinear method of LE, Cam weighted distance Laplacian Eigenmap algorithm gets higher classification accuracy.
Cam weighted distance; Laplacian eigenmap (LE); nonlinear dimensionality reduction; band selection
2017-04-17
部委級(jí)資助項(xiàng)目
路 易(1992—),女,碩士研究生,主要研究方向?yàn)楦吖庾V遙感。luyi9246@163.com
TP701
2095-3828(2017)03-0027-05
A DOI 10.3783/j.issn.2095-3828.2017.03.005

