機(jī)織物密度對字典學(xué)習(xí)紋理表征的影響

王 凱，吳 瑩，周 建，汪 軍,3，李立輕

(1. 東華大學(xué) 紡織學(xué)院，上海 201620；2. 江南大學(xué) 紡織服裝學(xué)院，江蘇 無錫 214122；3. 東華大學(xué) 紡織面料技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，上海 201620)

?

機(jī)織物密度對字典學(xué)習(xí)紋理表征的影響

王 凱1，吳 瑩1，周 建2，汪 軍1,3，李立輕1

(1. 東華大學(xué) 紡織學(xué)院，上海 201620；2. 江南大學(xué) 紡織服裝學(xué)院，江蘇 無錫 214122；3. 東華大學(xué) 紡織面料技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，上海 201620)

為探討紡織品表觀質(zhì)量的客觀、智能評定方法，使用不同密度的機(jī)織物圖像，采用子窗口樣本獲取方式作為學(xué)習(xí)樣本，以離散余弦字典作為初始學(xué)習(xí)字典，選擇基于最小二乘的字典學(xué)習(xí)算法求解用于表征織物紋理圖像的字典，再通過字典元素的線性組合對織物圖像進(jìn)行重構(gòu)。以均方誤差為指標(biāo)，首先討論織物圖像灰度值分布對字典學(xué)習(xí)算法重構(gòu)誤差的影響，然后對圖像灰度值進(jìn)行標(biāo)準(zhǔn)化處理，在此基礎(chǔ)上探討織物經(jīng)緯密度對重構(gòu)圖像誤差的影響。實(shí)驗(yàn)結(jié)果發(fā)現(xiàn)，當(dāng)字典個(gè)數(shù)等于9時(shí)，織物密度在150～360 根/10 cm之間，隨著織物密度的增加，平紋重構(gòu)圖像的均方誤差先變大，以后不再增加，而斜紋重構(gòu)圖像的均方誤差增大。

字典學(xué)習(xí)；機(jī)織物；紋理表征；密度

紡織品表觀質(zhì)量的客觀評定是控制生產(chǎn)質(zhì)量的重要環(huán)節(jié)之一。機(jī)織物在生產(chǎn)過程中，由于織物所采用的組織結(jié)構(gòu)、紗線的原料及線密度、織物的經(jīng)緯密度等各不相同，因此制成的織物在外觀上也不一樣。一般機(jī)織物是由互相垂直排列的經(jīng)紗和緯紗在織機(jī)上按一定規(guī)律交織而成，因此其表面的紋理具有一定的周期性。

隨著人工智能和模式識(shí)別技術(shù)的發(fā)展，采用計(jì)算機(jī)對機(jī)織物的紋理進(jìn)行表征研究，成為研究熱點(diǎn)之一。薛樂[1]利用Gabor變換和圖像融合的方法表征織物紋理，用于織物瑕疵的檢測；姚芳[2]采用自適應(yīng)小波三層分解的方法來表征機(jī)織物紋理，驗(yàn)證了該紋理表征方法的可行性；張軍[3]基于局部結(jié)構(gòu)統(tǒng)計(jì)的方法表征紋理，針對局部結(jié)構(gòu)統(tǒng)計(jì)中關(guān)于如何生成局部描述子和矢量量化2個(gè)問題進(jìn)行探究；張偉偉[4]提出了針對彩色和光照不均勻紋理圖像的特征提取及其分類方法；其他相關(guān)研究都取得了一定的進(jìn)展。

近年來，使用字典學(xué)習(xí)用于信號的壓縮和圖像去噪受到廣泛的關(guān)注，機(jī)織物圖像的隨機(jī)紋理和瑕疵等可看作噪聲使用字典學(xué)習(xí)算法進(jìn)行去除，因此將字典學(xué)習(xí)用于機(jī)織物紋理表征具有可行性。機(jī)織物圖像屬于結(jié)構(gòu)性的紋理圖像，類似基本的結(jié)構(gòu)單元平鋪而成，顯示出明顯的周期性特征。周建等[5-7]、毛兆華等[8-9]將字典學(xué)習(xí)用于機(jī)織物紋理的近似表達(dá)，在此基礎(chǔ)上開展瑕疵鑒別，取得了相比于傳統(tǒng)的空間域和頻率域瑕疵檢測算法更好的效果，但是他們將字典學(xué)習(xí)用于機(jī)織物表面的瑕疵鑒別時(shí)并沒有考慮織物的組織結(jié)構(gòu)、織物的經(jīng)緯密度、紗線的原料及線密度等結(jié)構(gòu)參數(shù)的變化是否會(huì)對其紋理表征產(chǎn)生影響。而研究這些因素對紋理表征的影響，可對織物紋理進(jìn)行分類，進(jìn)而可探討用同一個(gè)字典表征某一類的織物等問題。本文將主要討論機(jī)織物經(jīng)緯密度對字典表達(dá)紋理的關(guān)系。

1 機(jī)織物紋理表征

1.1 字典學(xué)習(xí)

字典，即一個(gè)m×k矩陣，可通過字典的列線性組合近似得到某一信號。字典D可直接使用預(yù)定義的固定字典，例如小波字典[10]、Gabor字典[11]和離散余弦字典[12]等，另外還可通過選取不同的目標(biāo)函數(shù)進(jìn)行字典學(xué)習(xí)。

字典學(xué)習(xí)可表示為m×n的數(shù)據(jù)矩陣Y，其中m為Y的維數(shù)，n為Y中樣本的個(gè)數(shù)，本文采用最小平方誤差，即選擇l2范數(shù)作為條件進(jìn)行字典學(xué)習(xí)，所尋求的字典可寫成優(yōu)化問題如下。

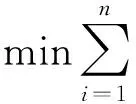
‖yi-Dxi‖2

(1)

對式(1)進(jìn)行最小化，求解字典D，通過該字典的每個(gè)元素的線性組合，實(shí)現(xiàn)對樣本Y的所有元素在最小平方誤差條件下的近似。若D未知，式(1)為非凸優(yōu)化問題，可通過交替迭代法求解。

本文選擇固定的離散余弦字典[13](DCT)作為字典學(xué)習(xí)的初始化字典，再通過字典學(xué)習(xí)算法得到最終的學(xué)習(xí)字典。使用DCT字典的原因包括：1)DCT字典由本身就具有良好的紋理表征能力的離散余弦基所構(gòu)成；2)前人的字典學(xué)習(xí)算法一般都是在確定字典元素的個(gè)數(shù)后隨機(jī)生成一個(gè)初始字典，再求得最終的字典D，這可能導(dǎo)致同一樣本經(jīng)算法學(xué)習(xí)得到的字典不唯一，而固定的初始字典可解決以上問題。實(shí)驗(yàn)發(fā)現(xiàn)，使用DCT字典作為字典學(xué)習(xí)的初始字典不會(huì)對最終學(xué)習(xí)字典重構(gòu)誤差產(chǎn)生影響。

1.2 重構(gòu)圖像評價(jià)指標(biāo)

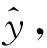
(2)

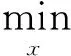
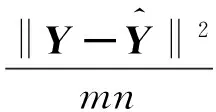
(3)

2 織物制樣與測試

本文實(shí)驗(yàn)所用的機(jī)織物樣本是在實(shí)驗(yàn)室TNY101B-20型櫻牌劍桿小樣織機(jī)上織制的，使用18.22 tex的棉精梳紗為原料，除密度存在變化外，其他條件均相同。共5塊平紋織物和5塊斜紋織物，其中斜紋樣本組織均為二上一下，具體參數(shù)見表1、2。從表中可知：1到5號平紋織物的經(jīng)緯密都是逐漸增大的；I到V號斜紋織物的經(jīng)緯密也是逐漸增大的。

使用佳能9000F MarkII型掃描儀采集織物圖像，采用照片掃描模式，色彩模式為灰度。本文圖像采集所用分辨率為600 dpi，其目的是讓每根紗線直徑在圖像中至少有3個(gè)像素表示，以更好地表征織物的紋理結(jié)構(gòu)。掃描圖像時(shí)織物的橫向和縱向不產(chǎn)生偏斜。為增加圖像的對比度，掃描圖像時(shí)在織物的背面放置一塊全黑的硬紙板作為背景，每張圖像大小為256像素×256像素。

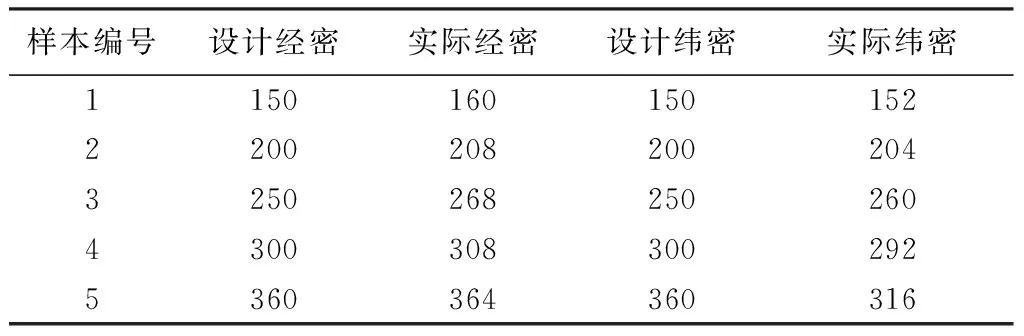
表1 平紋織物規(guī)格Tab.1 Specifications of plain weave fabric 根/10 cm

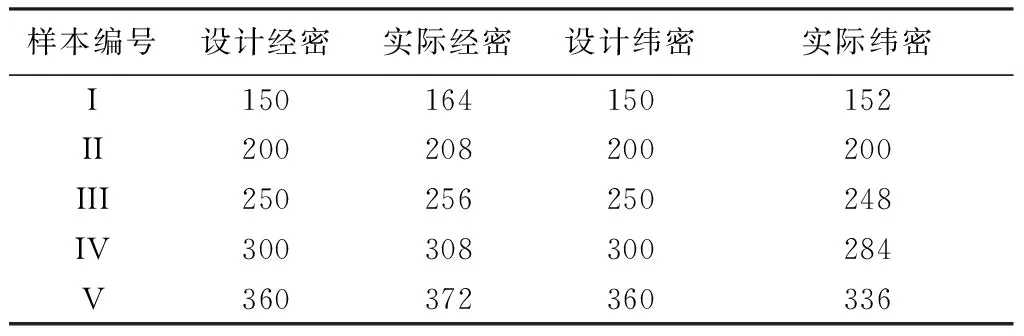
表2 斜紋織物規(guī)格Tab.2 Specifications of twill weave fabric 根/10 cm

重構(gòu)紋理圖像時(shí)，將每幅圖像用16像素×16像素的滑動(dòng)子窗口劃分，一幅256像素×256像素的圖像經(jīng)過劃分得到58 081個(gè)子樣本，使用字典學(xué)習(xí)算法對這58 081個(gè)子樣本進(jìn)行學(xué)習(xí)，得到學(xué)習(xí)字典，并使用學(xué)習(xí)字典重構(gòu)這些子樣本。最后，按子樣本劃分的逆過程疊加融合得到重構(gòu)的紋理圖像。

3 字典學(xué)習(xí)處理與分析

3.1 圖像灰度值分布對重構(gòu)誤差的影響

在討論織物密度變化前，首先討論了圖像灰度值分布對重構(gòu)誤差的影響。灰度直方圖是關(guān)于灰度級分布的函數(shù)，是對圖像中灰度級分布的統(tǒng)計(jì)。一幅數(shù)字圖像在[0,G]范圍內(nèi)共有L個(gè)灰度級，其直方圖定義為以下離散函數(shù)。

h(rk)=nk

(4)

式中：rk為區(qū)間[0,G]內(nèi)的第k級灰度；nk為圖像中rk灰度級的像素?cái)?shù)。在字典學(xué)習(xí)中，圖像數(shù)據(jù)的灰度值分布會(huì)對重構(gòu)誤差產(chǎn)生顯著的影響。

以一幅工廠織制的平紋圖像為樣本，討論灰度值分布對重構(gòu)誤差的影響。圖1(a)示出256像素×256像素的平紋圖像，圖1(b)～(d)分別示出圖1(a)灰度值進(jìn)行線性拉伸變換的結(jié)果。其中，圖1(b)示出對圖1(a)像素值拉伸到0～255范圍后的圖像，圖1(c)示出將圖1(b)的灰度值整體除以3后得到的圖像，圖1(d)示出將圖1(c)的灰度值整體加100所得的圖像，第2行為各圖對應(yīng)的灰度值分布圖。

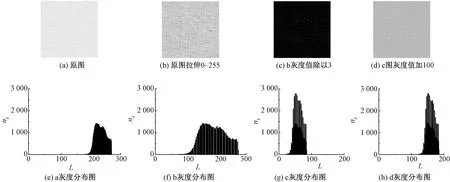
圖1 織物圖像及其灰度分布直方圖Fig.1 Fabric images and their gray distribution histograms. (a)Origin image; (b)0-255 stretch of (a); (c)Gray value of (b) divided by 3; (d)Gray value of (c) plus 100; (e)Gray distribution of (a); (f) Gray distribution of (b); (g) Gray distribution of (c); (h) Gray distrbution of (d)

對圖1中(a)～(d)使用字典學(xué)習(xí)算法重構(gòu)所得均方誤差值如表3所示。由圖1和表3中圖1(a)和圖1(b)結(jié)果可發(fā)現(xiàn)，灰度值的分布越集中，則由字典學(xué)習(xí)后重構(gòu)圖像的誤差越小；比較圖1(b)、(c)和(d)可發(fā)現(xiàn)，對圖像數(shù)據(jù)除以某個(gè)定值s，則經(jīng)字典學(xué)習(xí)后重構(gòu)圖像的誤差約為原來的s-2；對圖像數(shù)據(jù)灰度值整體加某一定值t，只會(huì)改變圖像的亮度，但不會(huì)對重構(gòu)的誤差造成影響。由此可知，圖像的灰度值分布越廣泛，則相同字典個(gè)數(shù)下經(jīng)字典學(xué)習(xí)得到的圖像重構(gòu)誤差越大。

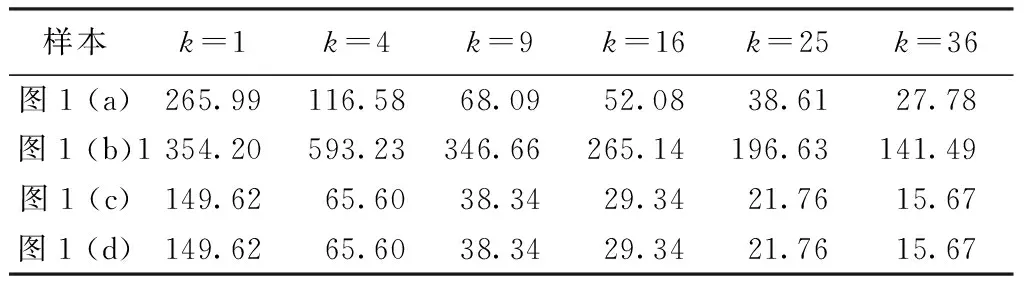
表3 織物圖像在不同原子個(gè)數(shù)下的重構(gòu)誤差Tab.3 Reconstruction error of different fabric images with different atomic numbers

3.2 織物經(jīng)緯密對圖像灰度值分布的影響

由于紗線在圖像中顯示為高灰度值的白色，背景為低灰度值的黑灰色，可推測隨著織物密度的增加，圖像的灰度值分布會(huì)向高灰度值部分集中。以1號和5號平紋織物為例對此進(jìn)行驗(yàn)證，結(jié)果如圖2所示。

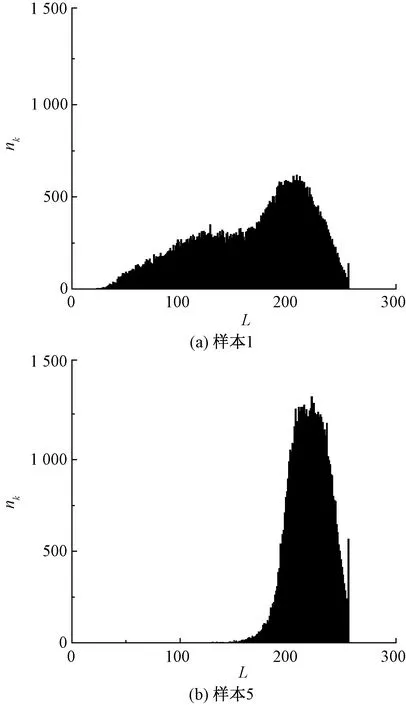
圖2 平紋1號樣本和5號樣本灰度分布圖Fig.2 Gray histograms of plain weave. (a) Sample 1; (b) Sample 5

由圖2可知，1號低密度的平紋樣本灰度值分布更廣泛，而5號高密度平紋樣本的灰度值分布更集中。這是因?yàn)榻?jīng)緯密度增加，會(huì)導(dǎo)致紗線間的間隙變小。間隙部分在圖像中顯示為低亮度黑色背景，紗線部分在圖像中顯示為高亮度白色，因此，隨著織物密度變大，織物圖像的灰度值分布向高亮度像素值部分集中。由此產(chǎn)生圖像灰度值標(biāo)準(zhǔn)不統(tǒng)一，這會(huì)對使用均方誤差作為評價(jià)指標(biāo)的結(jié)果產(chǎn)生影響。

3.3 圖像灰度值標(biāo)準(zhǔn)化處理

為避免因數(shù)據(jù)標(biāo)準(zhǔn)不統(tǒng)一而產(chǎn)生的影響，使用在標(biāo)準(zhǔn)差標(biāo)準(zhǔn)化的基礎(chǔ)上改進(jìn)的方法對圖像灰度值進(jìn)行標(biāo)準(zhǔn)化處理，目的是使圖像的灰度值處于同一水平下，其定義如下。

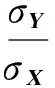
(5)

式中：X和Y分別為原圖像和預(yù)處理之后的圖像灰度值矩陣；μX、μY、σX、σY分別為X和Y的均值和標(biāo)準(zhǔn)差，經(jīng)過預(yù)處理后的織物圖像灰度值具有統(tǒng)一的均值μY和標(biāo)準(zhǔn)差σY。選取合適的均值和標(biāo)準(zhǔn)差可使預(yù)處理后的圖像灰度值盡可能分布于0～255之間。

4 實(shí)驗(yàn)結(jié)果與分析

4.1 字典個(gè)數(shù)對重構(gòu)誤差的影響

以平紋樣本1為例，驗(yàn)證字典個(gè)數(shù)對重構(gòu)誤差的影響，分別初始化DCT原子的個(gè)數(shù)k為1、4、9、16、25、36，進(jìn)行重構(gòu)實(shí)驗(yàn)，結(jié)果如圖3所示。

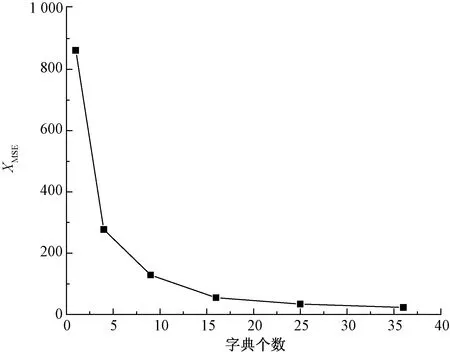
圖3 均方誤差隨字典個(gè)數(shù)變化曲線Fig.3 XMSE change with dictionary numbers

由圖3可知，隨著初始字典元素個(gè)數(shù)的增加，重構(gòu)圖像的均方誤差值先顯著減小而后趨于平緩。當(dāng)字典個(gè)數(shù)超過9時(shí)，均方誤差值減小已不明顯。此時(shí)若繼續(xù)增加字典的個(gè)數(shù)，一方面增加算法運(yùn)行時(shí)間，另一方面只是進(jìn)一步完善重構(gòu)圖像的隨機(jī)紋理信息，而隨機(jī)紋理在機(jī)織物紋理研究中不需要，因此取本文初始化DCT字典原子個(gè)數(shù)k=9進(jìn)行下一步實(shí)驗(yàn)。

4.2 織物密度對重構(gòu)誤差的影響

為探討織物密度對重構(gòu)誤差的影響，將不同密度的樣本代入式(1)定義的字典學(xué)習(xí)算法，初始化DCT原子的個(gè)數(shù)為k=9，對樣本進(jìn)行子窗口樣本劃分，代入字典學(xué)習(xí)算法并獲得重構(gòu)圖像。圖4分別示出表1中平紋和表2中斜紋織物樣本原圖及其在k=9條件下重構(gòu)的圖像。比較重構(gòu)圖像和原圖像可發(fā)現(xiàn)，重構(gòu)圖像保留了原圖的絕大部分紋理，但丟失了一些隨機(jī)紋理，如5號樣本的重構(gòu)結(jié)果所示。

圖4 機(jī)織物樣本及其重構(gòu)圖像Fig.4 Origin images of sample 1(a), 2(b), 3(c), 4(d), 5(e), I(f), II(g), III(h), IV(i), and V(j), and reconstructed images of sample 1(k), 2(l), 3(m), 4(n), 5(o), I(p), II(q), III(r), IV(s), and V(t)

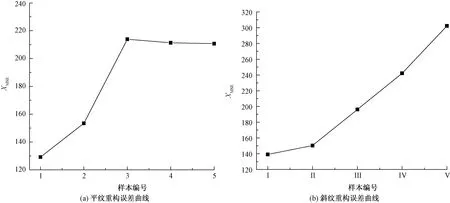
圖5 不同密度織物重構(gòu)圖像均方誤差關(guān)系圖Fig.5 Mean square error curves of reconstructed images with different densities. (a) Samples 1-5; (b) Samples I -V

根據(jù)式(3)計(jì)算得到的均方誤差和樣本密度的關(guān)系如圖5所示。

由圖5(a)可知，對于平紋織物，隨著織物密度的增大，重構(gòu)圖像的均方誤差先增大而后略有減小，基本趨于不變。說明隨著織物密度的增大，在本文所制樣本密度150～360根/10 cm范圍內(nèi)，平紋重構(gòu)圖像的質(zhì)量變差，達(dá)到一定密度后不再顯著變化。由圖5(b)可知，對于斜紋樣本，隨織物密度的增大，重構(gòu)圖像的均方誤差逐漸增大。說明隨密度增加，在本文所制樣本密度150～360根/10 cm范圍內(nèi)，斜紋重構(gòu)圖像的質(zhì)量變差。超出本文樣本的密度范圍，斜紋紋理圖像的重構(gòu)誤差可能像平紋一樣不再顯著增大，結(jié)果需要進(jìn)一步實(shí)驗(yàn)驗(yàn)證。

將圖5中相同密度的平紋和斜紋進(jìn)行比較可發(fā)現(xiàn)，斜紋紋理的重構(gòu)誤差大于平紋，同時(shí)平紋和斜紋重構(gòu)圖像的均方誤差隨密度變化曲線也存在差異，說明組織結(jié)構(gòu)也會(huì)對字典重構(gòu)紋理圖像的質(zhì)量產(chǎn)生顯著的影響。

5 結(jié) 語

本文使用DCT字典作為字典學(xué)習(xí)的初始字典用于機(jī)織物圖像的紋理表征，首先討論了織物圖像灰度值分布對字典學(xué)習(xí)重構(gòu)圖像誤差的影響，得出在一定字典個(gè)數(shù)條件下，織物圖像的灰度值分布越集中則重構(gòu)誤差越小的結(jié)論。在此基礎(chǔ)上，對樣本圖像的灰度值進(jìn)行標(biāo)準(zhǔn)化處理，將圖像灰度值拉伸到同一水平后，將不同密度的平紋和斜紋應(yīng)用本文的字典學(xué)習(xí)算法進(jìn)行實(shí)驗(yàn)，并討論織物密度對字典學(xué)習(xí)重構(gòu)織物紋理圖像質(zhì)量的影響。實(shí)驗(yàn)發(fā)現(xiàn)，當(dāng)字典個(gè)數(shù)k=9時(shí)，在本文織制的經(jīng)緯密度150～360根/10 cm范圍內(nèi)，隨著織物密度的增大，平紋重構(gòu)圖像與原圖像的誤差先變大而后趨于不變，斜紋重構(gòu)圖像與原圖像的誤差隨織物密度的增大而增大。超出本文實(shí)驗(yàn)密度范圍的重構(gòu)結(jié)果需進(jìn)一步驗(yàn)證。

FZXB

[1] 薛樂. 基于傅里葉變換和Gabor變換的機(jī)織物紋理分析方法研究[D]. 上海：東華大學(xué), 2015:16-32. XUE Le. Study on woven fabric texture based on fourier transform and gabor transform[D]. Shanghai: Donghua University,2015:16-32.

[2] 姚芳. 織物紋理的表征和自動(dòng)識(shí)別的研究[D]. 上海：東華大學(xué), 2010:20-40. YAO Fang. Study on fabric texture representation and automatic identification[D]. Shanghai: Donghua University,2010: 20-40.

[3] 張軍. 基于局部結(jié)構(gòu)分布的統(tǒng)計(jì)紋理表征方法研究[D].西安：西安電子科技大學(xué),2014:75-91. ZHANG Jun. Statistical texture represention based on the distribution of local structure[D].Xi′an: Xidian University,2014: 75-91.

[4] 張偉偉.圖像紋理特征提取及分類方法研究[D].天津：天津大學(xué),2012:16-43. ZHANG Weiwei.Study of texture feature extraction and classification method[D].Tianjin: Tianjin University,2012:16-43.

[5] ZHOU Jian, WANG Jun. Fabric defect detection using adaptive dictionaries[J]. Textile Research Journal, 2013,83(17):1846-1859.

[6] 周建.基于字典學(xué)習(xí)的機(jī)織物瑕疵自動(dòng)檢測研究[D].上海：東華大學(xué),2014:29-42. ZHOU Jian. Automated woven fabric defect detection using dictionary learning[D]. Shanghai: Donghua University, 2014: 29-42.

[7] ZHOU Jian, SEMENOVICH D, SOWMYA A, et al. Dictionary learning framework for fabric defect detec-tion[J]. Journal of the Textile Institute, 2014, 105(105):223-234.

[8] 毛兆華.基于非負(fù)字典學(xué)習(xí)的機(jī)織物瑕疵檢測算法研究[D].上海：東華大學(xué)，2015:9-32. MAO Zhaohua. Woven fabric defetc detetion based on non-negative dictionary learning[D]. Shanghai: Donghua University, 2015:9-32.

[9] 毛兆華, 汪軍, 周建,等. 應(yīng)用非負(fù)字典學(xué)習(xí)的機(jī)織物瑕疵檢測算法[J]. 紡織學(xué)報(bào), 2016, 37(3):144-149. MAO Zhaohua,WANG Jun,ZHOU Jian,et al.Woven fabric defect detection based on non-negative dictionary learning[J].Journal of Textile Research, 2016, 37(3):144-149.

[10] 田莉萍,王建國.基于小波字典稀疏表示的SAR圖像目標(biāo)識(shí)別[J].雷達(dá)科學(xué)與技術(shù), 2014(1): 44-50. TIAN Liping, WANG Jianguo. Target recongnition of SAR images based on sparse representation of wavelet dictionary[J]. Radar Science and Techonology, 2014(1): 44-50.

[11] 曾軍英, 甘俊英, 翟懿奎. Gabor字典及l(fā)0范數(shù)快速稀疏表示的人臉識(shí)別算法[J]. 信號處理, 2013,29(2):256-261. ZENG Junying, GAN Junying, ZHAI Yikui. Face recognition based on fast sparse representation of Gabor dictionary andl0norm[J].Journal of Siganal Processing, 2013, 29(2):256-261.

[12] ELAD M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Proces-sing[M]. New York: Springer, 2010: 235-237.

[13] 劉艷,李宏東.DCT域圖象處理和特征提取技術(shù)[J].中國圖象圖形學(xué)報(bào), 2003, 8(2):121-128. LIU Yan, LI Hongdong. Image and video processing techniques in the DCT domain[J]. Journal of Image and Graphics, 2003, 8(2):121-128.

Influence of woven fabric density on texture representation based on dictionary learning

WANG Kai1，WU Ying1，ZHOU Jian2，WANG Jun1,3，LI Liqing1

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.CollegeofTextilesandClothing,JiangnanUniversity,Wuxi,Jiangsu214122,China; 3.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)

In order to discuss an smart evaluation method for objective evaluation on fabric appearance quality, patches extracted from woven fabric images with different densities were used as training samples and discrete cosine dictionary was used as the initial dictionary of learning algorithm based on the least square method. The original woven fabric image samples can be reconstructed well by the dictionary by a linear summation of its elements. To evaluate the reconstruction performance, mean square error was selected as evaluation index. The influence of gray distribution of fabric images on the reconstruction error was discussed, and then the influences of density on the reconstruction error were discussed with the normalized image gray value. The experimental results show that when the number of dictionary atoms equals to 9, the mean square error of plain increases firstly and then remains within a certain range and the mean square error of twill increases with the increasing of warp and weft density from 150 to 360 yarns/10 cm.

dictionary learning; woven fabric; texture representation; density

10.13475/j.fzxb.20160800606

2016-08-03

2017-02-21

國家自然科學(xué)基金項(xiàng)目(61379011, 61501209, 61271006)

王凱(1992—)，男，碩士生。主要研究方向?yàn)闄C(jī)織物紋理表征。汪軍，通信作者，E-mail：junwang@dhu.edu.cn。

TS 101.9

A