衛星姿態四元數的連續化方法及姿態控制算法研究

劉善伍 陳宏宇 張學鋼

上海微小衛星工程中心 ,上海 200050

衛星姿態四元數的連續化方法及姿態控制算法研究

劉善伍 陳宏宇 張學鋼

上海微小衛星工程中心 ,上海 200050

對無陀螺的微小衛星，提出了一種僅利用磁強計、太陽敏感器作為定姿部件的改進雙矢量定姿算法，該算法解決了四元數輸出跳變問題，基于該定姿算法確定的連續四元數設計了具有濾波功能的衛星姿態控制算法。仿真結果表明，該算法可保障衛星在任意初始狀態下的姿態穩定，提高了可靠性、安全性，具有良好的工程應用前景。 關鍵詞 姿態確定；姿態控制；四元數；微小衛星

對于以中等精度、低成本和小型化為目標的低軌微小衛星來說，以太陽敏感器、磁強計為主組成的姿控系統以其可靠性高、重量輕和功耗低的優點受到廣泛關注。國內外許多文章均對此做了闡述，其中，大量的研究集中在衛星姿態角速率信息能通過陀螺等慣性部件直接測量，或通過EKF和UKF等[1-2]估計得到的情況下，采用滑模控制、反饋線性化及LQR等多種方法均能得到理想的控制效果[3-8]。但是在衛星初始入軌階段，需要進行全姿態捕獲時，如果衛星姿態角速率信息無法直接獲取，而雙矢量定姿等給出的四元數信息中的標量一般定義為正，在衛星翻滾過程中，定姿得到的四元數信息出現跳變，無法從四元數直接解算角速率信息，導致姿態控制律設計困難。

本文以某型號衛星為研究背景，提出一種工程實用的改進四元數算法，使得從姿態矩陣解算的四元數連續，確保所有情況下都可以直接從四元數信息中獲得角速率信息，并設計了改進的PD控制律，引入低通濾波器以增強控制器對系統噪聲的抑制能力，提高了衛星姿態控制的動態性能。

1 研究對象

運動在極軌近圓形軌道上，不含動量部件的衛星動力學及運動學方程[9]為：

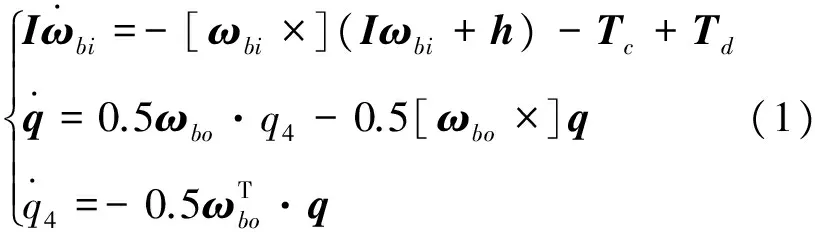
2 改進的雙矢量定姿算法

在已知參考坐標系中能得到2個互不平行的矢量，可采用雙矢量定姿確定衛星的三軸姿態，常用的雙矢量定姿方法有TRIAD算法[10]和QUEST算法[11]

等。本文在經典TRIAD算法基礎上，提出一種改進的四元數算法，使得衛星即使在大姿態翻滾的情況下，從姿態矩陣解算的四元數依然保持連續。

2.1TRIAD算法

由磁強計測得衛星本體系磁矢量Bb，太陽敏感器測得本體系太陽矢量Sb，并通過星載磁場表及太陽軌道模型得到軌道系下的磁矢量Bo及太陽矢量So。

定義軌道系到本體系的轉換矩陣為R，顯然有N=RM，則：R=NM-1。

至此，得到軌道系與本體系的轉移矩陣為R，可用四元數表示為:

由姿態轉移矩陣解算四元數的基本方法為：

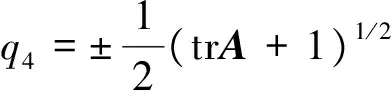
(2)

式中，trA為求A的跡。

2.2 改進的四元數求解算法

當衛星大姿態翻滾時，式(2)中的標量q4可能為0，導致四元數無法正常提取。PSS(普林斯頓衛星系統)SCT(空間飛行器控制工具箱)中針對該問題提出了一種解算方法，解決了該問題。算法中，強制取標量q4≥0，當衛星大姿態翻滾時，四元數可能發生跳變，不利于控制律的設計。針對該問題，本文提出了一種改進的方法，首先定義四維向量：

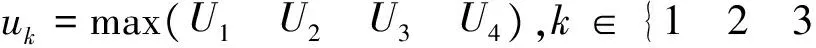
4},得到相應U向量的下角標k值。

根據得到的k值，首先解算qk：

qk=sign(qk_last)(1+2Rkk-trR)1/2/2， (k=1，2，3),q4=sign(q4_last)(1+trR)1/2/2， (k=4)。

其中，qk_last為前一時刻計算得到的qk。

再由qk求解其他各值，至此得到連續四元數解算算法如下：

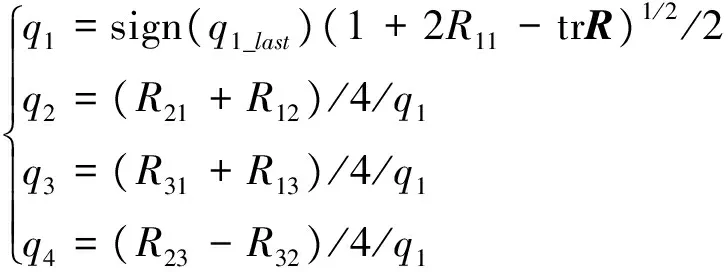
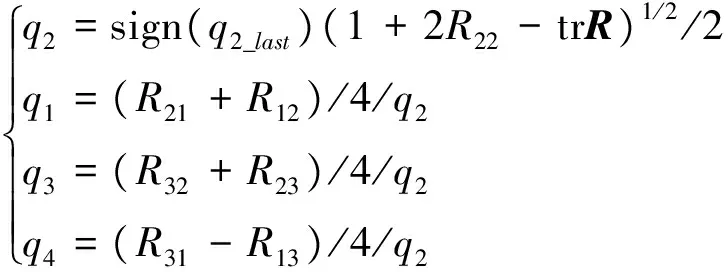
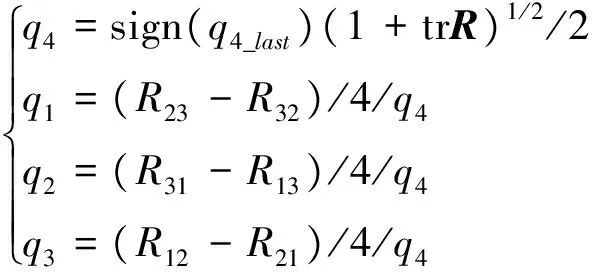
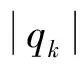
3 姿態控制算法設計

3.1 四元數解算ωbo的PD控制律

由式(1)可知：

即ωbo可由下式求得：

(3)

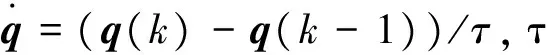
于是，得到衛星姿態控制律為：

Tcdes=kpq+kdωbo

(4)

3.2 控制律修正

由于式(3)中包含微分項，對高頻系統噪聲非常敏感，因此控制律中引入濾波環節，即，

(5)

其中，τf為濾波環節的時間常數。

4 仿真結果

某型號衛星運行軌道為：軌道高度為400km，偏心率為0，軌道傾角為42°。

衛星的慣量陣：

以磁強計、太陽敏感器作為姿態測量部件，反作用飛輪作為主動控制部件。定姿算法采用TRIAD算法及改進的四元數求解算法，姿態控制采用基于連續四元數的PD控制律,控制律選用式(5)。

控制系數選取如下：

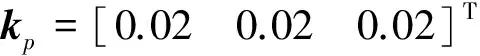
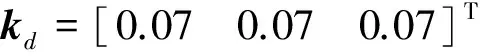
τf=0.5s，τ=0.5s。

仿真干擾情況： 1)磁強計測量噪聲均值為0，方差為500nT2；2)太陽敏感器噪聲均值為0，方差為1mA2。

通過Matlab/Simulink進行仿真，圖1～2給出以下2種不同初始條件下的姿態控制仿真曲線：

1)仿真初始條件1：

2)仿真初始條件2：

圖1 初始條件1下仿真曲線

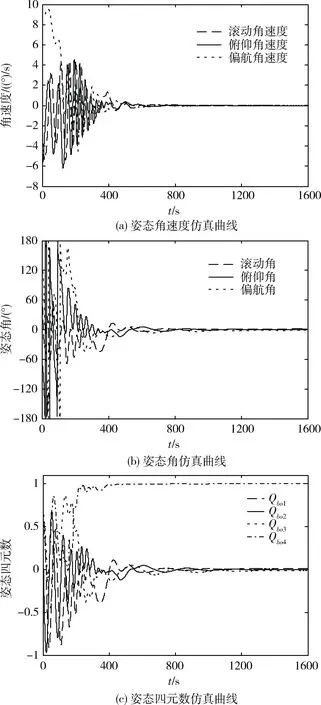
圖2 初始條件2下仿真曲線

從以上2種仿真曲線上可以看到，即使在很大初始角速度下，衛星姿態出現大幅度翻滾，姿態角出現奇異，但姿態四元數依舊平滑收斂，相比小初始條件的情況，只是收斂時間變長，說明了本文所采用的四元數連續化方法有效，避免了四元數的調變問題。

5 結論

研究了衛星四元數的連續化輸出問題，避免了在衛星入軌初期或由于故障導致姿態失控后，姿態角及角速率較大情況下采用常規的TRIAD和QUEST等雙矢量定姿方法確定的四元數標量項一般取正而導致的四元數出現調變的缺點。此外，還基于連續化的姿態四元數設計了具有濾波功能的姿態控制律。仿真驗證該算法有效，具有較高的可靠性及安全性，有良好的工程應用前景。

[1] 張銳，朱振才，張靜，朱光沂.基于磁強計的微小衛星姿態確定[J].宇航學報， 2006, 27(4): 578-581. (ZhangRui,ZhuZhencai,ZhangJing，etal.Micro-SatelliteAttitudeDeterminationBasedonMagnetometer[J].JournalofAstronautics, 2006, 27(4): 578-581.)

[2] 劉海穎，王惠南，程月華. 純磁控微小衛星姿態控制研究[J].空間科學學報,2007，27(5):425-429. (LiuHaiying,WangHuinan,ChengYuehua.AttitudeControlofMicro-SatellitewithOnlyMagneticActuators[J].SpaceScience, 2007，27(5): 425-429.)

[3] 楊寧寧,楊照華,余遠金.基于機械飛輪干擾補償的小衛星自適應滑模變結構姿態控制[J].航天控制, 2013,(1):51-57.(YangNingning,YangZhaohua,YuYuanjin.TheSmallSatelliteAdaptiveSlidingModeAttitudeControllerwithMechanicalFlywheelsDisturbanceCompensation[J].AerospaceControl, 2013,(1):51-57.)

[4]LoSC,ChenYP.SmoothSliding-modeControlfor

Spacecraft Attitude Tracking Maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(6): 1345-1349.

[5] Shtessel Y, Edwards C, Fridman L, et al. Sliding Mode Control and Observation[M]. New York, NY, USA: Birkh?user, 2014.

[6] 郭延寧, 李傳江, 馬廣富. 基于LQR的小衛星磁姿態控制設計[J]. 空間控制技術與應用, 2008, 34(5):61-64. (Guo Yanning, Li Chuanjiang, Ma Guangfu. An LQR-Based Magnetic Attitude Control Design for Small Satellite[J]. Aerospace Control and Application, 2008, 34(5):61-64 .)

[7] Bryson Jr A E. Control of Spacecraft and Aircraft [M]. Princeton University Press, 2015.

[8] Horri N M, Palmer P, Hodgart S. Practical Implementation of Attitude-control Algorithms for an Underactuated Satellite [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 40-45.

[9] 章仁為.衛星軌道姿態動力學與控制[M]. 北京航空航天大學出版社，1998:147-153.

[10] Shuster M D, OH S D. Three-axis Attitude Determination from Vector Observations[J]. Journal of Guidance Control, and Dynamics, 1981, 4(1): 70-77.

[11] Shuster M D. The Quest for Better Attitudes [J]. The Journal of the Astronautical Sciences, 2006, 54(3):657-683.

The Algorithm of Continuous Quaternion and Attitude Control of Satellite

Liu Shanwu, Chen Hongyu, Zhang Xuegang

Shanghai Engineering Center for Micro-satellite, Shanghai 200050, China

Themodifiedattitudedeterminationalgorithmwithonlysunsensorandmagnetometerforsatellitewithoutgyroisproposed.Thisalgorithmsolvestheproblemofun-sequentialquaternion,andattitudecontrolalgorithmwithfilterbasedsequentialquaternionisdesigned.Thesimulationresultsindicatethatattitudeisstableandefficientlyadjustedbyusingthecontrolmethodproposed,whateverinitialstateis,anditgreatlyimprovethereliabilityofsatellite.Itpromisesthefairgoodapplicationinengineering.

Attitudedetermination;Attitudecontrol;Quaternion;Micro-satellite

2017-02-17

劉善伍(1982-)，男，吉林農安人，碩士，主要研究方向為衛星控制系統設計；陳宏宇(1976-)，男，山西大同人，博士，主要研究方向為衛星總體設計、控制系統設計；張學鋼(1990-)，男，安徽蚌埠人，博士研究生，主要研究方向為衛星控制系統設計。

V412

A

1006-3242(2017)03-0030-04