基于有限元分析內部裂紋對球軸承外圈振動特征的影響
葉九龍, 張杰
(1.成都工業職業技術學院 汽車工程系,成都 610061;2.西南交通大學 牽引動力國家重點實驗室,成都 610031)
滾動軸承在航空航天、機械裝備等領域廣泛應用[1]。在交變載荷下,軸承套圈易出現表面裂紋和內部裂紋[2]。當出現表面裂紋和內部裂紋時,套圈局部剛度改變,會影響其結構的模態參數和振動特征[2],故可通過監測結構剛度的變化實現對軸承套圈損傷的檢測。
通過開展裂紋引起的軸承套圈振動特征變化的研究,可診斷和識別套圈的裂紋失效形式。國內外學者進行了大量研究,文獻[1]推導了圓環彎扭振動的表達式,計算了不同邊界條件的圓環特征值;文獻[3]研究了軸對稱圓環的平面彎曲振動特征,得到圓環面內彎曲振動的固有表達式。若選取合適的軸承套圈參數時,軸承套圈存在頻率接近為0的近似正交模態;文獻[4]研究了軸向極化壓電陶瓷薄圓環的徑向振動特征,推導了其機電等效電路,獲得了圓環振子的共振與反共振頻率方程,并對其結果進行了試驗驗證;文獻[5]采用有限元法對系列均質平面圓環的振動特征進行了分析,研究了疊層平面圓環的振動特征以及疊層對其振動的影響,并進行試驗研究;文獻[6]基于有限元法仿真分析了圓環的諧振頻率;文獻[7]研究了正常圓環和圓環梁結構的自由振動特征。
大多數研究主要集中在正常軸承套圈的振動特征[1-12],而對裂紋引起的軸承外圈的振動特征變化研究較少,尤其是內部裂紋引起的振動特征變化。鑒于此,以含內部裂紋的軸承外圈為研究對象,基于有限元法建立正常軸承外圈和含內部裂紋軸承外圈的有限元模型,仿真分析內部裂紋對外圈固有頻率、模態振型及模態振型曲率的影響。
1 理論分析
1.1 球軸承外圈的振動特征
自由支承條件下,軸承外圈存在徑向和軸向彎曲振動,徑向彎曲振動的n-1階固有頻率為[12]
(1)
式中:n為固有頻率的階次;E為彈性模量;ρ為密度;S為橫截面積;Ia為截面慣性矩;R為中徑半徑。
基于有限元法的軸承外圈自由模態仿真分析,首先采用有限元法對外圈進行單元離散,再構建外圈的數學模型,求解外圈的特征值與特征向量,得到的特征值為外圈的固有頻率,特征向量為外圈的振型。
以廣義坐標x描述n個自由度的受迫振動系統,在外載荷的作用下,通過動力學理論得到外圈的運動微分方程為[11]

(2)

模態分析為軸承外圈的固有特性,與所受外載荷無關,且在求解外圈的固有特性時,阻尼對外圈的固有特性影響較小。故(2)式轉化為[11]

(3)
令
x=Asinω(t-t0),
(4)
式中:A為第n階位移向量x的幅值向量,即振型;ω為與向量A對應的自然頻率;t為時間;t0為初始條件確定的時間常數。
將(4)式代入(3)式得系統的廣義坐標方程為
(K-ω2M)A=0,
(5)
1.2 球軸承外圈模態振型曲率[13-14]
假設通過有限元法得到軸承外圈的模態振型矢量為φ,根據差分原理,計算外圈的曲率模態矩陣,令Sij為矩陣φ的元素,則外圈的曲率模態矩陣為
(6)
式中:i為外圈有限元模型的節點號,i= 1,2,…,n;j為模態頻率的階次,j=1,2,…,6 ;li為外圈有限元模型的單元長度。
2 模型建立
正常軸承外圈如圖1所示,R1為外圈內半徑,R2為外圈外半徑,T為厚度。含內部裂紋的軸承結構如圖2所示,L為裂紋的長度,H2為寬度,H1為裂紋下表面距離軸承外圈內表面的距離,該裂紋為軸向內部裂紋。裂紋尖端區域有限元模型如圖3所示。為準確描述裂紋特性,對裂紋尖端區域采用奇異單元進行離散。為簡化有限元模型,假設軸承外圈為理想圓環結構,但要保證其彈性模量、密度、橫截面積、截面慣性矩和中徑半徑與理論模型一致。為減少計算和提高計算精度,對正常外圈和含內部裂紋外圈的有限元模型采用高質量的四邊形殼平面應變單元進行網格劃分,以滿足計算精度要求。軸承外圈整體有限元的單元總數為10 560,節點總數為11 220。球軸承外圈的兩端面為自由端面或被剛性光滑面所固定,不發生縱向位移,采用二維平面應變單元對外圈建模[15]。

圖1 正常軸承外圈
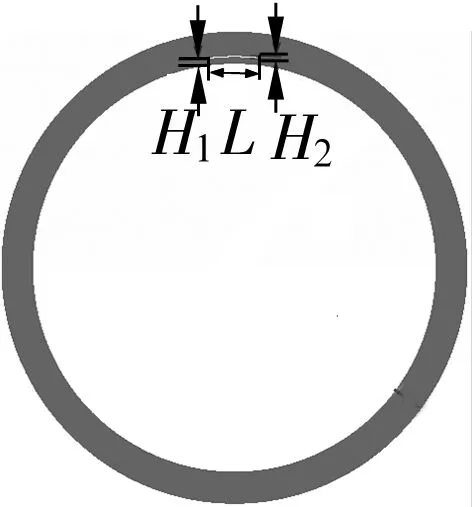
圖2 含裂紋軸承外圈

圖3 裂紋尖端模型
選取R1為62.5 mm,R2為72 mm,T為19 mm,L為8 mm,H2為0.3 mm,H1為1 mm。軸承外圈材料為GCr15鋼,彈性模量為210 GPa,密度為7 800 kg/m3,泊松比為0.3。
3 結果與分析
通過有限元法對正常軸承外圈和含內部裂紋的軸承外圈進行自由模態分析[16],提取前6階固有頻率和模態振型及其曲率進行分析。正常和含內部裂紋的軸承外圈固有頻率見表1。通過(1)式得到軸承外圈的前6階頻率分別為2 610,7 300,13 230,20 670,29 896,39 670 Hz。由表1可以看出,有限元法和理論計算法計算基本一致,說明有限元法的模型正確。
由表1可知,內部裂紋使軸承外圈的前6階固有頻率減小,但減小幅度降低,僅通過固有頻率的變化對外圈的內部裂紋進行診斷和識別比較困難。

表1 有限元分析結果
正常和含內部裂紋軸承外圈的前6階模態振型分別如圖4和圖5所示。由圖可知,內部裂紋對外圈模態振型的整體形態影響較小,由于裂紋區域局部剛度變化,在裂紋區域引起的局部模態變化較為明顯。前6階模態中,裂紋存在閉合和張開2種模態振型;第1,2和3階,裂紋區域為閉合模態振型;第4,5和6階,存在閉合和張開2種模態振型。

圖4 正常軸承外圈模態振型
含內部裂紋軸承外圈前6階模態振型曲率如圖6所示,由圖可知,正常軸承外圈模態振型曲率(曲線1)為光滑曲線,而含內部裂紋的軸承外圈模態振型曲率(曲線2)在裂紋區域存在明顯的突變現象。內部裂紋會對外圈模態振型曲率產生較大的影響,且其影響區域即為裂紋所在的區域,故可通過診斷和識別外圈模態振型的曲率得到內部裂紋所在位置。
由于模態振型存在特殊節點,即振幅為0的節點,模態振型曲率可能出現對于特殊節點或其他影響而導致無突變的情況。內部裂紋長度對軸承外圈第4階模態振動曲率的影響如圖7所示。3種裂紋工況的高度和深度分別為0.3,1 mm。由圖7可知,對于不同長度尺寸的內部裂紋,模態曲率方法也同樣適用。

圖5 含內部裂紋軸承外圈模態振型

圖6 軸承外圈模態振型曲率
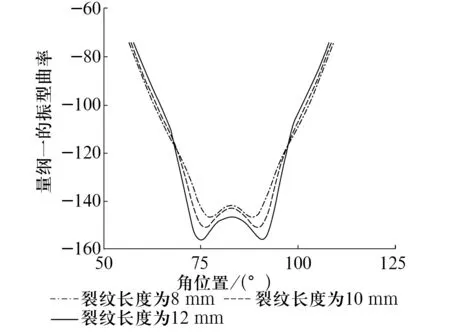
圖7 內部裂紋長度對軸承外圈第4階模態振型曲率的影響
4 結論
1)內部裂紋會使軸承外圈固有頻率減小,但減小幅度較小;只采用固有頻率的變化對外圈的內部裂紋進行診斷和識別比較困難。
2)內部裂紋對軸承外圈模態振型的整體形態影響較小,但在裂紋存在的區域引起的局部模態變化較為明顯。
3)內部裂紋對外圈模態振型曲率有較大影響,影響區域即為裂紋所在區域,可通過分析外圈模態振型的曲率來診斷和識別內部裂紋所在位置。

