基于相關峭度準則EEMD及改進形態濾波的軸承故障診斷方法

李翠省，劉永強，廖英英

(石家莊鐵道大學 a.機械工程學院；b.土木工程學院， 石家莊 050043 )

滾動軸承運行工況復雜，早期的微弱故障信號常被強噪聲嚴重污染，造成故障特征提取困難，因此，抑制噪聲、提取故障特征是軸承故障診斷的研究熱點。成熟的小波分析雖然具有多分辨率等優點，但消噪效果很大程度上依賴于閾值和基函數的選擇，缺乏自適應性[1-2]；集成經驗模態分解(Ensemble Empirical Mode Decomposition，EEMD)[3]能夠自適應地將信號從高頻到低頻逐次分解為具有不同振動模式的IMF分量，近些年來被廣泛應用于旋轉機械設備的故障診斷中。

EEMD處理后高頻部分的IMF分量包含較多的故障沖擊成分，但其中仍含有大量噪聲，需進一步對IMF分量進行選取、濾波。文獻[4]將相關峭度(Correlated Kurtosis，CK)應用于SVD分量的選取中，克服了峭度不能反映特定信號特征的缺點，取得了較好效果。形態濾波可以在濾除噪聲的同時最大限度地保留故障信號特征，將形態濾波器用于軸承故障信號的消噪處理[5]，并與EEMD相結合[6]，能夠在抑制噪聲的同時突出故障沖擊成分，在軸承故障診斷中的效果明顯。

基于以上研究成果，將相關峭度準則與EEMD及形態濾波相結合，選取經EEMD處理后相關峭度值最大及次大的IMF分量進行重構，并依據相關峭度值最大原則確定形態學結構元素的長度，以更加有效地提取故障信息特征，獲得更好的診斷效果。

1 基本原理

1.1 集成經驗模態分解

EEMD是針對傳統EMD的不足而提出的一種噪聲輔助信號處理方法，其通過多次在原信號中加入給定幅值的白噪聲并進行EMD處理，從而自適應地將非線性、非平穩信號分解為若干個IMF分量和1個余項r[7]。EEMD利用白噪聲頻譜的均勻分布統計特性，使不同頻帶尺度的信號自動映射到合適的參考尺度上，克服了極值點上下包絡線的擬合誤差，從而有效地避免模態混疊現象，并對多次分解的IMF分量進行疊加求平均處理，達到了消除噪聲影響的目的。

1.2 相關峭度

由于機械設備中的沖擊源很多，EEMD處理后常會出現與原信號無關的分量，僅采用峭度指標衡量軸承故障成分效果明顯不佳。相關峭度[8]同時具備峭度和相關函數的特性，可有效反應振動信號中特定周期脈沖信號強度的參數。軸承故障成分的周期性強，在給定偏移周期的前提下，相關峭度能準確反映感興趣周期脈沖信號的強度，相關峭度值越大，說明其包含的故障沖擊成分越多。

(1)

式中：xn為振動信號；T為感興趣脈沖信號的周期；N為采樣長度；M為偏移周期個數。

1.3 形態濾波器

形態濾波器利用預先設定的結構元素對目標信號進行修正或匹配，很好地保持信號主要形態特征的同時，達到抑制噪聲和提取有用信號的目的。形態學濾波包含膨脹、腐蝕、形態閉、形態開4類基本算子[9]，閉運算能夠抑制或平滑下方的波谷噪聲，開運算能夠濾除信號上方的峰值噪聲[10]。在實際信號中，往往同時存在正負脈沖，為同時發揮開、閉算子的優勢，通常采用形態開、形態閉的級聯形式構造均值濾波器對振動信號去噪，即

(2)

2 軸承故障診斷分析

2.1 優選結構元素長度

結構元素的選取對形態濾波效果的影響很大，其形狀、尺寸要盡可能接近待分析信號的形態特征。結構元素的選取包含結構元素的形狀、高度、長度等。結構元素的形狀對濾波效果影響很小[11]，為了便于計算，選取幅值為0的直線形結構元素，結構元素的形狀、高度確定后，長度的最優解成為了形態濾波的關鍵工作[12-13]。

采用相關峭度準則自適應尋求最優結構元素長度的策略，依據相關峭度指標衡量濾波效果，信號經形態濾波后的相關峭度值越大，說明其中沖擊成分保留越多，濾波效果越好。設定直線形結構元素長度范圍為[2，1倍故障周期長度][12]，結構元素長度從2開始依次增加1個長度間隔直至1倍故障周期長度，計算不同長度所對應的相關峭度值，相關峭度值最大時所對應的結構元素長度即為最優長度，具體流程如圖1所示。

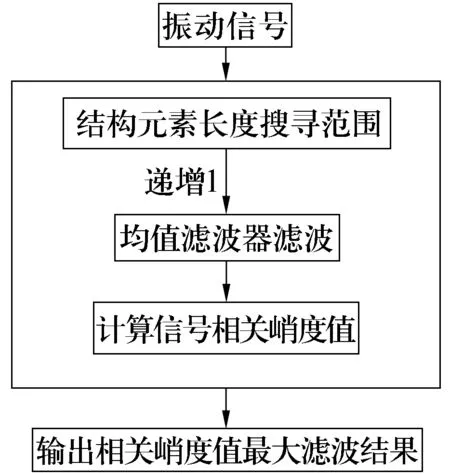
圖1 改進形態濾波流程圖

2.2 特征提取策略

首先，將振動信號進行EEMD處理，計算各IMF分量的相關峭度值，選取相關峭度值最大及次大的IMF分量進行重構，這樣既保留了最多的故障信息,又削弱了強噪聲的干擾；然后，對重構信號進行改進的形態濾波處理，進一步抑制噪聲，提高故障診斷的精度；最后，將濾波后的信號進行Hilbert包絡譜分析。具體流程如圖2所示。

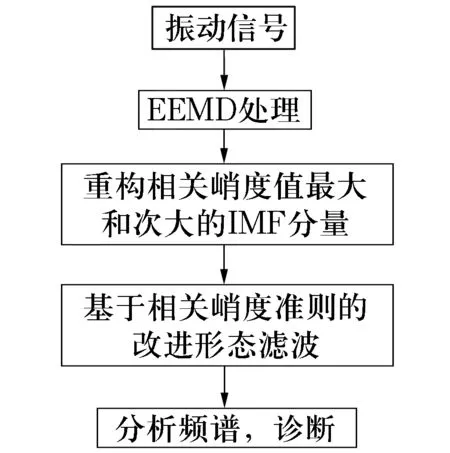
圖2 軸承故障特征提取流程

3 試驗分析

為驗證上述方法的有效性和可行性，在QPZZ-Ⅱ型旋轉機械故障試驗平臺上進行故障模擬試驗。試驗平臺如圖3所示，試驗軸承為6205-2RS型深溝球軸承，其主要參數見表1。用激光在內圈溝道上切割一個邊長0.2 mm、深0.1 mm的正方形凹槽模擬軸承表面損傷類故障，采樣頻率為10 240 Hz，轉速為882 r/min，內圈故障特征頻率fi為79.6 Hz。

圖3 QPZZ-Ⅱ型旋轉機械故障試驗臺

表1 試驗軸承的主要參數

以內圈故障為例進行分析，其振動信號的時域和頻域圖如圖4所示，由于強噪聲的干擾，從時域圖中很難識別故障沖擊成分，頻域圖上亦無法發現故障頻率及其倍頻。

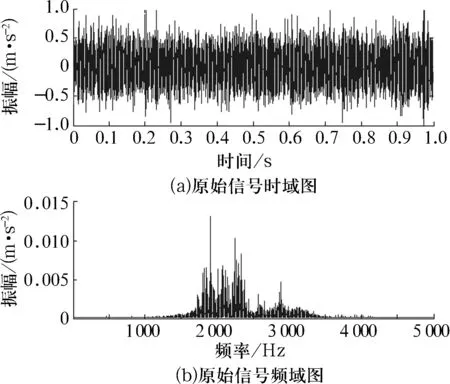
圖4 內圈故障信號波形及頻譜圖

對內圈故障信號進行EEMD處理，分解得到15個IMF分量，其中前3個IMF分量的時域波形如圖5所示。取偏移周期數M=5[4]，根據(1)式計算各IMF分量的相關峭度值，分布曲線如圖6所示。選取相關峭度值最大的第2個IMF分量及次大的第1個IMF分量進行信號重構，結果如圖7a所示，與圖4a相比，沖擊成分比較突出，但仍可以看到大量噪聲，說明EEMD的去噪能力有限。對重構信號進行基于相關峭度準則的改進形態濾波，結果如圖7b所示，從該時域圖中可以看到明顯的沖擊成分，說明該方法能夠有效地抑制噪聲。

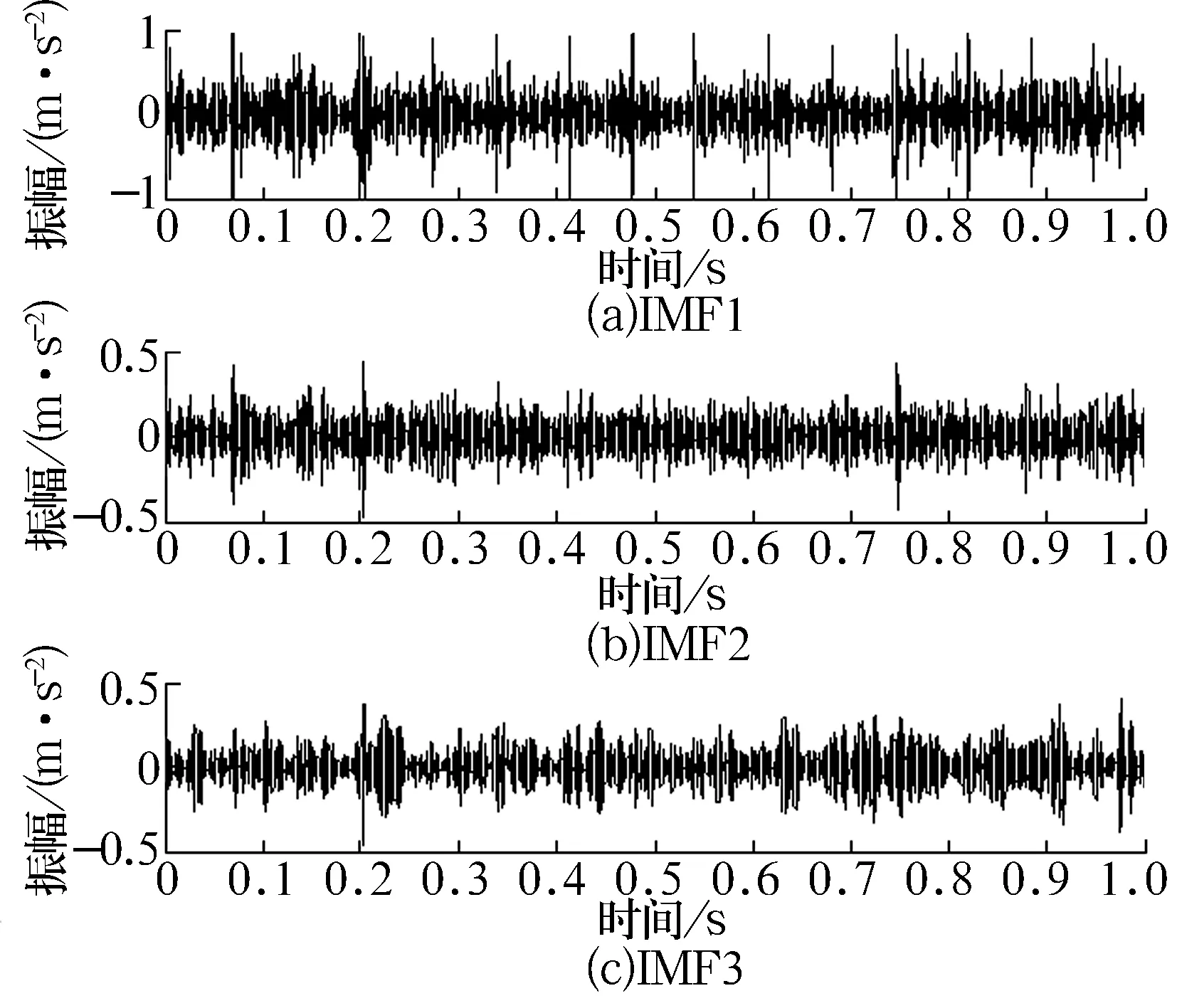
圖5 內圈故障前3個IMF分量

分別對原始信號、重構信號及重構后濾波信號進行處理，得到的Hilbert包絡譜如圖8所示。從圖中可以看出：原始信號中只能看到內圈故障特征頻率(79.09 Hz，接近內圈理論故障特征頻率79.6 Hz)，且周圍存在較強的干擾；重構信號中的1倍頻比較突出，2倍頻譜線勉強可以找到，整體解調效果不佳；重構后濾波信號中可清晰地看到轉頻 (14.69 Hz，接近轉頻理論值14.7 Hz)，故障特征頻率79.09 Hz、2倍頻158.2 Hz和3倍頻238.8 Hz，譜線都很突出，而且包絡譜中以各階倍頻為中心在其兩旁有間隔等于轉頻的調制譜線，綜合分析可診斷為內圈故障，也驗證了該方法的正確性和有效性。

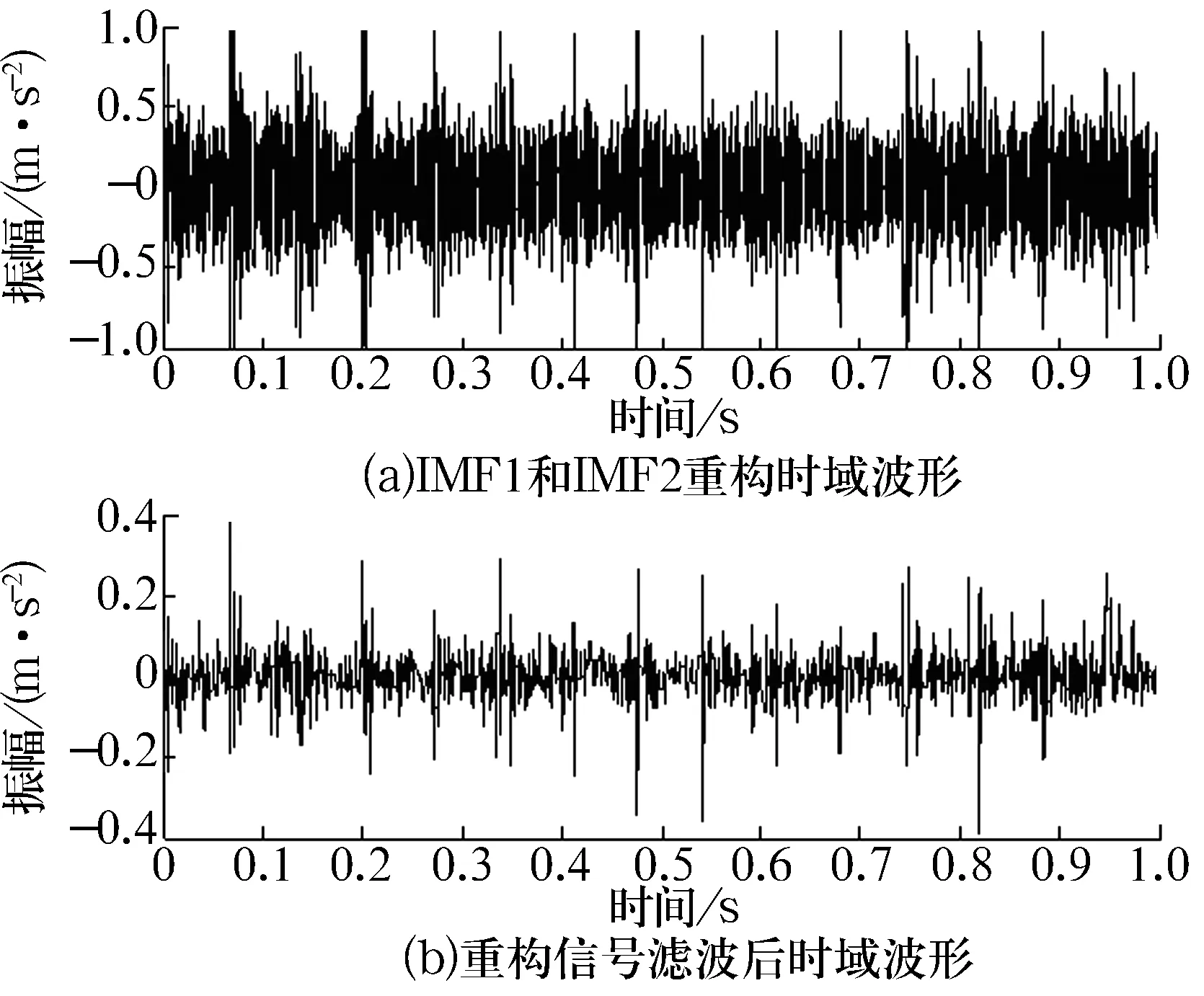
圖7 重構信號濾波前、后時域圖

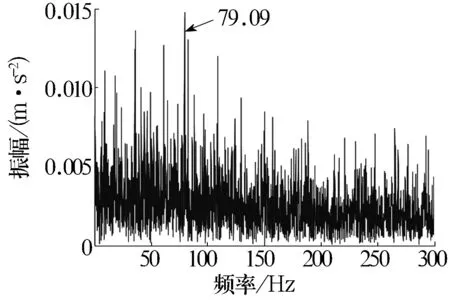
(a)原始信號

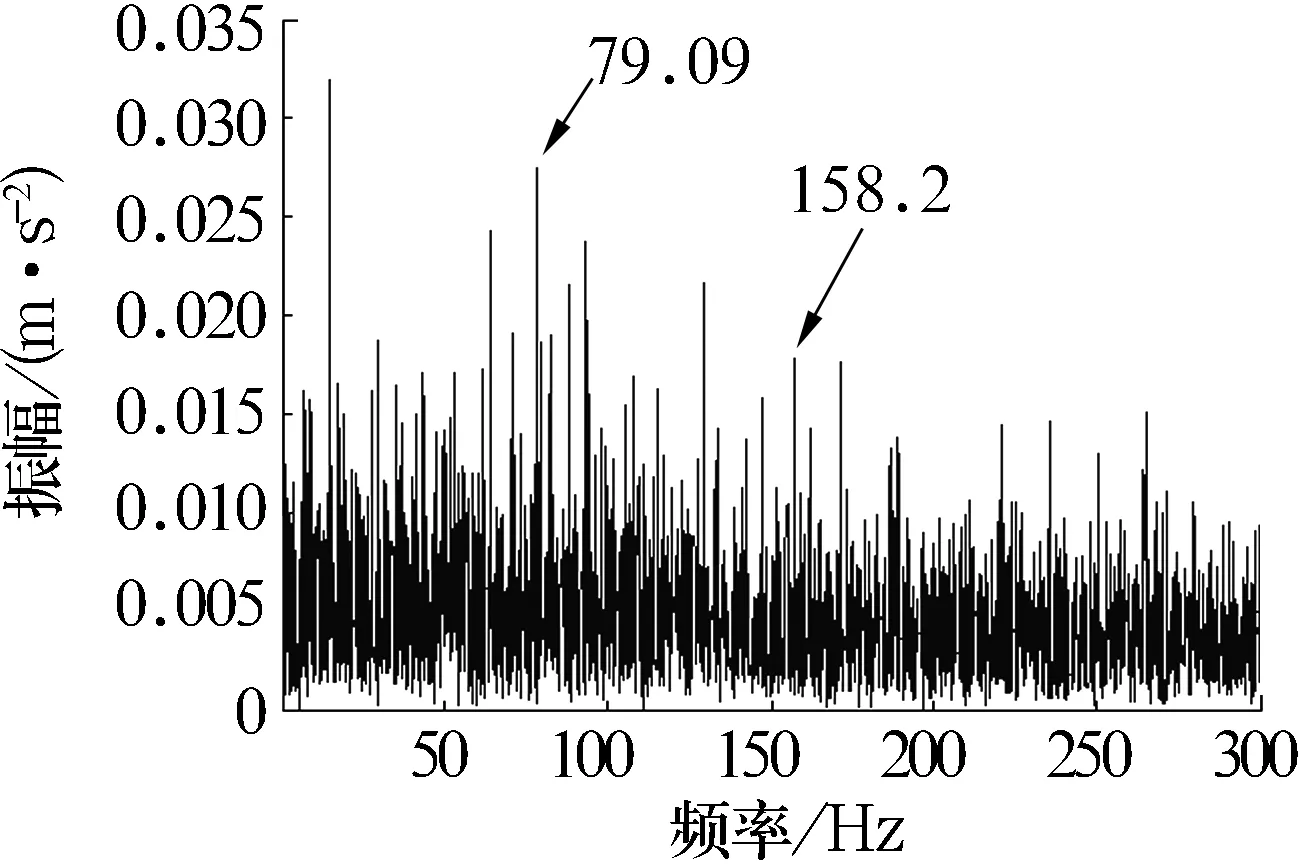
(b)重構信號

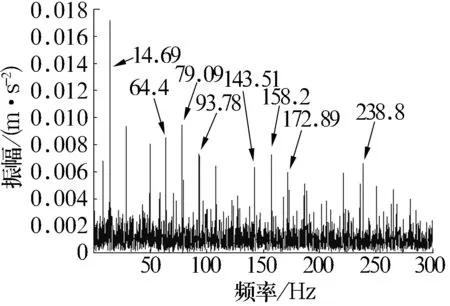
(c)重構后濾波信號

4 結束語

針對軸承故障特征信息易被噪聲污染的特點，提出了一種基于EEMD和形態濾波相結合的軸承故障診斷方法。將相關峭度應用于IMF分量的選取，能更加有效地提取微弱故障信息；基于相關峭度值最大原則的形態學濾波器可自適應地確定結構元素長度，克服了傳統形態濾波器結構元素長度選取的任意性和經驗性，能最大限度地保留故障沖擊成，實現最優濾波；EEMD與形態濾波相結合，充分發揮各自優勢，使得該方法濾波能力強、故障特征提取精度高，且易于實現，更適用于軸承的精確故障診斷。