模型參考自適應PID控制在磁軸承中的應用

張建生，馬嘯宇，王一夫，章竹耀，吳璇

（1.南通大學 電氣工程學院，江蘇 南通 226019；2.常州工學院 電氣與光電工程學院，江蘇 常州 213002）

主動磁浮軸承系統（Active Magnetic Bearing System）利用電磁力使軸承轉子穩定懸浮［1］，轉子轉速高、無機械磨損、無需潤滑介質，系統可維護性高，維護成本較低。懸浮技術的應用條件相當苛刻，目前應用于軍工、航天等重要領域［2］。主動磁懸浮軸承系統的數學模型表明其非線性且開環不穩定，需增加其他環節來實現轉子穩定懸?。?］。

常規PID控制因算法簡單、參數整定困難及魯棒性差等問題，難以達到對主動磁軸承轉子的穩定懸浮控制要求。文獻［3］采用改進的BP神經網絡PID控制算法，找到某一最優控制規律下的PID參數，該算法有較強的非線性映射能力、自學習及自適應能力，但收斂速度慢、預測與訓練能力有矛盾、從問題中選取典型樣本實例組成訓練集有很大難度。文獻［4］在分析模擬PID控制器與數字PID控制器優缺點基礎上，提出數模混合式PID控制器，使系統的響應速度及參數調節能力得到一定改善，但仍屬于簡單PID控制范疇，其固有缺點難以消除。文獻［5］研究了模糊自適應PID控制，改善了系統的動、穩態性能，抗干擾能力及魯棒性較強，但算法的模糊規則及隸屬函數的建立完全憑經驗且規則較難建立。為此，將模型參考自適應PID控制器應用到主動磁懸浮系統中，通過仿真分析驗證其控制效果。

1 主動磁懸浮控制系統建模

單自由度主動磁懸浮控制系統原理如圖1所示。系統中轉子采用上、下電磁鐵差動激勵方式。圖中：Ur為參考輸入；Ul為信號調理電路處理位移信號值l后得到的電壓信號；Uε為Ur與Ul的差值信號；Uc為控制器輸出控制信號；I0為偏置電流；f1，f2分別為上、下電磁鐵對轉子的吸力；i為上、下電磁鐵吸力變化導致的電流改變值；l為轉子受到擾動導致偏離平衡位置的距離。

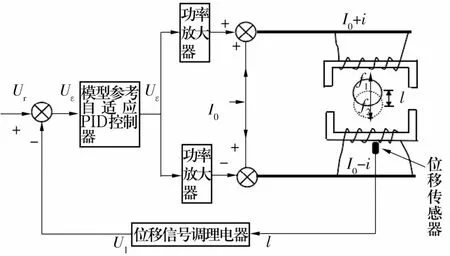
圖1 單自由度主動磁懸浮控制系統原理圖Fig.1 Principle diagram of active magnetic bearing control system with single degree of freedom

采用文獻［3-7］中的差動激勵方式建模，得到系統的開環傳遞函數為［8］

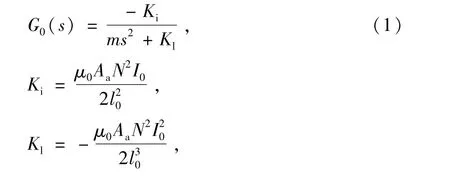
式中：Ki為電流剛度系數；Kl為位移剛度系數；μ0為真空磁導率；Aa為氣隙面積；N為線圈匝數；I0為偏置電流；l0為平衡點位置。令（1）式分母為零，發現有一正根存在，根據Routh判據判定系統為開環不穩定系統［2，9］。

2 模型參考自適應PID控制器

2.1 控制系統組成

將模型參考自適應PID控制算法應用到主動磁懸浮軸承系統中，控制系統結構框圖如圖2所示。

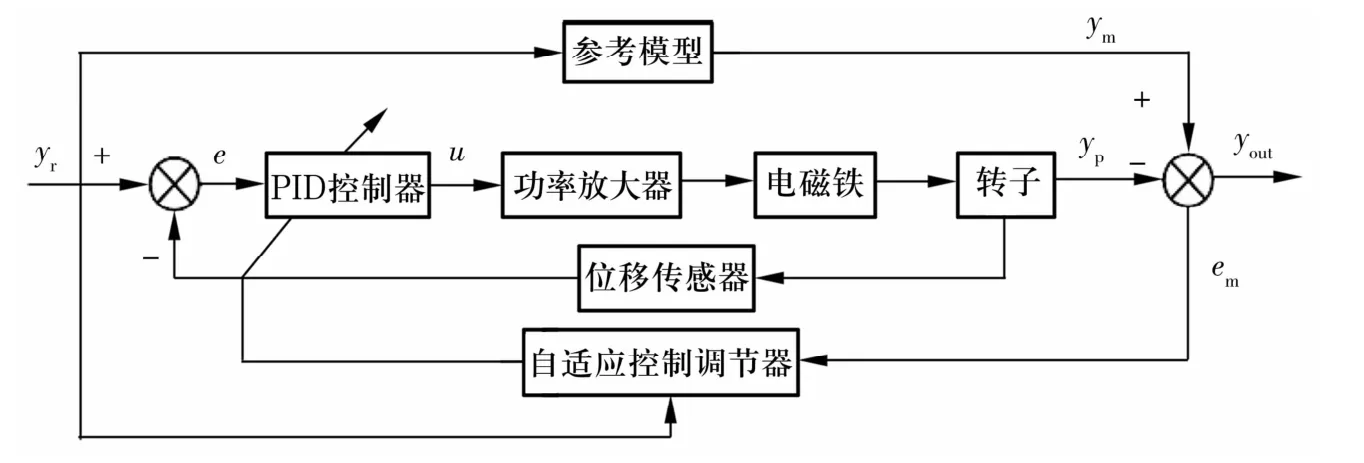
圖2 主動磁懸浮軸承模型參考自適應PID控制系統結構框圖Fig.2 Structure diagram of reference adaptive control system for active magnetic bearing model

圖2中：yr為轉子初始穩定懸浮位置；yp為轉子的實際位置；ym為轉子實現穩定懸浮的理論參考位置；e為轉子從初始穩定懸浮位置相對實際位置的偏差信號；em為自適應控制誤差信號；u為模型參考自適應PID控制器的輸出信號；yout為系統輸出響應。控制器以轉子所在位置與初始穩定懸浮位置間的位移偏差作為控制輸入信號，根據算法建立的參考模型與系統開環傳遞函數模型比較得到自適應控制誤差，再驅動自適應調節器調整PID控制器參數kp，ki，kd，以不斷減小系統誤差，得到的控制信號通過改變上、下電磁鐵線圈中的電流大小來調整轉子的位置，使轉子能夠穩定懸浮。

2.2 控制算法推導

根據單自由度主動磁軸承系統模型，以上、下電磁鐵中輸出電流i作為輸入量，以懸浮轉子受擾動發生偏移經位移傳感器檢測后獲得的輸出電壓Ul為輸出量，得到主動磁軸承系統的輸入輸出開環傳遞函數為

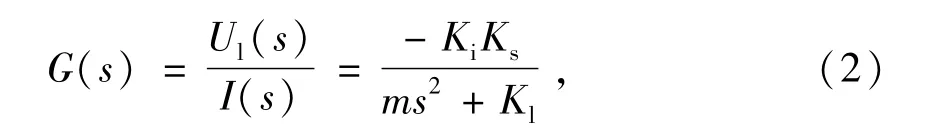
式中：Ks為位移傳感器增益。由（2）式可知，開環傳遞函數的相對階為2，故根據模型參考自適應PID控制算法設被控對象的系統狀態方程［10-11］為

式中：xp為n維狀態向量；u為控制量；yp為輸出量；Ap為n×n矩陣；bp，hp為n×1向量。

根據（2）式和（3）式建立主動磁軸承輸入輸出傳遞函數為

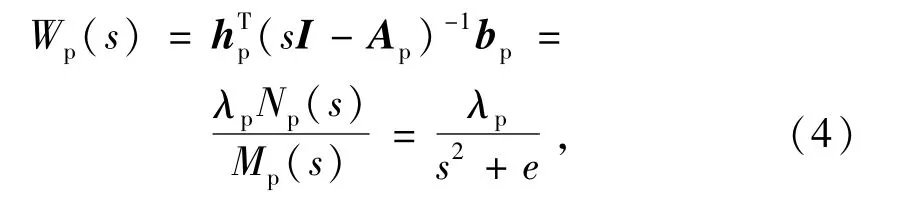
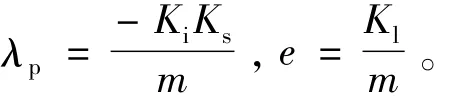
根據被控對象開環傳遞函數結構，選取磁懸浮軸承系統參考模型為

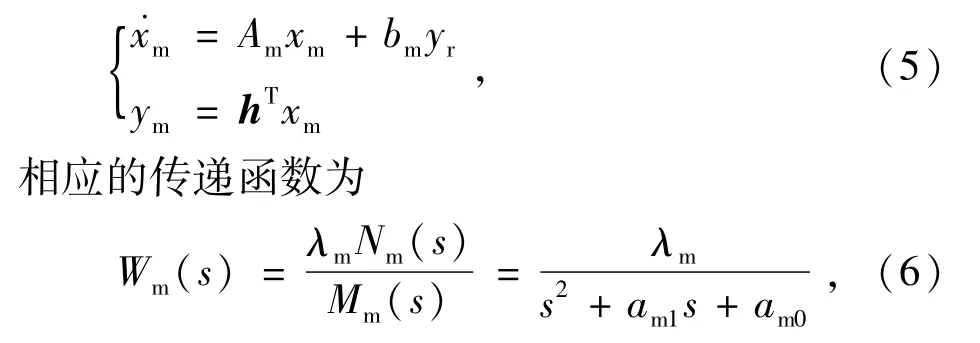
式中：Nm（s）＝1，λm＞0為參考模型增益；am1，am0為多項式一次項及常數項系數。Wm（s）的選取應為穩定最小相位系統并且與Wp（s）階數及相對階相同，還要有理想的動態性能。Mm（s）和Nm（s）分別為n階和m階首項為1的Hurwitz多項式。

從（4）式、（6）式可知，被控對象及參考模型的傳遞函數相對階均為2，故Wm（s）不具有正實性，為保證 Wm（s）嚴格正實，引入一個多項式P（s），使 P（s）Wm（s）嚴格正實，取

式中：d0為可調參數；cT＝［c1，c2，…，cn-1］，dT＝［d1，d2，…，dn-1］cT，dT為參數可調向量；S（s）為n-1階首項為1的穩定多項式；C（s），D（s）為n-2階多項式。

控制器以轉子所在位置與初始穩定懸浮位置間的位移偏差作為控制輸入信號，根據算法建立參考模型與系統開環傳遞函數模型比較得到自適應控制誤差em，驅動自適應調節器調整PID控制器參數kp，ki和kd，以不斷減小系統誤差，再通過控制器的輸出信號u改變上下電磁鐵線圈中電流大小以調整懸浮轉子懸浮位置，使轉子實現穩定懸浮。增量式PID控制算法［11］為

3 系統仿真與分析

單自由度磁軸承懸浮系統試驗平臺如圖3所示。相關參數：轉子質量m＝12 kg，功率放大器增益 Ka＝3.5 A／V，電流剛度系數 Ki＝418.25 N／A，位移傳感器增益 Ks＝5 000 V／m，位移剛度系數Kl＝-2.201 8×106N／m。單自由度主動磁懸浮軸承控制系統結構框圖如圖4所示。

圖3 單自由度磁軸承懸浮系統試驗平臺Fig.3 Experimental platform of single degree of freedom magnetic bearing

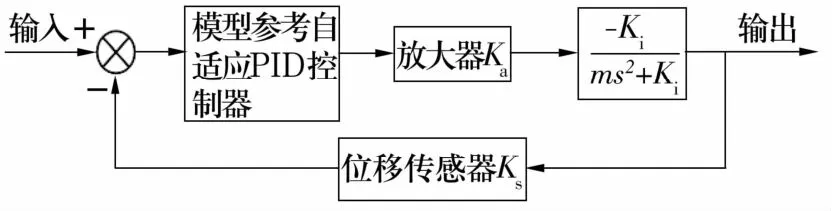
圖4 單自由度主動磁懸浮軸承控制系統結構框圖Fig.4 Control system structure of active magnetic bearing with single degree of freedom

利用MATLAB／Simulink進行系統仿真，以 C語言編寫磁懸浮軸承系統的模型參考自適應PID控制算法［10-12］。未受擾動時的系統輸出響應曲線如圖5所示，PID控制器參數的整定曲線如圖6所示。

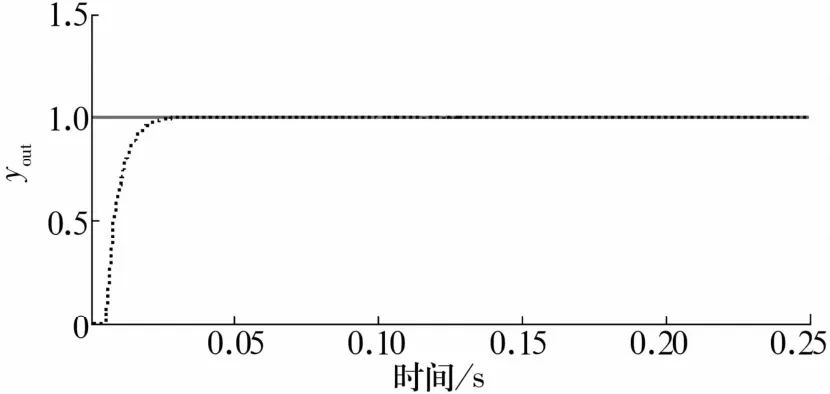
圖5 未受到擾動時系統輸出響應曲線Fig.5 Output response curve of system without disturbance

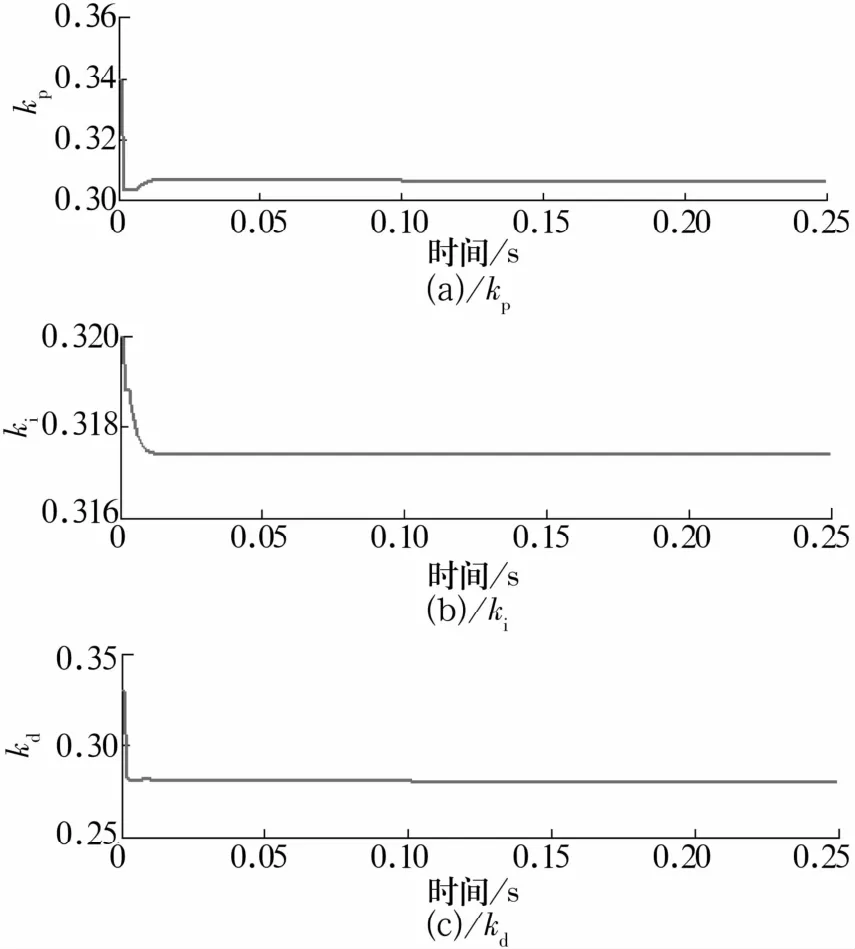
圖6 PID參數整定曲線Fig.6 Tuning curve of PID parameters

由圖5、圖6可知，在無外部擾動情況下，磁懸浮軸承轉子可實現穩定懸浮且幾乎無超調，響應速度快，調節時間ts≈0.03 s。系統的動態性能、穩態性能均較好，此時得到控制器kp，ki，kd的整定參數分別為0.31，0.318，0.28。在 t＝0.1 s時給系統一個擾動信號，系統輸出響應曲線如圖7所示。經過約0.02 s干擾信號被抑制，轉子回到穩定懸浮位置，證明系統具備抗干擾能力。

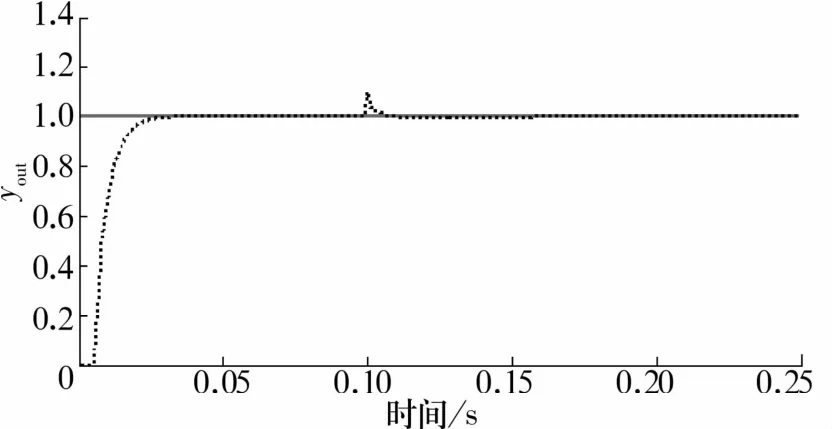
圖7 受到擾動時系統輸出響應曲線Fig.7 Output response curve of the system when the system is disturbed

常規PID控制算法與模型參考自適應PID控制算法都能達到使轉子穩定懸浮的目的。與常規PID控制算法相比，模型參考自適應PID控制算法系統輸出響應速度更快，超調量小，調節時間短，系統動、穩態性能更好（圖8）。

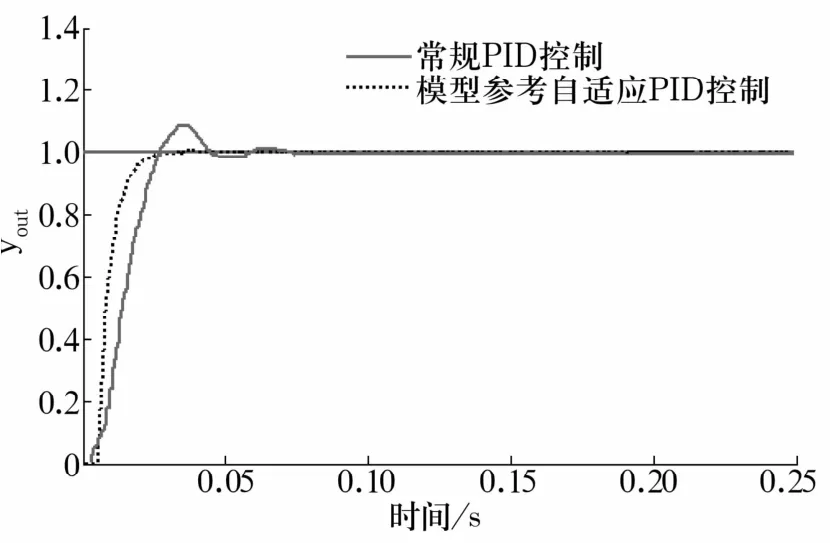
圖8 2種控制算法下系統輸出響應曲線對比Fig.8 Comparison of output response under two kinds of control algorithm

4 結束語

常規PID控制因算法簡單、參數整定困難及魯棒性差等問題，難以達到對主動磁軸承轉子的穩定懸浮控制要求，限制了其在高精度控制系統中的應用。模型參考自適應PID控制通過參考模型與被控對象的比較，在線整定控制參數，使轉子實現穩定懸浮，在有擾動情況下系統具有較強的抗干擾及恢復能力，控制效果優于常規PID控制。