基于帶權核范數最小化和混合高斯模型的去噪模型

孫少超

(公安海警學院 電子技術系，浙江 寧波 315801)

基于帶權核范數最小化和混合高斯模型的去噪模型

孫少超*

(公安海警學院 電子技術系，浙江 寧波 315801)

(*通信作者電子郵箱shaochao0631@sina.com)

非局部自相似性(NSS)先驗在圖像恢復中發揮重要作用，如何充分利用這一先驗提高圖像恢復性能仍值得深入研究，提出一種基于帶權核范數最小化和混合高斯模型的去噪模型。首先，采用混合高斯模型(GMM)對無噪聲的自然圖像非局部自相似圖像塊進行訓練，再用訓練好的混合高斯模型指導退化的圖像產生非局部自相似圖像塊組; 然后，結合帶權的核范數最小化技術實現圖像的去噪, 并對模型的保真項進行一般性擴展，給出收斂的求解算法。仿真實驗表明，所提方法與基于3D濾波的塊匹配(BM3D)算法、同時稀疏編碼學習(LSSC)算法和帶權的核范數最小化(WNNM)模型相比，峰值信噪比(PSNR)提高0.11 ～ 0.49 dB。

圖像去噪；非局部自相似性；核范數最小化；混合高斯模型

0 引言

圖像去噪作為低層視覺中的經典問題，已經被廣泛地研究，但它仍然是一個活躍的課題。在一般情況下，圖像去噪的目的是從它的噪聲觀測y=x+v中來恢復無噪聲的圖像x，其中v假設為噪聲。各種圖像去噪方法在過去的幾十年中已經被提出，包括基于濾波的方法[1]、基于混合的方法[2]、基于全變分的方法[3]、基于小波和曲波的方法[4]、基于稀疏表達的方法[5]和基于非局部自相似性(Nonlocal Self-Similarity, NSS)的方法[6]等。

自然圖像往往有許多重復的局部模塊，一個局部圖像塊可以在整個圖像找到許多類似的圖像塊, 這種被稱為非局部自相似性先驗是圖像恢復中很成功的先驗。為了利用這一先驗知識，代表性的有基于稀疏表達的方案，該方案是把圖像塊看成從字典中選擇幾個元素的線性組合[7]。其中字典可以從現成的詞典選擇(例如小波和曲波)，也可以從自然圖像塊中學習得到。文獻[8]提供了字典學習的方法，并成功地擴展到各種圖像處理和計算機視覺應用。通過把圖像塊看作是多元變量向量的樣本并考慮到自然圖像是非高斯的，Yu等[9]利用高斯混合模型對圖像塊進行建模，并分別取得了先進的去噪技術和圖像復原技術的成果。非局部均值[10]和非局部正規化[11]的方法，與傳統的基于局部自相似性的方法相比，極大地提高了圖像去噪效果。

雖然非局部自相似性先驗在圖像去噪中發揮重要的作用，但是目前存在的方法僅僅利用噪聲圖像的非局部自相似性。如基于3D濾波的塊匹配(Block Matching with 3D filtering, BM3D)算法[12]收集噪聲圖像的非局部自相似塊組成的立方體，并對其進行協同濾波的方式實現圖像的去噪。Mairal等[13]提出了同時稀疏編碼學習(Learned Simultaneous Sparse Coding, LSSC)算法，通過組合稀疏編碼來恢復NSS。文獻[14]方法中認為NSS小塊組成的矩陣奇異值服從拉普拉斯分布。Dong等[5]把NSS和局部稀疏編碼集成到一個框架中，這個框架顯示出了強大的圖像復原能力。通過假設矩陣的非局部相似的小塊有一個低秩的結構，基于低秩最小化的方法[15-16]也取得了非常有競爭力的去噪效果。然而這些模型都忽視了外部干凈圖像的非局部自相似先驗，因此本文應用混合高斯模型(Gaussian Mixed Model, GMM)獲取外部干凈圖像的非局部自相似先驗，并將其應用到帶權的核范數最小化(Weighted Nuclear Norm Minimization, WNNM)圖像去噪模型中，提高模型的去噪性能。

1 帶權的核范數最小化圖像去噪算法

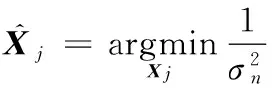
(1)

顯然，該模型的主要問題是權向量w的確定。權重向量與對應的奇異值成反比[17]，于是得到如下的權重公式：

(2)

這里σi(Xj)是圖像塊組Xj對應的第i個奇異值，c是一個常數，n是Yj中相似的分塊的數量，ε=10-16是為了避免分母為0。由于算法中σi(Xj)的奇異值不能直接獲得。

σi(Xj)可以近似估計為:

(3)

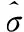
算法1。

1)

2)

k=1:L,執行

3)

4)

對y(k)每一小塊yj執行 {尋找相似分塊集合Yj奇異值分解[U,Σ,V]=SVD(Yj) 根據式(2)計算估計權向量w獲得估計：X^j=USw(Σ)VT}

5)

算法1中Sw(Σ)ii被定義為:

Sw(Σ)ii=max(Σii-wi,0)

(4)

2 基于GMM和WNNM的混合去噪模型

自然圖像通常有一些重復的局部模式， 并且對于一個局部的圖像塊在整個圖像中可以找到許多與之相似的圖像塊，這些圖像塊組成的矩陣通常是低秩的，這個被稱為非局部自相似的先驗是圖像恢復最成功的先驗之一。

帶權核范數最小化圖像去噪模型收集歐氏距離相近的圖像塊向量組成非局部自相似矩陣，這個非局部自相似矩陣的質量好壞直接影響去噪性能。當圖像受到噪聲污染，根據退化圖像的歐氏距離來組成非局部自相似矩陣是存在問題的，因為噪聲會影響非局部自相似矩陣的組成，進而影響該矩陣的低秩性，導致NSS先驗失敗。

在圖像去噪中僅利用退化圖像的非局部自相似性先驗是不夠的，可以利用外部的無噪聲自然圖像的非局部自相似性的先驗。為此本文對無噪聲的自然圖像的非局部自相似性圖像塊進行訓練產生外部NSS先驗的GMM，然后用該GMM指導退化圖像生成非局部自相似塊矩陣，最后用WNNM算法進行圖像的去噪。這種結合退化圖像本身的NSS先驗和外部干凈圖像NSS先驗得到的非局部自相似塊矩陣質量更高，有助于提升圖像的去噪效果，這點也通過后面的仿真實驗得以驗證。

可以假設自然圖像塊源于一個K維子空間的潛在結構，所以一個給定的圖像塊xi的概率可以被定義為K個高斯的加權和，如式(5)所示：

引入類標簽變量C∈{1,2,…,K}。對于每一塊xi,本文用GMM學習的概率密度函數(Probability Density Function, PDF)來判斷xi屬于哪一類Ci，式(6)表示屬于第k類的概率：

(6)

根據式(6)找出其中的最大值賦值給Ci； 然后，對于給定圖像塊xi，本文根據式(7)的馬氏距離來尋找與它相似的非局部分塊，形成非局部相似矩陣Yj，最后應用WNNM模型對含噪聲圖像進行去噪，詳細步驟見算法2。

(7)

算法2。

1)選定K,對自然無噪聲的圖像塊用GMM方法進行訓練，得到參數Θ

3)k=1:L,執行

5)對y(k)每一小塊yj根據式(6)計算Ci根據式(7)尋找相似分塊集合Yj，根據式(2)估計權向量w奇異值分解[U,Σ,V]=SVD(Yj) 獲得估計：X^j=USw(Σ)VT

3 模型的擴展及收斂性分析

上述方法解決的式(1)所示的去噪模型，該模型中的保真項，適用于高斯噪聲的特點，因此對高斯噪聲有很好的抑制效果，然而當對均勻噪聲等其他噪聲或者圖像中還有粗差的效果不好，因此需要對式(1)所示的去噪模型的優化目標進行修正為：

F(Xj)=h(Xj)+‖Xj‖w,*

(8)

其中h(·)為在Rm×n→R+利普希茨連續可導函數，利普希茨常數為L(h)，h(·)替換式(1)中的保真項更具一般性，對模型(8)求最小值可以利用下面的更新策略求解：

(9)

其中μ>L(h)。

收斂性分析：

為了證明上述擴展模型的收斂性，需要證明當μ>L(h)則數列由式(9)獲得的序列{Xk}滿足以下特性：

1)F{Xk}是單調遞減的，即

證明 因為Xk+1是式(9)的最優解，可以得到式(10):

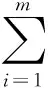
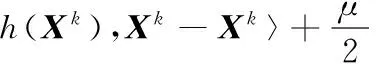
(10)

另一方面，因為h在利普希茨連續可導，所以可以得到:

h(Xk+1)≤h(Xk)+〈▽h(Xk),Xk-Xk〉+

(11)

根據式(10)和(11)可以得到:

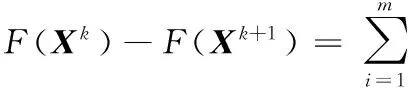
(12)

由于μ>L(h)，所以F(Xk)≥F(Xk+1)。

將式(12)對k=1,2,3，…進行累加可得到：

(13)

進而得到：

(14)

從而得到模型的斂散性。

4 仿真實驗

為了驗證上面提出算法的有效性，本文將算法應用到實際的例子中，并將本文算法跟其他經典的算法(包括BM3D[12]、LSSC[13]和WNNM[15])作比較。本實驗的計算機為普通PC，計算機的配置為CPU i7-4770k,內存為12 GB。為了使本文的仿真實驗更加逼近真實情況，文中添加的噪聲為不同噪聲類型的疊加。本文訓練GMM的樣本來自Berkeley數據集，從這些圖像中提取了2×106個圖像塊。圖像塊的尺寸和很多文獻一樣設置為7×7、8×8、9×9和10×10，分別針對方差在[0,20]、[20,40]、[40,60]和[60,100]四種情況。

下面本文將就算法性能(文中采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)作為評價指標)和算法的運行效率兩方面進行比較說明。

限于篇幅，圖1和圖2分別給出了C.man 和Monarch這兩張圖片在噪聲方差為30、50，本文算法與其他先進的算法去噪的直觀效果。

圖1 噪聲方差為30時不同算法的去噪效果比較Fig. 1 Denoising results by different methods (noise variance=30)

表1顯示了在噪聲方差為30、50、100的情況下PSNR性能的比較。從實驗結果可以看出BM3D性能平均提高了0.49 dB,相對于LSSC算法提高了0.38 dB,相對于WNNM算法平均提高了0.11 dB。本文的算法相對于BM3D算法和LSSC算法有顯著的提高，相對于WNNM算法也有明顯的提升。這些提升也驗證了本文用混合高斯模型學習外部無噪聲的圖像的非局部自相似性這一先驗知識，并在這一先驗知識的指導下采用馬氏距離來形成非局部自相似圖像塊矩陣，代替其他算法采用歐氏距離形成非局部自相似圖像塊矩陣更加合理。

表1 不同算法的PSNR比較 dBTab. 1 Peak signal-to-noise ratio after denoising results by different methods dB

此外，需要注意的是，本文算法在大噪聲的情況下相對于其他算法優勢更明顯，在噪聲方差為100時，本文算法相對于BM3D算法性能平均提高了0.65 dB,相對于LSSC算法提高了0.59 dB,相對于WNNM算法平均提高了0.156 dB。本文方法隨著噪聲方差的增加去噪優勢更加明顯。

圖2 噪聲水平為50時不同算法的去噪效果比較Fig. 2 Denoising results by different methods (noise variance=50)

表2顯示了本文算法與其他先進算法處理256×256圖像的時間運行時間的比較，算法的實驗結果是在不同的噪聲方差下，對不同圖像運行100次的平均時間。從表4可以看出，雖然本文算法運行時間與WNNM相當，高于BM3D算法，但相對于WNNM來說犧牲很少的運行效率卻獲得了更好的去噪效果。

表2 不同算法運行時間的比較 sTab. 2 Running time of different methods s

5 結語

本文首先用無噪聲的自然圖像塊訓練混合高斯模型;然后再用訓練好的混合高斯模型指導采集非局部自相似塊，用馬氏距離代替歐氏距離來衡量圖像塊之間的相似性，并為了使模型更具一般性，提出了擴展模型; 最后，為了驗證本文算法的有效性，與一些先進的算法進行仿真實驗，仿真結果表明，所提算法在很多情況下具有優勢。

References)

[1] TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]// Proceedings of the 6th International Conference on Computer Vision. Piscataway, NJ: IEEE, 1998: 839-846.

[2] PERONA P, MALIK J. Scale-space and edge detection using anisotropic diffusion [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(7):629-639.

[3] OSHER S, BURGER M, GOLDFARB D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling & Simulation, 2005,4(2):460-489.

[4] STARCK J L, CANDES E J, DONOHO D L. The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing, 2002,11(6):670-684.

[5] DONG W, ZHANG L, SHI G, et al. Nonlocally centralized sparse representation for image restoration [J]. IEEE Transactions on Image Processing,2013,22(4):1620-1630.

[6] JI H, LIU C, SHEN Z, et al. Robust video denoising using low rank matrix completion[J]. Computer Vision & Pattern Recognition, 2010, 23(3):1791-1798.

[7] ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries [J].IEEE Transactions on Image Processing, 2006,15(12):3736-3745.

[8] AHARON M, ELAD M, BRUCKSTEIN A. TheK-SVD: an algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006,54(11):4311-4322.

[9] YU G, SAPIRO G, MALLAT S. Solving inverse problems with piecewise linear estimators: from Gaussian mixture models to structured sparsity [J]. IEEE Transactions on Image Processing, 2012, 21(5):2481-2499.

[10] BUADES A, COLL B, MOREL J M. A nonlocal algorithm for image denoising[C]// Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2005: 60-65.

[11] PEYRE G, BOUGLEUX S, COHEN L D. Nonlocal regularization of inverse problems [J]. Inverse Problems and Imaging, 2011, 5(2):511-530.

[12] DABOV K, FOI A, KATKOVNIK V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J].IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095.

[13] MAIRAL J, BACH F, PONCE J, et al. Non-local sparse models for image restoration[J]. Proceedings of the 2009 IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2009: 2272-2279.

[14] WANG S, ZHANG L, LIANG Y. Nonlocal spectral prior model for low-level vision[C]// Proceedings of the 11th Asian Conference on Computer Vision. Berlin: Springer-Verlag, 2013: 231-244.

[15] GU S, ZHANG L, ZUO W, et al. Weighted nuclear norm minimization with application to image denoising[C]// Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2014: 2862-2869.

[16] JI H, LIU C, SHEN Z, et al. Robust video denoising using low rank matrix completion[J]. Computer Vision & Pattern Recognition, 2010, 23(3):1791-1798.

[17] XU J, ZHANG L, ZUO W, et al. Patch group based nonlocal self-similarity prior learning for image denoising[C]// Proceedings of the 2015 IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2015:244-252.

This work was partially supported by the Technology Research Project of Ministry of Public Security of China (2015JSYJC029), the Public Security Marine Police Academy Research Center, Research Team Research Project.

SUN Shaochao, born in 1984, Ph.D., lecturer. His research interests include machine learning, computer vision.

Image denoising via weighted nuclear norm minimization and Gaussian mixed model

SUN Shaochao*

(DepartmentofElectronicTechnology,ChinaMaritimePoliceAcademy,NingboZhejiang315801,China)

Nonlocal Self-Similarity (NSS) prioritization plays an important role in image restoration, but it is worthy of further research that how to make full use of this prior to improve the performance of image restoration. An image denoising via weighted nuclear norm minimization and Gaussian Mixed Model (GMM) was proposed. Firstly, the clean NSS image blocks of the natural image were trained by GMM, and then the trained GMM was used to guide the degraded image to produce NSS image blocks. Then, the weighted nuclear norm minimization was used to realize image denoising, an extended model was proposed by modifying the fidelity item, and the corresponding convergent algorithm was given. The simulation results show, compared with some advanced algorithms such as Block Matching with 3D filtering (BM3D), Learned Simultaneous Sparse Coding (LSSC) and Weighted Nuclear Norm Minimization (WNNM), the proposed method improves the Peak Signal-to-Noise Ratio (PSNR) by 0.11 to 0.49 dB.

image denoising; Nonlocal Self-Similarity (NSS); Nuclear Norm Minimization (NNM); Gaussian Mixed Model (GMM)

2016-10-12;

2016-11-25。

公安部技術研究計劃項目(2015JSYJC029);公安海警學院研究中心、科研團隊研究計劃項目。

孫少超(1984—)，男，山東榮成人，講師，博士，CCF會員，主要研究方向：機器學習、計算機視覺。

1001-9081(2017)05-1471-04

10.11772/j.issn.1001-9081.2017.05.1471

TP391.41

A