超靜定結構支架的受力計算

蘇瑞杰，閃修洋，李鑫

(華電鄭州機械設計研究院有限公司，鄭州 450046)

超靜定結構支架的受力計算

蘇瑞杰，閃修洋，李鑫

(華電鄭州機械設計研究院有限公司，鄭州 450046)

以超靜定結構支架為研究對象，建立力學模型，以靜力學平衡方程為基礎，在分析支架受力及變形情況的前提下，利用變形協(xié)調條件和力與位移間的物理關系建立變形補充方程，求解微分方程組后得到支架的受力情況。該計算方法與仿真分析所得結果基本吻合，偏差在允許范圍內。將該計算方法與傳統(tǒng)估算方法進行對比，該方法適用范圍更廣、結果更準確。

超靜定結構；支架；受力分析；計算

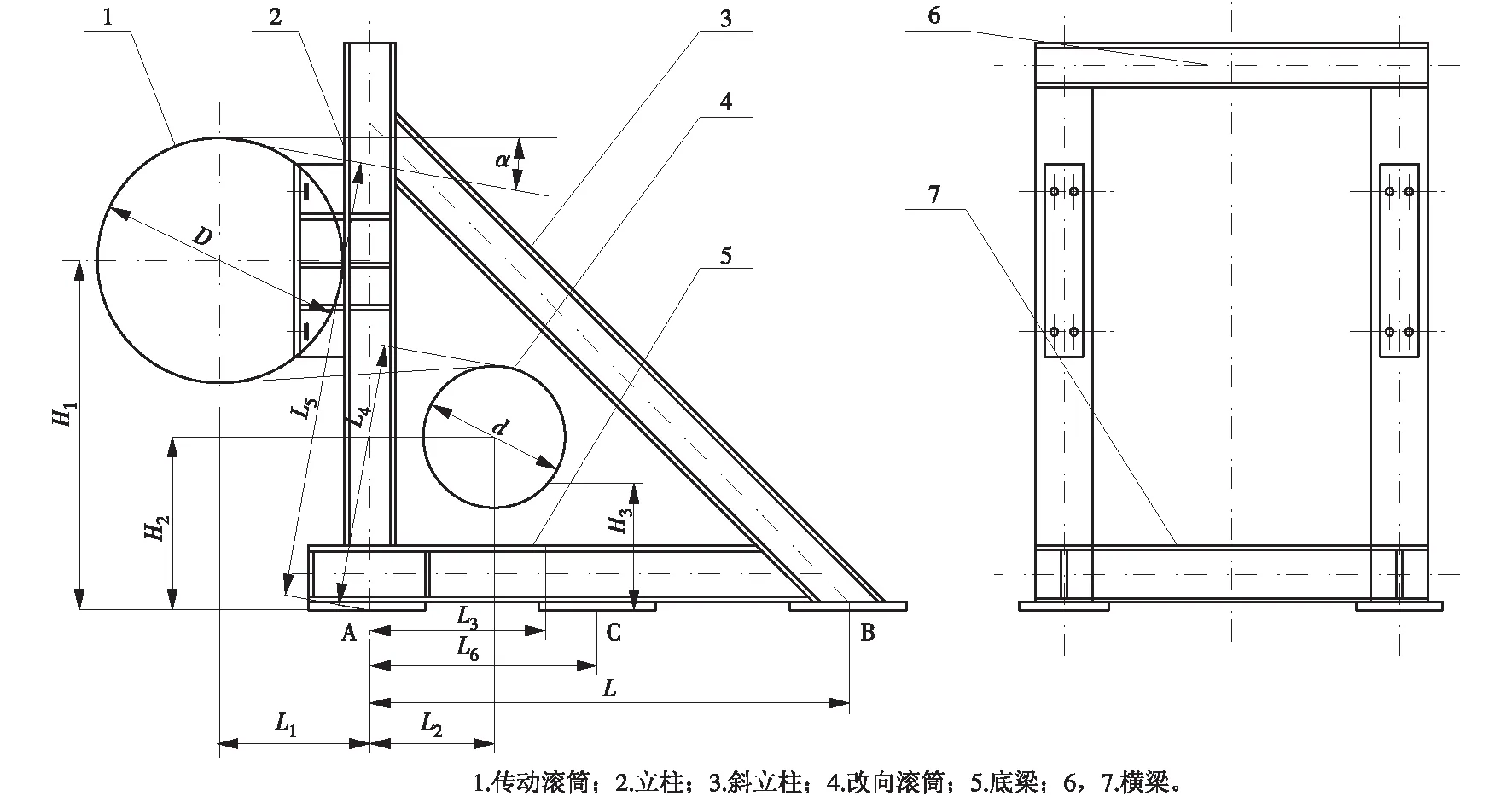
圖1 三角形滾筒支架示意

0 引言

作為支撐滾筒并承受其動靜載荷的三角形支架，結構簡單且便于安裝和維護。在工程設計過程中，需要對支架進行受力分析和計算，以確保結構安全可靠。以帶式輸送機系統(tǒng)設計為例，滾筒支架用于安裝傳動滾筒和改向滾筒并承受皮帶的張力，底座與埋鐵焊接或錨固。常見的支架底部為4點支撐，在已知皮帶拉力及設備自重和尺寸的前提下，列出力和力矩平衡方程即可得出支架的受力情況，這種計算方法忽略了結構件的變形，視其為剛體，屬于靜力學的范疇[1]。

在實際工程中，當遇到載荷較大的情形時，通常采取增加底部支撐數量的措施，以減小集中力和剪力對支架強度的影響。采用力和力矩平衡的方法對上述情況的支架進行受力計算時，未知力的數目大于有效平衡方程的數目，即成為超靜定結構。對于超靜定結構，靜力學方法已經不能滿足求解的需求。

本文以具有超靜定結構的支架為分析對象，以帶式輸送機滾筒支架為例建立力學模型，給出求解方法并與傳統(tǒng)估算方法進行對比。

1 力學模型

典型三角形滾筒支架由立柱2，斜立柱3，底梁5及橫梁6，7組成，如圖1所示，其中A，B，C 3點為錨固支座。外部作用力通過立柱和斜立柱傳遞到底梁上。槽型鋼板2，3，5，6，7通過焊接相連，可以認為其之間為剛性連接[2]；底梁上的支撐點A，B，C在設備重力及皮帶拉力的作用下，既受水平方向的力又受豎直方向上的力，可將其等價為鉸支座連接[3]，從而可使該支架等價為圖2所示的力學模型。

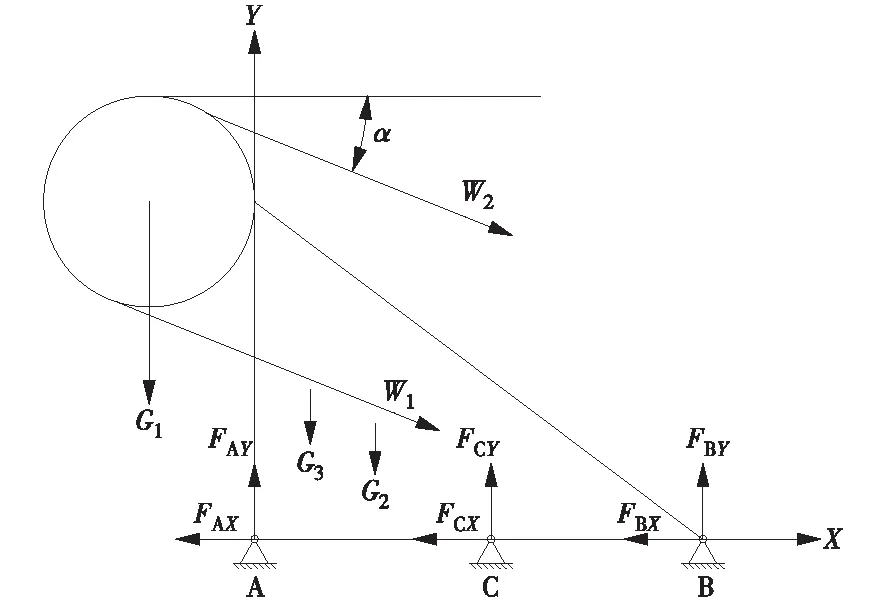
圖2 三角形滾筒支架力學模型

圖2中：G1，G2，G3分別為傳動滾筒、改向滾筒及滾筒支座的重力；W1，W2為輸送帶的拉力；未知力FAX，FAY，FBX，FBY，FCX，FCY分別為預埋件對滾筒支架A，B，C 3點的支反力，其中FAX，FBX，FCX為水平方向力，FAY，FBY，FCY為豎直方向力。

2 計算原理和方法

FAX，FBX共線且方向一致，都是由輸送帶拉力W1，W2的水平分力在軸A，B上的正應力引起的。根據受力平衡可得，水平方向上的合力為0，則

(1)

對于FAY，FBY，FCY，由系統(tǒng)平衡原理可知，其內部任一點的合力偶和合力的代數和均為0，列靜力學平衡方程

(2)

(3)

方程(2)，(3)中，未知力的數目大于方程的數目，屬于超靜定問題。在超靜定系統(tǒng)中，凡是多于維持平衡所必需的約束稱為多余約束，從上式可以看出，此系統(tǒng)中有一個多余約束。選取C處的約束為多余約束，則相應的多余支反力為FCY。

為了揭示多余支反力FCY的作用，可假想將支座C解除，而以支反力FCY代替，這樣就得到了原超靜定支座的相當系統(tǒng)。忽略剪力引起的截面翹曲，相當于系統(tǒng)在外載荷與多余支反力FCY的作用下發(fā)生彎曲變形，為使其變形與原超靜定支座相同，多余約束處C點的位移(又稱撓度)必須符合原超靜定支座在該處的約束條件，即滿足變形協(xié)調條件

(4)

式中：yC為C點的撓度，一般情況下，在力的作用下不同截面的撓度不同，所以yC=y(x=C)。

以系統(tǒng)中A點為原點，AB方向為X軸，該斷面內垂直于AB的方向為Y軸建立坐標系，則AB軸上x處的彎矩為

(5)

在變形較小且軸的內應力不超過比例極限的情況下，根據撓曲軸近似微分方程理論可知，當軸在彎矩M(x)0的作用下發(fā)生彎曲變形時，軸上x點處的撓度與彎矩的數學關系為[4]

(6)

式中：EI為剛度系數。

式(6)為線性微分方程，并且軸AB所受到的彎矩M(x)0與載荷成線性齊次關系，所以，當軸AB上有多個載荷同時作用時，撓曲軸近似微分方程的解必等于每個載荷單獨作用時撓曲軸近似微分方程解的線性組合，即所求得撓度也與載荷成線性齊次關系[5]。因此，圖2所示模型的撓曲軸近似微分方程為

(7)

(8)

式中：C1，C2為積分常數。

由于A，B處有約束，所以外載荷在A，B兩處的撓度為0，即位移邊界條件為

(9)

(10)

聯(lián)立方程(2)，(3)，(4)，(5)，(8)，(9)，(10)即可求出FAY，FBY，FCY。

3 計算實例

以圖1所示的三角形支架為例，進行受力計算，具體參數見表1。

通過上節(jié)所述計算方法求得：FAY=87.20 kN，FBY=119.40 kN，FCY=23.54 kN。其中：FBY，FCY為下壓力；FAY為上拔力。

4 軟件仿真分析

以實例計算所給的參數為依據進行三維建模，利用Ansys軟件進行有限元分析。為了便于建模，把傳動滾筒和改向滾筒上的力等效為相同重力的梁，設定A，B，C，A1，B1，C16點約束形式為鉸接，如圖3所示，這6點的集中力計算結果見表2。

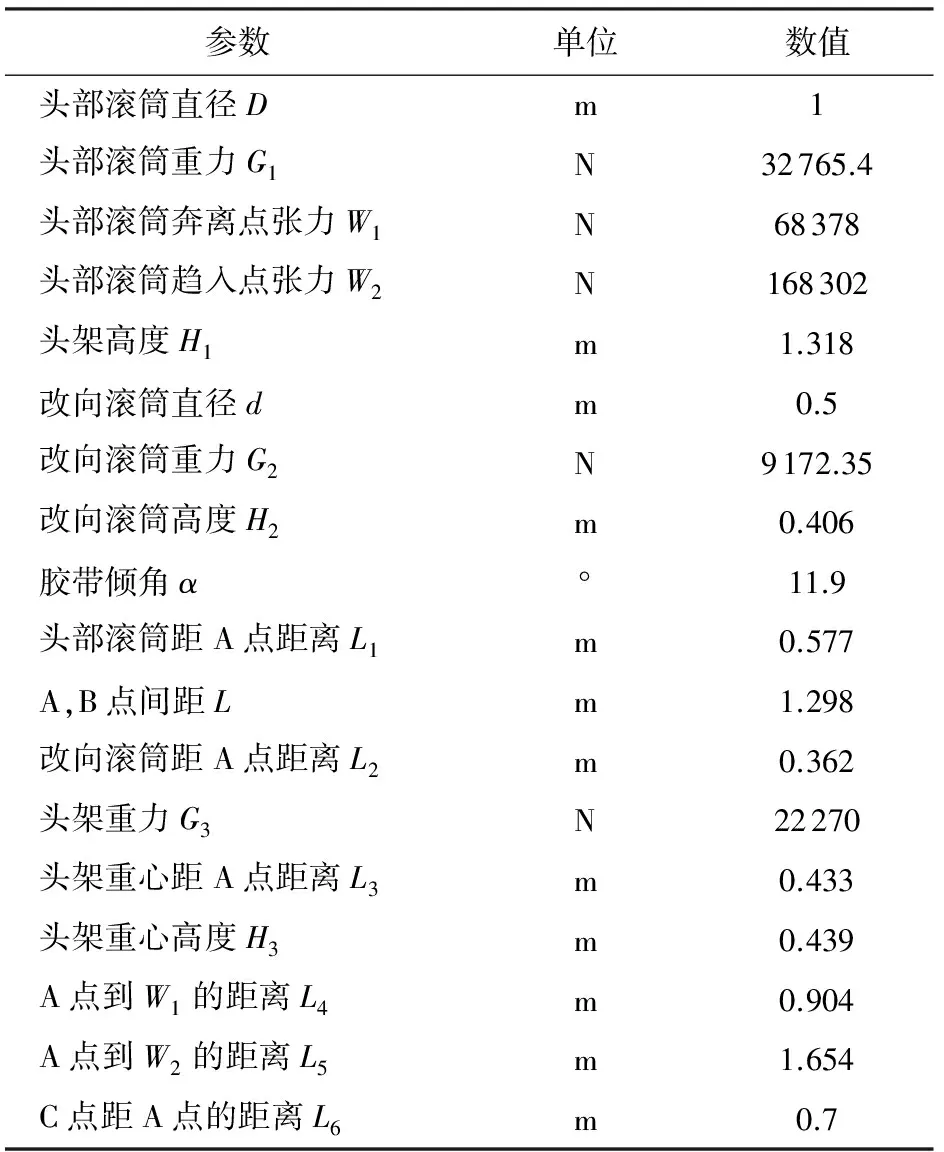
表1 支架參數

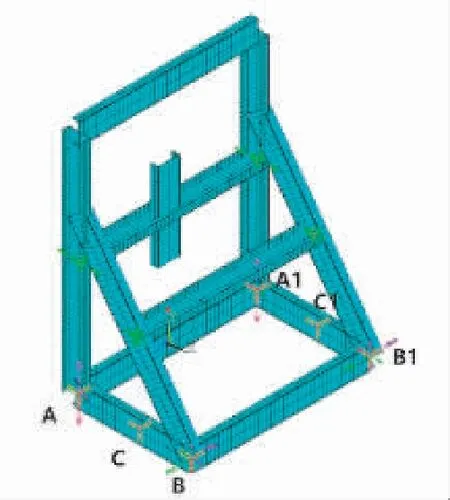
圖3 三維建模

把計算值等效到圖2所示的力學模型截面上可得：FAY=(66.358+53.620)/2=60.00 kN(上拔力)，FBY=(127.820+110.360)/2=119.09 kN(下壓力)，FCY=(19.998+15.725)/2=17.86 kN(下壓力)。

與實例計算結果對比，FBY大小一致，FAY，FCY偏小，原因如下。

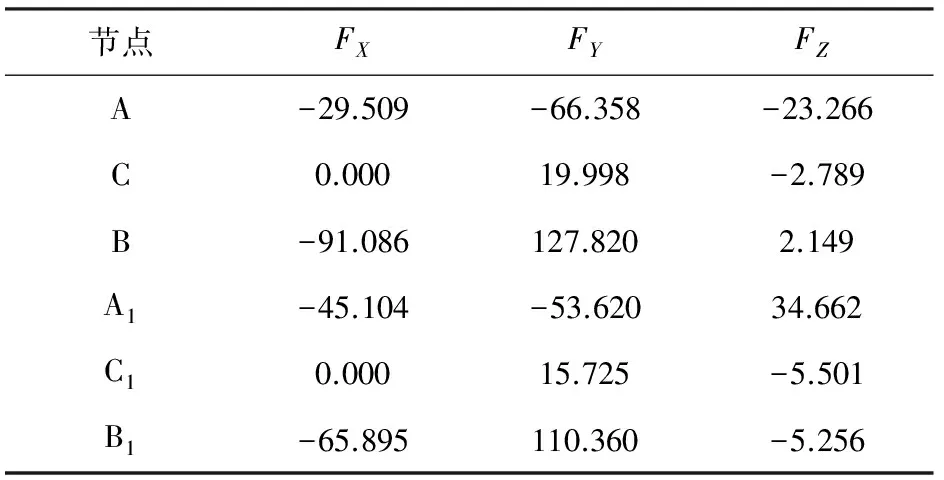
表2 集中力計算結果 N

(1)本文所述的力學建模是把支架等效為一個平面內的桿件結構，忽略了Z方向上的應力和應變對系統(tǒng)受力的影響。

(2)在Z方向，滾筒對橫梁的彎矩作用會引起梁兩端截面的翹曲，對底座有一定的反作用力，該力會抵消部分A，C上的上拔力，故而FAY，FCY偏小。

綜合對比結果分析，該計算方法與仿真分析所得的值基本吻合，偏差在允許范圍內。

5 該計算方法的優(yōu)點

在以往的工程設計計算中，遇到類似超靜定問題時，支架所受的水平分力FAX，FBX，FCX的計算方法與公式(3)相同，豎直分力FAY，FBY，FCY的計算法為：假設只有A，B兩個支撐點，通過靜力學理論，列出力和力矩平衡方程求出FAY，FBY，然后利用幾何學方法估算出C支撐點的豎直力，方法如圖4所示。

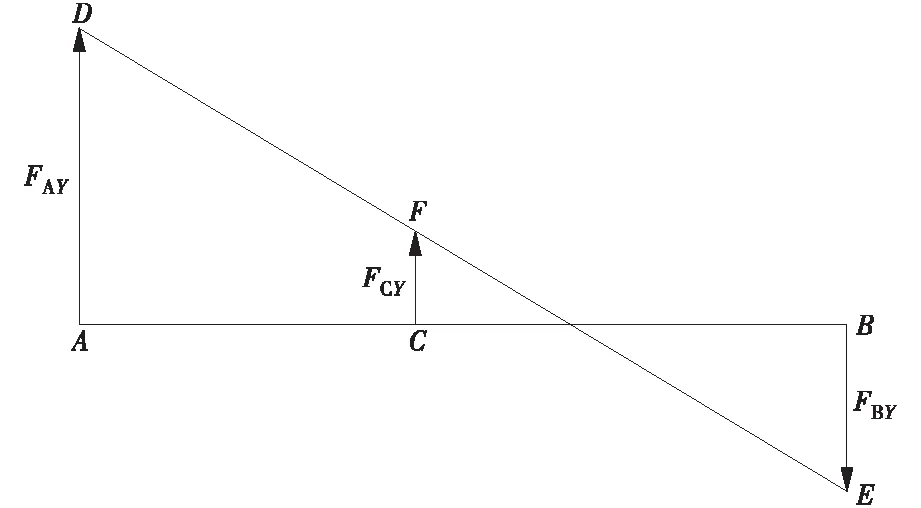
圖4 幾何法示意

圖4中，AD，BE線段的長度表示FAY，FBY的值，連接D，E兩點，以C點為起點作垂直于軸AB的垂線，交DE于點F，線段CF的值即為FCY的大小，C到F的指向即為FCY的方向。

和上述計算方法相比，本文所述計算方法有以下優(yōu)點。

(1)把支架當作彈性體，考慮其變形和撓度，力學建模和力值分析方法更加貼近實際，所求得的結果更為精確，在滿足受力要求的前提下節(jié)約了土建成本。

(2)以往計算方法是通過幾何學原理求得FCY的方向，缺乏理論依據，不利于土建專業(yè)對基礎埋件的工藝設計(受拉、受壓對土建專業(yè)工藝設計的要求是不同的)。

(3)當所求出的FAY，FBY大小相等方向相反，且C點處于AB中點時，傳統(tǒng)方法求得的FCY為 0，顯然與實際不符。相比之下，超靜定算法求得的結果更具有說服性。

(4)當支架的支撐點數量遠大于3且支架的尺寸較大時，以往計算方法所得的FAY，FBY的值(即底梁兩端支撐點的力)跟實際值相差很大，甚至出現失真，在應用范圍上具有局限性，而超靜定計算法則是普遍適用的。

[1]哈爾濱工業(yè)大學理論力學教研室.理論力學[M].北京：高等教育出版社，2009.

[2]賀克讓.大傾角帶式輸送機三角形支架設計[J].起重運輸機械，1993(2)：19-23.

[3]鄭文緯，吳克堅，鄭星河.機械原理[M].7版.北京：高等教育出版社，1997.

[4]單輝祖.材料力學教程[M].2版.北京：國防工業(yè)出版社，1997：218-220.

[5]同濟大學數學系.高等數學[M].北京：高等教育出版社，2007.

(本文責編：劉芳)

2016-07-07；

2017-06-29

TB 12

A

1674-1951(2017)07-0001-03

蘇瑞杰(1981—)，男，河南延津人，工程師，從事散料行業(yè)散料輸送及處理方面的工作(E-mail:surj@chec.com.cn)。

閃修洋(1989—)，男，河南南陽人，工程師，從事散料行業(yè)散料輸送及處理方面的工作(E-mail:shan-xy@chec.com.cn)。