基于MATLAB和LINGO的直齒錐齒輪傳動優化設計

王沁軍，吳志光

（山西機電職業技術學院機械工程系，山西長治046011）

基于MATLAB和LINGO的直齒錐齒輪傳動優化設計

王沁軍，吳志光

（山西機電職業技術學院機械工程系，山西長治046011）

以大端端面模數met，小錐齒輪齒數z1，錐齒輪寬度b作為設計變量，以錐齒輪總體積最小為優化目標，以齒輪的強度等要求作為約束條件構建出直齒錐齒輪傳動優化數學模型。通過實例給出常規設計方案，借助Matlab軟件進行連續變量優化求解，利用Lingo軟件進行離散變量優化求解，對求解結果進行綜合比較，得出優化設計方案。與常規設計相比，錐齒輪總體積下降約32%，優化效果明顯，能為設計選型提供參考。

直齒錐齒輪傳動；優化設計；連續變量；離散變量

錐齒輪傳動應用廣泛，強度條件主要為齒面接觸強度和齒根彎曲疲勞強度，對于強度校驗，按GB /T10062-2003錐齒輪承載能力計算方法進行，其傳動常規設計可以按文獻[1]和[2]進行。對于其優化設計，文獻[3]和[4]采用遺傳算法，分別對弧齒錐齒輪傳動和可控螺旋角錐齒輪傳動進行優化，文獻[5]考慮設計變量的離散性，利用枚舉法，對直齒錐齒輪傳動進行優化，文獻[6]采用混合離散復合形法，對弧齒錐齒輪傳動進行優化。對于優化設計，主要集中在利用優化求解算法，針對實際問題構建優化數學模型并進行求解。

本文以直齒錐齒輪傳動為研究對象，選取大端端面模數met，小錐齒輪齒數z1，錐齒輪齒寬b為設計變量，以兩錐齒輪體積之和最小為優化目標，確定了邊界和強度約束條件，構建出優化數學模型，利用Matlab進行連續變量優化求解，然后利用Lingo進行離散變量優化求解，綜合分析得出優化方案，優化求解結果比初始設計在總體積上得以減小32%，可為設計選型提供必要參考。

1 優化數學模型的建立

1.1 設計變量

通常設計時載荷情況，小錐齒輪傳遞的轉矩T1，齒數比u，小錐齒輪轉速n1等均可確定，此時基本設計參數為met，z1，z2，b（或ΦR），∑，δ1，δ2等[1]。其中z2為大錐齒輪齒數，ΦR為齒寬系數，∑為軸線間交角，δ1、δ2分別為小、大齒輪分錐角。如∑已按要求確定，獨立的設計變量就只有大端端面模數met，小錐齒輪齒數z1，錐齒輪齒寬b，因此設計變量為：

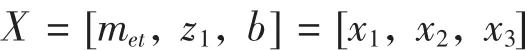
1.2 目標函數

滿足設計條件下，盡量節約材料，以直齒錐齒輪傳動中小、大齒輪體積之和最小為優化目標，考慮錐齒輪實際結構的復雜性，較難用準確的關系式表達，故此采用大端與小端分度圓之間的截頭圓錐體積進行計算[5]，可表達為：

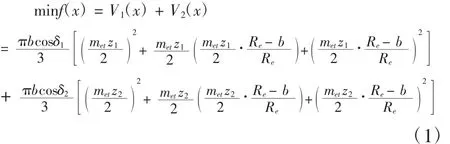
1.3 約束條件

（1）大端端面模數met約束條件

大端端面模數met應符合GB/T12368-1990錐齒輪模數之規定，通常根據設計條件確定范圍[4]，取met=2~10，可得：

式中：tanδ1=z1/z2=1/u，tanδ2=z2/z1=1/u，Re為外錐距，按式（2）計算。

（2）小錐齒輪齒數z1約束條件

小齒輪齒數z1通常取16~30之間[1]，可得：

（3）錐齒輪齒寬b約束條件

齒寬b通常取整數，錐齒輪傳動的齒寬系數ΦR常取1/4~1/3[1]，可得：

（4）齒面接觸疲勞強度條件

根據GB/T10062-2003，應滿足齒面接觸疲勞強度條件[1-2]，可得：

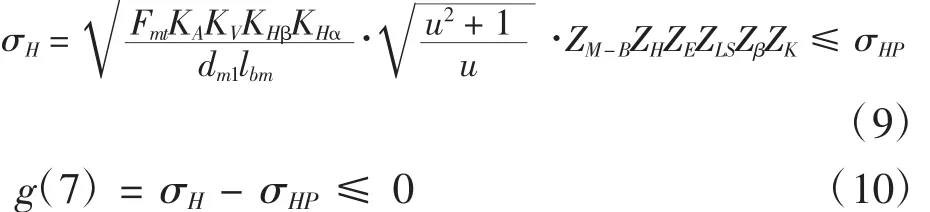
式中：σH為齒面接觸應力（MPa）；σHP為許用齒面接觸應力（MPa）；Fmt為齒寬中點分錐上的名義切向力（N）；KA為使用系數；KV為動載系數；KHβ為接觸強度齒向載荷分布系數；KHα為接觸強度端面載荷分配系數；ZM-B為中點區域系數；ZH為節點區域系數；ZE為彈性系數；ZLS為載荷分擔系數；Zβ為螺旋角系數；ZK為錐齒輪系數；dm1為小錐齒輪中點節圓直徑（mm）；lbm為中點接觸線長度（mm）.根據設計條件，參考國標或文獻[1]和[2]，確定以上各參數數值。

（5）齒根彎曲疲勞強度條件

根據GB/T10062-2003，應滿足齒根彎曲疲勞強度條件[1-2]，可得：

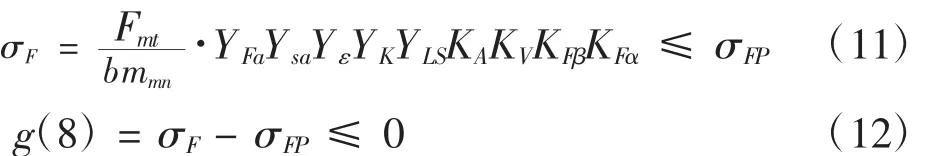
式中：σF為齒根彎曲應力（MPa）；σFP為許用齒根彎曲應力（MPa）；mmn為中點法向模數；YFa為齒形系數；Ysa為應力修正系數；Yε為重合度系數；YK為彎曲強度錐齒輪系數；YLS為彎曲強度載荷分擔系數；KFβ為彎曲強度齒向載荷分布系數；KFα為彎曲強度端面載荷分配系數。根據設計條件，參考國標或文獻[1]和[2]，確定以上各參數數值。

2 設計實例與常規設計結果

設計某傳動用閉式直齒錐齒輪傳動，已知小齒輪傳遞的轉矩為T1=400 N·m，小齒輪轉速n1=960 r/min，齒數比u=z2/z1=3，兩輪軸線相交成90°，設計精度等級為IT6級，長期工作。大小齒輪均采用20Cr，滲碳、淬火，齒面硬度為58~63 HRC，許用齒面接觸應力σHP=1 087 MPa，許用齒根彎曲應力σF=450 MPa[1].

直齒錐齒輪傳動的常規設計步驟為[1]：首先，初選小錐齒輪齒數z1，由齒面強度估算公式計算最小小齒輪大端分度圓直徑de1.然后確定大端端面模數met和齒輪寬度b，計算其它錐齒輪尺寸參數。最后校核齒面接觸疲勞強度和齒根彎曲疲勞強度，如驗算合格則設計可行，如不滿足條件則需調整參數直到滿足強度條件。

根據上述步驟進行設計，可得常規設計結果：大端端面模數met=5.5，小錐齒輪齒數z1=19，大錐齒輪齒數z2=57，外錐距Re=165.229 mm，錐齒輪齒寬b=50 mm，齒寬系數ΦR=0.302 6，小齒輪大端分度圓直徑de1=104.5 mm，大齒輪大端分度圓直徑de2=313.5 mm，其余參數可由相關公式計算得到。

3 優化求解

3.1連續變量求解

將變量按連續值處理，求解后進行圓整和取標準值得出優化方案[3-4]。對于有約束條件的連續變量優化設計問題，求解方法很多，常規算法有隨機方向法、復合形法、可行方向法、懲罰函數法等，還可采用智能算法，如粒子群算法（PSO）、遺傳算法（GA）、模擬退火算法（SA）、蟻群算法（ACO）等[7-8]。Matlab軟件中，對于非線性約束條件的優化問題，提供了fmincon函數進行求解，而不再需要編寫相應的算法程序，使求解更為方便。同時，采用粒子群算法在Matlab軟件中進行編程，對該優化問題進行求解，以對比求解結果。

（1）fmincon函數優化求解

根據前述條件，確定各參數的數值或函數關系式，編寫優化目標函數文件（aim_1.m）和約束條件文件（const_1.m），以常規設計結果為優化求解初始點，調用fmincon函數進行求解，程序如下：

x0=[5.5 19 50]；

A=[]；b=[]；Aeq=[]；beq=[]；

xlb=[2 16 10]；

xub=[10 30 100]；

options=optimset（'Display'，'iter-detailed'，'MaxFunEvals'，2000）；

[x，fval，exitflag，output]=fmincon（'aim_1'，x0，A，b，Aeq，beq，xlb，

xub，'const_1'，options）

運行程序后可以得到如下求解結果：

X1=[4.5214 21.0216 38.4166]

（2）粒子群算法優化求解

將目標函數和約束條件程序輸入到粒子群算法相應程序位置[8]，然后運行粒子群算法程序，可以得到如下求解結果：

X2=[4.5218 21.0240 38.4365]

圖1所示為粒子群算法適應度曲線，可以看到初始迭代過程中目標函數下降很快，隨著迭代次數的增多，目標函數下降平緩，從91次迭代開始，目標值下降微小，基本不變。比較fmincon函數和PSO算法求解結果，兩者相近。根據求解結果，進行取整和取標準值，可得X3=[4.5 21 39]，即大端端面模數met=4.5，小錐齒輪齒數z1=21，齒寬b=39 mm，對于結果的可行性需要校核強度條件。

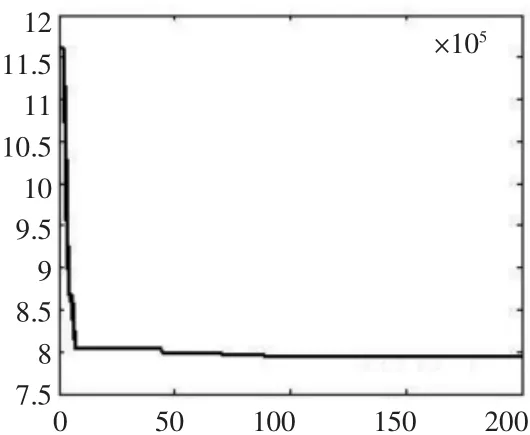
圖1 粒子群算法求解適應度曲線

3.2 離散變量求解

由前面分析可知，大端端面模數met、小齒輪齒數z1、錐齒輪寬度b實際都是離散變量，將其作為離散變量進行優化求解，在使用上更為合理和準確。對于離散變量的優化求解，可采用離散化法、離散復合形法、分支定界法等[9-10]，以上方法需要編寫相應算法程序即可實現。在Lingo軟件中，通過較為簡單的程序語言設定即可將變量離散化處理，而目標函數和約束條件的編寫與Matlab軟件相近，通過設置求解器可較快捷地進行優化求解[11]。

在Lingo軟件中編寫目標函數和約束條件，通過（x1#EQ#3）#OR#（x1#EQ#3.25）#OR#（x1#EQ#3.5）等語句設定大端端面模數met（x1）為標準值，通過@gin（x2）和@gin（x3）語句設定小齒輪齒數z1（x2）和齒寬b（x3）為整數，然后運行程序進行求解，可得如下求解結果：

X4=[4.52140]

將不同求解結果進行比較，如表1所示，可知由連續變量圓整后的解嚴格意義上不滿足強度約束條件，由于接觸應力和彎曲應力與許用值非常接近，在誤差范圍內是可以應用的。由離散求解方法得到的解，滿足強度約束條件，接觸應力和彎曲應力略小于許用值。以大端端面模數met=4.5，小錐齒輪齒數z1=21，齒寬b=40 mm作為優化設計結果，優化后的參數比常規設計在錐齒輪總體積上減小約32%，整體優化效果明顯。

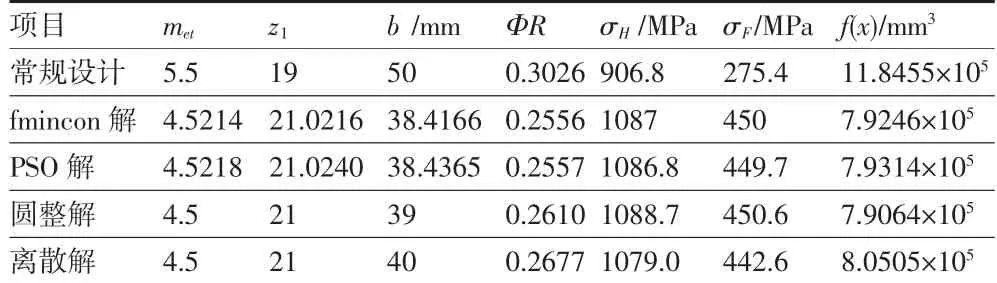
表1 常規設計與優化設計結果

4 結論

將優化設計理論和方法應用于直齒錐齒輪傳動中，以錐齒輪體積之和最小為優化設計目標，分析了邊界約束條件和強度約束條件，結合實例得出常規設計方案，通過程序編寫構建出優化數學模型。通過fmincon函數和粒子群算法在Matlab軟件中進行連續變量求解，分析圓整解可能存在的非可行解等問題，利用Lingo軟件將設計變量離散化，進行優化求解，得到優化設計方案，在滿足約束條件下優化效果顯著。

[1]機械設計手冊編委會.機械設計手冊：第3卷：第16篇[M]. 3版.北京：機械工業出版社，2004：145-186.

[2]朱孝錄.齒輪傳動設計手冊[M].北京：化學工業出版社，2010：264-316.

[3]黃乾貴，張艷.基于遺傳算法的弧齒錐齒輪傳動的優化設計[J].機械傳動，2003，27（4）：32-33.

[4]李鐵軍，朱成實，葉龍.基于遺傳算法的可控螺旋角錐齒輪傳動的優化設計[J].機械傳動，2007，31（2）：42-44.

[5]程進.基于枚舉法的錐齒輪傳動優化設計[J].西昌學院學報（自然科學版），2009，23（1）：44-46.

[6]徐志楊，李艾民，張傳輝，等.基于混合離散變量復合形法的弧齒錐齒輪優化設計[J].北京聯合大學大學學報（自然科學版），2011，25（3）：34-37.

[7]孫靖民，梁迎春.機械優化設計[M].北京：機械工業出版社，2012：138-165.

[8]高飛.MATLAB智能算法超級學習手冊[M].北京：人民郵電出版社，2014：224-416.

[9]陳立周，俞必強.機械優化設計方法[M].北京：冶金工業出版社，2014：217-236.

[10]張幼軍，玉榮.行星齒輪減速器的優化設計[J].組合機床與自動化加工技術，2008，（10）：19-22.

[11]謝金星，薛毅.優化建模與LINDO/LINGO軟件[M].北京：清華大學出版社，2005：79-131.

The Optimal Design of Straight Bevel Gear Drive based on MATLAB and LINGO

WANG Qin－jun，WU Zhi－guang
（Department of Mechanical Engineering，Shanxi Institute of Mechanical and Electrical Engineering，Changzhi Shanxi 046011，China）

Taking the straight bevel gear drive as the research model，selected the gear's large end module，the tooth number of small bevel gear，and the gear width as design variable，regarded minimal gear volume as optimization goal，the optimal design model is established by setting gear strength and other constraint conditions. Combined with design example，the traditional design scheme is obtained.The optimal solution of continuous variable is obtained through Matlab，and the optimal solution of discrete variable is obtained through Lingo.Then the optimization scheme is obtained by comprehensive analysis of the solutions.Compared with the traditional design scheme，the gear volume is reduced by 32%，so the effect of optimization is significant，can provide the necessary reference for design.

straight bevel gear drive；optimal design；continuous variable；discrete variable

TH132.41

A

1672-545X（2017）06-0030-04

2017-03-09

王沁軍（1982-），男，山西晉城人，碩士，研究方向為計算機輔助設計與制造。