基于后驗風險的多源先驗信息融合方法
陳洪科
(廈門大學嘉庚學院,福建漳州363105)
基于后驗風險的多源先驗信息融合方法
陳洪科
(廈門大學嘉庚學院,福建漳州363105)
針對多源先驗信息Bayes融合中先驗分布權重分配問題,提出了一種基于后驗風險的權重確定方法——構造后驗風險矩陣,并基于后驗風險與先驗分布權重成反比的原則建立權重求解方程進而求得各先驗分布的權重系數。通過算例證明了該方法的有效性。
多源信息融合;后驗風險;Bayes;可靠性
Bayes方法在產品的小子樣可靠性評定中得到了非常廣泛的應用。該方法的顯著特色與優點在于能夠利用產品先驗信息,例如工程實踐中長期積累的經驗、專家意見以及歷史可靠性信息等。然而,其優點也是實際應用的難點所在,如何有效地融合多種驗前信息,從而得到合理的綜合先驗分布進行統計推斷,是一個受到普遍重視問題。
多源先驗信息融合的關鍵在于確定不同先驗分布在綜合先驗分布中的合理權重。典型方法包括由專家確定各先驗分布在融合中的權重、由各先驗信息可信度確定權重[1-2]、自助融合估計法(Bootstrap方法或隨機加權方法)[3]。這些方法具有良好的工程應用價值,但也存在不足之處:專家確定權重難以保證精度,主觀性較大[4];先驗信息可信度的確定在某些情況下比較困難,適用范圍有限;自助融合估計方法以先驗信息的可信度為基礎,不僅存在可信度難以確定的問題,而且通過直方圖確定先驗分布的做法受主觀因素干擾。近年來,針對這些方法的應用改進持續進行,同時也出現了基于D-S證據理論、第2類極大似然估計原理(ML-II)、分布圖、概率模型等的新方法[5-8]。本文基于Bayes統計理論中“后驗風險”概念提出了一種多源先驗信息融合方法,下面給出具體論述。
1 多源先驗信息的Bayes融合
假設某產品壽命服從參數為θ的分布,其密度函數記為f(t|θ)。為了評估該產品的可靠性水平,現抽取n個樣本進行現場試驗。一般得到的試驗數據為截尾數據,不妨記為X,其中r個樣本失效,失效時間序列為t1≤t2≤…≤tr,其余的n-r個在時間ts截尾(定數截尾時,ts=tr;定時截尾時,ts即定時時間)。
如果現場試驗之前已獲取了m源先驗信息,經轉化得到m個先驗分布πi(θ)(i=1,2,…,m)。假設已知每個先驗分布的權重,記作w=(wi)1×m,其中wi即是分布πi(θ)的權值且所有權值之和為1。那么融合各先驗分布得到的綜合先驗

由上述數據模型可得似然函數
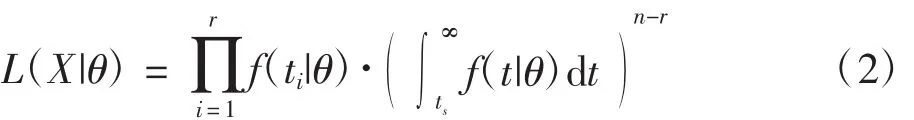
而先驗分布πi(θ)下的后驗分布則是根據Bayes定理,融合后驗分布
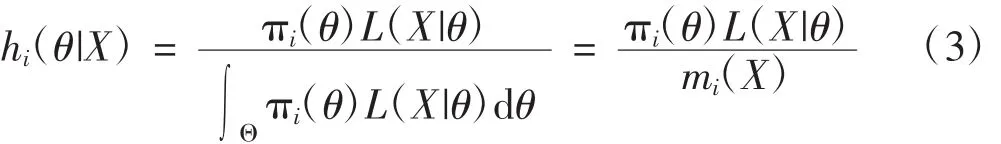
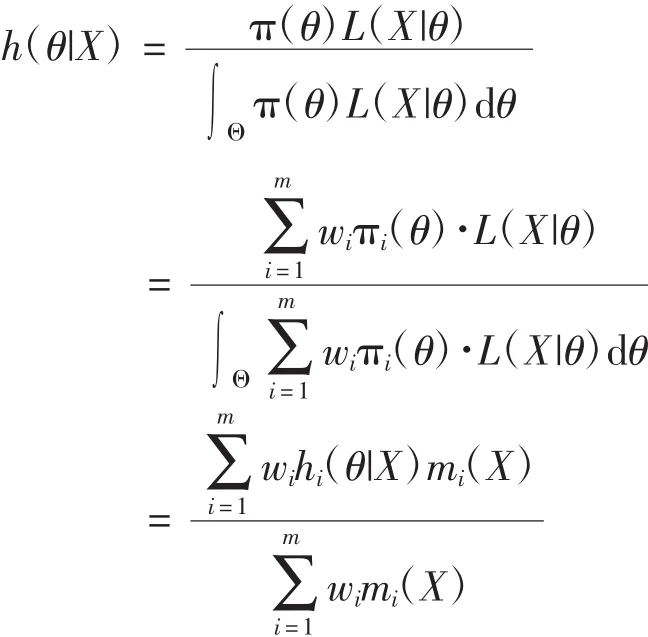
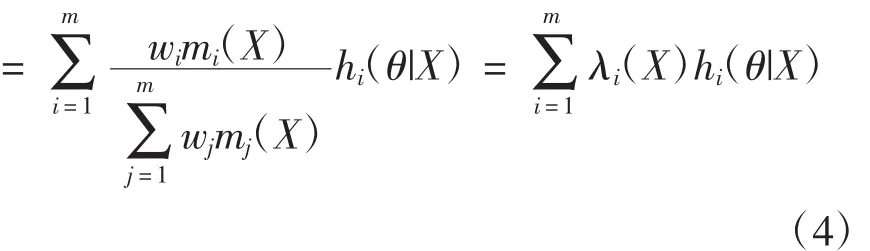
(4)式的計算結果表明,融合后驗分布是不同先驗信息源下后驗分布的加權和。在平方差損失函數下,參數θ的融合后驗估計
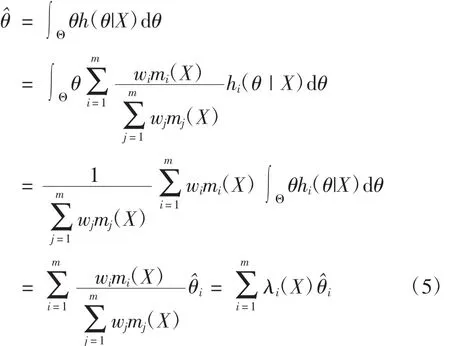
(5)式的計算結果表明,融合后驗估計也是不同先驗信息源下后驗估計的加權和。顯然,利用這種融合后驗分布進行Bayes統計決策分析是比較便利的。
2 權值計算
Bayes決策分析中常用“后驗風險”作為評定估計量的好壞的標準[9]。一般地,如果參數先驗分布越接近真實分布,那么由Bayes定理計算得到的參數估計便越接近真實值。直觀地想,不同先驗分布的精確度不同,利用它所得的參數估計的精度也不同。在相同的損失函數下,參數估計越精確,采納該估計所承擔的風險也就越小,該先驗分布的權重也就越高。因此,可以用后驗風險來衡量權值的大小。當然,為了能夠比較,還需對其作一些擴展。
假設計算中采用平方差損失函數

對于任一先驗分布πi(θ),由它算得的參數估計值
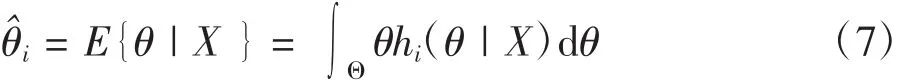
根據文獻[9],此估計量對現場數據X的后驗風險
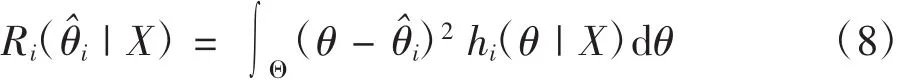
為了能縱向地比較不同先驗分布下所得參數估計的后驗風險,將(8)式修改為

當i=j時,Rij就是一般意義上的后驗風險。不妨記

稱之為后驗風險矩陣。(9)式與(8)式的主要不同在于利用融合后驗分布h(θ|X)而非hj(θ|X)來計算后驗風險。這樣做既能提高后驗風險的計算精確度,又為不同先驗分下布后驗風險的比較提供了一個基準。
依前所述,先驗分布后驗風險越小,其權值越大;反之,其權值越小,因此后驗風險的比值與權值的比值成反比,即有
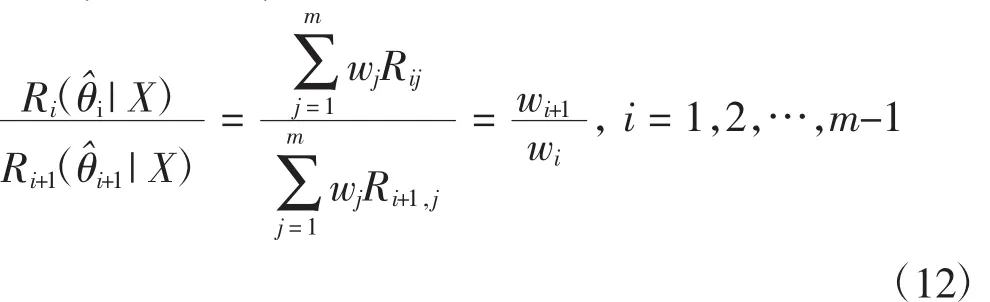
進一步整理(12)式,再結合

得到由m個方程構成的方程組

這是一個非線性方程組,m=2時可直接求解,m≥3時則需運用數值方法(如牛頓迭代法)[10]解出m個權值。
3 數值例
某產品壽命服從正態分布N(θ,1),其中θ為未知參數,并設其真值為10.假定現場抽取8個產品進行定數截尾試驗,當失效樣本數達到5個時停止試驗。從分布N(10,1)中抽取隨機數模擬現場試驗,得到數據X:8.283 7、9.441 8、9.908 7、10.032 2、10.156 4、10.156 4、10.156 4、10.156 4.現場試驗之前已獲取兩個先驗信息,經轉化得到兩個先驗分布,分別是
π1(θ)=N(9,1)
π2(θ)=N(12,1)
結合現場數據,在平方損失下,由它們算得的θ估計值依次為9.945 1、10.325 0.計算出后驗風險矩陣為
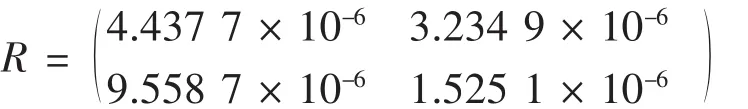
列方程組解得權值
w1=0.620 8,w2=0.379 2
再計算出
m1(X)=3.552 6×10-5,m2(X)=1.185 0×10-5
根據(5)式求得融合后驗估計
θ贊=10.009 4
與單個先驗分布下的估計結果相比,融合后驗估計更加接近參數θ的真實值10.
4 結束語
先驗信息融合是Bayes理論應用于產品小子樣統計評定中的關鍵環節,也是Bayes理論和可靠性統計領域的持續研究熱點。本文針對信息融合過程中的先驗分布權重分配問題,提出通過構造后驗風險矩陣并基于后驗風險與先驗分布權重成反比的原則建立起權重求解方程并求得各分布的融合權重,算例驗證證實了方法的有效性,為該問題的解決提供了一種新的思路。
[1]張士峰.多源驗前信息的融合方法[J].飛行器測控學報,2000,19(1):26-30.
[2]張金槐.多源信息的Bayes融合精度鑒定方法[J].國防科技大學學報,2001,23(3):93-97.
[3]張金槐.多種驗前信息源情況下的融合驗后分布[J].飛行器測控技術,1998,17(3):28-35.
[4]柴建,師義民,李秀春,等.多源驗前信息下的Bayes信息融合方法[J].數理統計與管理,2007,27(3):308-311.
[5]毛昭勇,宋保維,胡海豹,等.基于分布圖信息融合的Bayes可靠性評定方法[J].火力與指揮控制,2010,35(7):90-93.
[6]劉本紀,龔時雨.Bayesian可靠性評估中多源信息融合的概率模型方法[J].電子產品可靠性與環境試驗,2011,29(1):10-13
[7]侯敏,郭基聯,李建偉.多源信息的驗前分布融合方法研究[J].火力與指揮控制,2012,37(7):57-60.
[8]趙仿澤.一種基于D-S證據理論的Bayes可靠性評定方法[J].魚雷技術,2013,21(3):175-178.
[9]張堯庭,陳漢峰.貝葉斯統計推斷[M].北京:科學出版社,1991.
[10]徐萃薇,孫繩武.計算方法引論[M].北京:高等教育出版社,2002.
Fusion Method for Prior Distributions from Multiple Sources Based on Posterior Risk
CHEN Hong-ke
(Xiamen University Tan Kah Kee College,Zhangzhou Fujian 363105,China)
In order to assign justified weight coefficients for prior distributions from multiple sources in Bayes analysis,a method was proposed based on posterior risk.Posterior risk matrix was constructed in this method and then equations for weight coefficients were established based on the principle that weight of prior distribution being inversely proportional to posterior risk.The given numerical example verified the validity of this method.
information fusion from multiple sources;posterior risk;Bayes;reliability
TB114.3
A
1672-545X(2017)06-0223-03
2017-03-09
陳洪科(1986-),男,講師,碩士,主要從事產品可靠性、嵌入式系統研究。

