代數(shù)推理，一項需要長期培養(yǎng)的能力

張海強

代數(shù)推理，一項需要長期培養(yǎng)的能力

張海強

代數(shù)推理；基本工具；基本技能；基本程序；代數(shù)思維

縱觀2017年江蘇高考試卷，試題分為容易題、中檔題、難題三個層次。其中填空題的14題，解答題的19題和20題均可歸為“難題”層次，而這三題均以代數(shù)推理為底色，著重檢測學生抽象思維能力的層次。筆者試圖結合高考試題就如何提升學生的代數(shù)推理能力提幾點建議。

1.幫助學生完善代數(shù)推理的基本工具。

《普通高等學校招生全國統(tǒng)一考試考試大綱》指出：推理是思維的基本形式之一，它由前提和結論兩部分組成，推理既包括演繹推理，也包括合情推理。

高中代數(shù)知識與方法涉及集合、邏輯知識、函數(shù)、數(shù)列、解析幾何、概率統(tǒng)計等眾多分支，但就代數(shù)的歷史發(fā)展而言，方程與函數(shù)應成為高中代數(shù)的核心。因此要仔細研究方程與函數(shù)中的思想與方法，使之成為我們代數(shù)推理的“工具包”。例如填空題第14題以方程解的個數(shù)為背景，通過轉化化歸為函數(shù)問題，滲透數(shù)形結合的思想，既直觀又精細；推理方法既包含直接推理，也包含間接推理，對學生的代數(shù)推理提出了較高的要求。

2.幫助學生擁有代數(shù)推理的基本技能。

代數(shù)作為概括和抽象的算術，體現(xiàn)了具體與抽象的關系，因此具體化應成為代數(shù)推理的一項基本技能；代數(shù)推理既包括演繹推理，也包括合情推理，因此特殊化和一般化也應成為代數(shù)推理的一項基本技能；高中代數(shù)知識豐富，涉及面廣，這就為代數(shù)推理提供了多彩的模型（如等差數(shù)列模型、函數(shù)模型等），因此模型化也應成為代數(shù)推理的基本技能。如此種種，不一而足。

例如解答題19題，等差數(shù)列理所當然成為本題的一個思維模型，由等差數(shù)列的等距性可知：當 n≥4 時，an-3+an+3=2an，an-2+an+2=2an，an-1+an+1=2an，

以上三式相加即可證得第1小問。

對于第2小問：當n≥4時，

由{an}是“P⑶數(shù)列”知，

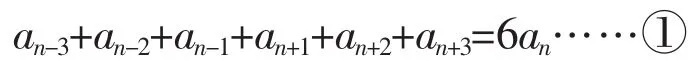
當 n≥3 時，由{an}是“P⑵數(shù)列”知，

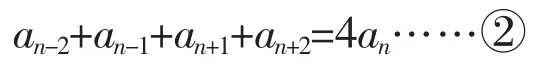
至此學生陷入困境。究其原因是因為無法理解這兩個符號化的數(shù)學等式。

如果將①②具體化和特殊化，則可以得到如下等式：

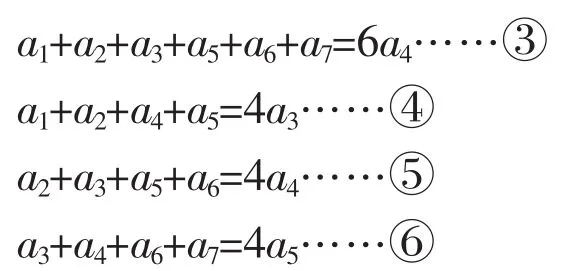
由③④⑥知：2a4=a3+a5，將這一過程一般化可覓得證明思路。

3.幫助學生構建處理代數(shù)推理題的基本程序。

為便于學生操作，教師在教學中宜和學生一起構建處理代數(shù)推理題的基本程序。例如解答題20題，第一個不可回避的環(huán)節(jié)就是弄懂情景，領悟試題的數(shù)學本質。為此宜列出條件和結論的清單，留意細節(jié)，特別關注文字和符號的表述與轉換。如第1小問就需要將條件①f（x）有極值和條件②導函數(shù) f′（x）的極值點是 f（x）的零點進行轉譯。

第二環(huán)節(jié)是明確目標，即在審題的基礎上，利用代數(shù)推理的工具將題設與結論的信息進行提取、轉化、加工和傳輸，從而明確解題的目標與方向。如第2小問通過轉化后即可把問題轉化為：若（a∈（3，+∞）），則 b2＞3a。

第三個環(huán)節(jié)是推理論證，利用代數(shù)推理的基本技能對試題進行論證或求解，并用恰當?shù)恼Z言加以表述。第2小問的證明充分展示了分析法與綜合法的結合。

由此可知處理代數(shù)推理題的基本程序：弄通情景—明確目標—推理論證。

代數(shù)推理是一項需要長期培養(yǎng)的能力，既需要教師潛移默化的引導和滲透，更需要學生以孜孜以求的精神去領悟與踐行。代數(shù)推理既以代數(shù)思維為基礎，又是理解代數(shù)思維的重要手段，而等價、比較、變量、模式、關系，函數(shù)、方程和不等式是高中代數(shù)思維的核心思想，這就為高中代數(shù)推理教學提供了一個大致的框架。

［1］曹一鳴，王竹婷.數(shù)學“核心思想”代數(shù)思維教學研究［J］.數(shù)學教育學報，2007（01）.

［2］何繼剛.例說代數(shù)推理的認知因素和教學建議——對一道試題的教學反思［J］.數(shù)學通訊，2011（05）.

［3］華志遠.走出代數(shù)推理教學的困境［J］.中學數(shù)學教學參考，2000（04）.

［4］吳寶瑩.代數(shù)推理問題的思維方略［J］.中學數(shù)學月刊，2015（01）.

G633.6

A

1005-6009（2017）51-0059-01

張海強，江蘇省宜興中學（江蘇宜興，214200）教師，高級教師，江蘇省特級教師。